线性代数部分—矩阵理论
一、矩阵基本概念
1、矩阵的定义—形如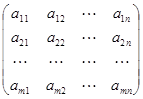 ,称为矩阵
,称为矩阵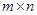 ,记为
,记为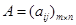 。
。
特殊矩阵有
(1)零矩阵—所有元素皆为零的矩阵称为零矩阵。
(2)方阵—行数和列数都相等的矩阵称为方阵。
(3)单位矩阵—主对角线上元素皆为1其余元素皆为零的矩阵称为单位矩阵。
(4)对称矩阵—元素关于主对角线成轴对称的矩阵称为对称矩阵。
2、同型矩阵—行数和列数相同的矩阵称为同型矩阵。若两个矩阵同型且对应元素相同,称两个矩阵相等。
3、矩阵运算
(1)矩阵加、减法:
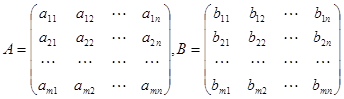 ,则
,则
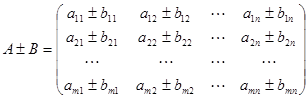 。
。
(2)数与矩阵之积:
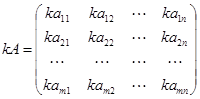 。
。
(3)矩阵与矩阵之积:
设 ,则
,则
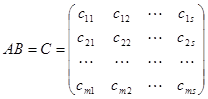 ,
,
其中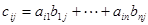 (
(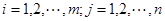 )
)
【注解】
(1)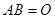 不一定有
不一定有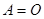 或
或 。
。
(2)矩阵乘法没有交换律。
(3)含方阵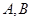 的矩阵多项式可象普通多项式一样因式分解的充分必要条件是
的矩阵多项式可象普通多项式一样因式分解的充分必要条件是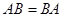 。
。
(4)设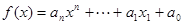 ,则定义
,则定义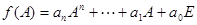 ,且关于矩阵
,且关于矩阵 的矩阵多项式可因式分解。
的矩阵多项式可因式分解。
二、方程组的矩阵形式及解的概况
方程组的基本形式为
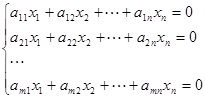 (1)
(1)
称(1)为齐次线性方程组。
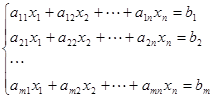 (2)
(2)
称(2)为非齐线性方程组。
令 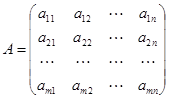 ,
, ,
, ,则(1)、(2)可分别表示为矩阵形式:
,则(1)、(2)可分别表示为矩阵形式:
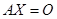 (1)
(1)
…… …… 余下全文

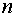 阶两种类型;主要方法是应用行列式的性质及按行\列展开定理化为上下三角行列式求解。
阶两种类型;主要方法是应用行列式的性质及按行\列展开定理化为上下三角行列式求解。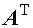 、
、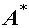 、
、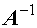 等的相关性质,及性质
等的相关性质,及性质 (其中
(其中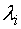 为矩阵
为矩阵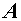 的特征值)。
的特征值)。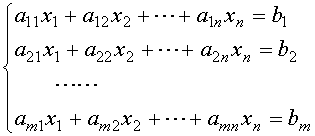
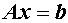 ,其中
,其中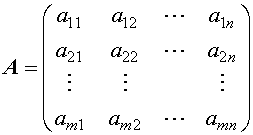 ,
,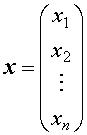 ,
,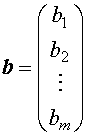
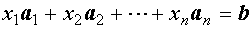 ,其中
,其中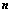 行列式共有
行列式共有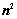 个元素,展开后有
个元素,展开后有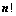 项,可分解为
项,可分解为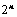 行列式;
行列式;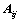 和
和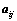 的大小无关;
的大小无关;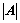 ;
;
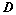 :
: ,则
,则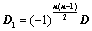 ;
;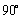 ,所得行列式为
,所得行列式为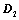 ,则
,则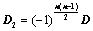 ;
;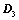 ,则
,则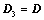 ;
;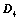 ,则
,则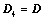 ;
;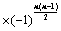 ;
;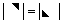 ):主对角元素的乘积;
):主对角元素的乘积;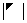 和
和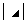 :副对角元素的乘积
:副对角元素的乘积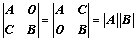 、
、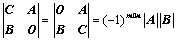
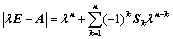 ,其中
,其中 为
为 阶主子式;
阶主子式; 的方法:
的方法: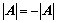 ;
;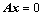 ,证明其有非零解;
,证明其有非零解;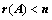 ;
;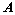 是
是