《线性代数》复习提纲
第一章、行列式
1.行列式的定义:用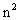 个元素
个元素 组成的记号称为n阶行列式。
组成的记号称为n阶行列式。
(1)它表示所有可能的取自不同行不同列的n个元素乘积的代数和;
(2)展开式共有n!项,其中符号正负各半;
2.行列式的计算
一阶|α|=α行列式,二、三阶行列式有对角线法则;
N阶(n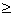 3)行列式的计算:降阶法
3)行列式的计算:降阶法
定理:n阶行列式的值等于它的任意一行(列)的各元素与其对应的代数余子式乘积的和。
方法:选取比较简单的一行(列),保保留一个非零元素,其余元素化为0,利用定理展开降阶。
特殊情况:上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积;
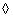 行列式值为0的几种情况:
行列式值为0的几种情况:
Ⅰ 行列式某行(列)元素全为0; Ⅱ 行列式某行(列)的对应元素相同;
Ⅲ 行列式某行(列)的元素对应成比例; Ⅳ 奇数阶的反对称行列式。
3.概念:全排列、排列的逆序数、奇排列、偶排列、余子式 、代数余子式
、代数余子式
定理:一个排列中任意两个元素对换,改变排列的奇偶性。
奇排列变为标准排列的对换次数为基数,偶排列为偶数。
n阶行列式也可定义: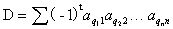 ,t为
,t为 的逆序数
的逆序数
4.行列式性质:
1、行列式与其转置行列式相等。
2、互换行列式两行或两列,行列式变号。若有两行(列)相等或成比例,则为行列式0。
…… …… 余下全文

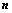 行列式共有
行列式共有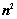 个元素,展开后有
个元素,展开后有 项,可分解为
项,可分解为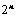 行列式;
行列式;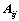 和
和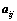 的大小无关;
的大小无关;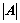 ;
;
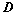 :
: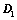 ,则
,则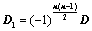 ;
;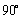 ,所得行列式为
,所得行列式为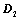 ,则
,则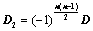 ;
;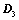 ,则
,则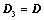 ;
;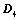 ,则
,则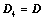 ;
;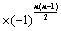 ;
;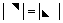 ):主对角元素的乘积;
):主对角元素的乘积; 和
和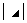 :副对角元素的乘积
:副对角元素的乘积 、
、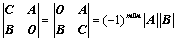
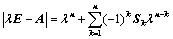 ,其中
,其中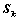 为
为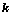 阶主子式;
阶主子式;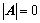 的方法:
的方法: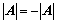 ;
;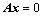 ,证明其有非零解;
,证明其有非零解;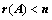 ;
;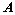 是
是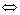
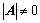 (是非奇异矩阵);
(是非奇异矩阵);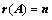 (是满秩矩阵)
(是满秩矩阵)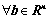 ,
, 总有唯一解;
总有唯一解;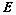 等价;
等价;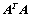 是正定矩阵;
是正定矩阵;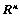 的一组基;
的一组基;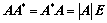 无条件恒成立;
无条件恒成立;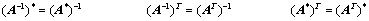
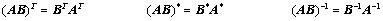
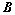 可逆:
可逆: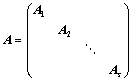 ,则:
,则: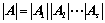 ;
;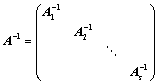 ;
;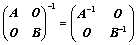 ;(主对角分块)
;(主对角分块)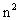 个元素
个元素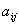 组成的记号称为n阶行列式。
组成的记号称为n阶行列式。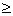 3)行列式的计算:降阶法
3)行列式的计算:降阶法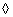 行列式值为0的几种情况:
行列式值为0的几种情况: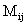 、代数余子式
、代数余子式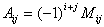
 ,t为
,t为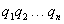 的逆序数
的逆序数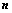 行列式共有
行列式共有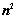 个元素,展开后有
个元素,展开后有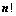 项,可分解为
项,可分解为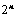 行列式;
行列式; 和
和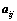 的大小无关;
的大小无关;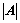 ;
;
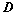 :
: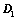 ,则
,则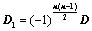 ;
;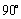 ,所得行列式为
,所得行列式为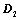 ,则
,则 ;
;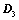 ,则
,则 ;
;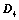 ,则
,则 ;
;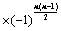 ;
;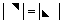 ):主对角元素的乘积;
):主对角元素的乘积;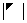 和
和 :副对角元素的乘积
:副对角元素的乘积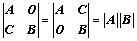 、
、
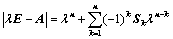 ,其中
,其中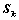 为
为 阶主子式;
阶主子式;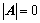 的方法:
的方法: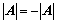 ;
;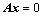 ,证明其有非零解;
,证明其有非零解;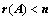 ;
;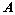 是
是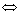
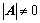 (是非奇异矩阵);
(是非奇异矩阵);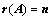 (是满秩矩阵)
(是满秩矩阵)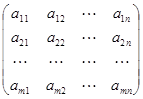 ,称为矩阵
,称为矩阵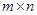 ,记为
,记为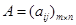 。
。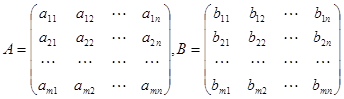 ,则
,则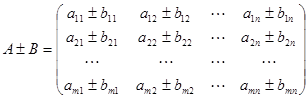 。
。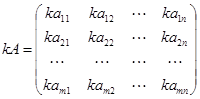 。
。 ,则
,则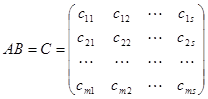 ,
,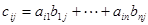 (
(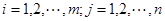 )
)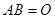 不一定有
不一定有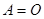 或
或 。
。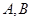 的矩阵多项式可象普通多项式一样因式分解的充分必要条件是
的矩阵多项式可象普通多项式一样因式分解的充分必要条件是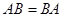 。
。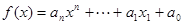 ,则定义
,则定义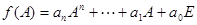 ,且关于矩阵
,且关于矩阵 的矩阵多项式可因式分解。
的矩阵多项式可因式分解。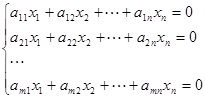 (1)
(1)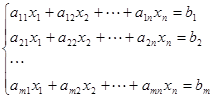 (2)
(2)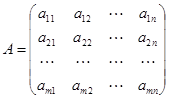 ,
, ,
, ,则(1)、(2)可分别表示为矩阵形式:
,则(1)、(2)可分别表示为矩阵形式: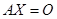 (1)
(1)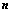 行列式共有
行列式共有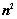 个元素,展开后有
个元素,展开后有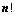 项,可分解为
项,可分解为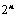 行列式;
行列式; 和
和 的大小无关;
的大小无关;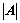 ;
;
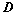 :
: ,则
,则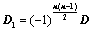 ;
;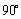 ,所得行列式为
,所得行列式为 ,则
,则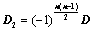 ;
;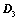 ,则
,则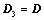 ;
;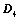 ,则
,则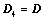 ;
;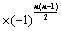 ;
;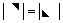 ):主对角元素的乘积;
):主对角元素的乘积; 和
和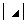 :副对角元素的乘积
:副对角元素的乘积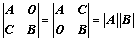 、
、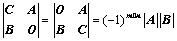
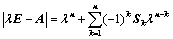 ,其中
,其中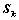 为
为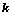 阶主子式;
阶主子式;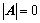 的方法:
的方法: ;
;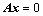 ,证明其有非零解;
,证明其有非零解;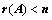 ;
; 是
是