第十一课时
教学内容：教科书第199—201页例7，完成相应的练习题和习题3。5第1—4题。
教学目的：继续学习用一元一次方程解应用题。
教学过程：
一、复习
1、完成第199页第13、15题。
2、集体小结。
二、新授
1、教学例1
出示例1
在甲处劳动的有27人，在乙处劳动的有19人。现在另调20人去支援，使在甲处的人数为在乙处的人数的2倍，应调往甲乙两处的各多少人？
分析：在甲乙两处劳动的分别是27人、19人，现在调20人去支援，调往甲、乙两处是未知数，如设调往甲处为X人，则调往乙处为（20-X）人，再根据本题题意找出相等关系：
调入后甲处人数=2×调入后乙处人数
解：设应该调往甲处X人，那么调往乙处的人数就是20-X。于是调入以后甲处有（27+X）人，乙处有[19+（20-X）]人。根据题意列方程，得
27+X=2[19+（20-X）]
解得这个方程得X=17
20-17=3（人）
师指出：本题虽要求出两个未知数的值，但由于这两个未知灵敏的和是20，所以只要用字母X表示其中的一个未知数，就可以用代数式20-X表示另一个未知数。
三、课堂练习
完成第201页第1、2题。
四、总结（略）
五、作业
完成习题3。4（2）第1、2题。
教后记：本节课是方程应用题中的劳动分配问题，这道例题和前面接触的例题和习题的不同之处除了内容本身之外，还从问一个未知数发展到问两个未知数，并且这两个未知数必须在列方程时一并考虑到。这就要求学生能够运用以前所学生用代数式表示未知数量的知识来解这类题。基本上这个例题的教学中学生在理解上并没出现在障碍。
第十二课时
教学内容：教科书第202页例8，完成相应的练习题和习题3。4（2）第3、4题。
教学目的：学习用一元一次方程解答工程应用题。
教学过程：
一、复习
1、完成第201页练习题。
2、集体小结。
二、新授
1、教学例8
出示例8
一件工作，甲单独做要20小时完成，乙单独做12小时完成。现在先由甲单独做4小时，剩下的部分由甲、乙合做。剩下的部分需要几小时完成？
分析：这个问题里的相等关系可以表示为
全部工作量=甲单独做的工作量+甲、乙合做的工作量
我们知道：工作量=工作效率×工作时间
这里的工作效率是用分数表示的：一件工作需要a小时完成，那么1小时的工作效率为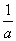
。
即在工程问题中，可以把全部工作量看作1。这样，我们用含有未知数的代数式表示甲单独做工作量以及甲、乙合做工作量后，就可找出等量关系列出方程。
解：设剩下的部分由甲、乙合做需要X小时，根据题意列方程，得
+
+
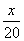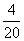=1
解得这个方程得X=6
师指出：教科书中的图中，整个圆表示全部工作题1，无斜线部分表示两人合做前甲已完成的工作量。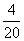
三、课堂练习
完成第204页练习题。
四、总结（略）
五、作业
完成习题3。4（2）第3--8题。
第十三课时
教学内容：教科书第204—206页例9，完成相应的练习题和习题3。4（2）中的第9—11题。
教学目的：学习用一元一次方程解浓度配比问题类的应用题。
教学过程：
一、复习
1、完成第204页练习题。
2、指名学生完成，集体小结。
二、新授
1、导入
师出示教科书第204页两个问题：（见教科书）
师指出：问题（1）中“含盐18%的盐水”，是指1千克这样的盐水中，含纯盐1……18%千克，即0。18千克，所以a千克这样的盐水中，含纯盐0。18a千克。
问题（2）中“浓度为75%的酒精溶液”是指1克这样的酒精溶液中，含纯酒精0。75克，所以x克这样的酒精溶液中，含纯酒精0。75x克，含水（x-0。75x）克。
2、教学例9
出示例9
要把30克含盐16%的盐水稀释成含盐0。15%的盐水，需要加水多少克？
分析：盐水加上水后，重量变了，浓度变了，但盐水中的所含的盐的重量没有变。也就是说，这道题中含有这样一个相等关系：
加水前含盐的重量=加水后含盐的重量。
师引导学生列出方程：30×16%=（30+a）×0。15%
指名学生解出方程。
三、课堂练习
完成第206页练习题。
四、总结（略）
五、作业
完成习题3。4（2）第9、11题。
第十四课时
教学内容：教科书第206—207页例10，完成相应的练习题和习题3。4（2）第12—16题。
教学目的：继续学习用一元一次方程解间接未知数的应用题。
教学过程：
一、复习
1、完成第206页练习题。
2、指名学生完成，集体小结。
二、新授
1、教学例10
出示例10
一个两位数，十位上的数比个位上的数小1，十位与个位上的数的和是这个两位数的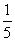
，求这个两位数。
分析：如果直接设所求的两位数为X，那么列方程比较困难。可以把这个求两位数转化为分别求出它的个、十位上的数。也就是说，可能用设间接未知数的方法来解。在本题中，可以先设十位上的数为x，那么个位上的数就是x+1，这个两位数应该是10x+（x+1）。本题的相等关系是
十位上的数+个位上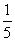数=……两位数
师引导学生列出方程
x+（x+1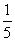）=[10x+（x+1）]
指名学生解出方程。
三、课堂练习
1、完成第207—208页练习题。
2、集体小结。
四、总结（略）
五、作业
完成习题3。4（2）第12—15题。
第二篇：九年级数学教案2。4第二单元第2小节第四、五、课时
第六课时
教学内容：教科书第124页—125页，合并同类项，完成相应的练习题和习
题2.4第1—3题。
教学目的：使学生理解同类项的概念。会判断给出的项是不是同类项。 教学重点：理解同类项的概念。
教学过程：
一、复习提问
什么叫多项式？（几个单项式的和叫做多项式）
新授
1、师出示： 3x+5x -3x2y+5x2y
提问：在第一个多项式中，含有什么字母？字母的次数是多少？在第二个多项式中呢？
指名学生回答后，师指出：在第一个多项式中，5x、3x都含有x，指数都是1。在第二个多项式中，两个项都含有x2y，并且x 的次数是二次，y的次数是一次。
像这样的项：所含字母相同，并且相同字母的次数也要相同的项叫做同类项。几个常数项也是同类项。
2、教学例1（见教科书第125页例1）
师强调同类项必须符合两个条件，一是所含字母相同，二是相同字母的次数也分别相同。这两个条件缺一不可。解题是，可在同类项下面画记号。相同标记的是同类项。
3、教学例2（见教科书第125页例2）
本例可先请一个学生板演，然后集体订正。订正时时应该重点指出，-3xy
与7都没有同类项。
提醒学生注意：熟练以后，同类项下面一般不标记号。
三、课堂练习
完成第125页练习题第1—3题。
四、总结（略）
同类项
五、作业
完成习题2.4第1—3题。
第五课时
教学内容：教科书第126页—127页合并同类项例3、例4，完成相应的练
习题和习题2.4第3—5题。
教学目的：使学生能够运用同类项的概念合并同类项。
教学重点：合并同类项
教学过程：
一、复习
指出下列各题中的两项是不是同类项？
0．2x2y与0.2xy2 4abc与4ac -x2y与y2x
二、新授
我们知道，5x与3x是同类项；-4x2y与3x2y也是同类项。在多项式中遇到同类项，我们可以运用交换律、结合律、分配律将同类项合并。 如：
4x2+2y-3xy+7+3y-8x2
=（4x2-8x2）+ 2y+3y –3xy+7
=（4-8）x2+（2+3）y - 3xy+7
= -4x2+5y-3xy+7
把多项式中的同类项合并成一项，叫做合并同类项。
合并同类项的法则是：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。
2、教学例3（见教科书第127页例3）
本例是合并同类项最基本的题目。可以师生共同完成，在师的引导下学生主动完成。第（2）题在合并的同时，提醒学生注意符号。
3、教学例4（见教科书第128页例4）
本例的项数较多，教学时，除让学生注意遇到类似时不能把项漏掉外，主要的是本题有两点要指出：一是在多项式中，如果两个同类项的系数互为相反数，合并同类项后这两项就相互抵消，结果为0。二是当结果中没有同类项是，就是最后的结果了。
三、课堂练习
完成第128页练习题
四、总结（略）
合并同类项
五、作业
完成习题2.4第3—5题。
第六课时
教学内容：教科书第129页—131页例5、例6，完成相应的练习题和习题
2.4第6-8题。
教学目的：使学生能够熟练运用合并同类项来代入数值。
教学过程：
一、复习
合并下列各多项式的同类项：
-2x3+3x2+2x3-3x2+x-1
x2y-3xy2+2yx2-y2x
二、新授
1、教学例5（见教科书第129页例5）
在解题前师先指出：
当多项式含有同类项时，先把同类项合并，再代入数值进行计算比较简便。
师可以先让一名学生不先合并，直接把数值代入，另一名学生先合并同类项后再代入。看看哪种方法最简便。
很明显，先合并同类项后再代入最简便。
解题中，例5合并同类项后，把原来的二次六项式化成了一次二项式。
2、教学例6（见教科书第131页例6）
指名学生独立完成。集体小结。
三、课堂练习
完成第131页练习题。
四、总结（略）
五、作业
完成习题2.4第6—8题。
教后记：合并同类项是整式加减运算中的重要步骤，在此之前的同类项教学是关键，学生对同类项的理解比较透彻，因此合并同类项的教学很顺利，从练习上看也能说明学生掌握得很好。