高考数学归纳法总结
类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应用的一种主要思想方法.
[例1]试证明:不论正数a、b、c是等差数列还是等比数列,当n>1,n∈N*且a、b、c互不相等时,均有:an+cn>2bn知识依托:等差数列、等比数列的性质及数学归纳法证明不等式的一般步骤.
错解分析:应分别证明不等式对等比数列或等差数列均成立,不应只证明一种情况.
技巧与方法:本题中使用到结论:(ak-ck)(a-c)>0恒成立(a、b、c为正数),从而ak+1+ck+1>ak·c+ck·a.
证明:(1)设a、b、c为等比数列,a= ,c=bq(q>0且q≠1)
,c=bq(q>0且q≠1)
∴an+cn= +bnqn=bn(
+bnqn=bn(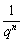 +qn)>2bn
+qn)>2bn
(2)设a、b、c为等差数列,则2b=a+c猜想 >(
>( )n(n≥2且n∈N*)
)n(n≥2且n∈N*)
下面用数学归纳法证明:
①当n=2时,由2(a2+c2)>(a+c)2,∴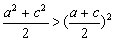
②设n=k时成立,即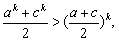
则当n=k+1时,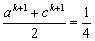 (ak+1+ck+1+ak+1+ck+1)
(ak+1+ck+1+ak+1+ck+1)
> (ak+1+ck+1+ak·c+ck·a)=
(ak+1+ck+1+ak·c+ck·a)= (ak+ck)(a+c)
(ak+ck)(a+c)
>( )k·(
)k·( )=(
)=( )k+1
)k+1
[例2]在数列{an}中,a1=1,当n≥2时,an,Sn,Sn-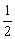 成等比数列.
成等比数列.
(1)求a2,a3,a4,并推出an的表达式;
(2)用数学归纳法证明所得的结论;
(3)求数列{an}所有项的和.
命题意图:本题考查了数列、数学归纳法、数列极限等基础知识.
知识依托:等比数列的性质及数学归纳法的一般步骤.采用的方法是归纳、猜想、证明.
错解分析:(2)中,Sk=- 应舍去,这一点往往容易被忽视.
应舍去,这一点往往容易被忽视.
技巧与方法:求通项可证明{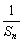 }是以{
}是以{ }为首项,
}为首项,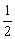 为公差的等差数列,进而求得通项公式.
为公差的等差数列,进而求得通项公式.
解:∵an,Sn,Sn-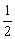 成等比数列,∴Sn2=an·(Sn-
成等比数列,∴Sn2=an·(Sn-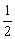 )(n≥2) (*)
)(n≥2) (*)
(1)由a1=1,S2=a1+a2=1+a2,代入(*)式得:a2=-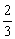
由a1=1,a2=-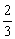 ,S3=
,S3= +a3代入(*)式得:a3=-
+a3代入(*)式得:a3=-
同理可得:a4=-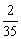 ,由此可推出:an=
,由此可推出:an=
(2)①当n=1,2,3,4时,由(*)知猜想成立.
②假设n=k(k≥2)时,ak=- 成立
成立
故Sk2=- ·(Sk-
·(Sk-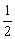 )
)
∴(2k-3)(2k-1)Sk2+2Sk-1=0
∴Sk=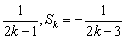 (舍)
(舍)
由Sk+12=ak+1·(Sk+1-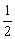 ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk-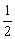 )
)
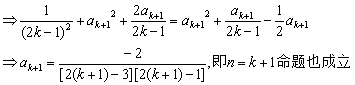
由①②知,an=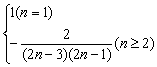 对一切n∈N成立.
对一切n∈N成立.
(3)由(2)得数列前n项和Sn=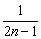 ,∴S=
,∴S=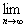 Sn=0.
Sn=0.
●锦囊妙记
(1)数学归纳法的基本形式
设P(n)是关于自然数n的命题,若
1°P(n0)成立(奠基)
2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.
(2)数学归纳法的应用
具体常用数学归纳法证明:恒等式,不等式,数的整除性,几何中计算问题,数列的通项与和等.
●歼灭难点训练
一、选择题
1已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n),则最大的m的值为( )
A.30 B.26 C.36 D.6
2.用数学归纳法证明3k≥n3(n≥3,n∈N)第一步应验证( )
A.n=1 B.n=2 C.n=3 D.n=4
二、填空题
3.)观察下列式子: …则可归纳出_________.
…则可归纳出_________.
4.)已知a1=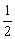 ,an+1=
,an+1=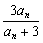 ,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.
,则a2,a3,a4,a5的值分别为_________,由此猜想an=_________.
三、解答题
5)用数学归纳法证明4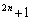 +3n+2能被13整除,其中n∈N*.
+3n+2能被13整除,其中n∈N*.
6.若n为大于1的自然数,求证: .
.
7.)已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+ )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
8.()设实数q满足|q|<1,数列{an}满足:a1=2,a2≠0,an·an+1=-qn,求an表达式,又如果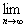 S2n<3,求q的取值范围.
S2n<3,求q的取值范围.
参考答案
难点磁场
解:假设存在a、b、c使题设的等式成立,这时令n=1,2,3,有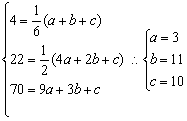
于是,对n=1,2,3下面等式成立
1·22+2·32+…+n(n+1)2=
记Sn=1·22+2·32+…+n(n+1)2
设n=k时上式成立,即Sk= (3k2+11k+10)
(3k2+11k+10)
那么Sk+1=Sk+(k+1)(k+2)2= (k+2)(3k+5)+(k+1)(k+2)2
(k+2)(3k+5)+(k+1)(k+2)2
= (3k2+5k+12k+24)
(3k2+5k+12k+24)
= [3(k+1)2+11(k+1)+10]
[3(k+1)2+11(k+1)+10]
也就是说,等式对n=k+1也成立.
综上所述,当a=3,b=11,c=10时,题设对一切自然数n均成立.
歼灭难点训练
一、1.解析:∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
证明:n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1-(2k+7)·3k
=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2(k≥2)
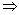 f(k+1)能被36整除
f(k+1)能被36整除
∵f(1)不能被大于36的数整除,∴所求最大的m值等于36.
答案:C
2.解析:由题意知n≥3,∴应验证n=3.
答案:C
二、3.解析: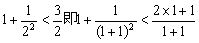

 (n∈N*)
(n∈N*)
 (n∈N*)
(n∈N*)
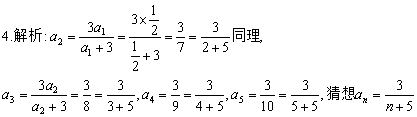
 、
、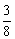 、
、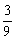 、
、
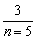
三、5.证明:(1)当n=1时,42×1+1+31+2=91能被13整除
(2)假设当n=k时,42k+1+3k+2能被13整除,则当n=k+1时,
42(k+1)+1+3k+3=42k+1·42+3k+2·3-42k+1·3+42k+1·3
=42k+1·13+3·(42k+1+3k+2)
∵42k+1·13能被13整除,42k+1+3k+2能被13整除
∴当n=k+1时也成立.
由①②知,当n∈N*时,42n+1+3n+2能被13整除.
6.证明:(1)当n=2时,
(2)假设当n=k时成立,即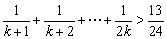

7.(1)解:设数列{bn}的公差为d,由题意得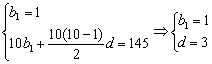 ,∴bn=3n-2
,∴bn=3n-2
(2)证明:由bn=3n-2知
Sn=loga(1+1)+loga(1+ )+…+loga(1+
)+…+loga(1+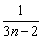 )
)
=loga[(1+1)(1+ )…(1+
)…(1+ 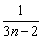 )]
)]
而 logabn+1=loga
logabn+1=loga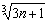 ,于是,比较Sn与
,于是,比较Sn与 logabn+1的大小
logabn+1的大小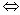 比较(1+1)(1+
比较(1+1)(1+ )…(1+
)…(1+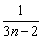 )与
)与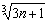 的大小.
的大小.
取n=1,有(1+1)=
取n=2,有(1+1)(1+
推测:(1+1)(1+ )…(1+
)…(1+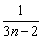 )>
)>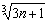 (*)
(*)
①当n=1时,已验证(*)式成立.
②假设n=k(k≥1)时(*)式成立,即(1+1)(1+ )…(1+
)…(1+ )>
)>
则当n=k+1时,

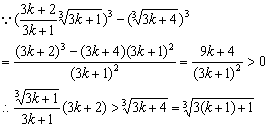
 ,即当n=k+1时,(*)式成立
,即当n=k+1时,(*)式成立
由①②知,(*)式对任意正整数n都成立.
于是,当a>1时,Sn> logabn+1,当 0<a<1时,Sn<
logabn+1,当 0<a<1时,Sn< logabn+1
logabn+1
8.解:∵a1·a2=-q,a1=2,a2≠0,
∴q≠0,a2=-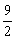 ,
,
∵an·an+1=-qn,an+1·an+2=-qn+1
两式相除,得 ,即an+2=q·an
,即an+2=q·an
于是,a1=2,a3=2·q,a5=2·qn…猜想:a2n+1=-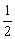 qn(n=1,2,3,…)
qn(n=1,2,3,…)
综合①②,猜想通项公式为an=
下证:(1)当n=1,2时猜想成立
(2)设n=2k-1时,a2k-1=2·qk-1则n=2k+1时,由于a2k+1=q·a2k-1
∴a2k+1=2·qk即n=2k-1成立.
可推知n=2k+1也成立.
设n=2k时,a2k=-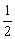 qk,则n=2k+2时,由于a2k+2=q·a2k,
qk,则n=2k+2时,由于a2k+2=q·a2k,
所以a2k+2=-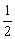 qk+1,这说明n=2k成立,可推知n=2k+2也成立.
qk+1,这说明n=2k成立,可推知n=2k+2也成立.
综上所述,对一切自然数n,猜想都成立.
这样所求通项公式为an=
S2n=(a1+a3…+a2n-1)+(a2+a4+…+a2n)
=2(1+q+q2+…+qn-1)-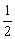 (q+q2+…+qn)
(q+q2+…+qn)

由于|q|<1,∴ =
=
依题意知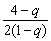 <3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
<3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
第二篇:数学归纳法
归纳法 (—)第一数学归纳法:
一般地,证明一个与正整数n有关的命题,有如下步骤: (1)证明当n取第一个值时命题成立;
(2)假设当n=k(k≥n的第一个值,k为自然数)时命题成立,证明当n=k+1时命题也成立。
(二)第二数学归纳法:
第二数学归纳法原理是设有一个与自然数n有关的命题,如果:
(1)当n=1回时,命题成立;
(2)假设当n≤k时命题成立,则当n=k+1时,命题也成立。 那么,命题对于一切自然数n来说都成立。
(三)螺旋归纳法:
螺旋归纳法是归纳法的一种变式,其结构如下:
Pi和Qi是两组命题,如果:
P1成立
Pi成立=>Qi成立
那么Pi,Qi对所有自然数i成立
利用第一数学归纳法容易证明螺旋归纳法是正确的
排列组合 ·阶乘:
n!=1×2×3×……×n,(n为不小于0的整数)
规定0!=1。
·排列
从n个不同元素中取m个元素的所有排列个数,
A(n,m)= n!/(n - m)! (m是上标,n是下标,都是不小于0的整数,且m≤n)
··组合
从n个不同的元素里,每次取出m个元素,不管以怎样的顺序并成一组,均称为组合。所有不同组合的种数
C(n,m)= A(n,m)/m!=n!/[m!·(n-m)!] (m是上标,n是下标,都是不小于0的整数,且m≤n)
◆组合数的性质:
C(n,k) = C(n,k-1) + C(n-1,k-1);
对组合数C(n,k),将n,k分别化为二进制,若某二进制位对应的n为0,而k为1 ,则C(n,k)为偶数;否则为奇数
◆整次数二项式定理(binomial theorem)
(a+b)^n=C(n,0)×a^n×b^0+C(n,1)×a^(n-1)×b+C(n,2)×a^(n-2)×b^2+...+C(n,n)×a^0×b^n
所以,有 C(n,0)+C(n,1)+C(n,2)+...+C(n,n)
=C(n,0)×1^n+C(n,1)×1^(n-1)×1+C(n,2)×1^(n-2)×1^2+...+C(n,n)×1^n =(1+1)^n = 2^n
微积分学
极限的定义:
设函数f(x)在点x。的某一去心邻域内有定义,如果存在常数A,对于任意给定的正数ε(无论它多么小),总存在正数δ ,使得当x满足不等式0<|x-x。|<δ 时,对应的函数值f(x)都满足不等式:
|f(x)-A|<ε
那么常数A就叫做函数f(x)当x→x。时的极限
几个常用数列的极限:
an=c 常数列 极限为c
an=1/n 极限为0
an=x^n 绝对值x小于1 极限为0
导数:
定义:f'(x)=y'=lim⊿x→0[f(x+⊿x)-f(x)]/⊿x=dy/dx 几种常见函数的导数公式:
① C'=0(C为常数函数);
② (x^n)'= nx^(n-1) (n∈Q);
③ (sinx)' = cosx;
④ (cosx)' = - sinx;
⑤ (e^x)' = e^x;
⑥ (a^x)' = (a^x) * Ina (ln为自然对数)
⑦ (Inx)' = 1/x(ln为自然对数 X>0)
⑧ (log a x)'=1/(xlna) ,(a>0且a不等于1)
⑨(sinh(x))'=cosh(x)
⑩(cosh(x))'=sinh(x)
(tanh(x))'=sech^2(x)
(coth(x))'=-csch^2(x)
(sech(x))'=-sech(x)tanh(x)
(csch(x))'=-csch(x)coth(x)
(arcsinh(x))'=1/sqrt(x^2+1)
(arccosh(x))'=1/sqrt(x^2-1) (x>1)
(arctanh(x))'=1/(1+x^2) (|x|<1)
(arccoth(x))'=1/(1-x^2) (|x|>1)
(chx)‘=shx, (ch为双曲余弦函数)
(shx)'=chx: (sh为双曲正弦函数)
(3)导数的四则运算法则:
①(u±v)'=u'±v'
②(uv)'=u'v+uv'
③(u/v)'=(u'v-uv')/ v^2
(4)复合函数的导数
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数(链式法则):
d f[u(x)]/dx=(d f/du)*(du/dx)。
[∫(上限h(x),下限g(x)) f(x)dx]’=f[h(x)]·h'(x)- f[g(x)]·g'(x)
洛必达法则(L'Hospital):
是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
设
(1)当x→a时,函数f(x)及F(x)都趋于零;
(2)在点a的去心邻域内,f'(x)及F'(x)都存在且F'(x)≠0;
(3)当x→a时lim f'(x)/F'(x)存在(或为无穷大),那么
x→a时 lim f(x)/F(x)=lim f'(x)/F'(x)。
再设
(1)当x→∞时,函数f(x)及F(x)都趋于零;
(2)当|x|>N时f'(x)及F'(x)都存在,且F'(x)≠0;
(3)当x→∞时lim f'(x)/F'(x)存在(或为无穷大),那么
x→∞时 lim f(x)/F(x)=lim f'(x)/F'(x)。
利用洛必达法则求未定式的极限是微分学中的重点之一,在解题中应注意:
①在着手求极限以前,首先要检查是否满足0/0或∞/∞型,否则滥用洛必达法则会出错。当不存在时(不包括∞情形),就不能用洛必达法则,这时称洛必达法则失效,应从另外途径求极限。比如利用泰勒公式求解。 ②洛必达法则可连续多次使用,直到求出极限为止。
③洛必达法则是求未定式极限的有效工具,但是如果仅用洛必达法则,往往计算会十分繁琐,因此一定要与其他方法相结合,比如及时将非零极限的乘积因子分离出来以简化计算、乘积因子用等价量替换等。 曲率
K = lim(Δs→0) |Δα/Δs|
当曲线y=f(x)存在二阶导数时,K=|y''|/(1+ y' ^2)^(3/2); 曲率半径R=1/K;
不定积分
设F(x)是函数f(x)的一个原函数,我们把函数f(x)的所有原函数F(x)+C(C为任意常数)叫做函数f(x)的不定积分。
记作∫f(x)dx。
其中∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数,求已知函数的不定积分的过程叫做对这个函数进行积分。
由定义可知:
求函数f(x)的不定积分,就是要求出f(x)的所有的原函数,由原函数的性质可知,只要求出函数f(x)的一个原函数,再加上任意的常数C,就得到函数f(x)的不定积分。
也可以表述成,积分是微分的逆运算,即知道了导函数,求原函数. ·基本公式:
1)∫0dx=c;
∫a dx=ax+c;
2)∫x^udx=(x^u+1)/(u+1)+c;
3)∫1/xdx=ln|x|+c
4))∫a^xdx=(a^x)/lna+c
5)∫e^xdx=e^x+c
6)∫sinxdx=-cosx+c
7)∫cosxdx=sinx+c
8)∫1/(cosx)^2dx=tanx+c
9)∫1/(sinx)^2dx=-cotx+c
10)∫1/√(1-x^2) dx=arcsinx+c
11)∫1/(1+x^2)dx=arctanx+c
12)∫1/(a^2-x^2)dx=(1/2a)ln|(a+x)/(a-x)|+c;
13)∫secxdx=ln|secx+tanx|+c
14)∫1/(a^2+x^2)dx=1/a*arctan(x/a)+c
15)∫1/√(a^2-x^2) dx=arcsin(x/a)+c;
16) ∫sec^2 x dx=tanx+c;
17) ∫shx dx=chx+c;
18) ∫chx dx=shx+c;
19) ∫thx dx=ln(chx)+c;
·分部积分法:
∫u(x)·v'(x) dx=∫u(x) d v(x)=u(x)·v(x) -∫v(x) d
u(x)=u(x)·v(x) -∫u'(x)·v(x) dx.
☆一元函数泰勒公式(Taylor's formula)
泰勒中值定理:若f(x)在开区间(a,b)有直到n+1阶的导数,则当函数在此区间内时,可以展开为一个关于(x-x0)多项式和一个余项的和:
f(x)=f(x0)+f'(x0)(x-x0)+f''(x0)/2!?(x-x0)^2,+f'''(x0)/3!?(x-x0)^3+……+f的n阶导数?(x0)/n!?(x-x0)^n+Rn
其中Rn=f(n+1)(ξ)/(n+1)!?(x-x0)^(n+1)为拉格朗日型的余项,这里ξ在x和x0之间。
定积分
形式为∫f(x) dx (上限a写在∫上面,下限b写在∫下面)。之所以称其为定积分,是因为它积分后得出的值是确定的,是一个数,而不是一个函数。
牛顿-莱布尼兹公式:若F'(x)=f(x),那么∫f(x) dx (上限a下限b)=F(a)-F(b)
牛顿-莱布尼兹公式用文字表述,就是说一个定积分式的值,就是上限在原函数的值与下限在原函数的值的差。
微分方程
凡是表示未知函数的导数以及自变量之间的关系的方程,就叫做微分方程。
微分方程差不多是和微积分同时先后产生的,苏格兰数学家耐普尔创立对数的时候,就讨论过微分方程的近似解。牛顿在建立微积分的同时,对简单的微分方程用级数来求解。后来瑞士数学家雅各布?贝努利、欧拉、法国数学家克雷洛、达朗贝尔、拉格朗日等人又不断地研究和丰富了微分方程的理论。
如果在一个微分方程中出现的未知函数只含一个自变量,这个方程就叫做常微分方程
特征根法是解常系数齐次线性微分方程的一种通用方法。
如 二阶常系数齐次线性微分方程y''+py'+qy=0的通解:
设特征方程r*r+p*r+q=0两根为r1,r2。
1 若实根r1不等于r2
y=C1*e^(r1x)+C2*e^(r2x).
2 若实根r=r1=r2
y=(C1+C2x)*e^(rx)
3 若有一对共轭复根 r1, 2=λ±ib :
y=e^(λx)·[C1·cos(bx)+ C2·sin(bx)]
