陈纪修教授《数学分析》九讲学习笔记与心得
云南分中心 × 昆明学院 × 周兴伟
此次听陈教授的课，收益颇多。陈教授的这些讲座，不仅是在教我们如何处理《数学分析》中一些教学重点和教学难点，更是几堂非常出色的示范课。我们不妨来温习一下。
第一讲、微积分思想产生与发展的历史
法国著名的数学家H.庞加莱说过：“如果我们想要预见数学的将来，适当的途径是研究这门科学的历史和现状。” 那么，如果你要学好并用好《数学分析》，那么，掌故微积分思想产生与发展的历史是非常必要的。陈教授就是以这一专题开讲的。
在学校中，我不仅讲授《数学分析》，也讲授《数学史》，所以我非常赞同陈教授在教学中渗透数学史的想法，这应该也是提高学生数学素养的有效途径。
在这一讲中，陈教授脉络清晰，分析精当，这是我自叹不如的。讲《数学史》也有些年头，但仅满足于史料的堆砌，没有对一些精彩例子加以剖析。如陈教授对祖暅是如何用 “祖暅原理”求出球的体积的分析，这不仅对提高学生的学习兴趣是有益的（以疑激趣、以奇激趣），而且有利于提高学生的民族自豪感（陈教授也提到了这一点）。
在这一讲中，陈教授对weierstrass的“ε?N”、“ε?δ”语言的评述是“它实现了静态语言对动态极限过程的刻画”。这句话是非常精当的，如果意识不到这一点，你就很难理解这一点。在此我还想明确一点：《数学分析》的研究对象是函数，主要是研究其分析性质，即连续性、可微性及可积性，而使用的工具就是极限。如果仔细盘点一下，在《数学分析》中，无论是数、函数、数列、函数列，数项级数，函数项级数等相关问题，无不用到这一语言，你应该能理解陈教授的“对于数学类学生来说，没有“ε?N”、“ε?δ”语言，在《数学分析》中几乎是寸步难行的”这一观点。
第二讲、实数系的基本定理
在这一讲中，陈教授从《实变函数》中对集合基数的讨论展开，对实数系的连续性作了有趣的讨论。首先是从绅士开party的礼帽问题，带我们走进了“无穷的世界”。
我在开《数学赏析》时有一个专题就是“无穷的世界”，我给学生讲礼帽问题、也讲希尔伯特无穷旅馆问题，但遗憾的是，当我剖析“若无穷旅馆住满了人，再来两个时，可将住１号房间的移往３号房间，住２号房间的移往４号房间，从而空出两个房间”时，学生对我“能移”表示怀疑。这一点我往往只能遗憾的说“跳不出有限的圈子，用有限的眼光来看无限，只能是‘只在此山中，云深不知处’”。当然，我还是会进一步考虑如何来讲好这一讲。若陈教授或其他老师有好的建议，能指点一下，则不胜感激。
对于集合[0,1]与(0,1)的对等关系，包括Q与Ｒ的对等关系，或者说他们之间双射的构造。关键在于“求同存异”，找一个可数集来“填补”他们之间的差距，这相当于希尔伯特无穷旅馆问题中来了两个人和来了可数个人。
对于实数集中的有理数，“廖若晨星”是非常形象的描述。一声集合的哨响，我们发现，有理数在实数轴上几乎是没有位置的（mQ=0），用一系列的帽子来盖住这些点，而这些帽子的大小是ε，这是非常精彩的结果。
从可数集到不可数集，再加上无最大基数定理，让我们看到了“无穷的层次性”，由此我们不难理解“人外有人，天外有天，无穷之外有无穷”。我们不能不发出“哀吾生之须臾，羡长江之无穷”的感慨。
陈教授对单调确界原理的证明非常清晰明了，几何直观的描述形象直观。
第三讲 《数学分析》课程中最重要的两个常数
法国著名雕塑家罗丹曾经说过“生活中从不缺少美，而是缺少发现美的眼睛”。我想说：“数学中并不缺少美，缺少的是揭示数学美的老师”。陈教授是一个出色的老师，他不仅发现了数学的美，而且为我们展示了数学的美。
著名的欧拉公式：
，实现了有理数、无理数、超越数、实数、虚数完美统一，获得“最美的数学定理”称号。欧拉建立了在他那个时代，数学中最重要的几个常数（
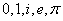）之间的绝妙的有趣的联系，被认为是数学奇异美的典例。
在本讲中，陈教授以李大潜院士访问法国“引入”的一个有趣例子开讲，让我们体会了数学中的美，这个不等式还有许多有意思的地方，无论是不等式的形式，还是他的证明，都非常深刻地体现了数学的美。Pi是无理数的证明，吸引了与会学员的眼球，赞叹之余，有学员问这一证法的出处，我也还真想知道，请陈教授不吝指教。
本讲最后将函数sinx/x展成无穷乘积形式，并妙用此形式求出p级数中p为偶数值时的和，对我而言是耳目一新的。在我记忆中好像菲尔金哥尔茨的《微积分学教程》(第二卷)中也有求出的方法，而p为奇数的情形好像至今尚未解决。对p=2的情形，欧拉至少用两种方法得到结果，其中一种方法妙用了L’Hospital法则(《数学译林》09.3)。
第四讲 级数与反常积分收敛的A.D判别法
恰逢这个学期讲《数学分析》(3)，在讲授含参变量反常积分时，先复习了反常积分，再复习了函数项级数，并将几个判别法列表比较，尤其是A.D判别法，能与陈教授不谋而合，真是倍感荣幸。
陈教授对Abel引理的直观刻画，也是深得学员好评。我对陈教授从Abel引理分析Sanbn收敛条件的分析而得到Dilichlet判别法和Abel判别法的相关条件深感佩服，尤其是分析得丝丝入扣。
第五讲 函数项级数与含参变量反常积分的一致收敛
一致收敛性无疑是《数学分析》中的一个重要概念。陈教授对“点点收敛”与“一致收敛”的剖析是非常到位的，学生在学习时如果是只能注意到在定义的陈述“"x”的位置不相同，而不明其所以时，这样的教学肯定是失败的。陈教授例子选择精当，语言使用精辟，问题分析精准。
请注意陈教授的这句话：“毛病出在点态收敛的情况下，在某些点附近，N无法控制”（类似的话在第九讲中说过）。
第六讲 Weierstrass函数：处处连续处处不可导的函数
陈教授分析了为何在Weierstrass之前的数学家不能构造出这样的函数。原来在此之前，数学家们所掌握的函数是不足以构造出这样的函数的。
Weierstrass在1872年构造出了如下处处连续处处不可导的函数：
Sansin(bnx) 0<a<1<b, ab>1
陈教授选用1930年Van Der Waerden给出的例子进行了剖析。所讲自是精当，本人很是受益。
第七讲 条件极值问题与Lagrange乘数法
本讲陈教授从一个几何问题入手，得到一个条件极值问题。考虑了条件极值的必要条件，引入Lagrange乘数法，化条件极值问题为无极条件极值问题。这部分内容中，本人认为几何解释最有启发性。
对于具体使用Lagrange乘数法的例子中，如何解方程组，陈教授给了很好的建议。第二个例子，即求平面x+y+z=0与椭球面x2+y2+4z2=1相交而成的椭圆面积。这个例子我很喜欢，只可惜不能用来做期末考题（不要问我为什么！）。
第八讲 重积分的变量代换
本讲陈教授从定积分的换元的计算公式分析入手，对二重积分的相应的代换公式作出类比猜想（在教学中注重渗透数学思想方法，如此妙哉！）再作分析，然后得出代换公式。
为证明代换公式，陈教授引入本原映射，化“矩形”为“梯形”，化变换T为两个本原变换的复合，实现了化复杂为简单，化困难为容易。
第九讲 《数学分析》课程中的否定命题
《数学分析》教学中，说说“反话”很重要！（请不要误解！）
两个命题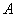
与
如果既不能同时成立，也不能同时不成立，就称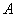与互为否定命题。
若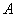与互为否定命题，则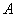与一定满足：一个成立，另一个必然不成立；一个不成立，另一个必定成立。（废话！）
有界与无界、收敛于a与不收敛于a、收敛与不收敛、（注意前边两对的区别！）、可导与不可导、Cauchy收敛准则及其否定命题，等等。这些“反话”不说，大量的题做不了。
我在讲《数学分析》(1)时会有一讲（几个概念的否定叙述）就是来讲否定命题的。
陈教授在这部分的例子非常好，分析得也清楚！
陈教授的九讲，给了我们太多的启示：
一、在我们的教学中，不仅要教其所以然，而且要教其所以然。陈教授的这九讲，应该是我们讲授《数学分析》的经典案例，当然，我们不一定是讲这一些内容！正确的思想从哪里来，是从天上掉下来的吗？不是！
二、在我们的教学，不仅要传授知识，而且要传授思想方法，也就是教学中要注
重思想方法的渗透。
三、在我们的教学中，不仅要传授知识，而且要培养学生的数学素养，让他们了解数学的过去、现在，以便开创数学的将来。
四、在我们的教学中，或许会遇的许多困难：教学时数少，教学对象差等等，但我们应从我们自身积极的寻找对策。陈教授就是这样的。
以上所述，仅凭个人听课记录，又仅凭个人理解。若是有误，请陈教授见谅并斧正。
最后，向陈纪修教授致以崇高的敬意！
滇源后学：周兴伟
第二篇：数学分析课后习题答案--高教第二版(陈纪修)--10章
第十章 函数项级数
习 题 10. 1 函数项级数的一致收敛性
1. 讨论下列函数序列在指定区间上的一致收敛性。
⑴ Sn(x) = e?nx , (i) x∈(0,1)， (ii) x∈(1,+∞)； ⑵ Sn(x) = xe?nx, x∈(0,+∞)；
x∈(?∞,+∞)， (ii) x∈[?A,A](A>0)； ⑶ Sn(x) = sin, (i)
x∈(0,1)， (ii) x∈(1,+∞)； ⑷ Sn(x) = arctan nx, (i)
1
, x∈(?∞,+∞)； 2n
⑹ Sn(x) = nx(1 - x)n , x∈[0,1]；
xx
⑺ Sn(x) =ln, (i) x∈(0,1)， (ii) x∈(1,+∞))；
nnxn
⑻ Sn(x) = , (i) x∈(0,1)， (ii) x∈(1,+∞)；
1+xn
⑼ Sn(x) = (sin x)n , x∈[0,π]；
xn
⑸ Sn(x) =
x2+
⑽ Sn(x) = (sin x), (i) x∈[0,π]， (ii) x∈[δ,π?δ]（δ>0）；
x? ⑾ Sn(x) = ?x∈(0,A](A>0)； ?1+?, (i) x∈(0,+∞)， (ii)
n??
??1
?⑿ Sn(x) = n?x+?x?x∈(0,+∞), (ii)x∈[δ,+∞),δ>0。 ?, (i) n??
课
， d(Sn,S)=supSn(x)?S(x)=1 ─/→ 0（n→∞）
x∈(0,1)
所以{Sn(x)}在(0,1)上非一致收敛。 (ii) S(x)=0，
d(Sn,S)=supSn(x)?S(x)=e?n→0(n→∞)，
x∈(1,+∞)
所以{Sn(x)}在(1,+∞)上一致收敛。 （2）S(x)=0，
d(Sn,S)=supSn(x)?S(x)=
x∈(0,+∞)
后
解 （1）(i) S(x)=0，
答案
网 w
n
ww
1
1n
.k
1
→0(n→∞)， ne
hd
aw
.c
om
所以{Sn(x)}在(0,+∞)上一致收敛。 （3）(i) S(x)=0，
d(Sn,S)=
sup
x∈(?∞,+∞)
， Sn(x)?S(x)=1 ─/→ 0（n→∞）
所以{Sn(x)}在(?∞,+∞)上非一致收敛。 (ii) S(x)=0，当n>
2A
π
，
A
→0(n→∞)， n
d(Sn,S)=supSn(x)?S(x)≤
x∈[?A,A]
2
x∈(0,1)
所以{Sn(x)}在(0,1)上非一致收敛。
2
网 w
(ii)S(x)=
π
，
所以{Sn(x)}在(1,+∞)上一致收敛。
后
答案
d(Sn,S)=supSn(x)?S(x)=
x∈(1,+∞)
ww
π
2
?arctann→0(n→∞)，
课
（5）S(x)=x，由于Sn(x)?S(x)=x2+
d(Sn,S)=
sup
x∈(?∞,+∞)
Sn(x)?S(x)→0(n→∞)，
所以{Sn(x)}在(?∞,+∞)上一致收敛。 （6）S(x)=0，
111
， Sn(?S()=(1?)n ─/→ 0（n→∞）
nnn
所以{Sn(x)}在[0,1]上非一致收敛。
（7）(i) S(x)=0，由于Sn(0+)?S(0+)=0，且
2
.k
11
?≤，于是 x2
nn
hd
d(Sn,S)=supSn(x)?S(x)=
π
2
─/→ 0（n→∞），
aw
.c
（4）(i) S(x)=
π
，
om
所以{Sn(x)}在[?A,A]上一致收敛。
d[Sn(x)?S(x)]=1(1+lnx)<0 (n≥2)， dxnn
于是
d(Sn,S)=supSn(x)?S(x)=
x∈(0,1)lnn→0(n→∞)， n
所以{Sn(x)}在(0,1)上一致收敛。 (ii) S(x)=0，
Sn(2n)?S(2n)=2ln2 ─/→ 0（n→∞）， (ii) S(x)=1，
π?1=x?1π?2S(x)=?，取xn∈[0,π]，使得sinxn=1?，则xn≠， （9）πn2?0x∈[0,π],x≠?2?
1Sn(xn)?S(xn)=(1?n ─/→ 0（n→∞）， n
所以{Sn(x)}在[0,π]上非一致收敛。
（10）(i)S(x)=??0x=0,π1 ，取xn∈(0,π)，使得sinxn=n，则 2?10<x<π
课所以{Sn(x)}在(1,+∞)上非一致收敛。 后1(1+)n11?1 ─/→ 0（n→∞）， Sn(1+)?S(1+=1nnn1+(1+)n答案网 www3所以{Sn(x)}在(0,1)上非一致收敛。 .k1(1?)n11 ─/→ 0（n→∞）， Sn(1?)?S(1?)=1nnn1+(1?)nhdaw.c（8）(i) S(x)=0， om所以{Sn(x)}在(1,+∞)上非一致收敛。
Sn(xn)?S(xn)=
1
， ?1 ─/→ 0（n→∞）
2
所以{Sn(x)}在(0,π)上非一致收敛。 (ii) S(x)=1，
d(Sn,S)=
sup
x∈[δ,π?δ]
Sn(x)?S(x)
1
=1?sinn
δ→0(n→∞)，
所以{Sn(x)}在[δ,π?δ]上一致收敛。 （11）(i)S(x)=ex，
(ii)S(x)=ex，由于Sn(0+)?S(0+)=0，且当n充分大时，
d
[Sn(x)?S(x)]=??1+dx?
x?
?n?
n?1
网 w
于是
ww
n
A
所以{Sn(x)}在(0,A]上一致收敛。
课
（12）(i)S(x)=
后
2x
113??
， Sn(?S()=?2??n ─/→ 0（n→∞）
nn2??
所以{Sn(x)}在(0,+∞)上非一致收敛。 (ii)S(x)=
12x
，
1x+1
+xn
4
??1?Sn(x) = n?x+?x??=n??
答案
A??
d(Sn,S)=supSn(x)?S(x)=e??1+?→0(n→∞)，
n?x∈(0,A]?
1
，
.k
<
?ex<0，
hd
12x
aw
=S(x)，
.c
所以{Sn(x)}在(0,+∞)上非一致收敛。
om
Sn(n)?S(n)=2n?en ─/→ 0（n→∞），
由于
d
[Sn(x)?S(x)]=dx
?1
11
2x(x+(x+x+)
nn
+1
3
4x2
>0，
可知
d(Sn,S)=supSn(x)?S(x)=Sn(δ)?S(δ)
x∈[δ,+∞)
??11?=?n?+??+?2→0(n→∞)， n??
hd
lim
n→∞
∫S
1
n
(x)dx ≠
∫limSn(x) dx。
0n→∞
1
aw
2. 设Sn(x) = n( xn -x2n )，则函数序列{Sn(x)}在[0,1]上收敛但不一致
收敛，且极限运算与积分运算不能交换，即
.c
由于
1
答案
11
lim∫Sn(x)dx=lim∫0n(x?x)dx=，∫limSn(x) dx=0， 0n→∞n→∞0n→∞2
1
所以
后
3. 设Sn(x) =
⑴ 函数序列{Sn(x)}在(?∞,+∞)上一致收敛；
d? ⑵ ?Sn(x)?在(?∞,+∞)上不一致收敛； ?
?dx
?
⑶ 极限运算与求导运算不能交换，即
dd
Sn(x) = limSn(x) n→∞dxdxn→∞
并不对一切x∈(?∞,+∞)成立。
x
，S(x)=0，则 解 （1）Sn(x)=22
1+nx
x1
→0(n→∞)， ≤Sn(x)?S(x)=22
2n1+nx
lim
5
课
lim∫0Sn(x)dx ≠
n→∞
x
，则 22
1+nx
1
网 w
11??
Sn(xn)?S(xn)=n?(1?)n?(1?)2n?→+∞，
nn??
所以{Sn(x)}在[0,1]上非一致收敛。
n
2n
ww
∫limSn(x) dx。
0n→∞
1
.k
证 函数序列{Sn(x)}在[0,1]上收敛于S(x)=0。取xn=1?，则
om
1n
所以{Sn(x)}在[δ,+∞)上一致收敛。
所以{Sn(x)}在(?∞,+∞)上一致收敛。
?1x=0dd1?n2x2
，σ(x)=limSn(x)=?， （2） Sn(x)=222→∞n≠0x0dxdx(1+nx)?
1
取xn=，则
2n
d12
─/→ 0（n→∞）， Sn(xn)?σ(xn)=
dx25d?
所以?S(x)??在(?∞,+∞)上不一致收敛。 n
dx??
（3）由于在x=0处，
dd
Sn(x)=1， limSn(x)=0，σ(x)=lim
n→∞→∞ndxdx
所以在x=0处，
ddSn(x) =limlimSn(x) n→∞dxdxn→∞
不成立。
问极限运算与求导运算能否交换，即 是否成立?
4. 设Sn(x) =arctan xn ，则函数序列{Sn(x)}在(0,+∞)上一致收敛；试
lim
S(x)=limSn(x)=0，S'(x)=0，
n→∞
'
所以 limSn(1)=
n→∞
1
≠S'(1)，即 2ddSn(x) =limlimSn(x) n→∞dxdxn→∞
在x=1不成立。
5. 设Sn(x) =nαxe?nx，其中a是参数。求a的取值范围，使得函数序列
{Sn(x)}在[0,1]上 ⑴ 一致收敛；
⑵ 积分运算与极限运算可以交换，即
lim
n→∞
课
后
答案
xn?11n'
， 解 Sn(x)=arctanx，Sn(x)=2n
n1+x
网
w
∫S
1
n
(x)dx =
⑶ 求导运算与极限运算可以交换，即对一切x∈[0,1]成立
lim
n→∞
ddSn(x) = limSn(x) 。 dxdxn→∞
6
ww
1
n→∞
dd
Sn(x) =limSn(x) dxdxn→∞
∫limSn(x) dx；
0n→∞
.k
hd
1
n
aw
.c
om
'(x)=nαe?nx(1?nx)=0，得到x=，即 解 (1) S(x)=limSn(x)=0，令Snn→∞1n
1d(Sn,S)=supSn(x)?S(x)=Sn(=nα?1e?1， nx∈[0,1]
所以当α<1时，{Sn(x)}在[0,1] 所以limd(Sn,S)=0当且仅当α<1时成立，n→∞
上一致收敛。
(2) ∫0limSn(x)dx=∫0S(x)dx=0，∫0Sn(x)dx=nα?2?nα?1(1+)e?n， n→∞所以当且仅当α<2时，成立.
limn→∞1111n ∫S01n(x)dx = ∫limSn(x) dx。 0n→∞1
n→∞
limn→∞
对一切x∈[0,1]成立。
6. 设S '(x)在区间(a,b)上连续，
答案??1?x+?S(x) Sn(x) = n?S????， ??n??
上一致收敛于S'(x)。
取0<α<η, 则S'(x)在[a+α,b?α]上一致连续, 即 ?ε>0,?δ>0, ?x',x"∈[a+α,b?α], 只要x'?x"<δ, 就成立 课解 显然limSn(x)=S'(x)，所以只须证明 ?η>0, {Sn(x)}在[a+η,b?η]n→∞后证明：{Sn(x)}在(a,b)上内闭一致收敛于S '(x)。
S'(x')?S'(x")<ε。 ??1??1??取N=max??,???, 则当n>N且x∈[a+η,b?η]时，有 δηα???????
x+1∈[a+α,b?α], n
7 网 wddSn(x)=limSn(x) dxdxn→∞ww.k所以当且仅当α<0时， hdlime?nx?0x∈(0,1]， =(1?nx)??1x=0aw.c由于 om(3) dddSn(x)=nαe?nx(1?nx)， limSn(x)=S(x)=0，dxn→∞dxdx
于是
Sn(x)?S'(x)=S'(ξ)?S'(x)<ε，
所以{Sn(x)}在(a,b)上内闭一致收敛于S '(x)。 7. 设S0(x)在[0,a]上连续，令
Sn(x) =
证 设S0(x)≤M, 则
S1(x)=
∫
x
Sn?1(t)d t， n =1,2,"。
证明：{Sn(x)}在[0,a]上一致收敛于0。
∫0S0(t)dt≤Mx，
x
x
x
所以{Sn(x)}在[0,a]上一致收敛于0。
证 S(x)在[0,1]上连续，所以有界，设S(x)≤M。 由S(1)=0, 可知
?ε>0,?δ>0, ?x∈[1?δ,1]，成立xnS(x)<ε。
由于{xn}在[0,1?δ]上一致收敛于零，可知
?N, ?n>N, ?x∈[0,1?δ]，成立 xn<
课
8. 设S(x)在[0,1]上连续，且S(1) = 0。证明：{xn S(x)}在[0,1]上一致收敛。
后
答案
xnanan
，lim(M=0， ≤MM
n→∞n!n!n!
网 w
由于
ww
ε
M
"
.k
tn?1xn
Sn(x)=∫0Sn?1(t)dt≤∫0Mdt=M，
(n?1)!n!
x
x
hd
aw
，
xnS(x)<ε
8
"
于是
.c
x2
， S2(x)=∫0S1(t)dt≤∫0Mtdt=M2!
om
对一切x∈[0,1]成立，因此{xn S(x)}在[0,1]上一致收敛。
课后答案网
习 题 10.2 一致收敛级数的判别与性质
1. 讨论下列函数项级数在所指定区间上的一致收敛性。 ⑴ ⑵
⑶
∞
∑(1?x)x
n=0∞
n
， x∈[0, 1]；
∑(1?x)
2
n=0∞
2
xn， x∈[0, 1]；
∑x3e?nx， x∈[0,+∞)；
n=0
⑷ ∑xe
n=0
∞
∞
?nx2
， (i) x∈[0,+∞)， (ii) x∈[δ,+∞)（δ＞0）；
⑹ ⑺
∑
n=1∞n=0
课
x2
⑿ ∑(?1)， x∈(-∞, +∞)。 2n
(1+x)n=0
∞
n
解（1）Sn(x)=∑(1?x)xk=1?xn+1 ，
k=0
后
n
答案
(?1)n
⑻ ∑， x∈(-∞, +∞)； 2
n+xn=1∞
1
⑼ ∑2nsinn， (i) x∈(0, +∞)，(ii) x∈[δ,+∞)（δ＞0）；
3xn=0
∞
sinxsinnx
⑽ ∑， x∈(-∞, +∞)；
nn=1
∞
x2
⑾ ∑， x∈(-∞, +∞)； 2n
n=0(1+x)
网 w
由于{x
n+1
}在[0,1]非一致收敛，所以∑(1?x)x
n=0
ww
∞
.k
∞
（2）设un(x)=(1?x)2xn，则在[0,1]上
0≤un(x)≤un(
∞
4n
， )<2
n+2(n+2)
∞
42n
由于∑收敛，由Weierstrass判别法，(1?x)x在[0,1]上一致∑2
n=0(n+2)n=0
1
hd
n
∑(?1)
n
(1?x)xn， x∈[0, 1]；
aw
在[0,1]上非一致收敛。
n+x
44
， x∈(-∞, +∞)；
.c
om
⑸
x
， x∈(-∞, +∞)； ∑32
n=01+nx∞
sinnx
收敛。
（3）设un(x)=x3e?nx，则当n≥1时，在[0,+∞)上
0≤un(x)≤un(
3
2
3K)=3， 2n
n2
∞∞K23?2
e。由于∑3收敛，由Weierstrass判别法，∑x3e?nx在其中K=4n=0n=0
n2
[0,+∞)上一致收敛。
aw
k=n+1
∑uk(xn)=
?2?nx2
m
xne
2
?(n+1)xn
+xne
2
?(n+2)xn
+"+xne
2?2nxn
.c
∈[0,+∞)，则
>nxne
om
（4）(i) 设un(x)=xe
?nx2
，对任意的正整数N，取m=2n(n>N)与xn=
2
?2nxn
1n
=ne
→+∞(n→∞)，
.k
所以∑xe
n=0
∞
hd
∞
2
不满足Cauchy收敛原理的条件，由此可知∑xe?nx在
[0,+∞)上非一致收敛；
(ii) 设un(x)=xe所以
?nx2
，则当n>
答案
网 w
1
2δ
2
由于∑δe
n=0
∞
课
后
0≤un(x)≤δe
ww
n=0
时，un(x)关于x在[δ,+∞)上单调减少，
?δ2n
，
∞
?nx2
?δ2n
收敛，由Weierstrass判别法，∑xe
n=0
在[δ,+∞)上一致收
敛。
∞x11n≥1（5）设un(x)=，则当时，u(x)≤，由于∑3收敛，n323
1+nxn=0
22n2n2
由Weierstrass判别法，∑（6）设un(x)=
sinnx
x
在(?∞,+∞)上一致收敛。 32
n=01+nx
∞
n+x
44
，则当n≥1时，un(x)≤
1
4n3
，由于∑
∞
1
4n=0
n3
收敛，
2
由Weierstrass判别法，∑n=1
∞
sinnxn+x
4
4
在(?∞,+∞)上一致收敛。
（7）设an(x)=(1?x)xn，bn(x)=(?1)n，则{an(x)}对固定的x∈[0,1]关于n是单调的，且在[0,1]上一致收敛于零，同时∑bk(x)≤1，由Dirichlet
k=0n
判别法，∑(?1)n(1?x)xn在[0,1]上一致收敛。
n=0
∞
（8）设an(x)=
1n
b(x)=(?1)，，则{an(x)}对固定的x∈(?∞,+∞)关于n2
n+x
3x
n
un(xn)=2n→+∞，
网 w
ww
（9）(i) 设un(x)=2nsin
1
，取xn=
.k
23π
n
∞n=0
hd
∈(0,+∞)，则
(?1)n
在(?∞,+∞)上一致收敛。 判别法，∑2
n=1n+x
∞
答案
即{un(x)}在(0,+∞)上非一致收敛，所以∑2nsin
课
后
敛；
(ii) 设un(x)=2nsin
13x
n
，则当x∈[δ,+∞)时，
1?2?
un(x)≤??，
δ?3?
n
∞
1?2?1
由Weierstrass判别法，∑2nsinn在[δ,+∞)上一致由于∑?收敛，
3xn=0δ?3?n=0
∞
n
收敛。 （10）设an(x)=
1n
，bn(x)=sinxsinnx，由于an(x)与x无关且单调趋于
3
aw
13nx
.c
k=1
n是单调的，且在(?∞,+∞)上一致收敛于零，同时
∑bk(x)
n
在(0,+∞)上非一致收
om
≤1，由Dirichlet
零，所以{an(x)}对固定的x∈(?∞,+∞)关于n是单调的，且在(?∞,+∞)上一致收敛于零，同时
xnxx1x
∑bk(x)=cos∑2sinsinkx=cos?cos(n+x?cos≤2，
2k=12222k=1
n
由Dirichlet判别法，∑
n=1
∞
sinxsinnx
n
在(?∞,+∞)上一致收敛。
网 w
x2n
b(x)=(?1)，，则{an(x)}对固定的x∈(?∞,+∞)关（12）设an(x)=n2n
(1+x)
ww
.k
(?∞,+∞)上非一致收敛。
hd
∞
x2x2
所以∑不满足Cauchy收敛原理的条件，由此可知∑在2n2n
n=0(1+x)n=0(1+x)
aw
∞
.c
1x2
ε=>0，对任意的正整数N，取，取（11）设un(x)=022n
e(1+x)
1
m=2n(n>N)与xn=∈(?∞,+∞)，则
n2222mxnxnxnnxn1
>++"+>=ε0， ∑uk(xn)=2n+12n+222n22n2
(1+xn)(1+xn)(1+xn)(1+xn)ek=n+1
于n是单调的，且在(?∞,+∞)上一致收敛于零，同时∑bk(x)≤1，由
x2
在(?∞,+∞)上一致收敛。 Dirichlet判别法，∑(?1)2n
(1+x)n=0
∞
n
后
cosnx
在(0,2π)上连续，且有连续的导函数。 2
n=0n+1
∞∞cosnxcosnx11
证 由于2，由Weierstraass判别法，≤2∑2收敛，∑2
n+1n+1n=0n+1n=0n+1
∞
cosnx
在(0,2π)上一致收敛，所以f(x)=∑2在(0,2π)上连续。
n=0n+1
∞cosnx∞nsinnxn?
设σ(x)=∑(2)'=?∑2，由于?单调趋于零，且对任 ?2
?n+1?n=0n+1n=0n+1
意的0<δ<π，当x∈[δ,2π?δ]时，
课
2. 证明：函数f(x)=∑
1?x?
coscos+nx???n
2?21?
sinkx=≤， ∑δxk=1
sin2sin
22
4
答
案
∞
om
nk=1
nsinnx
在[δ,2π?δ]上一致收敛，即2
n=0n+1
∞nsinnx∞nsinnx
在(0,2π)上内闭一致收敛，因此σ(x)=?∑2在(0,2π)?∑2
n+1n+1n=0n=0
上连续。再由逐项求导定理，可知f'(x)=σ(x)在(0,2π)上成立，即
∞
cosnx
在(0,2π)上有连续的导函数。 f(x)=∑2
n=0n+1
由Dirichlet 判别法，可知?∑
∞
3. 证明：函数f(x)=∑ne?nx在(0,+∞)上连续，且有各阶连续导函数。
n=1
∞
证 对任意的0<a<A<+∞，当x∈[a,A]，成立0<ne收敛，由Weierstraass判别法，∑ne
n=0∞
?nx
?nx
≤ne
?an
，且∑ne?an
n=0
∞
在[a,A]上一致收敛，即∑ne?nx在
n=0
∞
n=0
n=0n=0
aw
设σ(x)=
∑(ne
∞
?nx
)'=?∑ne
∞
.c
(0,+∞)上内闭一致收敛，所以f(x)=∑ne?nx在(0,+∞)上连续。
2?nx
∞
om
∞n=0
，与上面类似可证明?∑n2e?nx在
n=0
∞
∞
上有连续的导函数。
k∞n=1
注意到(?1)∑nk+1e?nx(k=1,2,")在(0,+∞)上都是内闭一致收敛的，
答
案
网 w
ww
项求导定理，可知f'(x)=σ(x)在(0,+∞)上成立，即f(x)=∑ne?nx在(0,+∞)
.k
n=0
(0,+∞)上内闭一致收敛，因此σ(x)=?∑n2e?nx在(0,+∞)上连续。再由逐
hd
所以上述过程可以逐次进行下去，由数学归纳法，可知f(x)=∑ne?nx
n=1
∞
(?1)n
在(0,+∞)上连续，且有各阶连续导函数。 ∑x
n=1n
∞
111
证 设f(x)=∑x，对任意1<a<A<+∞，当x∈[a,A]，成立0<x≤a，
nnnn=1
∞∞
11
且∑a收敛，由Weierstraass判别法，∑x在[a,A]上一致收敛，即 n=1nn=1n∞∞
11在上内闭一致收敛，所以在(1,+∞)上连续。 (1,+∞)f(x)=∑∑xx
n=1nn=1n
∞lnnd?1?lnn
又??=?，且对任意1<a<A<+∞，?∑x在[a,A]上一致收dx?n?nn=1n
∞
课
4. 证明：函数∑
后
∞
在(0,+∞)上有各阶连续导函数。
1
在(1,+∞) 上连续，且有各阶连续导函数；函数 x
n=1n
5
∞lnnlnn
敛，即?∑x在(1,+∞)上内闭一致收敛，则?∑x在(1,+∞)上连续。
n=1nn=1n
∞lnn
由逐项求导定理，可知f'(x)=?∑x，即f(x)在(1,+∞)上有连续导
n=1n
∞
函数。
k∞lnkndk?1?klnnk
可以证明(?1)∑x在(1,+∞)利用k?x?=(?1)(k=1,2,")，x
dx?n?nn=1n
上内闭一致收敛，同理可得f(x)在(1,+∞)上有各阶连续导函数。
(?1)n
设g(x)=∑x，由Dirichlet判别法，可知对任意0<a<A<+∞，
n=1n
∞
∞(?1)n(?1)n
即∑x在(0,+∞)上内闭一致收敛，所以∑x在[a,A]上一致收敛，
n=1nn=1n
∞
(?1)n+1lnn
在(0,+∞)上连续。由逐项求导定理，上内闭一致收敛，所以∑x
nn=1
∞
dk
利用k
dx
∞
课
(?1)n+1lnn
，即g(x)在(0,+∞)上有连续导函数。 可知g'(x)=∑x
nn=1
∞
后
?(?1)n??nx?
(?1)n+klnkn
可以证明∑在(0,+∞)上内闭一致收敛，同理可得g(x)在x
nn=1
(0,+∞)上有各阶连续导函数。
答案
?(?1)n+klnkn?=(k=1,2,")，同样由Dirichlet判别法，x?n?
5. 证明：函数项级数f(x)=∑arctan
x
可以逐项求导，即 2nn=1
∞ddx
f (x) = ∑(arctan2)。
dxnn=1dx
6
网 w
∞(?1)n+1lnn(?1)n+1lnn
0<a<A<+∞，∑在[a,A]上一致收敛，即∑在(0,+∞)xx
nnn=1n=1
∞
ww
d?(?1)n
又?x
dx??n?(?1)n+1lnn
?=，同样由Dirichlet判别法，可知对任意x?n?
.k
hd
(?1)n
g(x)=∑x在(0,+∞)上连续。
n=1n
∞
aw
.c
om
∞
证 函数项级数f(x)=∑arctan
n=1
∞
x
对一切x∈(?∞,+∞)收敛，且 2n
dx(arctan2)=dxn
1x22
n+2
n
，
∞d1x
≤，由Weierstraass判别法，可知由于(arctan ∑222xnnn=1dxn2+2
n
1
在(?∞,+∞)上一致收敛，再由逐项求导定理，即可知道
n=1
aw
n
6. 设数项级数
∞
∑a
∞
n
收敛，证明：
1∞
.k
∞
an
⑴ lim∑x = ∑an； ⑵
x→0+
n=1nn=1
∫0∑anxdx = ∑
n=1
hd
ww
证 (1) 首先对于每一固定的x∈[0,δ)(δ>0)，
n
∞
1
一切x∈[0,δ)与一切n，成立0<x≤1，又因为∑an是数项级数，它的
nn=1
答案
网 w
.c
an
。 n=1n+1
∞
1
x
关于n单调，且对于
om
∞
d
f (x) = dxdx
(arctan2)。
nn=1dx
∑
∞
收敛意味着关于x的一致收敛性，于是由Abel判别法，∑
an
x
后
n=1n
在[0,δ)上
课
一致收敛，因此和函数∑
∞
an
x
n=1n
关于x在[0,δ)连续，从而成立
∞
∞
an
lim∑x=∑an。 x→0+
n=1nn=1
(2) 由例题10.2.4，∑anxn在[0,1]上一致收敛，再由逐项积分定理，得
n=1
∞
到
∫0∑anxdx=∑
n
n=1
1∞
an
。 n=1n+1
∞
7. 设un (x)，vn (x)在区间(a, b)连续，且│un (x)│≤vn (x) 对一切n∈N+
7
成立。证明：若∑vn(x)在(a, b)上点态收敛于一个连续函数，则
n=1
∞
∑u
n=1
∞
n
(x)也必然收敛于一个连续函数。
证 设任意闭区间[c,d]?(a,b)。由于vn(x)≥0在[c,d]连续，和函数
∑v
n=1
∞
n
(x)在[c,d]连续，则由Dini定理可知∑vn(x)在[c,d]一致收敛。于
n=1
∞
是由Cauchy收敛原理，可知?ε>0，?N，?m>n>N，?x∈[c,d]，成 立
n=1n=1
n=1
ww
8. 设函数项级数
网 w
∑un(x)在x = a与x = b收敛，且对一切n∈N，
n=1
∞n=1
∞
.k
[c,d]?(a,b)的任意性，即得到∑un(x)在(a,b)连续。
+
∞
un (x)在闭区间[a,b]上单调增加，证明：∑un(x)在[a, b]上一致收敛。 证 由于∑un(x)在x = a与x = b收敛，由Cauchy收敛原理，可知
n=1∞
后
答案
课
?ε>0，?N，?m>n>N，成立
k=n+1
∑uk(a)<ε 与 ∑uk(b)<ε。
k=n+1
m
hd
∞n=1
aw
此即说明∑un(x)在[c,d]一致收敛，因此∑un(x)在[c,d]连续。由于
∞∞
.c
再由un(x)在[a,b]上的单调增加性，可知对一切x∈[a,b]，成立
m?m?
u(x)maxu(a),u(b)≤∑k∑k?<ε， ?∑kk=n+1k=n+1?k=n+1?m
此即说明∑un(x)在[a, b]上一致收敛。
n=1
∞
9. 设对一切n∈N，un (x)在x= a右连续，且∑un(x)在x = a发散，证明：对任意δ＞0，∑un(x)在(a, a +δ)上必定非一致收敛。
n=1∞
+
8
om
m
un+1(x)+un+2(x)+"+um(x)≤vn+1(x)+vn+2(x)+"+vm(x)<ε，
证 采用反证法。设∑un(x)在(a,a+δ)上一致收敛, 则
n=1
∞
?ε>0,?N,?m>n>N，?x∈(a,a+δ), 成立
m
k=n+1
∑uk(x)<
m
ε
2
。
再令x→a+,得到∑uk(a)≤
k=n+1
∞
ε
2
<ε, 这说明∑un(x)在x=a收敛，与条件
n=1
∞
矛盾，所以∑un(x)在(a, a +δ)上必定非一致收敛。
n=1
10．证明函数项级数∑ln??1+
n=2
∞
?
x?
其中a是?在[?a,a]上是一致收敛的，2
nlnn?
小于2ln22的任意固定正数。
答案
a
由于∑2收敛，所以
n=2nlnn
∞
∞
网 w
a?a?
～(n→∞)。 ln?1±±2?2
nlnn?nlnn?
n=2
∑ln?1±
∞
??
11．设
课
后
x??+ln1??在[?a,a]上一致收敛。 ∑2
?nlnn?n=2
x1
。 tannn2n=12
∞
f(x)=∑
π
（1） 证明：f(x)在[0,π/2]上连续； （2） 计算∫π2f(x)dx。
6
解 （1）对一切x∈[0,]，有
2
π
0≤
12
n
tan
x2
n
ww
≤12
n
a?
收敛，再由习题8可知2?nlnn?
9
.k
，
a?x?a????
， +≤+ln?1?ln1ln1≤????222?nnnnnnlnlnln??????
hd
aw
证 ln??1+
?x?
在[?a,a]上单调增加，所以 2?nlnn?
.c
om
∞1π1x
由于∑n收敛，由Weierstraass判别法，可知∑ntann在[0,]上一
22n=12n=12
∞
致收敛，从而f(x)=∑（2） 由（1），∑
∞
π1x
在[0,连续。 tannn
22n=12
∞
ππ1x
在[,上一致收敛，由逐项积分定理， tannn
622n=12
π
n+1∞n+1xx3?23?2n=1
， =ln∞∫π2f(x)dx=∫π2tan2nd2n=∑lnπn=1
66cosn+1∏cosn+1
22n=1
∞
π
cos
π
∏
∞
cos
π
n=1
6
n=1
n+n
x
3
（1） 证明：f(x)在(?∞,+∞)上连续；
课
证 （1）对一切x∈(?∞,+∞)，有
cosnxn+n
3
后
答
案
（2）记F(x)=∫0f(t)dt，证明：
由于∑
∞
网 w
12．设f(x)=∑
∞
cosnx
。
212?π??<F??<。 21522??
<1
3
n2
ww
，
∞
.k
dt=
∞
∫π2
hd
n=1n
π
ππ?sin?
?f(x)dx=ln?
?sin?
2?6
??
?=ln3。
2???
1
3n=1
n2
收敛，由Weierstraass判别法，可知∑
∞
aw
cosnx
n=1
.c
n+n
3
再利用例题9.5.3的结果∏cos
xsinx
，得到 =n
x2
一致收敛，所以f(x)=∑
n=1
cosnxn+n
3
在(?∞,+∞)上连续；
（2）由于∑
∞
cosnx
n=1
n+n
3
在(?∞,+∞)上一致收敛，由逐项积分定理，
F(x)=
∫0
x
f(t)dt=
n=1
∑∫0
∞
x
cosnt
n+n
3
∑
sinnx
n+n
3
10
om
在(?∞,+∞)上,
于是
nπ1?π?∞
F??=∑sin=
32?2?n=1nn+n
n=1(2n
∑
∞
(?1)n?1
?1)(2n?1)+(2n?1)
3
，
这是一个Leibniz级数, 它的前两项为
12
与?，所以 2330
21212?π?
?<?<F??<。 21523302?2?∞
1
13．设f(x)=∑n。
n=02+x
（1） 证明f(x)在[0,+∞)上可导，且一致连续；
敛；又
∞
f(x)=∑
由于
可知f(x)在[0,+∞)上一致连续。 （2） ∫0f(x)dx=∫0由于lim∑ln??1+
A→+∞
k=0n
课
∞∞111
f(x1)?f(x2)=∑n≤x1?x2?∑n， ?∑n
n=02+x1n=02+x2n=04
后
A
?
∫
+∞
f(x)dx发散。
11
答案
1
在[0,+∞)上可导。 n
n=02+x
∞
∞
A
nnA?1dxA?
(∑n)dx>∑∫0k=∑ln?1+k?，
2+xk=0?2?n=02+xk=0
∞
A
2kA?
?=+∞，可知lim∫0f(x)dx=+∞，所以反常积分A→+∞?
网
w
∞d1?1?
收敛，所以由逐项求导定理，∑2n∑?n?在[0,+∞)上一致收敛。
dx?2+x?n=02n=0
ww
.k
?11d?1??1
≤x∈，且对一切，，=[0,+∞)?n?n22nn2
dx?2+x?(2+x)(2+x)2
hd
aw
∞1∞111
≤n，∑n收敛，可知∑n证 （1）由n在[0,+∞)上点态收2+x2n=02n=02+x
.c
om
（2） 证明反常积分∫0f(x)dx发散。
+∞
习 题 10. 3 幂级数
1. 求下列幂级数的收敛半径与收敛域。
3n+(?2)nn
x; ⑴∑nn=1
∞
x2n
; ⑶∑(?1)n
n?2n=1
∞
n
1??1n
1"+++??(x?1); ⑵∑2n?n=1?∞
nln(n+1)(?1)(x+1)n； ⑷∑n+1n=1
∞
3n?x?1?
⑸∑?;
n=1n!?2?
∞
n
ln2nn2
⑹∑nn; n=2
∞
n!n
⑺∑n； n=1n
∞
(n!)2n
x; ⑻∑n(2)!n=1
∞
径为R=1。
课
∞
1??1n
（2）设∑?1++"+?(x?1)=∑an(x?1)n，liman=1，所以收敛半
n→∞n?2n=1n=1?
后
∞
答
案
?
所以收敛区域为D=?,??。 ?
11?当x=2时，∑an(x?1)=∑??1++"+?，级数发散。
n
n=1∞
n=1?∞
∞
网
w
∞∞121n
当x=?时，∑anx=∑[(?1)n+(n]，级数收敛。
33n=1n=1n
11
?33?
∞
ww
2?
∞∞121n
当x=时，∑anx=∑[1+(?n]，级数发散。
33n=1n=1n
11?
当x=0时，∑an(x?1)=∑(?1)n??1++"+?，通项不趋于零，级
n
n=1
n=1
.k
2
数也发散。
所以收敛区域为D=(0,2)。
52
hd
n?
∞3n+(?2)nn1
x=∑anxnliman=3，所以收敛半径为R=。解（1）设∑n→∞n3n=1n=1
∞
aw
n?
.c
(2n)!!n
。 ⑼∑
n=1(2n+1)!!
om
∞
∞x2n(?1)n1n2=axlima=（3）设∑(?1)，，所以收敛lim=∑nnnnn→∞→∞nn?2n2?2n=1n=1∞n
半径为R=2。 (?1)n当x=±2时，∑anx=∑，级数收敛。 n=1n=1n∞n∞
所以收敛区域为D=[?2,2]。
∞ln(n+1)n（4）设∑(?1)(x+1)=∑an(x+1)n，liman=1，所以收敛半n→∞n+1n=1n=1∞n
当x=0时，∑an(x+1)=∑(?1)n
n=1n=1n
当x=?2时，∑an(x+1)=∑n=1n
∞?an+13n?x?1?n!?2n?3n+1n=lim?（5）设∑?n?=0，?=∑an(x?1)，limn+1n→∞n→∞an3?n=1n=1n!?2??(n+1)!?2∞n
所以收敛半径为R=+∞, 收敛区域为D=(?∞,+∞)。
2ln2nn2∞2lnnn（6）设∑nx=∑anx，liman=limnn=1，所以收敛半径为n→∞n→∞nn=1n=2n
R=1。 课后∞
当x=±1时，显然∑anxn收敛，所以收敛区域为D=[?1,1]。
n=1
?(n+1)!nn?1an+1n!n∞n=lim?（7）设∑n=∑anx，lim??=，所以收敛半n+1n→∞→∞nan!?enn=1n=1n?(n+1)
径为R=e。
∞∞n!n当x=±e时，∑anx=∑n(±e)n，应用Stirling公式 n=1n=1n∞答案∞n!～2n
53网 wn+12e?nww(n→∞)， 所以收敛区域为D=(?2,0]。 .khd∞ln(n+1)，级数发散。 n+1n=1∞aw.c∞∞ln(n+1)是Leibniz级数，所以收敛。n+1om径为R=1 。
可知级数的通项
n!n
(±e)不趋于零，因而发散。 nn
所以收敛区域为D=(?e,e)。
∞
?[(n+1)!]2(2n)!?1an+1(n!)2n∞n
=lim?（8）设∑=∑anx，lim?=，所以收2→∞nn→∞+(2n)!a[2(1)]!n(!)nn=1n=1n??4
敛半径为R=4。
(n!)2
当x=±4时，∑anx=∑(±4)n，应用Stirling公式
n=1n=1(2n)!
∞
n
∞
n!～2n
n+
1
2e?n
(n→∞)，
以收敛半径为R=1。
∞
n
∞
当x=?1时，∑anx=∑(?1)n
n=1
n=1
当x=1时，∑anx=∑
n=1
∞
所以收敛区域为D=[?1,1)。
2. 设a＞b＞0，求下列幂级数的收敛域。
?anbn?n⑴∑??x; ?n+n2?
n=1??
∞
课
由Raabe判别法可知级数发散。
后
答
案
n
b(2n)!!(2n)!!1
，令bn=， limn(n?1)=，
n→∞(2n+1)!!bn+12 n=1(2n+1)!!
∞
网
w
ww
(2n)!!
是Leibniz级数，所以收敛。
(2n+1)!!
⑶ a x + b x2 + a2 x3 + b2 x4 + … + an x2n - 1 + bn x2n + …。
anbn?1
?=a，所以收敛半径为R=。 解（1）?+
n→∞?nan2???
∞
?anbn?n∞?(?1)nbn(?1)n1
+2nx=∑?+2?当x=?时，∑????nan?nan=1?n=1?n
.k
∞
a?(2n+2)!!(2n+1)!!?(2n)!!n∞
=∑anxn，limn+1=lim??=1，所（9）设∑?→∞nn→∞ann=1n=1(2n+1)!!?(2n+3)!!(2n)!!?
∞
xn
⑵∑an+bn;
n=1
hd
aw
?
?，级数收敛。 ??
所以收敛区域为D=(?4,4)。
54
.c
(n!)2
(±4)n不趋于零，因而发散。 可知级数的通项(2n)!
om
∞
?anbn?n∞?1bn1
+2nx=∑?+2?当x=时，∑????an?nan=1?nn=1?n?
?，级数发散。 ??
11?
所以收敛区域为D=??,?。 ?
?aa?
（2）limn→∞
11
=，所以收敛半径为R=a。 nn
aa+b
∞
xn
当x=±a时，∑nn的通项不趋于零，级数发散，所以收敛区
n=1a+b
域为D=(?a,a)。
（3）设a x + b x + a x + b x
2
2
3
2
4
.c
1a
+…+ an x2n - 1 + bn x2n + …=
n→∞n→∞
a,
n
n=1
为D=???
?
?1a
n
1?
??。 a?
∞
3. 设
∑a
n=0
∞
∞
x与∑bnxn的收敛半径分别为R1和R2, 讨论下列幂级数的
n=0
后
收敛半径：
n=0
∞
答案
网 w
ww
当x=±
1
，∑cnxn的通项不趋于零，级数发散，所以收敛区域
∞
.k
hd
limcn=lim2nan=a，所以收敛半径为R=
课
(1) ∑anx; (2)
2n
aw
∞n=0
。
∑(a
(3)
∑abx
nnn=0
∞n=0
n
。
解 （1）设∑anx2n的收敛半径为R。
当x<R1时，∑anx收敛，当x>R1时，∑anx2n发散，所以
2n
n=0
n=0
∞
∞
R=R1。
（2）设∑(an+bn)xn的收敛半径为R。
n=0
∞
55
om
n
n=1
∑cnxn，则
∞
+bn)xn;
当x<min(R1,R2)时，∑(an+bn)xn收敛。
n=0
∞
当x>min(R1,R2)，R1≠R2时，∑(an+bn)xn发散。
n=0
∞
但当R1=R2时，∑(an+bn)xn的收敛半径有可能增加，例如
n=0
∞
n=0
∑anx=
∞n=0
∞
n
n=0
∑x，收敛半径为1，∑bnx=
n=0
∞
n
∞
n
?1?n
?1?∑n?x收敛半径也为1，?n=0?2
∞
但∑(an+bn)xn的收敛半径为2。
所以R≥min(R1,R2)。
（3）设∑anbnxn的收敛半径为R。
n→∞
n→∞
n→∞
∞
n=0
n=0n=0
4. 应用逐项求导或逐项求积分等性质，求下列幂级数的和函数，并
指出它们的定义域。
⑴⑶⑸
n
网 w
；
n?1
答案
∑nx
n=1∞n=1∞
∞
ww
∑anx
∞
n
=
∑x
∞
2n+1
，收敛半径也为1，但∑anbnxn的收敛半径为R=+∞。
n=0
后
∑(?1)
n=1∞
nx；
2
nn
.k
∞
x2n
； ⑵∑2n+1n=0
∞
xn
； ⑷∑
n=1n(n+1)
∞
∑n(n+1)x
；
x2n
； ⑹1+∑n=1(2n)!
∞
课
n+1n
x。 ⑺∑n=1n!
∞
解 （1）级数∑nxn的收敛半径为R=1，当x=±1时，级数发散，所以
n=1
定义域为D=(?1,1)。
S(x)∞n?1
设S(x)=∑nx，f(x)==∑nx，利用逐项求积分，得到
xn=1n=1
n∞
56
hd
n=0
上式等号可能不成立，例如∑anx=∑x2n，收敛半径为1，
n
∞∞
aw
.c
由limanbn≤liman?limbn，可知R≥R1R2。
om
n=0
∫0
所以
x
f(x)dx=
n=1
∑∫0
∞
x
nx
n?1
dx=
n=1
∑xn
∞
=
x
， 1?x
S(x)=x
∞
d?x?x
。 ??=2
dx?1?x?(1?x)
x2n
的收敛半径为R=1，当x=±1时，级数发散，所以（2）级数∑n=02n+1
定义域为D=(?1,1)。
n=0
S(x)=
∞
n=1
所以定义域为D=(?1,1)。
后
分与上面习题（1），得到
课
设S(x)=∑(?1)
n=1
∞
答
案
（3）级数∑(?1)n?1n2xn的收敛半径为R=1，当x=±1时，级数发散，
n?1
S(x)∞
nx，f(x)==∑(?1)n?1n2xn?1，利用逐项求积
xn=1
2
n
∫0
所以
x
f(x)dx=
n=1
∑∫0(?1)
∞
网 w
1xdx11+x
。 =ln∫20
2x1?xx1?x
ww
dx=
∞n=1
.k
x
n?12
所以
hd
nx
n?1
∑(?1)n?1nxn=
d?x?x(1?x)?=S(x)=x?。 2??dx?(1+x)?(1+x)3
xn
的收敛半径为R=1，当x=±1时，级数收敛，所以（4）级数∑
n=1n(n+1)
∞
57
aw
x
， 2
(1+x)
f'(x)=
∑x2n=
∞
1
， 2
1?x
.c
om
x2n
，f(x)=xS(x)=设S(x)=∑2n+1n=0
∞x2n+1
，利用逐项求导，得到 ∑2n+1n=0
∞
定义域为D=[?1,1]。
xn
，f(x)=xS(x)=设S(x)=∑
n=1n(n+1)
∞
xn+1
，利用逐项求导，得到∑
n=1n(n+1)
∞
f"(x)=
x
n=1
∑xn?1=
∞
1
， 1?x
于是f'(x)=∫0=?ln(1?x)，所以
1?x
S(x)=
dx
1x1
f'(x)dx=1?(1?ln(1?x)，x∈[?1,1)， ∫0xx
而S(1)=∑
x→1?
n=1
以定义域为D=(?1,1)。
答案
与上面习题（1），得到
后
∫0
所以
x
f(x)dx=
n=1
∑∫0
∞
网
w
S(x)∞
设S(x)=∑n(n+1)x，f(x)==∑n(n+1)xn?1，利用逐项求积分
xn=1n=1
n
∞
ww
∞n=1
.k
n?1
x
n(n+1)x
dx=∑(n+1)xn=
课
?d?12x
??=?1S(x)=x??(1?x)3。 dx?(1?x)2?
x2n
的收敛半径为R=+∞，所以定义域为D=(?∞,+∞)。（6）级数1+∑n=1(2n)!
∞
∞x2nx2n?1
，则S'(x)=∑，由S(x)+S'(x)=ex与 设S(x)=1+∑n=1(2n)!n=1(2n?1)!
∞
S(x)?S'(x)=e?x，即可得到
58
hd
（5）级数∑n(n+1)xn的收敛半径为R=1，当x=±1时，级数发散，所
∞
aw
1
?1， 2
(1?x)
.c
限S(1)=limS(x)=1得到。
om
1
=1。注意S(1)也可利用S(x)在[?1,1]上的连续性，由极(1)nn+n=1
∞
S(x)=
1x
(e+e?x)。 2
（7）级数∑
n+1n
x的收敛半径为R=+∞，所以定义域为D=(?∞,+∞)。n=1n!
∞
∞
∞xn+1xn+1n
设S(x)=∑=x(ex?1)，所以 x，则∫0S(x)dx=∑
n=1n!n=1n!
S(x)=
d
x(ex?1)=(1+x)ex?1。 dx
[]
注 本题也可直接利用例题10.3.6，得到
∞xn?1n+1n
+S(x)=∑x=x∑?(n1)!n!n=1n=1
∞
om
1n
∑x=(1+x)ex?1。 n=1n!
∞
n=0n=0
在x = r收敛，就成立
并由此证明：
n=0
到
课
后
所以∑anxn的收敛半径也至少为r。当x∈[0,r)， 利用逐项积分，得
∞
答案
∞
ann+1a
可知∑nxn+1的收敛半径至少为r， 证 由于∑x在x = r收敛，
nn+1+1n=0n=0
∞
∫0
∞
x
f(x)dx=
∞aann+1
由于∑收敛, 可知∑nn+1在[0,r]连续, 令x→r?，得到
n=0n+1n=0n+1
∫0
对f(x)=ln
1
x
r
f(x)dx=
1
利用上述结果，就得到 1?x
59
网 w
∫
10
1dx∞1
=∑2。 ?ln
1?xxn=1n
ann+1
x。 n=0n+1
∑
∞
ann+1
r。 n+1n=0
∑
∞
ww
.k
∫
r0
f(x)dx = ∑
ann+1
r， n=0n+1
hd
∞
aw
.c
5. 设f (x) =
∑anx, 则不论∑anx在x = r是否收敛，只要∑
n
n
∞∞
ann+1
xn+1n=0
∞
1dxln∫01?x?x=
1
xn?1
∫0∑ndx=n=1
1∞∞1xn?1
dx=∑2。 ∑∫0nn=1n=1n∞
1
6. 证明：
x4n
满足方程 y (4) = y ; (1) y = ∑n=0(4n)!
∞
xn
(2) y = ∑满足方程 xy′′ + y ' - y = 0。 2
n=0(n!)
∞
证 （1）连续4次逐项求导，得到
y
(4)
∞x4nx4n?4
=∑=y。 =∑
n(4n?4)!(4)!n=1n=0
∞
（2）应用逐项求导，可得
于是
∞
答案
n; ⑴∑(?1)n2n=1
∞
n(n+2)⑶∑n+1;
4n=1
∞
1n
; ⑸∑(?1)n
3(2n+1)n=0
n?1
∞
网
w
ww
n
.k
∞
7. 应用幂级数性质求下列级数的和
⑵
(n+1)2
; ⑷∑n
2n=0
∞
hd
∞n=2
∞∞xnxn?1nxn?1
=∑=y。 xy"+y'=1+∑=1+∑22
n=2(n?1)!n!n=2[(n?1)!]n=0(n!)
1
; ∑n
n?2n=1
⑹
∑(?1)n
后
2n+1
。 ⑺∑(?1)n!n=0
∞
n
课
解 （1）设f(x)=∑(?1)
n=1
∞
n?1
f(x)∞
nx，令g(x)==∑(?1)n?1nxn?1，利用逐项
xn=1
求积分可得
g(x)=
1x
，于是 ， f(x)=22
(1+x)(1+x)
所以
n=1
∑(?1)n?1
∞
n12
。 =f=(n
292
60
aw
.c
1
;
2n(n2?1)
∞xn?1xn?2
，y"=∑， y'=∑
(n?1)!n!(n?2)!n!n=1n=2
∞
om
（2）设f(x)=∑xn，利用逐项求导可得
f(x)=ln1， 1?x1n=1n∞
所以
11=f(=ln2。 n2n=1n?2∑∞
（3）首先由逐项求积分可得∑nx
n=1∞n?1∞1n+1。设，f(x)=n(n+2)x=∑2(1?x)n=1
所以
（4）设f(x)=∑(n+1)2xn，利用逐项求积分可得
课后∞n=0答案11n(n+2)1。 =f(=n+14274n=1∑∞
∫0
于是 xf(x)dx=n=0∑(n+1)x∞网 www=n=1x2(3?x)， f(x)=(1?x)3n+1∑nxn=∞
f(x)=1+x， (1?x)3
所以
(n+1)21∑n=f(=12。 22n=0∞
61.kx， (1?x)2hd于是 aw∫0f(x)dx=∑nxn=1xn+2.c∞x3， =2(1?x)om再利用逐项求积分，得到
∞(?1)n(?1)n2n（5）设f(x)=∑x，令g(x)=xf(x)=∑x2n+1，利用逐项求
n=02n+1n=02n+1∞
导可得
g(x)=arctanx，
于是
f(x)=arctanx， x
所以
n=0
f(x)=
课所以 后
(?1)nn+1f(x)x，令g(x)=，则 （7）设f(x)=∑n!xn=0∞答案于是 1x1111， xln(1+x)dxx=(?ln(1+x)?x+∫x02x42n=2∑(?1)n∞11333=f(=?ln。 28422n(n2?1)
(?1)n
ng(x)=∑x=e?x， n!n=0∞
因此f(x)=xg(x)=xe?x。所以
2n+12(1)?。 =f(2)=∑2n!en=0∞n
62网 w(?1)nnx=g'(x)=∑n=2n?1∞(?1)n+1n+1x=xln(1+x)， ∑nn=1∞ww(?1)nn+1令g(x)=xf(x)=∑2x，则 n=2n?1∞.khdaw∞(?1)n(?1)n+1n（6）首先由逐项求导可得∑x=ln(1+x)。设f(x)=∑2xn，nn=1n=2n?1∞.com∑(?1)n∞113(=f=π。 n63(2n+1)3
∞
an
=0，8．设正项级数∑an发散，An=∑ak，且lim求幂级数anxn的∑n→∞Ak=1n=1n=1n
∞
n
收敛半径。
解 设幂级数∑anx的收敛半径为R1，∑Anxn的收敛半径为R2。由
n=1
n=1
∞
n
∞
0≤an≤An，可知R1≥R2；又由∑an发散，可知R1≤1。
n=1
∞
由于
lim
AnA?an+1
=limn+1=1， n→∞An+1An+1
n→∞
2nn11
证 （1）∑2x的收敛半径为R=，且在x=±，级数收敛，由Abel
22n=1n
∞
∞
2nn2nn11??11?
所以f(x)=∑2x在?第二定理，?,? ∑2x在??,?上一致收敛，?2222?n???n=1nn=1
∞
∞2nd?2nn?2nn?1??11n?1
?=δ>0由于?，且对任意，x在上 xδ,??x∑??2?22ndx?n??n=1?n?
2nn?111?
一致收敛，即∑x在??,?上内闭一致收敛，由函数项级数的逐?n22??n=1
∞
∞2n2nn?11?
项求导定理，f(x)=∑2x在??,?上可导，且f'(x)=∑xn?1。
?22?n=1nn=1n
∞
课
上连续。
（2）f(x)在x=处的左导数不存在。
2nn
令t=2x, 则f(x)=∑2x=
n=1n
∞
∞tntn
∑2。令g(x)=∑2。利用逐项求导 n=1nn=1n∞
63
后
1
2
答案
网 w
ww
2nn
9．设f(x)=∑2x。
n=1n
11??11?
（1） 证明f(x)在?上连续，在?,?上可导； ?,????22??22?
1
（2） f(x)在x=处的左导数是否存在？
2
∞
.k
hd
aw
.c
可知R2=1。结合上述关系, 得到R1=1。
om
定理，可以得到
g(t)=∫0?tln(1?u)du， u
其中t∈[?1,1]。应用L'Hospital法则，得到
1f(x)?f()=lim2?t?ln(1?u)du?1?ln(1?u)du? lim∫0∫0?11t→1?t?1?uu??x→?x?22
2tln(1?u)2ln(1?t)=lim?=?=+∞。 dulim∫t→1?t?11t→?1ut
64课后答案网
习 题 10. 4 函数的幂级数展开
1. 求下列函数在指定点的Taylor展开，并确定它们的收敛范围：
⑴1 + 2x-3x+ 5x ，x0 = 1; ⑶
x
， x0 = 0;
2?x?x2
2
3
1
⑵2， x0 = -1;
x
π
⑷sin x， x0 = ;
6
⑸ ln x ， x0 = 2;
x?1
， x0 = 1; x+1+x
， x0 = 0; ⑼ln
1?x
⑹
4?x2， x0 = 0;
⑺
⑻(1+x) ln (1-x), x0 = 0;
e?x
, x0 = 0。 ⑽1?x
=5+11t+12t2+5t3=5+11(x?1)+12(x?1)2+5(x?1)3。
级数的收敛半径为R=1。
（3）
xx1?12?
==???
2?x?x2(2+x)(1?x)3?1?x2+x?
1?∞n∞(?1)nn?1∞?(?1)n+1?n=?∑x?∑nx?=∑?1+?x。 n3?n=02n=02?3n=0??
级数的收敛半径为R=1。
当x=±1时，级数发散，所以收敛范围是D=(?1,1)。 （4） sinx=sin[(x?+=sincos(x?+cossin(x?)
6
6
6
6
6
6
课
当x=?2与x=0时，级数发散，所以收敛范围是D=(?2,0)。
后
答
案
∞∞1n?1
=∑n(x+1)=∑(n+1)(x+1)n。 2xn=1n=0
ππ
网
w
∞?11
（2）由==∑(x+1)n，应用逐项求导得到
x1?(x+1)n=0
π
ww
.k
π
因为级数只有有限项，所以收敛范围是D=(?∞,+∞)。
hd
aw
π
1
.c
π
1 + 2x-3x2 + 5x3 =1+2(t+1)?3(t+1)2+5(t+1)3
om
解（1）令x?1=t，则
1∞(?1)nπ2n∞(?1)nπ2n+1=∑x?+
(x?)。 ∑2n=0(2n)!62n=0(2n+1)!6
级数的收敛半径为R=+∞，所以收敛范围是D=(?∞,+∞)。
∞(?1)n+1x?2??n
（5） lnx=ln[2+(x?2)]=ln2+ln?1+x?2)。 ?=ln2+∑n
2??n=1n?2
级数的收敛半径为R=2。
(?1)n+1
当x=4时，级数为ln2+∑，收敛；当x=0时，级数为
nn=1
∞
（6）
级数的收敛半径为R=2。
??un3(n+1)?4?=limn?limn?1=>1， ???n→∞?3n?1?1?n→∞?u?3??n+1
课
由Raabe判别法，级数收敛。所以收敛范围是D=[?2,2]。
x?11
（7） =?
x+12
∞(?1)n?1x?1∞(?1)nx?1n
x?1)=∑(x?1)n。 =∑nnx?12n=022n=1
1+
2
级数的收敛半径为R=2。
当x=3与x=?1时，级数发散，所以收敛范围是D=(?1,3)。
∞1n11?
（8） (1+x)ln(1?x)=(1+x)∑(?x)=?x?∑?+?xn。 ?
nn?n=2?n?1n=1
∞
级数的收敛半径为R=1。
2
后
答案
网 w
?1??1?????
当x=±2时，级数为4∑(?1)n?3?，令un=(?1)n?3?，则
n=0?n??n?
????
∞
ww
.k
hd
1?2∞(?1)n?x????
4?x2=4????=4∑2n?3?x2n。
?2?n=02?n?
??
aw
.c
om
ln2+∑
?1
，发散。所以收敛范围是D=(0,4]。 n=1n
∞
当x=1时，级数发散；当x=?1时，级数收敛。所以收敛范围是
D=[?1,1)。
（9）
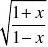
1
=[ln(1+x)?ln(1?x)] 2
1
2n+1。
n=02n+1
1∞?(?1)n?1n1n?=∑?x+x?=
n?2n=1?n
∑
∞
级数的收敛半径为R=1。
当x=±1时，级数发散，所以收敛范围是D=(?1,1)。
∞(?x)n∞∞?1e?x11(?1)nn
（10） =∑?∑x=1+∑??+?"+?1?xn=0n!n=0n!4!n=2?2!3!
设级数的xn项的系数为an，则
所以级数的收敛半径为R=1。
当x=±1时，级数的通项不趋于零，级数发散。所以收敛范围是
2. 求下列函数在x0 = 0的Taylor展开
课
后
x
至x4； ⑴
sinx
答案
D=(?1,1)。
网 w
ww
=
⑶ln cos x至 x6； 解 (1)
x=sinx
x
x?
1315x+x?"6120
1
?1214?1??x?x+"?
6120??
2
1414?1??1?
=1+?x2?x+"?+?x2?x+"?+"
120120?6??6?=1+
1274
x+x+"。 6360
111
=1+sinx+sin2x+sin3x+sin4x+"
2624
(2) esinx
3
.k
⑵esinx至x4； ⑷
1+x
至x4。 1?x
111
?<an< (n≥4)， 2!3!2!
hd
aw
.c
om
?n
?x。 ??
11?11????1?
=1+?x?x3+"?+?x?x3+"?+?x?x3+"?
666?6????2?1?111?
+?x?x3+"?+"=1+x+x2?x4+"。 24?628?
4
23
(3) lncosx=ln[1?(1?cosx)]=?(1?cosx)?(1?cosx)2?(1?cosx)3?"
141?11414??1?1?1?
x+"??" x+"???x2?=??x2?x+"???x2?
24243?224??2?2?2?1176
x?"。 =?x2?x4?
212240
2
3
1
213
3. 利用幂级数展开，计算下列积分，要求精确到0.001。
1sinx2
； dx ⑵∫0cosxdx； ⑴∫0
x1
+∞dxarctanx2。 dx； ⑷∫2⑶∫03
1+xx
n
1sinx1∞(?1)2n
解 (1)xdx=dx∑∫∫00xn=0(2n+1)!
n=0
设un=
1
，由于u3≈0.00003，因此前面4项之和的小数部
(2n+1)!(2n+1)
10
分具有三位有效数字，所以
课
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，
∫
(2)
3(?1)nsinx
≈ dx≈∑
xn=0(2n+1)!(2n+1)
2
后
=
∑
∞
∞(?1)n2n(?1)n
∫0(2n+1)!xdx=∑(2n+1)!(2n+1)，
n=0
1
∫
=
10
cosxdx=∫0
∞
n=0
∑∫0
1
∞(?1)n4n(?1)n
xdx=∑， (2n)!n=0(2n)!(4n+1)
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，设un=
1
，由于u3≈0.0001，因此前面4项之和的小数部分具
(2n)!(4n+1)
4
答案
1∞
(?1)n4n
xdx∑(2n)! n=0
网 w
ww
1
.k
hd
1115
?(x+x2+x3+")2+(x+x2+")3?(x+")4 2224
113
=1+x+x2+x3+x4+"。
228
aw
.c
om
(4)
1+x
=+2(x+x2+x3+x4+")=1+(x+x2+x3+x4+")1?x
有三位有效数字，所以
∫
(3) ∫
=
120
10
(?1)n
≈ cosxdx≈∑
(2n)!(4n+1)n=0
2
3
1
arctanx
dx=∫02x120
(?1)n2n
dx∑
n=02n+1
∞
n=0
∑∫
∞
∞(?1)n2n(?1)n1xdx=∑， ?221
2n+1+(2n1)2n=0
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，设un=
11
，由于u3≈0.00016，因此前面4项之和的小数部?22n+1
(2n+1)2
120
分具有三位有效数字，所以
=
n=1
具有三位有效数字，所以
∫
2
ex?1
4. 应用在x = 0的幂级数展开，证明：
x
∞
n
= 1。 ∑(n+1)!n=1
课
后
答案
+∞
4dx(?1)n?1≈∑≈ 33n?1
1+xn=1(3n?1)2
ex?11∞xn
证 ?1)==(∑
xn=0n!x
网
w
设un=
1
，由于u4≈0.00004，因此前面4项之和的小数部分3n?1
(3n?1)2
xn?1
=∑n=1n!
∞∞
应用逐项求导，得到
xex?ex+1
=2
x
nxn?1
， ∑(n+1)!n=1
以x=1代入，即得到
n
= 1。 ∑n=1(n+1)!
∞
5．求下列函数项级数的和函数
(?1)n?1?2+x?
（1）∑??
+?n(n1)2x??n=1
∞
2n
；
5
ww
∞
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，
.k
∑∫2
∞
+∞
∞(?1)n?1(?1)n?1
dx=∑， 3n3n?1
xn=1(3n?1)2
xn
, ∑
n=0(n+1)!
hd
aw
2
1??
x3?1+3?
x??
=∫2
.c
(4)
∫
+∞
dx+∞
=∫2
1+x3
dx
+∞∞
(?1)n?1∑3nn=1x
om
∫
3arctanx(?1)n1
dx≈∑≈ ?22n+1x2n=0(2n+1)
11?n
（2）∑??1++"+?x。
n=1
∞
?
2
n?
(?1)n?1n+1解 (1) 令f(t)=∑?t，应用逐项求导，得到
n=1n(n+1)
∞
f"(t)=
n=1
∑(?1)n?1tn?1=
∞
1
， 1+t
于是
f'(t)=ln(1+t)，f(t)=∫0ln(1+t)dt=(1+t)ln(1+t)?t，
t
从而得到
(2) 由级数乘法的Cauchy乘积，
课
后
其中x∈(?1,1)。
答案
?1
∑?1++"+
2n=1?
∞
1?n?∞n??∞xn
?x=?∑x??∑?n??n=0??n=1n
网 w
6．设{an}是等差数列，b>1，求级数∑解 设an=c+(n?1)d, n=1,2,"，则
∞
∞n?11
∑n=c∑n+d∑n。
n=2bn=1bn=1b
∞n?1∞1111
。设f(x)=∑nn?2，则 首先我们有∑n=?=
1b?1bn=2bn=1b1?b∞xn?1x1xx
=?fxdx()=， =∑∫02nxb(b?x)bbn=2
1?b
1
，所以 于是f(x)=2
(b?x)
an
∞
ww
6
(?1)n?1?2+x?
?∑+?nnx(1)2??n=1
∞
2n
2(x2+4)2(x2+4)
=ln?1, x∈(?∞,0]。 22
(x+2)(x?2)
.k
∞
?11
?=ln?1?x1?x, ?
an
的和。 n
n=1b
hd
2+x?
以t=???代入，得到
?2?x?
2
aw
.c
(?1)n?1n1
?t=(1+ln(1+t)?1，t∈[?1,1]。 ∑
tn=1n(n+1)
∞
om
n?11
=f(1)=。 ∑n2
(b?1)n=2b
∞
从而得到
n?1c(b?1)+d=。 ∑nn2n
(b?1)n=1bn=2bn=1b
1lnx
7．利用幂级数展开，计算∫0dx。
1?x2
∞
an
=c∑
∞
1
+d∑
∞
∞∞11lnx1∞2n2n
=?， 解 ∫0dx=(xlnx)dx=xlnxdx∑∑∫0∫220∑1?xn=0n=0n=0(2n+1)
1
1π21
，等式两边乘以，得到利用例题10.4.6中得到的结果∑2=64n=1n
∞
于是得到
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，设un=
4?11?
?2n?1+2n?1?，由于u7≈0.000038，因此前面7项之和的小2n?1?23?
数部分具有四位有效数字，所以
?4?11??
?2n?1+2n?1??≈3.1416。
3??n=1?2n?1?2
11∞(2n?1)!!1
(2) π=6arcsin=+∑?2n+1。
22n=1(2n)!!(2n+1)2
∞(2n?1)!!11∞1
设un=?2n+1，由于∑un<∑2n+1≈0.0000125，因此前面
(2n)!!(2n+1)213n=62n=6
7项之和的小数部分具有四位有效数字，所以
课
π≈∑(?1)n?1?
后
7
答案
8． (1) 应用= arctan+ arctan, 计算π的值，要求精确到10?4；
π11423π1
(2) 应用= arcsin, 计算π的值，要求精确到10?4。
62
∞?4?11??11
解 (1) π=4(arctan+ arctan)=∑(?1)n?1??2n?1+2n?1??。
233??n=1?2n?1?2
网 w
π2lnx
∫01?x2dx=?8。
1
ww
7
.k
hd
1π2
=， ∑2
8n=0(2n+1)
∞
aw
.c
1π2
=，两式相减，得到 ∑2
24n(2)n=1
∞
om
16(2n?1)!!11
π=6arcsin≈+∑?2n+1≈3.1416。
2n=1(2n)!!(2n+1)22
9．利用幂级数展开，计算∫1edx的值，要求精确到10?4。
n∞(?1)n3(?1)=∑∫1dx 解 ∫1edx=∫1∑nn
n!xn=0n!xn=0
∞(?1)n1??
=2?ln3+∑?1??。 n?1
3?n=2n!(n?1)?
3
?
3?
1x
1x
3∞
这是一个Leibniz级数，其误差不超过被舍去部分的第一项的绝对值，设un=
11??
?1?n?1?，由于u7<0.000033，因此前面8项之和的小数n!(n?1)?3?
部分具有四位有效数字，所以
课
后
答案
网 w
ww
8
.k
hd
aw
.c
om
(?1)n?1?
?+?2ln31edx≈??≈ ∑∫1n?1
3?n=2n!(n?1)?
3
?
1
x
7
习 题 10. 5 用多项式逼近连续函数
1. 求f (x) = x3的Bernstein多项式Bn(f , x)。
nk(k?1)(k?2)k3kkn?kkkn?k
解 Bn(f,x)=∑3nx(1?x)=∑x(1?x)+ n3
nk=3k=1n
n3k(k?1)nkkkn?kkkn?k
。 x(1?x)+x(1?x)∑∑n33n
nk=2k=1nkkkn!k?1
=?=Cn利用等式Cn?1，可分别得到 nnk!(n?k)!
nk(k?1)(k?2)n(n?1)(n?2)kkn?kk?3kn?k
x(1?x)=x(1?x)∑∑nn?332
nnk=3k=3
(n?1)(n?2)3(n?1)(n?2)3nk?3k?3n?k
x； =xCx(1?x)=∑n?322
nnk=3
n3k(k?1)n3(n?1)kkn?kk?2kn?k
x(1?x)=x(1?x)∑∑nn?232
nnk=2k=2
3(n?1)23(n?1)2nk?2k?2n?k=x； =xCx(1?x)∑n?222
nnk=2nkn1kkn?k?1kn?k
∑3nx(1?x)=∑2nk?1x(1?x)
k=1nk=1n
11nk?1k?1n?k
x。 ==2x∑Cnx(1?x)?12
nk=1n
n
所以
n
后
解 B4(f,x)=∑
3. 设f (x)在[a, b]上连续，证明：对任意给定的ε>0，，存在有理系数多项式P(x)，使得
P(x)?f(x)<ε。 对一切x∈[a, b]成立。
证 由定理10.5.1，对任意给定的ε>0，存在多项式Q(x)，使得对一切x∈[a,b] 成立
Q(x)?f(x)<
n
课
=2x(1?x)+32x2(1?x)2+23x3(1?x)+x4
=(32?2?1)x4+2(3+3?32)x3+3(2?2)x2+2x。
答案
(n?1)(n?2)33(n?1)21k3kk
x+x+2x。 Bn(f,x)=∑3nx(1?x)n?k=22
nnnk=1n
2. 设f (x) =x，x∈[0, 1]，求它的四次Bernstein多项式B4(f ,x)。
4
k=13
kkk
4x(1?x)4?k 4
网 w
由于有理数集合在设Q(x)=∑bkxk，其中bk(k=0,1,2,",n)是实数，
k=0
ww
ε
2
9
.k
。
hd
aw
.c
om
实数集中是稠密的，可以取有理数ak(k=0,1,2,",n)分别与
bk(k=0,1,2,",n)充分接近，令P(x)=
P(x)?Q(x)<
k=0
∑akxk，使得对一切x∈[a,b]成立
2
n
ε
。
于是
P(x)?f(x)≤P(x)?Q(x)+Q(x)?f(x)<ε
对一切x∈[a,b]成立。
4. 设f(x)在[a,b]上连续，且对任一多项式g(x)成立
∫
b
a
f(x)g(x)dx=0。
切x∈[a,b]成立
由于
2
∫a[f(x)?P(x)]dx=
b
b
网 w
ww
22
∫a[f(x)?2f(x)P(x)+P(x)]dx=
22
∫a[f(x)+P(x)]dx，
b
课
由ε的任意性，得到
2
∫af(x)dx=0，
b
再由f(x)的连续性，得到
f(x)≡0。
后
∫a
b
答案
所以
f2(x)dx≤
2222
<(b?a)ε[f(x)+P(x)]dx=[f(x)?P(x)]dx。 ∫a∫a
b
5. 设P0(x)=0，Pn+1(x) =Pn(x)+
x2?Pn2(x)
2
在[-1,1]上一致收敛于｜x｜。
x2?t2
证 首先有0≤P0(x)≤x。设0≤Pk(x)≤x，由于函数h(t)=t+在
2
10
.k
b
P(x)?f(x)<ε。
（n = 0,1,2,…），证明：｛Pn(x)｝
hd
aw
.c
证 由定理10.5.1，对任意给定的ε>0，存在多项式P(x)，使得对一
om
证明在[a,b]上成立f(x)≡0。
t∈[0,1]是单调增加的，所以有
x2?Pk2(x)≤x， 0≤Pk+1(x)=Pk(x)+2
由数学归纳法得到对一切自然数n成立 0≤Pn(x)≤x。 x2?Pn2(x)于是由Pn+1(x)=Pn(x)+，又得到Pn+1(x)≥Pn(x)，所以函数序列2
{Pn(x)}在[?1,1]上收敛。
2
11课后答案网 w ww{Pn(x)}在[?1,1]上是一致收敛于x的。 .khd得到P(x)=P(x)+x2?P2(x)，于是解得P(x)=x，并由Dini定理可知aw.cx2?Pn2(x)两边求极限，设limPn(x)=P(x)，对等式Pn+1(x)=Pn(x)+n→∞2om