陈纪修教授《数学分析》九讲学习笔记与心得

陈纪修教授《数学分析》九讲学习笔记与心得

云南分中心 ? 昆明学院 ? 周兴伟

此次听陈教授的课，收益颇多。陈教授的这些讲座，不仅是在教我们如何处理《数学分析》中一些教学重点和教学难点，更是几堂非常出色的示范课。我们不妨来温习一下。

第一讲、微积分思想产生与发展的历史

法国著名的数学家H.庞加莱说过：“如果我们想要预见数学的将来，适当的途径是研究这门科学的历史和现状。” 那么，如果你要学好并用好《数学分析》，那么，掌故微积分思想产生与发展的历史是非常必要的。陈教授就是以这一专题开讲的。

在学校中，我不仅讲授《数学分析》，也讲授《数学史》，所以我非常赞同陈教授在教学中渗透数学史的想法，这应该也是提高学生数学素养的有效途径。

在这一讲中，陈教授脉络清晰，分析精当，这是我自叹不如的。讲《数学史》也有些年头，但仅满足于史料的堆砌，没有对一些精彩例子加以剖析。如陈教授对祖暅是如何用 “祖暅原理”求出球的体积的分析，这不仅对提高学生的学习兴趣是有益的（以疑激趣、以奇激趣），而且有利于提高学生的民族自豪感（陈教授也提到了这一点）。

在这一讲中，陈教授对weierstrass的“ε?N”、“ε?δ”语言的评述是“它实现了静态语言对动态极限过程的刻画”。这句话是非常精当的，如果意识不到这一点，你就很难理解这一点。在此我还想明确一点：《数学分析》的研究对象是函数，主要是研究其分析性质，即连续性、可微性及可积性，而使用的工具就是极限。如果仔细盘点一下，在《数学分析》中，无论是数、函数、数列、函数列，数项级数，函数项级数等相关问题，无不用到这一语言，你应该能理解陈教授的“对于数学类学生来说，没有“ε?N”、“ε?δ”语言，在《数学分析》中几乎是寸步难行的”这一观点。

云南分中心 ? 昆明学院 ? 周兴伟

第二讲、实数系的基本定理

在这一讲中，陈教授从《实变函数》中对集合基数的讨论展开，对实数系的连续性作了有趣的讨论。首先是从绅士开party的礼帽问题，带我们走进了“无穷的世界”。

我在开《数学赏析》时有一个专题就是“无穷的世界”，我给学生讲礼帽问题、也讲希尔伯特无穷旅馆问题，但遗憾的是，当我剖析“若无穷旅馆住满了人，再来两个时，可将住１号房间的移往３号房间，住２号房间的移往４号房间，从而空出两个房间”时，学生对我“能移”表示怀疑。这一点我往往只能遗憾的说“跳不出有限的圈子，用有限的眼光来看无限，只能是‘只在此山中，云深不知处’”。当然，我还是会进一步考虑如何来讲好这一讲。若陈教授或其他老师有好的建议，能指点一下，则不胜感激。

对于集合[0,1]与(0,1)的对等关系，包括Q与Ｒ的对等关系，或者说他们之间双射的构造。关键在于“求同存异”，找一个可数集来“填补”他们之间的差距，这相当于希尔伯特无穷旅馆问题中来了两个人和来了可数个人。

对于实数集中的有理数，“廖若晨星”是非常形象的描述。一声集合的哨响，我们发现，有理数在实数轴上几乎是没有位置的（mQ=0），用一系列的帽子来盖住这些点，而这些帽子的大小是ε，这是非常精彩的结果。

从可数集到不可数集，再加上无最大基数定理，让我们看到了“无穷的层次性”，由此我们不难理解“人外有人，天外有天，无穷之外有无穷”。我们不能不发出“哀吾生之须臾，羡长江之无穷”的感慨。

陈教授对单调确界原理的证明非常清晰明了，几何直观的描述形象直观。

第三讲 《数学分析》课程中最重要的两个常数

法国著名雕塑家罗丹曾经说过“生活中从不缺少美，而是缺少发现美的眼睛”。我想说：“数学中并不缺少美，缺少的是揭示数学美的老师”。陈教授是一个出色的老师，他不仅发现了数学的美，而且为我们展示了数学的美。

著名的欧拉公式：e?i?1?0，实现了有理数、无理数、超越数、实数、虚数

陈纪修教授《数学分析》九讲学习笔记与心得

完美统一，获得“最美的数学定理”称号。欧拉建立了在他那个时代，数学中最重要的几个常数（0,1,i,e,?）之间的绝妙的有趣的联系，被认为是数学奇异美的典例。

在本讲中，陈教授以李大潜院士访问法国“引入”的一个有趣例子开讲，让我们体会了数学中的美，这个不等式还有许多有意思的地方，无论是不等式的形式，还是他的证明，都非常深刻地体现了数学的美。Pi是无理数的证明，吸引了与会学员的眼球，赞叹之余，有学员问这一证法的出处，我也还真想知道，请陈教授不吝指教。

本讲最后将函数sinx/x展成无穷乘积形式，并妙用此形式求出p级数中p为偶数值时的和，对我而言是耳目一新的。在我记忆中好像菲尔金哥尔茨的《微积分学教程》(第二卷)中也有求出的方法，而p为奇数的情形好像至今尚未解决。对p=2的情形，欧拉至少用两种方法得到结果，其中一种方法妙用了L’Hospital法则(《数学译林》09.3)。

第四讲 级数与反常积分收敛的A.D判别法

恰逢这个学期讲《数学分析》(3)，在讲授含参变量反常积分时，先复习了反常积分，再复习了函数项级数，并将几个判别法列表比较，尤其是A.D判别法，能与陈教授不谋而合，真是倍感荣幸。

陈教授对Abel引理的直观刻画，也是深得学员好评。我对陈教授从Abel引理分析?anbn收敛条件的分析而得到Dilichlet判别法和Abel判别法的相关条件深感佩服，尤其是分析得丝丝入扣。

第五讲 函数项级数与含参变量反常积分的一致收敛

一致收敛性无疑是《数学分析》中的一个重要概念。陈教授对“点点收敛”与“一致收敛”的剖析是非常到位的，学生在学习时如果是只能注意到在定义的陈述“?x”的位置不相同，而不明其所以时，这样的教学肯定是失败的。陈教授例子选择精当，语言使用精辟，问题分析精准。

请注意陈教授的这句话：“毛病出在点态收敛的情况下，在某些点附近，N无法控制”（类似的话在第九讲中说过）。

云南分中心 ? 昆明学院 ? 周兴伟

第六讲 Weierstrass函数：处处连续处处不可导的函数

陈教授分析了为何在Weierstrass之前的数学家不能构造出这样的函数。原来在此之前，数学家们所掌握的函数是不足以构造出这样的函数的。

Weierstrass在1872年构造出了如下处处连续处处不可导的函数：

?ansin(bnx) 0<a<1<b, ab>1

陈教授选用19xx年Van Der Waerden给出的例子进行了剖析。所讲自是精当，本人很是受益。

第七讲 条件极值问题与Lagrange乘数法

本讲陈教授从一个几何问题入手，得到一个条件极值问题。考虑了条件极值的必要条件，引入Lagrange乘数法，化条件极值问题为无极条件极值问题。这部分内容中，本人认为几何解释最有启发性。

对于具体使用Lagrange乘数法的例子中，如何解方程组，陈教授给了很好的建议。第二个例子，即求平面x+y+z=0与椭球面x2+y2+4z2=1相交而成的椭圆面积。这个例子我很喜欢，只可惜不能用来做期末考题（不要问我为什么！）。

第八讲 重积分的变量代换

本讲陈教授从定积分的换元的计算公式分析入手，对二重积分的相应的代换公式作出类比猜想（在教学中注重渗透数学思想方法，如此妙哉！）再作分析，然后得出代换公式。

为证明代换公式，陈教授引入本原映射，化“矩形”为“梯形”，化变换T为两个本原变换的复合，实现了化复杂为简单，化困难为容易。

第九讲 《数学分析》课程中的否定命题

《数学分析》教学中，说说“反话”很重要！（请不要误解！）

两个命题A与B如果既不能同时成立，也不能同时不成立，就称A与B互为否定命题。

陈纪修教授《数学分析》九讲学习笔记与心得

若A与B互为否定命题，则A与B一定满足：一个成立，另一个必然不成立；一个不成立，另一个必定成立。（废话！）

有界与无界、收敛于a与不收敛于a、收敛与不收敛、（注意前边两对的区别！）、可导与不可导、Cauchy收敛准则及其否定命题，等等。这些“反话”不说，大量的题做不了。

我在讲《数学分析》(1)时会有一讲（几个概念的否定叙述）就是来讲否定命题的。

陈教授在这部分的例子非常好，分析得也清楚！

陈教授的九讲，给了我们太多的启示：

一、在我们的教学中，不仅要教其所以然，而且要教其所以然。陈教授的这九讲，

应该是我们讲授《数学分析》的经典案例，当然，我们不一定是讲这一些内容！正确的思想从哪里来，是从天上掉下来的吗？不是！

二、在我们的教学，不仅要传授知识，而且要传授思想方法，也就是教学中要注

重思想方法的渗透。

三、在我们的教学中，不仅要传授知识，而且要培养学生的数学素养，让他们了

解数学的过去、现在，以便开创数学的将来。

四、在我们的教学中，或许会遇的许多困难：教学时数少，教学对象差等等，但

我们应从我们自身积极的寻找对策。陈教授就是这样的。

以上所述，仅凭个人听课记录，又仅凭个人理解。若是有误，请陈教授见谅并斧正。

最后，向陈纪修教授致以崇高的敬意！

滇源后学：周兴伟

第二篇：数学分析课后习题答案--高教第二版(陈纪修)--3章

课后答案网 www

第三章 函数极限与连续函数

习 题 3.1 函数极限

1. 按函数极限的定义证明：

x3＝8； ⑴limx→2

x?11

＝ ； x+12lnx=?∞； ⑸xlim→0+

x = 2； ⑵limx→4

x+11

= ； 2x?12e?x＝0； ⑹xlim→+∞

⑶lim

x→3⑷lim

x→∞

x→2

.k

limx3＝8。

hd

x?4

≤

1

x?4，于是2

x3?8<19x?2<ε，所以

（2）首先函数x的定义域为x≥0，且x?2=

1

x?4<ε，所以 2

limx= 2。

答

案

x?2≤

x→4

网

x+2

对任意的ε>0，取δ=min{4,2ε}>0，当0<x?4<δ时，成立

（3）先取x?3<1，则2<x<4，

意的ε>0，取δ=min{1,6ε}>0，当0<x?3<δ时，成立

x?111

?<x?3<ε，所以 x+126

x?11lim＝。 x→3x+12

33x+11

≤（4）先取x>1，则2x?1≥x，，于是对任意?=

2x?1222x?12x

课

后

的ε>0，取X=max??1,所以

3x+113?

<ε，?≤?>0，当x>X时，成立

x?22xε212??

lim

x→∞

w

x+11

=。 2x?12

34

ww

x?11x?31

?=<x?3，于是对任x+122(x+1)6

aw

于是对任意的ε>0，取δ=min??1,

?>0，当0<x?2<δ时，成立 19??

ε?

.c

om

x2 ⑻lim=?∞。

x→?∞x+1

证 （1）先取x?2<1，则1<x<3，x3?8=(x2+2x+4)(x?2)<19x?2，

2x

=+∞； ⑺xlim2

→2+x?4

（5）对任意的G>0，取δ=e?G>0，当0<x<δ时，成立lnx<?G，所以

limlnx=?∞。

x→0+

取X=ln>0，当x>X时，成立0<e?x<elnε=ε，（6）对任意的0<ε<1，

ε

1

所以

x→+∞

lime?x＝0。

（7）先取0<x?2<1，则2<x<3，

2x

>1，于是对任意的G>0，取 x+2

2x2x1?1?

=>>G，δ=min?1,?，当0<x?2<δ时，成立2

G(x+2)(x?2)x?2x?4??

所以

x→2+

lim

（8）先取x<?1，则

x→1

案

网

⑴lim⑶lim

x→0

x→0

课

后

⑸lim⑺limx→a⑼lim

x→0

解

x2?1

；

2x2?x?13x5?5x3+2x

；

x5?x3+3x(1+x)n?1

； x

sinx?sina

；

x?a

cosx?cos3x

； x2

w

2. 求下列函数极限：

ww

35

x2

当x<?X时，成立<x<?G，所以

x+1

x2

lim=?∞。 x→?∞x+1

答

x2?1x+12

=lim（1）lim2=。 x→12x?x?1x→12x+13

x2?11

=。 （2）lim2

x→∞2x?x?12

3x5?5x3+2x2?5x2+3x42

=lim=。 （3）lim53

24x→0x→0x?x+3x33?x+x

(1+2x)(1+3x)?1(1+5x+6x2)?1

（4）lim=lim=5。 x→0x→0xx

.k

⑵⑷⑹⑻⑽

x2?1

lim； 2

x→∞2x?x?1

(1+2x)(1+3x)?1lim； x→0x

(1+mx)n?(1+nx)mlim； 2x→0x

2xlim； x→01?cosx

tanx?sinxlim。 x→0x3

hd

aw

x

1,G}，>1，于是对任意的G>0，取X=max{

x+1

.c

2x

=+∞。 x2?4

om

3. 利用夹逼法求极限：

w

?1?limx⑴x→0??；

?x?

ww

.k

122Cnx+Cnx+?+xn(1+x)n?1

（5）lim=lim=n。 x→0x→0xx

(1+mx)n?(1+nx)m

（6）lim 2x→0x

222222

(1+nmx+Cnmx+?+mnxn)?(1+mnx+Cmnx+?+nmxm)=lim 2x→0x1

=nm(n?m)。 2

x+ax?a2cossin

sinx?sina=cosa。 （7）lim=limx→ax→ax?ax?a

x2x2

=2。 （8）lim=lim

x→01?cosxx→0?x?

2sin2??

?2?

cosx?cos3x2sin4xsin2x

==4。 （9）limlim22x→0x→0xx

?x?

2sinxsin2??

tanx?sinx?2?=1。 =（10）limlimx→0x→02x3cosxx3

hd

x→+∞

⑵limx。

nn11?1?

<x??≤1。由lim=1，可知 <x≤，有

n→∞n+1nn+1x+1n??

n+11?n+111?1?

limx??=1。?x<0，当?<x≤?，有1≤x?。由lim=1，<??x→0+?x?n→∞nnn+1n?x?

1?

可知limx?=1。由此得到 ?x→0??x??

?1?

limx??=1。 x→0?x?

课

后

答

案

网

解（1）?x>0，当

aw

1x

.c

om

（2）当n≤x<n+1，有n得到

1n+1

<x<(n+1)。由lim

1

xx

1x1n

n→∞

1nn+1

=1与lim

n→∞

1

(n+1)n

=1，

x→+∞

lim

=1。

4. 利用夹逼法证明：

xk

(1) limx = 0 (a＞1，k为任意正整数)；

x→+∞a

lnkx

(2) lim = 0 (k为任意正整数)。

x→+∞x

36

xk([x]+1)k(n+1)k

=0即得到 解（1）首先有0<x<，由lim[x]nn→∞aaa

xk

limx = 0。 x→+∞a

lnkxtk

=t，且当x→+∞时，有t→+∞。再利用（1）（2）令lnx=t，则xe

的结论，即得到

lnkxlim = 0。 x→+∞x

5. 讨论单侧极限：

?1?2x,0<x≤1,

2 (1) f(x)= ??x,1<x<2,

?2x2<x<3,?? 在x = 0,1,2三点；

(2) f(x) =

x→0?

课（3）D(x)在任意点无单侧极限。 （4）limf(x)=0，limf(x)=1。 11后x→n

6. 说明下列函数极限的情况：

(1) limx→∞sinx; (2) limexsinx; x→∞x

x211?α (3) limxsin; (4) lim??1+?; x→+∞x→∞xx??

?1?1??1??????; (6) lim。 (5) lim?+1???2?x→∞x→0+x???x?x??

sinx解（1）lim=0。 x→∞x

（2）limexsinx=0，limexsinx极限不存在，所以limexsinx极限不x→?∞x→+∞x→∞存在。

37答?1,x为有理数,D (x) = ? 在任意点； x为无理数0,,?11?1?。 (4) f(x) = ??, 在 x = （n=1,2,3,?）nx?x?1解（1）limf(x)=+∞，limf(x)=，limf(x)=1，limf(x)=4，limf(x)=4。 x→0+x→2?x→2+x→1?2x→1+（2）limf(x)=?1，limf(x)=1。 x→nx案x→0+网 www.k (3) Dirichlet函数 hd2?11x， 在x = 0点； aw2+11x.com

α<1?01?α=1。 （3）limxαsin=?1x→+∞x??+∞α>1

1??1??1?（4）lim??1+?=+∞，lim?1+?=0，所以lim?1+?极限不存x→+∞x2x2x2?x?x→?∞?x?x→∞?x?

在。

1?（5）lim?1+2?=1。 ?x→∞x??x

（6）取'xn1"=，xn=n?1?1???1?1??1????"?=，，则lim?'??'??=0，lim?"??2n→∞xn→∞x1xx????nnnn????????n+21

????1??x+2esinx?解 由于limf(x)=lim?+=0+1=1， 4?x→0+x→0+?1?x????ex?+1??????????

1???2+exsinx?limf(x)=lim?+?=2?1=1，所以 4x→0?x→0???x?x?1+e?

1???2+exsinx?+limf(x)=lim??=1。 4x→0x→0?|x|?x?1+e?

A 。 8. 设limf(x) = A（a≥0），证明：f(x2) = x→a课后答案网 w

证 设limf(x) = A（a≥0），则?ε>0，?δ'>0，?x(0<x?a<δ')，有 x→a

?δ'?f(x)?A<ε。取δ=min?1,?>0，则当0<x?a<δ时，首先有?1+2a?

x+a<1+2a，于是0<x2?a=(x+a)(x?)<δ'，从而f(x2)?A<ε，这就说明了f(x2) = A 。 x→a

9. (1) 设limf(x3) = A，证明：limf(x) = A 。 x→0x→0

38wwx→.k问当x→0时，f(x)的极限是否存在？ hd1???2+exsinx?+f(x)=??。 4|x|??1+ex??aw.c????所以lim??极限不存在。 ??x→0+?xx????7．设函数 ?11?om

(2) 设limf(x2) = A，问是否成立limf(x) = A？ x→0x→0证 （1）设limf(x3) = A，则?ε>0，?δ'>0，?x(0<x<δ')（即x→0

0<x3<δ'3），有f(x3)?A<ε。取δ=δ'3>0，则当0<x<δ时，有0<1

x3<δ'，从而f(x)?A<ε，这就说明了limf(x)= A 。 x→0

（2）当limf(x2)= A时，不一定成立limf(x)= A。例如：f(x)=?x→0x→0?1x>0，?0x<0则limf(x2)=1，但极限limf(x)不存在。 x→0x→0

课的数列{xn}(xn>x0)，成立

n→∞后（6）?G0>0,?X>0,?x∈(X,+∞):f(x)≥?G0。 11. 证明xlimf(x)=+∞的充分必要条件是：对于任意从右方收敛于x0→x+答案（4）?G0>0,?δ>0,?x∈(x0?δ,x0):f(x)≤G0。 （5）?ε0>0,?X>0,?x∈(?∞,?X):f(x)?A≥ε0。

证 必要性：由limf(x)=+∞，可知?G>0，?δ>0，?x(0<x?x0<δ)：x→x+0

f(x)>G。因为数列{xn}(xn>x0)收敛于x0，对于上述δ>0，?N，?n>N：0<xn?x0<δ。于是当n>N时，成立f(xn)>G，即n→∞limf(xn)=+∞。

0充分性：用反证法。设limf(x)=+∞不成立，则?G0>0，?δ>0，x→x+

1，n=1,2,3,?： n

对于δ1=1，?x1(0<x1?x0<1)：f(x1)≤G0； ?x(0<x?x0<δ)：f(x)≤G0。取δn= 网limf(xn)=+∞。 w（2）?G0>0,?N,?n>N:xn≤G0。 （3）?ε0>0,?δ>0,?x∈(x0,x0+δ):f(x)?A≥ε0。 ww39.k10. 写出下述命题的“否定命题”的分析表述： (1) {xn}是无穷小量； (2) {xn}是正无穷大量； (3) f(x)在x0的右极限是A； (4) f(x)在x0的左极限是正无穷大量； (5) 当x →?∞, f(x)的极限是A； (6) 当x→+∞，f(x)是负无穷大量。 解（1）?ε0>0,?N,?n>N:xn≥ε0。 hdaw.com

对于δ2=，?x2(0<x2?x0<)：f(x2)≤G0；

?,

1212

对于δk=

?,

11

，?xk(0<xk?x0<：f(xk)≤G0； kk

于是得到数列{xn}(xn>x0)收敛于x0，但相应的函数值数列{f(xn)}不

可能是无穷大量，由此产生矛盾，所以limf(x)=+∞成立。

x→x0+

12. 证明limf(x)=?∞的充分必要条件是：对于任意正无穷大量{xn},

x→+∞

成立

n→∞

limf(xn)=?∞。

大量{xn}，相应的函数值数列{f(xn)}收敛。 证 必要性：设limf(x)=A，则?ε>0，?X>0，?x>X：|f(x)?A|<ε。

x→+∞因为数列{xn}是正无穷大量，对于上述X>0，?N，?n>N：xn>X。于是当n>N时，成立|f(xn)?A|<ε，即limf(xn)=A。

n→∞

充分性：因为对于任意正无穷大量{xn}，相应的函数值数列 {f(xn)}收敛，我们可以断言{f(xn)}收敛于同一个极限。如果存在正无穷大量{x'n}与{x"n}，使得limf(x'n)=A，limf(x"n)=B，且A≠B，

n→∞

n→∞

则取x2n?1=x'n，x2n=x"n，{xn}仍然是正无穷大量，但相应的函数值数列{f(xn)}不收敛。

设{f(xn)}都收敛于同一个极限A，现用反证法证明limf(x)=A。

x→+∞

课

13. 证明limf(x)存在而且有限的充分必要条件是：对于任意正无穷

x→+∞

后

对于X1=1，?x1>1：f(x1)≥?G0； 对于X2=2，?x2>2：f(x2)≥?G0； ?,

对于Xk=k，?xk>k：f(xk)≥?G0； ?,

于是得到数列{xn}为正无穷大量，但相应的函数值数列{f(xn)}不可能是负无穷大量，由此产生矛盾，所以limf(x)=?∞成立。

答

案

网

w

ww

40

.k

x→+∞

f(x)≥?G0。取Xn=n，n=1,2,3,?：

hd

?X>0，?x>X：充分性：用反证法。设limf(x)=?∞不成立，则?G0>0，

x→+∞

aw

因为数列{xn}是正无穷大量，对于上述X>0，?N，?n>N：xn>X。

于是当n>N时，成立f(xn)<?G，即limf(xn)=?∞。

n→∞

.c

om

?X>0，?x>X：f(x)<?G。证 必要性：由limf(x)=?∞，可知?G>0，

x→+∞

设limf(x)=A不成立，则?ε0>0，?X>0，?x>X：|f(x)?A|≥ε0。x→+∞

取Xn=n，n=1,2,3,?：

对于X1=1，?x1>1：|f(x1)?A|≥ε0； 对于X2=2，?x2>2：|f(x2)?A|≥ε0； ?,

对于Xk=k，?xk>k：|f(xk)?A|≥ε0； ?,

于是得到数列{xn}为正无穷大量，但相应的函数值数列{f(xn)}不收敛于A，由此产生矛盾，所以limf(x)=A。

x→+∞

x→x0x→x0+

x→?∞

解 （1）极限limf(x)存在而且有限的充分必要条件是：对于任意给

x→x

f(x')?f(x")<ε。

ww

ε

.k

ε

先证必要性。设xlimf(x)=A，则?ε>0，?δ>0， →x

hd

aw

n→∞n→∞

定的ε>0，存在δ>0，对一切x',x"∈{x0<x?x0<δ}，成立

（2）xlimf(x)存在而且有限的充分必要条件是：对于任意给定的→x+

ε>0，存在δ>0，对一切x',x"∈{x0<x?x0<δ}，成立f(x')?f(x")<ε。

先证必要性。设xlimf(x)=A，则?ε>0，?δ>0， →x+

课

再根据相应的Heine定理，可知limf(x)存在而且有限。

x→x

后

f(xm)?f(xn)<ε。这说明函数值数列{f(xn)}是基本数列，因而收敛。

答

的δ>0，?N，?n>N：0<xn?x0<δ。于是当m>n>N时，成立

案

再证充分性。任意选取数列{xn}，xn≠x0，limxn=x0，则对于条件中

网

w

?x',x"∈{x0<|x?x0|<δ

22

|f(x')?f(x")|≤|f(x')?A|+|f(x")?A|<ε。

}：|

f(x')?A|<

，|f(x")?A|<。于是

?x',x"∈{x0<x?x0<δ

22

|f(x')?f(x")|≤|f(x')?A|+|f(x")?A|<ε。

}：|

f(x')?A|<

，|f(x")?A|<。于是

再证充分性。任意选取数列{xn}，xn>x0，limxn=x0，则对于条件中的δ>0，?N，?n>N：0<xn?x0<δ。于是当m>n>N时，成立f(xm)?f(xn)<ε。这说明函数值数列{f(xn)}是基本数列，因而收敛。再根据相应的Heine定理，可知xlimf(x)存在而且有限。 →x+

41

.c

εε

om

14．分别写出下述函数极限存在而且有限的Cauchy收敛原理，并加

以证明：

（1）limf(x)；（2）limf(x)；（3）limf(x)。

（3）limf(x)存在而且有限的充分必要条件是：对于任意给定的ε>0，

x→?∞存在X>0，对一切x',x"<?X，成立f(x')?f(x")<ε。

先证必要性。设limf(x)=A，则?ε>0，?X>0，?x',x"<?X：

x→?∞

|f(x')?A|<

ε

22

|f(x')?f(x")|≤|f(x')?A|+|f(x")?A|<ε。

n→∞

，|f(x")?A|<。于是

ε

则对于条件中的X>0，再证充分性。任意选取数列{xn}，limxn=?∞，

?N，?n>N：xn<?X。于是当m>n>N时，成立f(xm)?f(xn)<ε。

因而收敛。再根据相应的Heine这说明函数值数列{f(xn)}是基本数列，

定理，可知limf(x)存在而且有限。

x→?∞

42

课

后

答

案

网

w

ww

.k

n→∞x→+∞

hd

证 ?x0∈(0,+∞)，利用f(x)=f(2x)得到f(x0)=f(2nx0)，由于

limf(2nx0)=limf(x)=A，得到f(x)≡A,x∈(0,+∞)。

aw

f(x)≡A,

x∈(0,+∞)。

.c

明

om

15．设f(x)在(0,+∞)上满足函数方程f(2x)=f(x)，且limf(x)=A，证

x→+∞

习 题 3.2 连续函数

1. 按定义证明下列函数在其定义域连续： (1) y = x； (2) y = sin；

?sinx

,x≠0,

(3) y = ??x

?x=0.?1,

证 （1）函数y=x的定义域是D=[0,+∞)。设x0∈D，对任意的ε>0，

1x

取δ=ε2>0，当x?x0<δ（x∈D）时，成立

x?x0≤

x?x0<ε，

所以函数y =x在其定义域连续。

1

（2）函数y = sin的定义域是D=(?∞,0)∪(0,+∞)。设x0∈D，对任意

x

2??|x0||x0|??

的ε>0，取δ=min?,ε?>0，当x?x0<δ时，成立

2???2?

x?x02x?x01111

sin?sin≤?=<<ε， 2

xx0xx0xx0x0

所以函数y=sin在其定义域连续。

2????|x0||x0|

δ=min?,ε?>0，当x?x0<δ时，成立

???22(x0+1)?

x0sinx?xsinx0x0sinx?sinx0+sinx0x?x0sinxsinx0

?=≤ xx0xx0xx0

<

2(x0+1)x0

2

课

?sinx

,x≠0,

所以y=?在其定义域连续。 ?x

?x=0?1,

2. 确定下列函数的连续范围：

⑴y = tanx + csc x ； ⑶ y =

后

x?x0<ε，

答

可知函数在x0=0连续。设x0≠0，对任意的ε>0，取

案

1

x?sinxsinx,x≠0,

的定义域是D=(?∞,+∞)。由于lim（3）函数y=?=1，?xx→0x?x=0?1,

网

w

ww

43

.k

hd

⑵y =

(x?1)(x?3)；

x+1

⑷y = [x] ln (1+x)；

aw

.c

1

； cosx

om

（4）{x|x>?1,x?N+}。

1?k

?x?

kπ(k+1)π?

解（1）∪?,??。

k∈Z?22?

ππ?

（2）∪??+ππkk2,2??。

k∈Z?22?

（3）(?1,1]∪[3,+∞)。

?1? y =⑸?；

⑹y = sgn (sin x)。

?

（5）{(?∞,0)∪(0,+∞)}\??|k∈Z,k≠0?。

?

（6）∪(kπ,(k+1)π)。

k∈Z

是连续的。

4. 若f(x)在点x0连续，g(x)在点x0不连续，能否断言f(x)g(x)在点x0不连续?

又若f(x)与g(x)在点x0都不连续，则上面的断言是否成立?

不能断言f(x)g(x)在点x0解 若f(x)在点x0连续，g(x)在点x0不连续，

课

后

答

案

例如：f(x)=?

?1

??1

x≥0

但f2(x)或 |f(x)| 在点x0=0在点x0=0不连续，

x<0

网

w

这说明f2(x)与 |f(x)| 在点x0也连续。 反之，若f2(x)或 |f(x)| 在点x0连续，则不能断言f(x)在点x0连续。

ww

44

|f(x)|?|f(x0)|≤f(x)?f(x0)<ε，

.k

?1x≥0

在点x0=0不连

2x<0?

与

不连续：例如f(x)≡0在点x0=0连续，g(x)=?

续，但f(x)g(x)≡0在点x0=0连续。

又若f(x)与g(x)在点x0都不连续，也不能断言f(x)g(x)在点x0不连续：例如f(x)=?

?2x≥0?1x≥0

在点x0=0不连续，g(x)=?在点x0=0

?1x<0?2x<0

不连续，但f(x)g(x)≡2在点x0=0连续。

5. 若f,g在[a,b]上连续，则max {f,g}与min{f,g}在[a,b]上连续，其中

hd

f2(x)?f2(x0)=(f(x)+f(x0))(f(x)?f(x0))<(1+2f(x0))ε

aw

f(x)?f(x0)<ε，同时还有f(x)+f(x0)<1+2f(x0)，于是成立

.c

3. 若f(x)在点x0连续，证明f2(x)与 |f(x)| 在点x0也连续。反之，若f2(x)或 |f(x)| 在点x0连续，能否断言f(x)在点x0连续?

解 设f(x)在点x0连续，则?0<ε<1，?δ>0，?x(x?x0<δ)，有

om

max{f，g} = max {f(x)，g(x)}，x∈[a,b]； min {f，g} = min {f(x)，g(x)}，x∈[a,b]。

利用等证 由f,g在[a,b]上的连续性，可知f(x)?g(x)在[a,b]上连续，式

1

{f(x)+g(x)+f(x)?g(x)， 21

min{f,g}={f(x)+g(x)?f(x)?g(x)}，

2

即得到max {f,g}与min{f,g}在[a,b]上的连续性。

max{f,g}=

x→x0x→x0x→x0

x→x0

课

（1）lim??

x+1?

?

x→∞

?x?1?

后

x→x0

答

limf(x)g(x)=limeg(x)lnf(x)=eβlnα=αβ。

x→x0

2x?1x+1

=1。

2xx?1?x?1?2?

?x

2+x1???（2）lim?1lim+=????x→∞x→∞?x?1??x?1????sin

（3）lim???

x→asina??

1

x?x?a

案

?sina?

1?n?πlim+tan??。 ⑸n→∞

?4n?

证 由于lim[g(x)lnf(x)]=βlnα，利用指数函数的连续性，得到

x→a

网

w

ww

???

sinx?⑶lim???

1

x?a

.k

?????

45

x+1?

⑴lim???

x→∞

?x?1?

；

hd

????

2x?1

x+1

aw

列极限：

?x+1?

⑵lim??； x→∞

?x?1??n+x?lim?⑷n?； →∞?1n??

n

(sina≠0)；

=e2。

sinx?sina

?(x?a)sina

?

?sinx=lim??1+x→a?sina?

??

sina

?sina?sinx?sina

?n

+nx?x??lim（4）lim?=?1+???n→∞n→∞??n?1??n?1?

??

(x+1)n

n?1?n?1+1?x+1?

=ex+1。

.c

x

6. 若对任意δ>0，f 在［a +δ, b -δ］上连续，能否得出 (1) f 在(a,b)上连续? (2) f 在[a,b]上连续? 解 （1）能。（2）不能。

7. 设limf(x)=α＞0，limg(x)= β，证明：limf(x)g(x)= αβ；并求下

om

=ecota。

?

n?

11????2tan1+tan???π1??n?=lim??1+（5）limtann?+?=lim??n→∞n→∞??1??4n?n→∞?1?tan1??1tan?????

n?n????

??

1

n

1?1?tan1?tann?n?2tan??n

2ntan

?

?????

=e2。

8. 指出下列函数的不连续点，并确定其不连续的类型：

x2?1

⑴y = 3

x?3x+2x

； ⑶y = sinx

?

⑸ y = 1nex2；

x

x2?x

； ⑺y =

|x|(x2?1)

1

⑵y = [x]sin； ⑷y = [2x] - 2[x]；

1x

⑼y = ?

（6）x=0，第三类不连续点。

（7）x=0，第一类不连续点；x=1，第三类不连续点；x=?1，第二类不连续点。

（8）x=0，第三类不连续点。

（9）非整数点，第二类不连续点。

（10）非整数有理点，第三类不连续点。

9．设f(x)在(0,+∞)上连续，且满足f(x2)=f(x)，x∈(0,+∞)，证明f(x)

在(0,+∞)上为常数函数。

课

后

答

案

（4）x=k(k∈Z)，第一类不连续点。

12

（5）x=0，第三类不连续点。

网

解（1）x=1,?2，第二类不连续点。

（2）x=k(k∈Z,k≠0)，第一类不连续点；x=0，第二类不连续点。

（3）x=kπ(k∈Z,k≠0)，第二类不连续点；x=0，第三类不连续点。

w

ww

.k

?sinπx,x为有理数,

0，x为无理数;?

+3x?1

；

+2x?1

q?π

(p,q互质，p>0),?sin,x=

y = pp⑽?

?x为无理数.?0，

hd

aw

1

⑻ y =

.c

om

1

⑹y = xlnn|x|；

证 ?x∈(0,+∞)，利用f(x2)=f(x)得到f(x)=f(x2)，由limx2=1 及

n→∞

1

f(x)的连续性，得到f(x)=limf(x2)=f(1)。

n→∞

46

习 题 3.3 无穷小量与无穷大量的阶

1. 确定a与α，使下列各无穷小量或无穷大量等价于(～) axα： (1) u(x) = x5?3x4+2x3, (x→0，x→∞)；

x5+2x2 (2) u(x) = 43 (x→0，x→∞)；

3x?x

(3) u(x) = x3+ x2 (x→0+，x→+∞)； (4) u(x) =

x+x+x(x→0+，x→+∞)；

(7) u(x

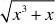
) = - x (x→0+)；

(10) u(x) = +tanx - ?sinx (x→0)。

后

解（1）u(x)～2x3(x→0)；u(x)～x5(x→∞)。

答

案

网

(9) u(x) = ln cos x - arctanx2(x→0)；

w

(8) u(x) = +xx - e2x (x→0+)；

课

（2）u(x)～?2x?1(x→0)；u(x)～x(x→∞)。 （3）u(x)～ （4）u(x)～

2

x31x8

(x→0+)；u(x)～(x→0+)；u(x)～

5

（5）u(x)～x(x→0)；u(x)～3x2(x→+∞)。

6

（6）u(x)～x?1(x→+∞)。 （7）u(x)～

1x2

12

(x→0+)。

（8）u(x)～?2x(x→0+)。

47

ww

13

3x21x2

1

.k

(x→+∞)。 (x→+∞)。

32

hd

(6) u(x) = x2+1 - x (x→+∞)；

aw

(5) u(x) = +3x - +2x (x→0，x→+∞)；

.c

om

（9）u(x)～?x2(x→0)。 （10）u(x)～x(x→0)。

2. (1) 当x→+∞时，下列变量都是无穷大量，将它们从低阶到高阶进

行排列，并说明理由。

ax (a＞1), xx, xα (α＞0)， lnkx (k＞0)， [x]!；

32

(2) 当x→0+时，下列变量都是无穷小量，将它们从高阶到低阶进

行排列，并说明理由。

xα (α＞0)，

lnkx (k＞0)，xα (α＞0)，ax (a＞1), [x]!, xx。

（2）当x→0+时，从高阶无穷小量到低阶无穷小量的排列为

?11??1?

, ax (a＞1)，xα (α＞0)， ln?k???, ?? (k＞0)。 ?1??x??x?!???x?1

证明：令y=，则当x→0+时，有y→+∞。参考（1）的排列即可得

x

课

lnkx[x]!axyk

limlim=0，=0，同时也得到limα=limαy=0 (y=lnx)。 n→∞[x]!n→∞xxx→+∞xy→+∞(e)

?

1

x

后

答

(n+1)!xα(n+1)αan+1

=0，即得到limx=0，=0，lim由lim=0与limnnn→∞n→∞n→∞x→+∞an!an

到（2）的排列。 3. 计算下列极限：

48

案

1

网

xα(n+1)α[x]!(n+1)!axan+1

0<<证明： 设n≤x<n+1，则0<x<，0<<，。nx

[x]!n!aaxnn

w

ww

.k

hd

解（1）当x→+∞时，从低阶无穷大量到高阶无穷大量的排列为

aw

1

, a?1?!??x??

?x?

.c

1

?x

1??k?1? (a＞1)，???, ln?? (k＞0)。

?x?

?

om

1

x

+x?+2x2

⑴lim； x→0ln(1+3x)

⑵lim

x→0

1?cosx

；

1?cosx

(x+x+x-x)； ⑶xlim→+∞

ax?aα

⑸lim (a＞0)； x→αx?α

(+x+x2- ?x+x2)；⑷xlim→+∞

xα?aα

⑹lim (a＞0)； x→ax?a

x ( ln (1+x) - ln x )； ⑺xlim→+∞⑼lim(x+e)；

x

x→0

1

x

⑻lim

x→a

lnx?lna

(a＞0)； x?a

12

?x?x⑽lim?； cosx???x→0?2??

.k

1?cosx

12

x?x2

1=lim=。

x→063x

hd

12

x w

（2）lim

x→0

1?cosx1?cosx

ww

aw

x→0

+x?+2x2(+x?1)?(+2x2?1)

解（1）lim=lim

x→0x→0ln(1+3x)ln(1+3x)

.c

2x

2

om

x→+∞

limn (x- 1) (x＞0)； ⑾n→∞limn2(x - nx) (x＞0)。⑿n→∞

=lim

x→0

(1?cosx)(1+cosx)

=lim

网

1

x(1+cosx)2=lim

x2x

=0。

案

（3）lim(x+x+x-x)=lim

x→+∞

x+xx+x+x+x

x→+∞

x→+∞

=

后

（4）lim(+x+x2- ?x+x2)=lim

x→+∞

答

1。 2

aα(x?α)lnaax?aαaα(ax?α?1)

（5）lim=aαlna。 =lim=lim

x→αx→αx→αx?αx?αx?α

课

+x+x+?x+x

2

=1。

（6）lim

x→a

x?a

x?aaαα?

αα

=lim

x→a

a(e?1)

=limx→ax?a

α

αln

x

a

aααln(1+

x?a

x?a

)

=lim

x→a

x?a

=αaα?1。 x?a

1ln(1+)

=1。 （7）limx ( ln (1+x) - ln x )=lim

x→+∞x→+∞1

x

49

（8）lim

x→a

lnx?lna

lim

x?ax→a

1xx+e)

ln(1+

x?a

1a=。 ax?a

x

（9）lim(x

x→0

=lim(1+x+e

x→0

1?1)x

=lim(1+

x→0

12x)x

=e2。

12

2

12

??x?xx?x2

?=lim?1?(1?cosx)??=lim1?x2x（10）lim?cos?

x→0?x→0?x→02?2?????

(1

x2

=e?1。

（11）limn (x- 1)=lim

n→∞

2

n→∞

1

lnxnn(e

1

?1)=lim(n?lnx)=lnx。

n→∞n

50

课

后

答

案

网

w

ww

.k

hd

?1???1

=lim?n2lnx????=lnx。 n→∞??nn+1??

aw

.c

1?1lnx?lnx

nnn1+?1)?(e?1)?（12）limn(x - x) =limn?(e

n→∞n→∞????

2

om

习 题 3.4 闭区间上的连续函数

1. 证明：设函数f(x)在[a,+∞)上连续，且limf(x) = A（有限数），则x→+∞

f(x)在[a,+∞)有界。

证 由limf(x) = A（有限数），可知?X>a，?x>X：f(x)?A<1，即 x→+∞

A?1<f(x)<A+1。再由f(x)在闭区间[a,X]上的连续性，可知f(x)在

[a,X]上有界，即?x∈[a,X]：f(x)<B。令M=max{B,A+1}，m=min{?B,A?1}，则?x∈[a,+∞)，成立m<f(x)<M。

证 令

答则f(x)在闭区间[a,b]连续，不妨设f(a+)<f(b?)，由闭区间上连续函~

一切值，于是f(x)在开区间(a,b)上可取到介于f(a+)和f(b-)之间的一切中间值。

3. 证明：若闭区间[a,b]上的单调有界函数f(x)能取到 f(a)和f(b)之间的一切值，则f(x)是[a,b]上的连续函数。

证 采用反证法。不妨设f(x)单调增加。若ξ∈(a,b)是f(x)的不连续点，则f(ξ?)与f(ξ+)都存在，且f(a)≤f(ξ?)<f(ξ+)≤f(b)，于是f(x)取不

与条件矛盾；若x=a是f(x)的到开区间(f(ξ?),f(ξ+))中异于f(ξ)的值，

51课后数的中间值定理，可知f(x)在闭区间[a,b]上可取到[f(a+),f(b?)]上的案网?f(x)x∈(a,b)~?f(x)=?f(a+)x=a， ?f(b?)x=b?~ www.khd它可取到介于f(a+)和f(b-)之间的一切中间值。 aw2. 证明：若函数f(x)在开区间(a,b)上连续，且f(a+)和f(b-)存在，则.com

不连续点，则f(a+)存在，且f(a)<f(a+)≤f(b)，于是f(x)取不到开区间(f(a),f(a+))中的值，也与条件矛盾；同样可以证明x=b也不可能是f(x)的不连续点。

4. 应用Bolzano-Weierstrass定理证明闭区间上连续函数的有界性定理。

证 采用反证法。设f(x)在闭区间[a,b]上连续，但无界，则存在点列{xn}，xn∈[a,b]，满足f(xn)>n，即limf(xn)=∞。由Bolzano-Weierstrassn→∞

k→∞

k→∞n→∞

如果f(a2+b2a+b2a+b2=0，则定理得证。如果f(2)<0，则令a3=2，222

a2+b2a+b2>0，则令a3=a2，b3=2。 22b3=b2；如果f(

"", 课后b2=b1；如果f(a1+b1a+b)>0，则令a2=a1，b2=11。 22答案如果f(a1+b1a+ba+b)=0，则定理得证。如果f(11)<0，则令a2=11，222网 wf(a)<0，f(b)>0。 ww证 设f(x)在闭区间[a,b]上连续，且f(a)f(b)<0，不妨设a=a1，b=b1，.khd

ak+bk)=0，2

ak+bk=0，则得到一个闭25. 应用闭区间套定理证明零点存在定理。 这样的过程可以一直进行下去。如果存在某个k，使得f(则定理得证；如果不存在某个k，使得f(

区间套{[an,bn]}，满足f(an)<0，f(bn)>0。由闭区间套定理，可知存 52aw所以有limf(xnk)=f(ξ)，与limf(xn)=∞产生矛盾。 .com定理，存在子列{xnk}，limxnk=ξ，且ξ∈[a,b]。因为f(x)在点ξ连续，

在唯一属于所有闭区间[an,bn]的点ξ，且liman=limbn=ξ。再由f(x)在

n→∞

n→∞

点ξ的连续性，可知f(ξ)=limf(an)≤0与f(ξ)=limf(bn)≥0，从而得到

n→∞

n→∞

f(ξ)=0，定理得证。

6. 证明方程x=asinx+b（a,b>0）至少有一个正根。

证 令f(x)=x?asinx?b，则f(x)在[0,+∞)上连续。取A>a+b，则

由零点存在定理，f(x)在(0,A)上至少有一个根。 f(0)<0，f(A)>0，

7．证明方程x3+px+q=0（p>0）有且仅有一个实根。

证 令f(x)=x3+px+q，则f(x)在(?∞,+∞)上是严格单调增加的。由

x→?∞

x→+∞

8．证明：

（2）sinx2在(?∞,+∞)上不一致连续，但在[0,A]上一致连续；

(5) cosx在[0,+∞)上一致连续。

'证（1）在(0,1)上，令xn=

课

后

（4）ln x在[1,+∞)上一致连续；

答

（3）x在[0,+∞)上一致连续；

案

网

w

1

（1）sin在（0,1）上不一致连续，但在(a,1)(a＞0)上一致连续；

x

1"

，xn=nπ

ww

sin

111

，所以sin在（0,1）上不一致连续。 ?sin=1'"xxnxn

在(a,1) (a＞0)上，?ε>0，取δ=a2ε>0，?x1,x2∈(a,1)x1?x2<δ， 成立

sin

x1?x21111?sin≤?≤<ε， 2x1x2x1x2a

53

.k

1nπ+

hd

2

'"

?xn→0，但 ，xn

实根。

aw

limf(x)=?∞，limf(x)=+∞，易知f(x)在(?∞,+∞)上有且仅有一个

.c

om

所以sin在(a,1) (a＞0)上一致连续。

'=nπ+（2）在?∞,+∞)上，令xn1x2

2"'"=nπ，则xn?xn→0，但 ，xn'sinxn()2"?sinxn()

ε=1， 所以sinx2在(?∞,+∞)上不一致连续。 在[0,A]上，?ε>0，取δ=

立 2A>0，?x1,x2∈[0,A]，x1?x2<δ，成

?ε>0，取δ=ε2>0，?x1,x2∈[0,+∞)，x1?x2<δ，成立 （3）

网?ε>0，取δ=ε>0，?x1,x2∈[1,+∞)，0≤x1?x2<δ，成立 （4）

?x1?x2lnx1?lnx2=ln?1+?x2????≤x1?x2<ε， ?

?ε>0，取δ=ε2>0，?x1,x2∈[0,+∞)，x1?x2<δ，成立 （5）

cosx1?cosx2≤x1?x2≤x1?x2<ε，

所以cosx在[0,+∞)上一致连续。

9．证明：对椭圆内的任意一点P，存在椭圆过P的一条弦，使得P是该弦的中点。

证 过P点作弦，设弦与x轴的夹角为θ，P点将弦分成长度为l1(θ)和l2(θ)的两线段，则f(θ)=l1(θ)?l2(θ)在[0,π]连续，满足f(0)=?f(π)，于 54课后所以ln x在[1,+∞)上一致连续。 答案 www所以x在[0,+∞)上一致连续。 .kx1?x2≤x1?x2<ε， hdaw.c所以sinx2在[0,A]上一致连续。 om222sinx12?sinx2≤x1?x2≤2Ax1?x2<ε，

是必有θ0∈[0,π]，满足f(θ0)=0，也就是l1(θ0)=l2(θ0)。

10．设函数f(x)在[0,2]上连续，且f(0) = f(2)，证明：存在x,y∈[0,2]，y?x=1，使得f(x)=f(y)。

证 令F(x)=f(x+1)?f(x)，则F(x)在[0,1]上连续，F(1)=?F(0)，于是必有x0∈[0,1]，满足F(x0)=0。令y0=x0+1，则x0,y0∈[0,2]，y0?x0=1，使得f(x0)=f(y0)。

11．若函数f(x)在有限开区间(a,b)上一致连续，则f(x)在(a,b)上有界。 证 由f(x)在(a,b)上一致连续，可知f(a+)，f(b?)存在且有限。令

?f(x)x∈(a,b)~?f(x)=?f(a+)x=a，

?f(b?)x=b?

~~则f(x)在闭区间[a,b]连续，所以f(x)在[a,b]有界，因此f(x)在(a,b)上

12．证明：

证（1）设函数f(x)，g(x)在区间I上一致连续，则?ε>0，?δ>0， ?x',x"∈I，x'?x"<δ，成立f(x')?f(x")<课后 （2）某区间上两个一致连续函数之积不一定一致连续。 答 （1）某区间上两个一致连续函数之和必定一致连续； 案网 w有界。 wwε

2.khd，g(x')?g(x")<，于是 2awε

f(x')+g(x')]?[f(x")+g(x")]<ε，

所以f(x)+g(x)在区间I上一致连续。

（2）设f(x)=g(x)=x，区间I=[0,+∞)，则f(x)，g(x)在区间I上一致连续，但f(x)g(x)=x2在区间I上不一致连续。

证明f(x)在[a,b]上13. 设函数f(x)在[a,b]上连续，且f(x)≠0,x∈[a,b]，

55.com

恒正或恒负。

， 证 设f(x)在[a,b]上不保持定号，则存在x',x"∈[a,b]（不妨设x'<x"）

使f(x')与f(x")不同号，由闭区间上连续函数的中间值定理，必定存 在ξ∈[x',x"]，使得f(ξ)=0，这就产生矛盾，所以f(x)在[a,b]上必定恒 正或恒负。

14．设函数f(x)在[a,b]上连续，a≤x1<x2<"<xn≤b，证明在[a,b]中必有ξ，使得

f(ξ)=

f(ξ)=

由于f(x) 证 由limf(x)=A，?ε>0,?X>a,?x',x">X:f(x')?f(x")<ε。x→+∞

在[a,X+1]连续，所以一致连续，也就是

?0<δ<1,?x',x"∈[a,X+1](x'?x"<δ):f(x')?f(x")<ε。于是 ?x',x"∈[a,+∞)(x'?x"<δ):f(x')?f(x")<ε。

56课后[a,+∞)上一致连续。 答15．若函数f(x)在[a,+∞)上连续，且limf(x) = A(有限数)，则f(x)在x→+∞案1[f(x1)+f(x2)+"+f(xn)]。 n网 w所以在[a,b]中必有ξ，使得 wwx∈[a,b]min{f(x)}≤1{f(x)}， [f(x1)+f(x2)+"+f(xn)]≤xmax∈[a,b]n.khd取到最大值和最小值之间任何一个值。由于 aw证 根据闭区间上连续函数的中间值定理，闭区间上连续函数一定能.c1[f(x1)+f(x2)+"+f(xn)]。 nom