数值分析MATLAB实验程序

时间：2024.3.31

数值分析

上机实验报告

院系:XXX

学号:XXX

姓名:XXXX

一．Gass-Jordan消去法... 1

二．雅克比迭代法... 2

三．拉格朗日多项式插值... 4

四．埃尔米特插值法... 5

五．复化梯形公式... 7

六．龙贝格求积公式... 8

七．欧拉法... 9

八．隐式欧拉法... 11

一．Gass-Jordan消去法

Gass-Jordan消去法求解线性方程组的基本思想是将系数矩阵化为对角矩阵，这样可以直接得到方程组的解x₁, x₂…x_n，因此也称为无回代消去法。

例：用列主元Gass-Jordan消去法求解方程组：

2x₁+1x₂+x₃=5

5x₁-1x₂+1x₃=8

1x₁-3x₂-4x₃=-4

编写Gau_Jor 函数来实现求解：

function [x,flag]=Gau_Jor(A,b)

% 求线性方程组的列主元Gauss－Jordan消去法

% A为方程组的系数矩阵；

% b为方程组的右端项；

% x为方程组的解；

% flag为指标向量，flag＝'failure'表示计算失败，flag='OK'表示计算成功。

[n,m]=size(A);nb=length(b);

% 当方程组行与列的维数不相等时，停止计算，并输出出错信息

if n~=m

error('The rows and columns of matrix A must be equal!');

return;

end

% 当方程组与右端项的维数不匹配时，停止计算，并输出出错信息

if m~=nb

error('The columns of A must be equal the length of b!');

return;

end

% 开始计算，先赋初值

flag='OK';x=zeros(n,1);

for k =1:n

% 选主元

max1=0;

for i=k:n

if abs(A(i,k))>max1

max1=abs(A(i,k));r=i;

end

if max1<1e-10

falg='failure';return;

end

% 交换两行

if r>k

for j =k:n

z=A(k,j);A(k,j)=A(r,j);A(r,j)=z;

end

z=b(k);b(k)=b(r);b(r)=z;

end

%消元计算

b(k)=b(k)/A(k,k);

for j=k+1:n

A(k,j)=A(k,j)/A(k,k);

end

for i=1:n

if i~=k

for j =k+1:n

A(i,j)=A(i,j)-A(i,k)*A(k,j);

end

b(i)=b(i)-A(i,k)*b(k);

end

% 输出x

for i=1:n

x(i)=b(i);

end

在命令窗口输入：

clear

A=[2 1 2;5 -1 1;1 -3 -4];

b=[5 8 -4];

x=Gau_Jor(A,b )

运行程序，输出如下：

x =

1.0000

-1.0000

2.0000

二．雅克比迭代法

求解线性方程组Ax = b时，一般当A为低阶稠密矩阵时，用主元消去法求解是常用方法。但是，对于由工程技术中产生的大型稀疏矩阵方程组(A)阶数很高，但零元素较多，例如求某些偏微分方程数值解所产生的线性方程组)，利用迭代法求解此方程组就是合适的，在计算机内存和运算两方面，迭代法通常都可利用A中有大量零元素的特点。雅克比迭代法就是众多迭代法中比较早且较简单的一种。

例：用雅克比迭代法求解方程组：

10 x₁- x₂=9

- x₁+10 x₂- 2 x₃=7

-2 x₁+10 x₂=6

编写jacobi函数来实现求解：

function x=jacobi(A,b,P,delta,n)

%A为n维非奇异阵；b为n维值向量

% P为初值；delta为误差界；n为给定的迭代最高次数

N=length(b);

for k=1:n

for j=1:N

x(j)=(b(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j);

end

err=abs(norm(x'-P));

P=x';

if(err<delta)

break;

end

x=x';

k,err

在命令窗口输入：

clear

A=[10 -1 0;-1 10 -2;0 -2 10];

b=[9 7 6]';

P=[0 0 0]'; %给出初值

x=jacobi(A,b,P,1e-4,20)

运行程序，输出如下：

P =

0.9958

0.9579

0.7916

k =

err =

3.2740e-005

x =

0.9958

0.9579

0.7916

三．拉格朗日多项式插值

例：已知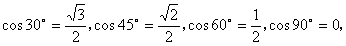使用Lagrange多项式插值法计算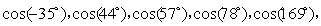并给出插值多项式。

编写Lagrange函数来实现求解：

function s=Lagrange(x,y,x0)

%Lagrange.m函数为求已知数据点的拉格朗日插值多项式

%x为数据点的x坐标向量

%y为数据点的y坐标向量

%x0为插值的x坐标

%s为求得的拉格朗日插值多项式或在x0处的插值

syms p;

n=length(x); %读取x向量维数

s=0;

for(k=1:n)

la=y(k);

for(j=1:k-1)

la=la*(p-x(j))/(x(k)-x(j));

end;

for(j=k+1:n)

la=la*(p-x(j))/(x(k)-x(j));

end;

s=s+la;

simplify(s);

end

%对输入参数个数做判断，如果只有两个参数,直接给出插值多项式

%如果三个参数则给出插值点的插值结果 ,第三个参数可以为向量

if(nargin==2)

s=subs(s,'p','x');

s=collect(s); %多项式展开

s=vpa(s,4); %把系数取到6位精度表达

else

m=length(x0); %读取x0长度

%分别对x0的每一个分量插值

for i=1:m

temp(i)=subs(s,'p',x0(i));

end

%得到的是系列插值点的插值结果

s=temp;

end

在命令窗口输入：

clear

x=[pi/4, pi/6,pi/3,pi/2];

y=[cos(pi/4), cos(pi/6), cos(pi/3), cos(pi/2)];

x0=[-35*pi/180, 44*pi/180, 57*pi/180,78*pi/180, 169*pi/180];

disp('角度')

du=[-35 44 57 78 169]

disp('插值结果')

yt=Lagrange(x,y,x0)

disp('cos 函数值')

yreal=[cos(-35*pi/180)

cos(44*pi/180)

cos(57*pi/180)

cos(78*pi/180)

cos(169*pi/180)]'

disp('插值与函数值误差')

dy=yt-yreal

yt= Lagrange(x,y)

运行程序，输出如下：

角度

du =

-35 44 57 78 169

插值结果

yt =

0.6394 0.7194 0.5446 0.2086 -1.0890

cos 函数值

yreal =

0.8192 0.7193 0.5446 0.2079 -0.9816

插值与函数值误差

dy =

-0.1798 0.0000 -0.0001 0.0006 -0.1074

yt =

0.1365*x^3 - 0.6731*x^2 + 0.09636*x + 0.9805

四．埃尔米特插值法

埃尔米特插值要求插值多项式在插值点处的取值与函数值相等，而且还要求导数相同。

例：根据下表所列数据点求出其Hermite插值多项式，并计算当x=2.0时的y值。

编写Hermite函数来实现求解：

function f = Hermite(x,y,y_1,x0)

%Hermite.m插值求已知数据点的埃尔米特插值多项式

%x为数据点的x坐标向量

%y为数据点的y坐标向量

%x0为插值的x坐标

% y_1为函数的导数向量

%f为求得的埃尔米特插值多项式或在x0处的插值

syms t;

f = 0.0;

if(length(x) == length(y))

if(length(y) == length(y_1))

n = length(x);

else

disp('y和y的导数的维数不相等！');

return;

end

else

disp('x和y的维数不相等！');

return;

end

for i=1:n

h = 1.0;

a = 0.0;

for j=1:n

if( j ~= i)

h = h*(t-x(j))^2/((x(i)-x(j))^2);

a = a + 1/(x(i)-x(j));

end

f = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));

if(i==n)

if(nargin == 4)

f = subs(f,'t',x0);

else

f = vpa(f,6);

end

在命令窗口输入：

clear

x=[ 1 1.2 1.4 1.6 1.8];

y=[1 1.0954 1.1832 1.2649 1.3416];

y_1=[0.5000 0.4564 0.4226 0.3953 0.3727];

disp('显示Hermite插值多项式：')

f = Hermite (x,y,y_1)

disp('显示在 x=2处的Hermite插值：')

f = Hermite (x,y, y_1,2)

运行程序，输出如下：

显示Hermite插值多项式：

f =

24414.1*(t - 1.8)^2*(t - 1.6)^2*(t - 1.2)^2*(t - 1.0)^2*(0.4226*t + 0.59156) - 678.168*(27.5773*t - 50.9807)*(t - 1.6)^2*(t - 1.4)^2*(t - 1.2)^2*(t - 1.0)^2 - 10850.7*(10.1455*t - 17.4978)*(t - 1.8)^2*(t - 1.4)^2*(t - 1.2)^2*(t - 1.0)^2 + 678.168*(21.3333*t - 20.3333)*(t - 1.8)^2*(t - 1.6)^2*(t - 1.4)^2*(t - 1.2)^2 + 10850.7*(9.58473*t - 10.4063)*(t - 1.8)^2*(t - 1.6)^2*(t - 1.4)^2*(t - 1.0)^2

显示在 x=2处的Hermite插值：

f =

1.4112

五．复化梯形公式

例：用复化梯形积分公式求函数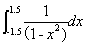的积分，取区间个数n为10。

编写Comtrap函数来实现求解：

function s=Comtrap(f,a,b,n)

% Comtrap.m函数为复合梯形公式积分

% f为被积函数；a与b为积分的上下限；

% n为子区间的个数；s为梯形总面积，即所求积分数值

h=(b-a)/(2*n);

s1=0;

s2=0;

for k=1:n

x=a+h*(2*k-1);

s1=s1+feval('f',x);

end

for k=1:(n-1);

x=a+h*2*k;

s2=s2+feval('f',x);

end

s=h*(feval('f',a)+feval('f',b)+4*s1+2*s2)/3;

再建立被积函数的M文件：

function y=f(x);

y=1/(1-x^2);

在命令窗口输入：

clear

a0=-1.5;

b0=1.5;

n=10;

s=Comtrap('f',a0,b0,n)

运行程序，输出如下：

s =

3.7267

六．龙贝格求积公式

例：用龙贝格求积公式求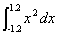的积分。

编写remberg函数来实现求解：

function [I,step]=romberg(f,a,b,eps)

% romberg.m为用龙贝格求积分

% f为被积函数；

% a,b为积分区间的上下限

% eps为积分结果精度

% I为积分结果；step为积分的子区间数

if(nargin==3)

eps=1.0e-4;

end;

M=1;

tol=10;

k=0;

T=zeros(1,1);

h=b-a;

T(1,1)=(h/2)*(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsym(sym(f)),b));

while tol>eps

k=k+1;

h=h/2;

Q=0;

for i=1:M

x=a+h*(2*i-1);

Q=Q+subs(sym(f),findsym(sym(f)),x);

end

T(k+1,1)=T(k,1)/2+h*Q;

M=2*M;

for j=1:k

T(k+1,j+1)=T(k+1,j)+(T(k+1,j)-T(k,j))/(4^j-1);

end

tol=abs(T(k+1,j+1)-T(k,j));

end

I=T(k+1,k+1);

step=k;

在命令窗口输入：

clear

a=-1.2;b=1.2;eps=1e-6;

[I,step]=romberg('x^2',a,b,eps)

运行程序，输出如下：

I =

1.1520

step =

七．欧拉法

例：用欧拉法求下面一阶常微分方程的数值解。

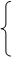
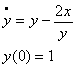
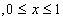
编写Euler函数来实现求解：

function x = Euler(f,x0,y0,xn,N)

% Euler.m函数为用欧拉法求解微分方程

% f为一阶常微分方程的一般表达式的右端函数；

% x0,y0为初始条件

% xn为取值范围的一个端点；

% N为区间的个数；

% x为求解微分方程组的值

x=zeros(1,N+1); %x为Xn构成的向量

y=zeros(1,N+1); %y为Yn构成的向量

x(1)=x0;

y(1)=y0;

h=(xn-x0)/N;

for n=1:N

x(n+1)=x(n)+h;

y(n+1)=y(n)+h*feval(f,x(n),y(n));

end

T=[x',y']

编写常微分方程的M文件：

function z=fun1(x,y)

z=y-2*x/y;

在命令窗口输入：

clear

x0=0;y0=1;xn=1;n=10;

x=Euler('fun1',x0,y0,xn,n);

运行程序，输出如下：

T =

0 1.000000000000000

0.100000000000000 1.100000000000000

0.200000000000000 1.191818181818182

0.300000000000000 1.277437833714722

0.400000000000000 1.358212599560289

0.500000000000000 1.435132918657796

0.600000000000000 1.508966253566332

0.700000000000000 1.580338237655217

0.800000000000000 1.649783431047711

0.900000000000000 1.717779347860087

1.000000000000000 1.784770832497982

八．隐式欧拉法

例：用隐式欧拉法求下面一阶常微分方程的数值解。

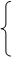
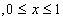
编写diEuler函数来实现求解：

function x=diEuler(f,x0,y0,xn,N)

% diEuler.m为隐式欧拉法求微分方程的数值解

% f为一阶常微分方程的一般表达式的右端函数；

% x0,y0为初始条件

% xn为取值范围的一个端点；

% n为区间的个数；

% x为求解微分方程组的值

x=zeros(1,N+1); %x为Xn构成的向量

y=zeros(1,N+1); %y为Yn构成的向量

x(1)=x0;

y(1)=y0;

h=(xn-x0)/N;

for n=1:N

%用迭代法求y(n+1)

x(n+1)=x(n)+h;

z0=y(n)+h*feval(f,x(n),y(n));

for k=1:3

z1=y(n)+h*feval(f,x(n+1),z0);

if abs(z1-z0)<1e-3;

break;

end

z0=z1;

end

y(n+1)=z1;

end

T=[x',y' ]

编写常微分方程的M文件：

function z=fun2(x,y)

z=y-3*x;

在命令窗口输入：

clear

x0=0;y0=0.1;xn=1;n=10;

x=diEuler('fun2',x0,y0,xn,n);

运行程序，输出如下：

T =

0 0.1000

0.1000 0.0778

0.2000 0.0198

0.3000 -0.0779

0.4000 -0.2199

0.5000 -0.4109

0.6000 -0.6565

0.7000 -0.9628

0.8000 -1.3363

0.9000 -1.7847

1.0000 -2.3163

更多相关推荐：

数值分析实验报告(一)(完整): 数值分析实验报告123456
数值分析实验报告(包含源程序): 课程实验报告课程实验报告课程实验报告课程实验报告
哈工大-数值分析上机实验报告: 实验报告一题目非线性方程求解摘要非线性方程的解析解通常很难给出因此线性方程的数值解法就尤为重要本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法前言目的和意义掌握二分法与Newton法的基...
数值分析实验报告: 数值分析实验报告册课程实验报告专业年级课程名称数值分析指导教师学生姓名学号实验日期实验地点实验成绩教务处制20xx年6月20日实验名称Lagrange插值实验一实验目的数值分析实验报告册掌握Lagrange插值...
数值分析matlab完整版实验报告: 数值分析报告运用Matlab求解非线性方程的根学院专业班级姓名学号数值分析报告1目的掌握非线性方程求根的方法并选取实例运用MATLAB软件进行算法的实现分别用牛顿法弦截法和抛物线法求非线性方程的根2报告选题报告...
数值分析实验报告: 实验21多项式插值的振荡现象实验目的在一个固定的区间上用插值逼近一个函数显然Lagrange插值中使用的节点越多插值多项式的次数就越高我们自然关心插值多项式的次数增加时Lnx是否也更加靠近被逼近的函数Runge...
数值分析实验报告三: 数学与信息工程学院实课程名称实验室实验台号班级姓名实验日期验报告计算方法740420xx年5月21日

数值分析上机实验报告七: 西安工程大学数值计算方法实验报告实验报告七题目线性方程组的直接解法摘要在数值计算中关于线性方程组的解法有两类直接法和迭代法本实验研究线性方程组的直接解法前言目的和意义掌握线性方程组的直接解法如高斯消去法LU解法...
数值实验报告: 重庆交通大学学生实验报告实验课程名称开课实验室数学实验室学院理学院年级09专业班学生姓名学号开课时间至学期实验五解线性方程组的直接方法实验51主元的选取与算法的稳定性问题提出Gauss消去法是我们在线性代数中已...
电子科技MATLAB与数值分析第一次实验教学及内容 - 副本: 第一次实验教学的具体安排第一次实验教学1MATLAB软件操作及程序设计实验内容具体实验要求及相关内容见实验一实验时间第7周的周一到周三晚上19002130实验方式混合班学生按照自己的时间自由安排但必须带本人学生...
数值分析上机实验报告: 实验报告一题目非线性方程求解摘要非线性方程的解析解通常很难给出因此线性方程的数值解法就尤为重要本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法前言目的和意义掌握二分法与Newton法的基...
数值分析实验报告: 第一次作业题目作业1试使用subplot命令生成11上的第二个至第五个Chebyshev多项式并按照22方式多窗口显示选做题12应用秦九韶算法计算多项式10110nn0nnpxaxaxaxaaL在xx处的函数值...

热门关注

数值分析实验报告 (用样条插值法插值的方法生成字体T的轮廓,高斯消去法的实现)

数值分析实验报告--Runge现象的产生和克服

数值分析实验报告第二章

数值分析实验报告