
《数值计算方法实验报告》
专业: 应用数学
年级: 大学本科二年级
班级: 应数11102班
学号: 1104991115
姓名: 徐沈和
成绩:
20##年6月9日
一,实验名称:
复化求积法
二,实验题目
测得飞机在高空h时的上升速度v(h)的数据如下表一所示:
表一:v(h)的数据

飞机从地面上升到H km高度所需要的时间可用公式:
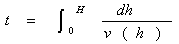
分别用复化梯形公式和复化Simspon公式计算飞机上升到8 km高空所需要的时间。
三,试验目的:
1. 本次试验是利用编程,来研究定积分的数值计算方法;
2. 实现复化梯形公式和复化Simspon公式的算法;
3.加深对复化梯形公式和复化Simspon公式的算法的理解
。
4,实现灵活应数复化梯形公式和复化Simspon公式求解现实中的问题。
四,基础理论:
1.复化梯形公式
在每个小区间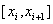 (i=0,1,...,n-1)上使用梯形公式,即:
(i=0,1,...,n-1)上使用梯形公式,即:
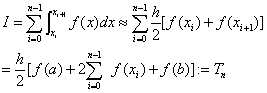 ……………(1)
……………(1)
式(1)即称为 复化梯形公式。
2.复化Simspon公式
在每个小区间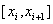 二等分,记其二等分点为
二等分,记其二等分点为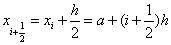 ,最后在每个小区间
,最后在每个小区间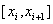 (i=0,1,...,n-1)上使用Simspon公式,即:
(i=0,1,...,n-1)上使用Simspon公式,即:
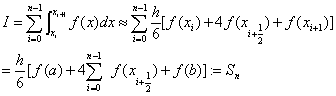 ………(2)
………(2)
式(2)即称为 复化Simspon公式。
五,实验环境:
本次试验使用的是:windows 7操作系统,MATLAB 软件
六,实验过程
先分别用复化梯形公式和复化Simpson公式笔算
复化梯形公式:T(8)=8/(2*4)*(1/50+2*1/46+2*1/40+2*1/32.2+1/22.5)=0.2200345(s)
复化Simpson:T(8)=8/(6*2)*(1/50+4*1/46+2*1/40+4*1/32.2+1/22.5)=0.21708305(s)
然后用matlaB根据复化梯形公式与复化Simpson公式的推导思想,编出程序并求解.
七.结果分析:
运行结果截图
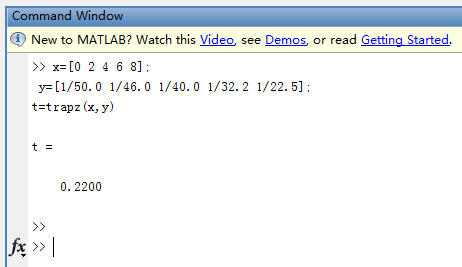
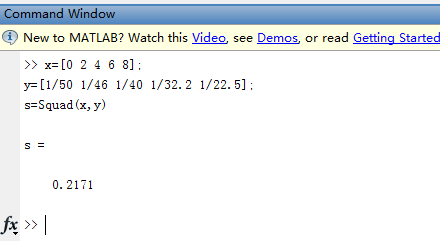
即:通过编写的复化梯形公式(Tformula)和复化Simspon公式(Sformula)的代码,计算出估计值,分别为0.2200和0.2171,由这两种方法求得的结果比较可知,程序运行正确.
八,附录程序清单
1.复化梯形公式程序代码:
function T=trapz(x,y)
n=length(x);m=length(y);
if n~=m
error('数列长度不一致,输入有错误 ');
return
end
T=0;
N=n-1;
h=(x(n)-x(1))/N;
for k=1:N
T=T+y(k)+y(k+1);
end
T=(h/2)*T;
2.复化Simspon公式程序代码:
function S=Squad(x,y)
if length(x)~=length(y)
error(' 数列长度不一致,输入有误');
return
end
if rem(length(x)-1,2)~=0
S=Trapz(x,y);
return;
end
n=length(x);m=length(y);
S=0;
N=(n-1)/2;
h=(x(n)-x(1))/N;
for k=1:N
S=S+y(2*k-1)+4*y(2*k)+y(2*k+1);
end
S=(h/6)*S;
3.调用复化梯形公式程序代码:
x=[0 2 4 6 8];
y=[1/50.0 1/46.0 1/40.0 1/32.2 1/22.5];
t=Trapz(x,y)
4.调用复化Simspon公式程序代码:
x=[0,2,4,6,8];
y=[1/50.0 1/46.0 1/40.0 1/32.2 1/22.5];
t=Squad(x,y)
第二篇:数值计算方法上机实验报告
数值计算方法上机实验报告
实验目的:复习和巩固数值计算方法的基本数学模型,全面掌握运用计算机进行数值计算的具体过程及相关问题。利用计算机语言独立编写、调试数值计算方法程序,培养学生利用计算机和所学理论知识分析解决实际问题的能力。
上机练习任务:利用计算机基本C语言编写并调试一系列数值方法计算通用程序,并能正确计算给定题目,掌握调试技能。
掌握文件使用编程技能,如文件的各类操作,数据格式设计、通用程序运行过程中文件输入输出运行方式设计等。
一、 各算法的算法原理及计算机程序框图
1. 列主元高斯消去法
l 算法原理:
高斯消去法是利用现行方程组初等变换中的一种变换,即用一个不为零的数乘一个方程后加只另一个方程,使方程组变成同解的上三角方程组,然后再自下而上对上三角方程组求解。
列选住院是当高斯消元到第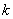 步时,从
步时,从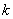 列的
列的 以下(包括
以下(包括 )的各元素中选出绝对值最大的,然后通过行交换将其交换到
)的各元素中选出绝对值最大的,然后通过行交换将其交换到 的位置上。交换系数矩阵中的两行(包括常数项),只相当于两个方程的位置交换了,因此,列选主元不影响求解的结果。
的位置上。交换系数矩阵中的两行(包括常数项),只相当于两个方程的位置交换了,因此,列选主元不影响求解的结果。


l 计算机程序框图如上
l 源程序:
#define N 200
#include "stdio.h"
#include "math.h"
FILE *fp1,*fp2;
void LZ()
{
int n,i,j,k=0,l;
double d,t,t1;
static double x[N],a[N][N];
fp1=fopen("a1.txt","r");
fp2=fopen("b1.txt","w");
fscanf(fp1,"%d",&n);
for(i=0;i<n;++i)
for(j=0;j<=n;++j)
{
fscanf(fp1,"%lf",&a[i][j]);
}
do
{
d=a[k][k];
l=k;
i=k+1;
do
{
if(fabs(a[i][k])>fabs(d)) /*选主元*/
{
d=a[i][k];
l=i;
}
i++;
}while(i<n);
if(d==0)
{printf("\n输入矩阵有误!\n");}
else
{ /*换行*/
if(l!=k)
{
for(j=k;j<=n;j++)
{
t=a[l][j];
a[l][j]=a[k][j];
a[k][j]=t;
}
}
}
for(j=k+1;j<=n;j++) /*正消*/
a[k][j]/=a[k][k];
for(i=k+1;i<n;i++)
for(j=k+1;j<=n;j++)
a[i][j]-=a[i][k]*a[k][j];
k++;
}while(k<n);
if(k!=0)
{
for(i=n-1;i>=0;i--) /*回代*/
{
t1=0;
for(j=i+1;j<n;j++)
t1+=a[i][j]*x[j];
x[i]=a[i][n]-t1;
}
}
for(i=0;i<n;i++)
fprintf(fp2,"\n方程组的根为x[%d]=%lf",i+1,x[i]);
fclose(fp1);
fclose(fp2);
}
main()
{
LZ();
}
l 具体算例及求解结果:
用列选主元法求解下列线性方程组
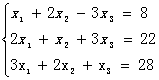
输入3 输出结果:方程组的根为x[1]=6.000000
1 2 -3 8 方程组的根为x[2]=4.000000
2 1 3 22 方程组的根为x[3]=2.000000
3 2 1 28
l 输入变量、输出变量说明:
输入变量: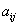 系数矩阵元素,
系数矩阵元素,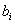 常向量元素
常向量元素
输出变量: 解向量元素
解向量元素
2. 杜里特尔分解法解线性方程
l 算法原理:
求解线性方程组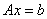 时,当对
时,当对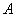 进行杜里特尔分解,则等价于求解
进行杜里特尔分解,则等价于求解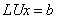 ,这时可归结为利用递推计算相继求解两个三角形(系数矩阵为三角矩阵)方程组,用顺代,由
,这时可归结为利用递推计算相继求解两个三角形(系数矩阵为三角矩阵)方程组,用顺代,由

求出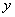 ,再利用回带,由
,再利用回带,由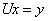 求出
求出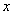 。
。
计算机程序框图:
源程序:#include "stdio.h"
#include "math.h"
FILE *fp1,*fp2;
void main()
{
int i,j,k,N;
double s,A[200][200],B[200],x[200],y[200];
static double L[200][200],U[200][200];
fp1=fopen("a2.txt","r");
fp2=fopen("b2.txt","w");
fscanf(fp1,"%d",&N);
for(i=0;i<N;i++)
{for(j=0;j<N;j++)
fscanf(fp1,"%lf",&A[i][j]);
}
for(i=0;i<N;i++)
fscanf(fp1,"%lf",&B[i]);
for(i=0;i<N;i++) /*LU分解*/
{
for(j=i;j<N;j++)
{
s=0.0;
for(k=0;k<i;k++)
s+=L[i][k]*U[k][j];
U[i][j]=A[i][j]-s;
}
for(j=i+1;j<N;j++)
{
s=0.0;
for(k=0;k<i;k++)
s+=U[k][i]*L[j][k];
L[j][i]=(A[j][i]-s)/U[i][i];
}
}
for(i=0;i<N;i++)
for(j=0;j<N;j++)
L[i][i]=1;
fprintf(fp2,"\nU矩阵为:");
for(i=0;i<N;i++)
{fprintf(fp2,"\n");
for(j=0;j<N;j++)
fprintf(fp2,"%10.3f",U[i][j]);
}
fprintf(fp2,"\nL矩阵为:");
for(i=0;i<N;i++)
{fprintf(fp2,"\n");
for(j=0;j<N;j++)
fprintf(fp2,"%10.3f",L[i][j]);
}
for(i=0;i<N;i++)
{s=0.0;
for(k=0;k<i;k++)
s+=L[i][k]*y[k];
y[i]=B[i]-s;
}
for(i=N-1;i>=0;i--)
{s=0.0;
for(k=i+1;k<N;k++)
s+=U[i][k]*x[k];
x[i]=(y[i]-s)/U[i][i];
}
fprintf(fp2,"\n方程组解为:");
for(i=0;i<N;i++)
fprintf(fp2,"\nx%d=%10.3f",i+1,x[i]);
fclose(fp1);
fclose(fp2);
}
l 具体算例及求解结果:
用杜里特尔分解法求解方程组
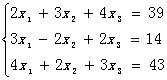
输入数据 输出结果:U矩阵为:
2.000 3.000 4.000
0.000 -6.500 -4.000
0.000 0.000 -2.538
3 L矩阵为:
2 3 4 1.000 0.000 0.000
3 -2 2 1.500 1.000 0.000
4 2 3 2.000 0.615 1.000
39 14 43 方程组解为:
x1= 6.000
x2= 5.000
x3= 3.000
l 输入变量、输出变量说明:
输入变量: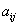 系数矩阵元素,
系数矩阵元素,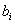 常向量元素
常向量元素
输出变量: 解向量元素
解向量元素
3. 拉格朗日插值法
l 算法原理:
首先构造基函数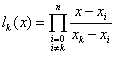 ,可以证明基函数满足下列条件:
,可以证明基函数满足下列条件:
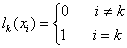 ,
,
对于给定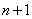 个节点,
个节点,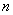 次拉格朗日插值多项式由下式给出:
次拉格朗日插值多项式由下式给出:
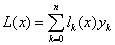
其中
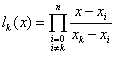
由于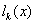 是一个关于
是一个关于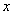 的
的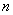 次多项式,所以
次多项式,所以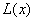 为关于
为关于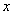 的不高于
的不高于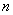 次的代数多项式。当
次的代数多项式。当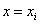 时,
时,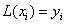 ,满足插值条件。
,满足插值条件。
l 计算机程序框图:
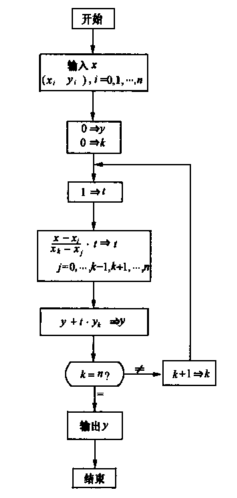
源程序:#include"stdio.h"
#include"math.h"
int n,m,i,j;
float x2,x3,z1=0.0,z=0.0,t,x[50],y[50],c[50],A[50];
main()
{FILE *fp1,*fp2;
fp1=fopen("a3.txt","r");
fp2=fopen("b3.txt","w");
fscanf(fp1,"%d",&n);
for(i=0;i<n;i++)
fscanf(fp1,"%f,%f",&x[i],&y[i]);
fscanf(fp1,"%d",&m);
fscanf(fp1,"%f",&x2);
fscanf(fp1,"%f",&x3);
for(i=0;i<n;i++) /*选m个最接近的点*/
c[i]=fabs(x[i]-x2);
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
if(c[i]>c[j]) {t=c[i]; c[i]=c[j]; c[j]=t;
t=x[i]; x[i]=x[j]; x[j]=t;
t=y[i]; y[i]=y[j]; y[j]=t;}
for(i=0;i<m;i++) /*求值*/
{A[i]=1.0;
for(j=0;j<m;j++)
if(i!=j) A[i]=A[i]*(x2-x[j])/(x[i]-x[j]);
z=z+A[i]*y[i];
}
for(i=0;i<m;i++) /*求值*/
{A[i]=1.0;
for(j=0;j<m;j++)
if(i!=j) A[i]=A[i]*(x3-x[j])/(x[i]-x[j]);
z1=z1+A[i]*y[i];
}
fprintf(fp2,"\nx=%10.7f处的函数值为:y=%10.7f",x2,z);
fprintf(fp2,"\nx=%10.7f处的函数值为:y=%10.7f",x3,z1);
fclose(fp1);
fclose(fp2);
}
具体算例及求解结果:
对于一组数据表进行二次数值插值编程,根据下面数值表计算f(0.49)
和f(0.51)

输入数据: 输出结果:
x= 0.4900000处的函数值为:y=18.8637505
4 x= 0.5100000处的函数值为:y=18.3637524
0.2,16
0.4,20
0.6,15
0.8,10
3
0.49
0.51
l 输入变量、输出变量说明:
输入变量: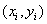 插值节点
插值节点
输出变量: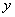 插值所得到被插函数在插值点的近似值
插值所得到被插函数在插值点的近似值
4. 曲线拟合
l 算法原理:
对于给定的一组数据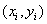 ,
, =1,2…,
=1,2…,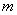 ,寻求做
,寻求做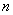 次多项式
次多项式

使性能指标
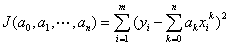 为最小。
为最小。
由于性能指标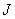 可以被看做关于
可以被看做关于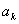 ,
,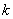 =0,1,…,
=0,1,…,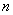 的多元函数,故上述拟合多项式的构造问题可转化为多元函数的极值问题。令
的多元函数,故上述拟合多项式的构造问题可转化为多元函数的极值问题。令
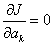
从而有正则方程组
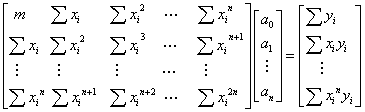
求解即得多项式系数。
l 计算机程序框图:
l 源程序:
#include <math.h>
#include <stdio.h>
main()
{
int i,j,k,m,n,l,N,t,t1;
double max,A[50][50],x[50],y[50],S[50],T[50],X[50];float yb=0.0,xb,a1,a2,a0;
FILE *fp1,*fp2;
fp1=fopen("a4.txt","r");
fp2=fopen("b4.txt","w");
fscanf(fp1,"%d %d\n",&n,&m);
for(i=0;i<n;i++)
{ fscanf(fp1,"%lf %lf",&x[i],&y[i]);
}
fscanf(fp1,"%f",&xb);
for(i=0;i<=2*m;i++)
{S[i]=0.0;
for(j=0;j<n;j++)
S[i]+=pow(x[j],i);
}
for(i=0;i<=m;i++)
{T[i]=0.0;
for(j=0;j<n;j++)
T[i]+=y[j]*pow(x[j],i);
}
N=m+1;
for(i=0;i<N;i++)
{for(j=0;j<N;j++)
{l=i+j;
A[i][j]=S[l];}
A[i][N]=T[i];
}
for(i=0;i<N-1;i++)
{
max=fabs(A[i][i]); /*选主*/
for(j=i+1;j<N;j++)
if(fabs(A[j][i])>max) {max=fabs(A[j][i]); m=j;}
if(m!=i)
for(k=0;k<=N;k++)
{t=A[i][k]; A[i][k]=A[m][k]; A[m][k]=t; }
for(j=i+1;j<N;j++) /*消元*/
for(k=N;k>=0;k--)
A[j][k]=A[j][k]-A[i][k]*A[j][i]/A[i][i];
}
for(i=N-1;i>=0;i--) /*回代*/
for(j=i-1;j>=0;j--)
for(k=N;k>=0;k--)
A[j][k]=A[j][k]-A[i][k]*A[j][i]/A[i][i];
fprintf(fp2,"\n解为:"); /*输出结果*/
for(i=0;i<N;i++)
fprintf(fp2,"\na%d=%10.7lf",i,A[i][N]/A[i][i]);
fprintf(fp2,"\n拟合多项式为:\n");
fprintf(fp2," P(x)=%10.7lf",A[0][N]/A[0][0]);
for(i=1;i<N;i++)
fprintf(fp2,"+(%10.7lf)x^%d",A[i][N]/A[i][i],i);
for(i=0;i<N;i++)
yb+=(A[i][N]/A[i][i])*pow(xb,i);
fprintf(fp2,"\nP(%f)=%10.7f",xb,yb);
fclose(fp1);
fclose(fp2);
}
l 具体算例及求解结果:
对于一组数据表进行二次多项式曲线拟合,根据以下数据胡二次拟合曲线
求y(5)

试用最小二乘法求二次拟合多项式
输入数据: 10 2 输出结果:
1 1.6 解为:
2 2.8 a0=-0.3012450
3 3.6 a1= 1.3167338
4 4.9 a2=-0.0166439
5 5.4 拟合多项式为:
6 6.8 P(x)=-0.3012450+( 1.3167338)x^1+(-0.0166439)x^2
7 7.9 P(5.000000)= 5.8663259
8 9.2
9 10.2
10 11.4
5.0
输入变量、输出变量说明:
输入变量: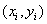 已知数据点
已知数据点
输出变量: 拟合多项式的系数
拟合多项式的系数
5. 改进欧拉法
l 算法原理:
当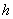 取值较小时,让梯形法的迭代公式只迭代一次就结束。这样先用欧拉公式求得一个初步近似值
取值较小时,让梯形法的迭代公式只迭代一次就结束。这样先用欧拉公式求得一个初步近似值 ,称之为预报值,预报值的精度不高,用它替代梯形法右端的
,称之为预报值,预报值的精度不高,用它替代梯形法右端的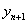 ,再直接计算得出
,再直接计算得出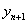 ,并称之为校正值,这时得到预报-校正公式。将预报-校正公式
,并称之为校正值,这时得到预报-校正公式。将预报-校正公式
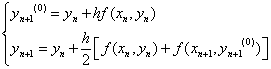
称为改进欧拉公式。
l 计算机程序框图:
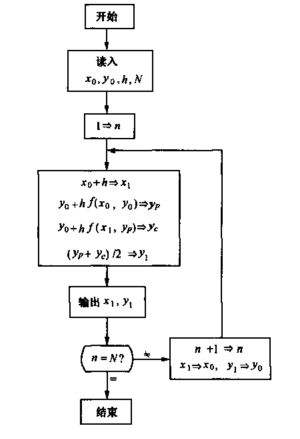
l 源程序:
#include "stdio.h"
#include "math.h"
FILE *fp1,*fp2;
float func(float x,float y)
{float dy;
dy=sqrt(2*x*x+3*y*y);
return (dy); /*定义函数的导*/
}
main()
{int i;
float h,yp,yc,y0,x1,x2;
if((fp1=fopen("a5.txt","r"))==NULL)
{printf("cannot open this file\n");
exit(0);}
fp2=fopen("b5.txt","w");
fscanf(fp1,"%f,%f,%f,%f",&x1,&x2,&y0,&h);
for(i=0;i<(x2-x1)/h;i++)
{yp=y0+h*func(x1+i*h,y0);
yc=y0+h*func(x1+(i+1)*h,yp);
y0=0.5*(yp+yc);
fprintf(fp2,"节点%6.2f处的值=%10.7f\n",x1+(i+1)*h,y0);
}
fclose(fp1);
fclose(fp2);
l }
l 具体算例及求解结果:
求解初值问题。取h=0.2,用改进欧拉法求解下列初值问题
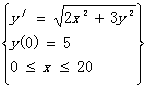
输入数据:0,20,5,0.2 输出结果 节点 0.20处的值= 7.0323939
节点 0.40处的值= 9.8918471 节点 0.60处的值=13.9148121
节点 0.80处的值=19.5739155 节点 1.00处的值=27.5336847
节点 1.20处的值=38.7287178 节点 1.40处的值=54.4735222
节点 1.60处的值=76.6169243 节点 1.80处的值=107.7592354
节点 2.00处的值=151.5576096 节点 2.20处的值=213.1555939
节点 2.40处的值=299.7871094 节点 2.60处的值=421.6261139
节点 2.80处的值=592.9812927 节点 3.00处的值=833.9766235
节点 3.20处的值=1172.9145508 节点 3.40处的值=1649.6000366
节点 3.60处的值=2320.0151367 节点 3.80处的值=3262.8935547
节点 4.00处的值=4588.9670410 节点 4.20处的值=6453.9699707
节点 4.40处的值=9076.9287109 节点 4.60处的值=12765.8852539
节点 4.80处的值=17954.0703125 节点 5.00处的值=25250.7871094
节点 5.20处的值=35512.9648438 节点 5.40处的值=49945.7949219
节点 5.60处的值=70244.2773438 节点 5.80处的值=98792.2734375
节点 6.00处的值=138942.4609375 节点 6.20处的值=195410.0937500
节点 6.40处的值=274826.7343750 节点 6.60处的值=386519.1406250
节点 6.80处的值=543604.4218750 节点 7.00处的值=764530.8125000
节点 7.20处的值=1075243.9062500节点 7.40处的值=1512233.8750000
节点 7.60处的值=2126821.1875000 节点 7.80处的值=2991183.0000000
节点 8.00处的值=4206830.1250000 节点 8.20处的值=5916528.2500000
节点 8.40处的值=8321065.2500000 节点 8.60处的值=11702831.0000000
节点 8.80处的值=16458980.5000000 节点 9.00处的值=23148077.0000000
节点 9.20处的值=32555688.0000000 节点 9.40处的值=45786650.0000000
节点 9.60处的值=64394808.0000000 节点 9.80处的值=90565512.0000000
节点0.00处的值=127372260.0000000 节点 10.20处的值=179137632.0000000
节点10.40处的值=251940992.0000000 节点10.60处的值=354332368.0000000
节点 10.80处的值=498336624.0000000 节点11.00处的值=700865696.0000000
节点 11.20处的值=985704608.0000000节点11.40处的值=1386304896.0000000
节点 11.60处的值=1949713344.0000000 节点 11.80处的值=2742096640.000000012.00处的值=3856512512.0000000 节点 12.20处的值=5423838208.0000000
节点 12.40处的值=7628141056.0000000 节点 12.60处的值=10728294912.0000000节点 12.80处的值=15088381952.0000000
节点 13.00处的值=21220453376.0000000节点13.20处的值=29844662272.0000000节点 13.40处的值=41973835776.0000000
节点 13.60处的值=59032424448.0000000节点 13.80处的值=83023802368.0000000节点 14.00处的值=116765528064.0000000
节点 14.20处的值=164220223488.0000000节点 14.40处的值=230960996352.0000000节点 14.60处的值=324825874432.0000000
节点 14.80处的值=456838414336.0000000节点 15.00处的值=642502164480.0000000节点 15.20处的值=903621574656.0000000
节点 15.40处的值=1270862577664.0000000节点 15.60处的值=1787354021888.0000000节点 15.80处的值=2513752817664.0000000
节点 16.00处的值=3535367438336.0000000节点 16.20处的值=4972176474112.0000000 节点 16.40处的值=6992919527424.0000000
节点 16.60处的值=9834913071104.0000000 节点 16.80处的值=13831921729536.0000000 节点 17.00处的值=19453354967040.0000000
节点 17.20处的值=27359394660352.0000000 节点 17.40处的值=38478530215936.0000000 节点 17.60处的值=54116592123904.0000000
节点 17.80处的值=76110125596672.0000000 节点 18.00处的值=107042052243456.0000000 节点 18.20处的值=150545029398528.0000000
节点 18.40处的值=211728063266816.0000000 节点 18.60处的值=297776508305408.0000000 节点 18.80处的值=418795919245312.0000000
节点 19.00处的值=588998829408256.0000000 节点 19.20处的值=828373899149312.0000000 节点 19.40处的值=1165033501360128.0000000
节点 19.60处的值=1638514923929600.0000000 节点 19.80处的值=2304424236023808.0000000 节点 20.00处的值=3240965678563328.0000000
输入变量、输出变量说明:
输入变量: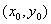 处置点,
处置点,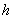 区间长度,
区间长度,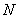 计算次数
计算次数
输出变量: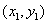 初值问题的数值解法结果
初值问题的数值解法结果
6. 四阶龙格-库塔法
l 算法原理:
用区间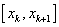 内四个不同点上的函数值的线性组合就得到四阶龙格-库塔法。
内四个不同点上的函数值的线性组合就得到四阶龙格-库塔法。
四阶龙格-库塔法
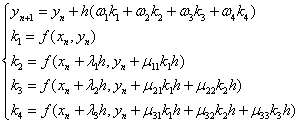
其中,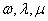 均为待定系数。
均为待定系数。
类似于前面的讨论,把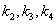 分别在
分别在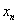 点展开成
点展开成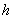 的幂级数,代入
的幂级数,代入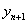 并进行花间,然后与
并进行花间,然后与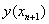 在
在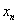 点上的泰勒展开式比较,使其两式比较,使其两式右端直到
点上的泰勒展开式比较,使其两式比较,使其两式右端直到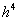 的系数相等,经过复杂的数学演算可得到关于
的系数相等,经过复杂的数学演算可得到关于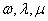 的一组特解
的一组特解
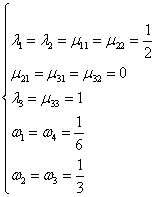
从而得到下列常用的经典公式
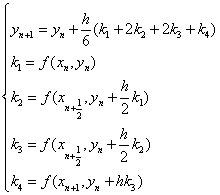
经典的龙格-库塔法每一步需要4次计算函数值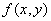 ,它具有四阶精度,即局部截断误差是
,它具有四阶精度,即局部截断误差是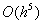 。
。
l 计算机程序框图:
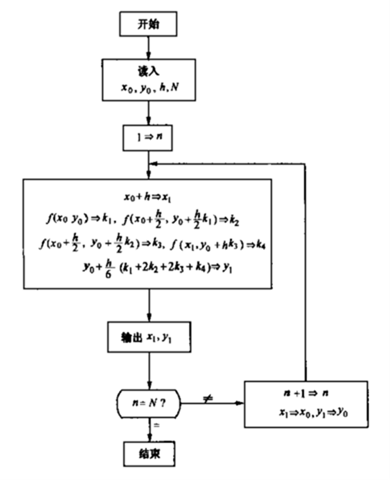
源程序:#include "stdio.h"
#include "math.h"
FILE *fp1,*fp2;
float ds(float x,float y)
{
float d;
d=sqrt(x*x+y*y);
return d;
}
void main()
{
int i;
float x[101],y[101],h,b,k1,k2,k3,k4;
if((fp1=fopen("a6.txt","r"))==NULL)
{printf("cannot open this file\n");
exit(0);}
fp2=fopen("b6.txt","w");
fscanf(fp1,"%f,%f,%f,%f",&h,&x[0],&b,&y[0]);
for(i=1;i<=100;i++)
if((x[0]+i*h)<=b+h)
{x[i]=x[0]+i*h;
k1=ds(x[i-1],y[i-1]);
k2=ds(x[i-1]+h/2,y[i-1]+h*k1/2);
k3=ds(x[i-1]+h/2,y[i-1]+h*k2/2);
k4=ds(x[i],y[i-1]+h*k3);
y[i]=y[i-1]+h*(k1+2*k2+2*k3+k4)/6.0;
}
else break;
for(i=0;i<=100;i++)
if((x[0]+i*h)<=b+h)
{x[i]=x[0]+i*h;
fprintf(fp2,"\n%10.5f点处的值=%10.7f",x[i],y[i]);}
else break;
fclose(fp1);
fclose(fp2);
}
具体算例及求解结果:
求解初值问题,取h=0.2,用四阶 龙格-库塔法求解下列初值问题

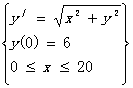
输入数据:0.2,0,20,6
输出结果: 0.00000点处的值= 6.0000000 0.20000点处的值= 7.3286018
0.40000点处的值= 8.9523811 0.60000点处的值=10.9372101
0.80000点处的值=13.3631592 1.00000点处的值=16.3277931
1.20000点处的值=19.9501495 1.40000点处的值=24.3755608
1.60000点处的值=29.7815247 1.80000点处的值=36.3848495
2.00000点处的值=44.4503784 2.20000点处的值=54.3016205
2.40000点处的值=66.3337555 2.60000点处的值=81.0294876
2.80000点处的值=98.9784317 3.00000点处的值=120.9007721
3.20000点处的值=147.6761780 3.40000点处的值=180.3790741
3.60000点处的值=220.3218079 3.80000点处的值=269.1072998
4.00000点处的值=328.6933289 4.20000点处的值=401.4711609
4.40000点处的值=490.3615112 4.60000点处的值=598.9317017
4.80000点处的值=731.5388794 5.00000点处的值=893.5048828
5.20000点处的值=1091.3298340 5.40000点处的值=1332.9528809
5.60000点处的值=1628.0709229 5.80000点处的值=1988.5278320
6.00000点处的值=2428.7895508 6.20000点处的值=2966.5251465
6.40000点处的值=3623.3151855 6.60000点处的值=4425.5185547
6.80000点处的值=5405.3295898 7.00000点处的值=6602.0703125
7.20000点处的值=8063.7695313 7.40000点处的值=9849.0888672
7.60000点处的值=12029.6777344 7.80000点处的值=14693.0488281
8.00000点处的值=17946.0898438 8.20000点处的值=21919.3554688
8.40000点处的值=26772.3007813 8.60000点处的值=32699.6894531
8.80000点处的值=39939.4023438 9.00000点处的值=48781.9882813
9.20000点处的值=59582.3203125 9.40000点处的值=72773.8437500
9.60000点处的值=88885.9765625 9.80000点处的值=108565.3359375
10.00000点处的值=132601.7031250 10.20000点处的值=161959.7187500
10.40000点处的值=197817.5937500 10.60000点处的值=241614.4062500
10.80000点处的值=295107.8437500 11.00000点处的值=360444.7187500
11.20000点处的值=440247.1875000 11.40000点处的值=537717.9375000
11.60000点处的值=656768.6875000 11.80000点处的值=802177.2500000
12.00000点处的值=979779.3125000 12.20000点处的值=1196702.5000000
12.40000点处的值=1461652.3750000 12.60000点处的值=1785262.2500000
12.80000点处的值=2180519.2500000 13.00000点处的值=2663286.2500000
13.20000点处的值=3252937.7500000 13.40000点处的值=3973138.2500000
13.60000点处的值=4852791.0000000 13.80000点处的值=5927199.0000000
14.00000点处的值=7239481.0000000 14.20000点处的值=8842302.0000000
14.40000点处的值=10799988.0000000 14.60000点处的值=13191105.0000000 14.80000点处的值=16111616.0000000 15.00000点处的值=19678728.0000000 15.20000点处的值=24035598.0000000 15.40000点处的值=29357080.0000000 15.60000点处的值=35856736.0000000 15.80000点处的值=43795416.0000000 16.00000点处的值=53491720.0000000 16.20000点处的值=65334788.0000000 16.40000点处的值=79799912.0000000 16.60000点处的值=97467616.0000000 16.80000点处的值=119046944.0000000 17.00000点处的值=145403936.0000000
17.20000点处的值=177596368.0000000 17.40000点处的值=216916208.0000000 17.60000点处的值=264941456.0000000 17.80000点处的值=323599488.0000000 18.00000点处的值=395244416.0000000
18.20000点处的值=482751520.0000000 18.40000点处的值=589632704.0000000 18.60000点处的值=720177408.0000000 18.80000点处的值=879624704.0000000 19.00000点处的值=1074373632.0000000
19.20000点处的值=1312240000.0000000 19.40000点处的值=1602769920.0000000 19.60000点处的值=1957623168.0000000 19.80000点处的值=2391041024.0000000 20.00000点处的值=2920417536.0000000
l 输入变量、输出变量说明:
输入变量: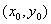 处置点,
处置点,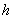 区间长度,
区间长度,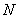 计算次数
计算次数
输出变量: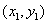 初值问题的数值解法结果
初值问题的数值解法结果
二、 上机体验与收获
首先,是程序的编制过程中,我体会到了将一个抽象的数值计算方法变为一个具体计算机程序的不易。这个过程,让我对各种数值计算方法的数学公式有了更进一步的认识,因为要编制出计算机程序,就必须清楚数值计算方法的具体计算步骤。并且这次我还补充了自己的C语言知识,学会了C语言中文件的操作,这一部分内容在原先的C语言课程中式没有讲述过的。在各个程序的调试过程中,我又重新复习C语言的很多知识,比如数组元素的编号以及数组行列的编号都是从0开始的等。数值计算方法编程过程中涉及到了许多循环结构,这很好的锻炼了我的数学思维。
有所遗憾的是,尽管我努力的学习了编程,但是由于水平有限,仍不能编制出一个较为完整的程序,所以这里大多数的程序都是参考于别处。但是每一个我都进行了认真的调试和细微入致的理解,很好把握了每个程序的思想,为我以后能合适的应用数值计算方法奠定了基础。
其次,我要说的事此次试验报告的写作,运用了Mathtype在Word里面编辑了如此多的数学公式,让我对运用Mathtype进行数学公式编辑以及Word排版都有了新的认识。实践的过程总是会遇到各种各样的问题,但经过努力钻研并获得知识是快乐的,这就是我的体会。
