天津师范大学
本科毕业论文(设计)
题目:归纳法与数学归纳法
学 院:数学科学学院
学生姓名:王珏
学 号:03505024
专 业:数学与应用数学
年 级:20##级
完成日期:20##-5
指导教师:沈佩真
归纳法与数学归纳法
摘要:归纳就是从特殊的、具体的认识推进到一般的认识的一种思维方式.归纳法是一种从特殊到一般的推理方法,即通过对研究对象的若干特殊情况的考察分析而得到关于一般情形结论的推理方法.归纳法分为完全归纳法和不完全归纳法.而数学归纳法是归纳与演绎的结合体,与通常的归纳法有本质的区别.它是一种论证方法,通常上用来证明数学上的猜想,而这种猜想是用某种归纳法所获得的.数学归纳法的理论依据是归纳公理.
关键字:归纳,猜想,归纳法,数学归纳法
The Induction and the Mathematical Induction
Abstract: The induction is one thinking mode which is from special, concrete understanding advances to the general understanding. The induction is a kind of method from special to the general inference, through obtains to the object of study certain peculiar circumstance inspection analysis about the general situation conclusion inference method. The induction divides into the complete induction and incomplete induction. But the mathematical induction is ties the synthesis of induction and deductive, has the essential difference with the usual induction. It is a proof method, usually uses for to prove in mathematics the suspicion, but this kind of suspicion is obtains with some induction. The mathematical induction theory basis induces the axiom.
Key words: Induce, Guess, Induction, Mathematical induction
目 录
一、归纳……………………………………………………………………………………(1)
(一)归纳的定义………………………………………………………………………(1)
(二)归纳的步骤………………………………………………………………………(1)
二、归纳法…………………………………………………………………………………(1)
(一)归纳法的定义……………………………………………………………………(1)
1.等周定理的内容 …………………………………………………………………(2)
2.等周定理的证明 …………………………………………………………………(2)
(二)归纳法的特点……………………………………………………………………(4)
(三)归纳法的分类……………………………………………………………………(4)
1.完全归纳法 ………………………………………………………………………(4)
2.不完全归纳法 ……………………………………………………………………(5)
三、数学归纳法……………………………………………………………………………(7)
(一)数学归纳法的历史………………………………………………………………(7)
(二)数学归纳法的理论依据…………………………………………………………(8)
(三)数学归纳法的步骤………………………………………………………………(9)
四、归纳法与数学归纳法的联系与区别…………………………………………………(10)
参考文献 …………………………………………………………………………………(12)
一、归纳
(一) 归纳的定义
就人类认识的程序而言,总是先认识某些特殊的现象,然后过渡到一般的现象.归纳就是从特殊的、具体的认识推进到一般的认识的一种思维方式.玻利亚在《数学与猜想》中认为归纳是指从特殊例子推出一般规律或者从提出事实到证明一般命题的过程.
(二) 归纳的步骤
明显的,两者都认为归纳是一个过程,而且波利亚又明确地提出这一过程的典型步骤:
注意到某些相似性——把相似性推广为明确表达的一般命题——检验一般性命题
上面的过程即归纳的一般模式:

归纳能力具体表现为①从特殊和具体的事物中发现某些一般的,主体已经知道了的东西的能力,即特例纳入一个已知一般概念的能力;②从孤立和特殊的事物中看出某些一般的,主体尚未知道的东西的能力,即从一些特例推演出一般,并形成一般概念的能力.
归纳的过程实际上是一个思想的适应、语言的适应的过程.归纳过程是把我们的思想认识适应于事实的结果.每当我们的想法和观察相比较时,其结果可能一致也可能不一致.若与观察事实一致,我们就对我们的想法更有信心;若不一致,我们就改变想法.经过多次改变之后,我们的想法就较好的符合事实.我们对任何新事物的想法,开头总不免是错误或者至少有一部分是错误的,归纳过程(总结经验)就提供了改正错误的机会,使思想符合现实.所以归纳的主要作用是探索化归的方向和目标,发现问题的结论,寻求解决问题的途径.
二、归纳法
(一) 归纳法的定义
归纳法,是一种从特殊到一般的推理方法,即通过对研究对象的若干特殊情况的考察分析而得到关于一般情形结论的推理方法.由于事物的普遍性寓于事物的特殊性之中,人们对数学的认识,开始时常常从特殊的情况入手,去探索和发现一般的普遍
性的规律,因此,归纳法是数学探索发现的一种重要方法.著名的数学家高斯说过,他的许多定理都是靠归纳法发现的.下面我们通过在数学发展史上占有重要地位的等周问题的认识及证明过程来感受一下归纳法在实际应用中的重要作用.
1.等周定理的内容
笛卡尔有一部未完成的著作《思想的法则》,这是一本讲如何发现的经典著作.书中有这样一段重要的话:“为了用列举法证明圆的周长比任何具有相同面积的其他图形的周长都小,我们不必考察全部所有可能的图形,只需对几个特殊的图形进行证明,结合运用归纳法,就可以得到与对所有其他图形都进行证明得出同样的结论.”
为了理解笛卡尔的这段话,我们来考察一部份图形,并假定它们有相同的面积,例如一平方寸.下表给出相同面积的图形的周长:

所列10个图形具有相同的面积,圆具有最短的周长.这个列表强有力地暗示出一个一般的定理:在所有图形中,圆具有最短周长.说它强有力,是因为再在表中增加一个或两个以上的图形,也增加不了多少启发性.这正是笛卡尔的话的精华所在.
定理1(等周定理)具有相等面积的所有图形中,圆具有最小的周长.
古人认为,圆是最完美的图形.这句话还含有深刻的数学意义.
通过类比,我们还能得到空间等周定理.
定理2(空间等周定理)具有相等体积的所有立体图形中,球具有最小的表面积.
2.等周定理的证明
等周定理还可换一种说法:在周长固定的情况下,圆具有最大的面积,下面的证明就采用这种表达方式.为证明等周定理,我们首先需要一个关于三角形面积的定理.
定理3 给定两条线段a和b,以a和b为边的所有三角形中,以a和b为直角边的直角三角形具有最大面积.
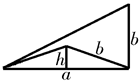
图1
证明:如图1所示,考虑一个以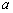 和
和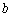 为边的任意三角形.如果
为边的任意三角形.如果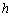 是底边
是底边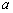 上的高,那么这个三角形的面积是
上的高,那么这个三角形的面积是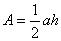 ,显然,
,显然,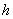 取最大值时,
取最大值时,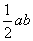 也最大,这只有当
也最大,这只有当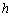 和
和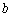 重合时才能发生,而这时就是一个直角三角形.最大面积是
重合时才能发生,而这时就是一个直角三角形.最大面积是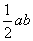 .
.
在证明等周定理之前,我们先讲一讲什么叫曲线.在曲线上任取两点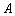 、
、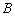 ,如果连接
,如果连接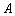 、
、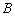 的线段
的线段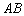 全部落在曲线上,或在曲线围成的区域的内部,则称这条曲线是凸的(图2),圆和椭圆都是凸曲线.图3所示的曲线就不是凸曲线.
全部落在曲线上,或在曲线围成的区域的内部,则称这条曲线是凸的(图2),圆和椭圆都是凸曲线.图3所示的曲线就不是凸曲线.
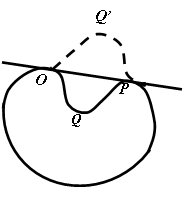
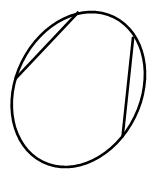
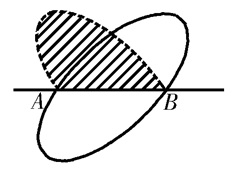
图2 图3 图4
平面等周定理的证明:设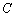 是周长
是周长 一定的所有闭曲线中围成最大面积的那条闭曲线.
一定的所有闭曲线中围成最大面积的那条闭曲线.
首先证明,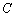 一定是凸曲线.否则,在
一定是凸曲线.否则,在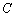 上一定可以找到一对点
上一定可以找到一对点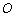 和
和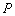 ,使线段
,使线段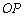 在
在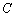 外.这时以
外.这时以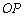 为轴,把曲线
为轴,把曲线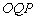 反射到另一侧成为曲线
反射到另一侧成为曲线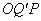 (图3).弧
(图3).弧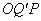 与弧
与弧 一起形成长度为
一起形成长度为 的一条曲线,而它包含的面积比原曲线
的一条曲线,而它包含的面积比原曲线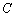 包含的面积大.但这与长度为
包含的面积大.但这与长度为 的闭曲线
的闭曲线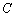 含有最大面积的假设相矛盾.所以
含有最大面积的假设相矛盾.所以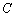 一定是曲线.
一定是曲线.
现在选取两点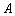 和
和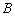 ,把曲线
,把曲线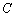 分割为长度相等的两段弧,这时直线
分割为长度相等的两段弧,这时直线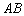 也必将
也必将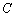 所围成的面积分割为两个相等的部分;因为不然的话,可以把较大的那部分对
所围成的面积分割为两个相等的部分;因为不然的话,可以把较大的那部分对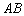 作反射,就得到另一条长度为
作反射,就得到另一条长度为 、比
、比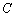 围有更大面积的曲线了(图4).
围有更大面积的曲线了(图4).
这样一来,问题转化为:求长度为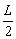 的弧,其端点
的弧,其端点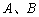 在一条直线上,它与这条直线围成的面积为最大,我们来证明这个问题的解是半圆,从而等周问题的解
在一条直线上,它与这条直线围成的面积为最大,我们来证明这个问题的解是半圆,从而等周问题的解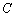 是一个圆.
是一个圆.
设弧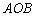 (图5)是新问题的解,这只要证明每一个内接角,例如图5的
(图5)是新问题的解,这只要证明每一个内接角,例如图5的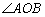 是直角就行了,因为这就证明了弧
是直角就行了,因为这就证明了弧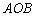 是半圆.我们用反证法来证明.假定
是半圆.我们用反证法来证明.假定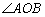 不是直角,那么我们用图6的图形代替图形5.在这个新图形中阴影部分的面积和弧
不是直角,那么我们用图6的图形代替图形5.在这个新图形中阴影部分的面积和弧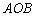
的长度都没有改变,而由于使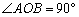 ,三角形的面积增大了.这样,图6比原图有更大的面积.这与假设相矛盾.这个矛盾证明了对任意点
,三角形的面积增大了.这样,图6比原图有更大的面积.这与假设相矛盾.这个矛盾证明了对任意点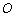 ,
,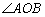 必是直角.
必是直角.
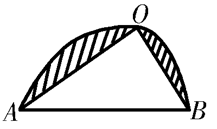
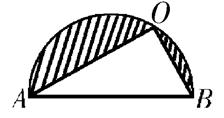
图5 图6
等周性质还可以用一个不等式来表示.设 是圆的周长,则它的面积为
是圆的周长,则它的面积为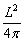 .根据等周定理,长度为
.根据等周定理,长度为 的任意闭曲线和它所围成的面积
的任意闭曲线和它所围成的面积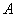 必然满足不等式
必然满足不等式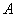
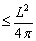 .这个不等式叫做等周不等式.
.这个不等式叫做等周不等式.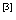
(二) 归纳法的特点:
1.归纳的前提是单个的事实或特殊的情况,所以,归纳立足于观察和实验,其结论未必可靠.
2.归纳是依据若干已知的、不完备的现象推断未知的现象,因而结论具有猜测的性质.
3.归纳是从特殊现象去推断一般现象,因此,由归纳所得的结论超越了前提所包含的内容.
(三)归纳法的分类
归纳法又分为完全归纳法和不完全归纳法两种,下面分别说明这两种归纳法在数学探索和发现中的应用.
1.完全归纳法
如果对研究对象的所有各种特殊情况分别加以分析之后,进而得出关于一般情形的结论,那么就称这种归纳法为完全归纳法. 由于完全归纳法已经考察了所有特殊情况,所以只要推理的各个前提是真的又遵循推理的各项规则,那么得到的一般结论必定是真的.因此,完全归纳法是一种严格的必真推理方法.应用完全归纳法探索数学问题的关键在于对所研究对象的所有各种情况进行正确而适当的分类.正确分类是指必须遵循分类的基本规则,不遗漏不重复等;适当分类是指必须根据所研究问题的特点,选择适合这种特点的具体分类标准进行逐级分类等等.
例1把一张任意形状的纸紧贴在桌面上(平面),问是否一定能在纸的边界线上找
出四点共圆?
分析:因为平面上纸的边界线是封闭曲线(也可以含折线),所以在这边界线上至少有三点不共线,不妨设这三点为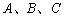 .过这不共线三点可作一圆
.过这不共线三点可作一圆 (圆心为
(圆心为 ),这三点把纸边界线分成三段曲线
),这三点把纸边界线分成三段曲线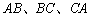 .分类讨论如下;(一)若这三段曲线中,除端点外,还有第四点
.分类讨论如下;(一)若这三段曲线中,除端点外,还有第四点 也在圆
也在圆 上,则
上,则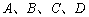 四点共圆.(二)若这三段曲线中,除端点外,再没有任何点在圆
四点共圆.(二)若这三段曲线中,除端点外,再没有任何点在圆 上,则由抽屉原则,这三段曲线中(除瑞点外)至少有两段同在圆
上,则由抽屉原则,这三段曲线中(除瑞点外)至少有两段同在圆 外部或至少有两段同在圆
外部或至少有两段同在圆 内部,再进行二级分类讨论如下:(1)若至少有两段同在圆
内部,再进行二级分类讨论如下:(1)若至少有两段同在圆 外部,则分别在这两段曲线(除端点外)上各取两点
外部,则分别在这两段曲线(除端点外)上各取两点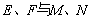 .设
.设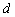 = min {
= min {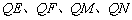 } 以
} 以 为圆心,
为圆心,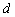 为半径作圆必交这两段曲线于四点,则这四点共圆.(2)若至少有两段同在圆
为半径作圆必交这两段曲线于四点,则这四点共圆.(2)若至少有两段同在圆 内部,则分别在这两段曲线上(除端点外)各取两点,设这四点与
内部,则分别在这两段曲线上(除端点外)各取两点,设这四点与 的距离最大者为
的距离最大者为 ,以
,以 为圆心,
为圆心, 为半径作圆必交这两段曲线于四点,则这四点共圆.
为半径作圆必交这两段曲线于四点,则这四点共圆.
由以上所有各种情况分类讨论的结果,可归纳出一般结论:在这纸的边界线上可找到四点共圆.
中学数学中的许多定理,如圆周角定理、正弦定理等都是用完全归纳法推出来的.
2.不完全归纳法
如果仅对研究对象的一些而不是所有的特殊情况进行考察分析,就得出关于一般情况的结论,那么称这种归纳法为不完全归纳法,其所得到的一般结论,仅是一个猜想,正确与否还要经过严格的推理论证,因此,不完全归纳法是一种似真推理方法.例如,法国数学家费马曾根据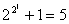 ,
,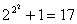 ,
, 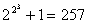 ,
, ,都是素数,用不完全归纳法得出如下猜想:“任何形如
,都是素数,用不完全归纳法得出如下猜想:“任何形如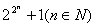 的数都是素数” .但半个世纪之后,欧拉却发现
的数都是素数” .但半个世纪之后,欧拉却发现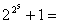 4294967297
4294967297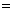 641
641 6700417并不是素数,推翻了费马猜想.
6700417并不是素数,推翻了费马猜想.
不完全归纳法虽不是必真推理方法,但它对数学发展却具有重要意义.最著名的例子就是被誉为数学皇冠上明珠的哥德巴赫猜想,哥德巴赫根据6=3+3,8=5+3,10=7+3,12=7+5,14=7+7,16=13+3,18=11+7,20=13+7… ,用不完全归纳法得到猜想:“任何大于4的偶数都可表示成两个奇素数之和” .这猜想至今尚未得到最后的证明,也未找到反例.而二百多年来,人们对这猜想的研究却极大地推动了数论的发展,我国著名的数学家陈景润在这一方面的研究,取得了世界领先的成果.
数论中“四方定理”的发现,也是成功地应用不完全归纳法的例子.至少要用多少个平方数之和才能保证表示一个任意的自然数?巴切特用不完全归纳法进行了探索: 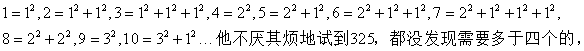
于是他猜想:“任何自然数,或者本身是平方数,或者是两个或三个或四个平方数的和”.这个猜想被称为“四方定理”.
应用不完全归纳法进行数学探索和发现的基本步骤是:
(1) 从具体数学问题出发,先对部分较简的特殊情况进行观察实验;
(2) 归纳出其中的规律;
(3) 推广到一般情况,提出猜想,形成普遍的命题;
(4)证明这猜想正确与否.
例 2 设数列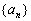 与
与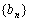 的通项分别为
的通项分别为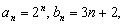 它们的公共项由小到大排成数列
它们的公共项由小到大排成数列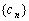 .求
.求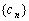 的前n 项之和.
的前n 项之和.
分析: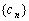 是什么样的数列,题中没有直接指明,可用不完全归纳法先考察,
是什么样的数列,题中没有直接指明,可用不完全归纳法先考察, 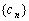 的前几项.由条件可知,凡属
的前几项.由条件可知,凡属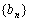 的项,以3除必余2, 依次写出的
的项,以3除必余2, 依次写出的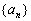 项,用此原则去考察(属于
项,用此原则去考察(属于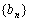 的项底下加横线),有
的项底下加横线),有
2,4,8,16,32,64,128, 256,512, 1024,2048
所以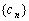 的前五项为8,32,128,512,2048,归纳其规律是首项为8,公比为4 的等比数列.由此推广猜测:
的前五项为8,32,128,512,2048,归纳其规律是首项为8,公比为4 的等比数列.由此推广猜测: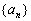 从第3项起,其奇数项组成
从第3项起,其奇数项组成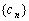 ,
,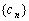 是首项为8,公比为4 的等比数列.
是首项为8,公比为4 的等比数列.
解:由己知可得: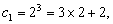 设
设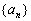 的第
的第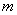 项与
项与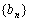 的第
的第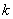 顶相等,并设这是
顶相等,并设这是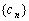 的第
的第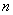 项,即
项,即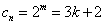 .因为
.因为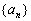 是递增的,它的第
是递增的,它的第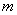 +1项为
+1项为 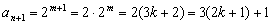 , 不是
, 不是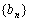 的项 : 而
的项 : 而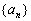 的第
的第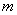 +2项为
+2项为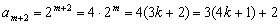 是
是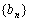 的项,从而也是
的项,从而也是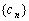 的第
的第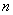 +1项,即
+1项,即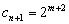 , 由此可见,
, 由此可见,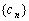 是首项为8,公比为4的等比数列,其前
是首项为8,公比为4的等比数列,其前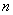 项之和为
项之和为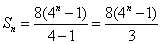 .
.
从以上例子可看出,应用不完全归纳法项为探索教学问题时,常常先从特殊情况入手,把对特殊情况分析结果作为基础,再推广到一般情况;或从对特殊情况的研究过程中,找到解决问题的关键方法途径,再用以解决一般情况下的问题.
上述步骤可简单表示如下:观察实验——归纳——推广——证明.其中不完全归纳法主要体现在前三个步骤中,推广形成普遍命题之后的证明工作,则要借助于其它严格的数学证明方法.如演绎法、数学归纳法等等.
最后必须强调指出,在数学的探索发现过程中,应把归纳法与其它的数学研究方
法, 如演绎、类比、分析、综合、转化、比较、联想、直觉、抽象等等诸多的方法紧密结合起来,才能取得最佳效果.
三、数学归纳法
(一)数学归纳法的历史
数学归纳法最先由意大利数学家莫罗利科(Maurolycus,1494~1575)提出,后经法国数学家帕斯卡(Pascal,1623~1662)进一步完善,最终由意大利数学家皮亚诺(Peano,1858~1932)奠定了逻辑基础,这是人们公认的数学归纳法的历史.事实上,早在古希腊的欧几里德(Eulid,公元前300年)时代,数学归纳法的思想就有所萌芽.他在证明素数个数无穷时,就认为:若有n个素数,就必有n+1个素数;既有第一个素数,素数个数必无穷.尽管他论证过程中的递归推理不甚明显,但基本上是按照递归推理原理指导的.欧几里德以后,递归思想曾在级数求和等问题上得到过应用,遗憾的是没有人明确的提出这个方法,直到一千多年后才由莫罗利科提出来.数学归纳法这一专业术语,是英国数学家德摩根(DeMor2gan,1806~1871)于1838年在他的小百科全书中提出并延用至今的.正是由于这一名称,有人认为该方法是归纳的方法.其实数学归纳法是演绎推理,这是由其实质所决定的.
首先,数学归纳法是证明的公式.证明与自然数有关的命题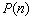 :(1)证明
:(1)证明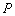 (1)
(1)
真;(2)假设 真,证明
真,证明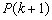 也真.若(1)、(2)都得证,则对一切自然数
也真.若(1)、(2)都得证,则对一切自然数 ∈
∈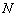 ,
,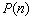 都真,其中(1)是奠基,没有它论证就没有可靠性,就可能谬种流传;(2)是递推,没有它论证就没有准确性,就可能一叶障目.这两个步骤相互作用,缺一不可,构成和谐统一的演绎公式:
都真,其中(1)是奠基,没有它论证就没有可靠性,就可能谬种流传;(2)是递推,没有它论证就没有准确性,就可能一叶障目.这两个步骤相互作用,缺一不可,构成和谐统一的演绎公式: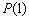 ∧
∧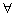 k(
k( →
→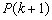 )
)
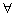

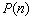 .庞加莱(Poincare,1854~1912)赞誉它是将无穷的三段论纳入唯一的公式中,波利亚(GeorgePolya,1887~1985)称它为从
.庞加莱(Poincare,1854~1912)赞誉它是将无穷的三段论纳入唯一的公式中,波利亚(GeorgePolya,1887~1985)称它为从 推到
推到 +1的方法,这都深刻地指明了数学归纳法的实质是递归推理,是证明的方法.
+1的方法,这都深刻地指明了数学归纳法的实质是递归推理,是证明的方法.
其次,数学归纳法是归纳与演绎的结合体,与通常的归纳法有本质的区别.归纳法是寻求结论的手段,对结论只能作出合乎情理的猜想或假说,其结论不是必然的.如“素数公式”: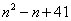 ,结论对
,结论对 =1,2,…,40都是正确的,能否断言对一切自然数都成立?不能!因为当
=1,2,…,40都是正确的,能否断言对一切自然数都成立?不能!因为当 =41时公式给出的412就不是素数了.而数学归纳法就不同了,其实质是递归推理,隐含着推向无穷的可能,两个步骤又确保了论证的严密性和准确性,因而数学归纳法既不同于不完全归纳法也不同于完全归纳法.然而,数学归纳法与通常的归纳法仍有相似之处,有一个从个别、特殊到普遍、一般的归纳形式,而且是以皮亚诺的“归纳公理”为基础的.从这个意义上讲数学归纳法有归纳的成份,可以说是归纳与演绎“协同作战”的样板.
=41时公式给出的412就不是素数了.而数学归纳法就不同了,其实质是递归推理,隐含着推向无穷的可能,两个步骤又确保了论证的严密性和准确性,因而数学归纳法既不同于不完全归纳法也不同于完全归纳法.然而,数学归纳法与通常的归纳法仍有相似之处,有一个从个别、特殊到普遍、一般的归纳形式,而且是以皮亚诺的“归纳公理”为基础的.从这个意义上讲数学归纳法有归纳的成份,可以说是归纳与演绎“协同作战”的样板.
再次,数学归纳法常与归纳法联合使用,是归纳法的“数学补充”.归纳常用于猜想,而数学归纳法却是用于证明的,在科学发现中常“作为归纳性研究的终结步骤或最后阶段出现,而这最后阶段又常常从上面叙述的各个阶段中得到启发.”(波利亚语)事实上,“归纳——猜想——证明”是解决数学问题常用的策略.
最后,数学归纳法也有其局限性.一方面数学归纳法只能证明现成的公式或给定的结论,在科学发现中只能充当补证的角色,它本身不会发现或导出结论;另一方面数学归纳法是证明有关自然数命题常用的有效的方法,但并不意味着一切与自然数有关的命题都可以用数学归纳法求证,或用它来证比较方便.
(二)数学归纳法的理论依据
数学归纳法的理论依据是下列归纳公理:
(1)存在一个自然数0∈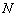 .
.
(2)每个自然数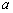 有一个后继元素
有一个后继元素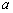 ',如果
',如果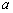 '是
'是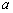 的后继元素,则
的后继元素,则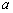 叫做
叫做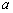 '的生成元素.
'的生成元素.
(3)自然数0无生成元素.
(4)如果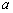 '=
'=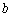 ',则
',则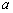 =
=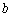 .
.
(5)(归纳公理)自然数集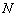 的每个子集合
的每个子集合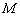 ,如果
,如果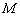 含有0,并且含有
含有0,并且含有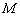 内每个元素的后继元素,则
内每个元素的后继元素,则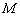 =
=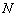 .
.
自然数就是满足上述公理的集合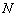 中的元素,关于自然数的所有性质都是这些公理的直接理论.由以上公理可知,0是自然数关于“后继”的起始元素,如果记0'= 1,1'= 2,2'= 3, …,
中的元素,关于自然数的所有性质都是这些公理的直接理论.由以上公理可知,0是自然数关于“后继”的起始元素,如果记0'= 1,1'= 2,2'= 3, …, '=
'= +1,…,则
+1,…,则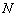 ={0,1,2…,
={0,1,2…, ,…}.
,…}.
由以上公理所定义的自然数与前面由集合所定义的自然数在本质上是一致的.20世纪90年代以前的中学数学教材将自然数的起始元素视作1,则自然数集即为正整数集.现在已统一采用上面的证法,即将0作为第1个自然数.
定理4(最小数原理)自然数集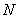 的任意非空子集
的任意非空子集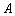 都有最小数.
都有最小数.
定理5 数学归纳原理—第Ⅰ型数学归纳法
一个与自然数相关的命题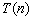 ,如果
,如果
(1) 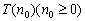 为真.
为真.
(2) 假设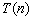
 为真,则可以推出
为真,则可以推出 也为真.
也为真.
那么,对所有大于、等于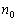 的自然数
的自然数 ,命题
,命题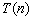 为真.
为真.
在具体运用数学归纳法进行数学证明时,有多种不同的形式,如下:
定理6 数学归纳法原理—第Ⅱ型数学归纳法
如果命题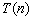 满足:
满足:
对某一个自然数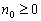 ,
,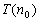 为真.
为真.
假设对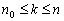 中的
中的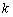 ,
,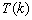 为真,则可以推出
为真,则可以推出 也为真.那么,对所有大于或等于
也为真.那么,对所有大于或等于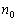 的自然数,命题
的自然数,命题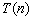 都为真.
都为真.
定理7 Ⅰ型与Ⅱ型数学归纳法等价.
证明:假设命题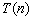 对(
对( =
=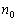 )为真,于是只需证明由“
)为真,于是只需证明由“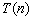
 为真,可以推出
为真,可以推出 也为真”的充要条件为“由
也为真”的充要条件为“由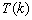
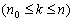 为真,可以推出
为真,可以推出 也为真.”
也为真.”
(1)充分性:
若“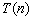 (
(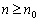 )为真,可以推出
)为真,可以推出 为真”,则对
为真”,则对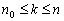 ,
,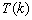 为真,特别
为真,特别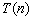 是为真,因此
是为真,因此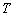 (
( +1)也为真.
+1)也为真.
(2)必要性: 反证法
若“由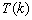
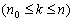 为真,可以推出
为真,可以推出 也为真”,但并非对所有大于或等于
也为真”,但并非对所有大于或等于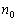 的自然数
的自然数 ,由
,由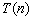 为真,可以推出
为真,可以推出 也为真,则
也为真,则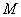 ={
={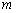 |
|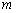 ∈
∈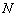 ,
,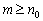 ,且由
,且由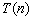 为真,推不出
为真,推不出 也为真}非空.由定理1,
也为真}非空.由定理1,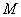 中有最小数
中有最小数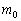 ,且对
,且对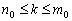 的
的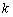 ,有
,有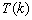 为真,可以推出
为真,可以推出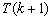 也为真,特别由
也为真,特别由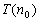 为真,可知
为真,可知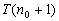 为真, 由
为真, 由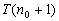 为真,可知
为真,可知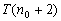 为真,……,由
为真,……,由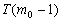 真,可知
真,可知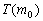 为真.现已知
为真.现已知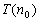 为真,所以
为真,所以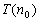 ,
,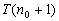 ……,
……,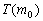 ,都为真.由此可知
,都为真.由此可知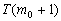 也为真,所以由
也为真,所以由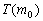 为真,推出了
为真,推出了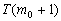 也为真,这与
也为真,这与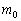 的选取矛盾.
的选取矛盾.
(三)、数学归纳法的步骤
数学归纳法的一般步骤如下:
验证 =1时命题成立.(此即归纳基础或递推基础)
=1时命题成立.(此即归纳基础或递推基础)
假设 =
=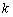 时命题成立.(此即归纳假设,或递推的根据)在这个假设下证明
时命题成立.(此即归纳假设,或递推的根据)在这个假设下证明 =
=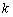 +1时命题成立.
+1时命题成立.
写一段“声明”,由于命题满足以上两个验算,根据数学归纳法原理,命题就对一切正整数 成立.
成立.
数学归纳法是一种论证方法,通常上用来证明数学上的猜想而这种猜想是用某种归纳法所获得的.
四、归纳法与数学归纳法的联系与区别
归纳法是发现规律的方法.但是由于归纳法得到的规律对某些题不一定正确,要判断所总结的规律(或结论)是否正确,要从理论上加以证明,这就要运用数学归纳法了.下述三道题足以说明两者的关系.
例3 已知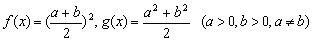 ,探求对于任意自然数
,探求对于任意自然数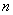 ,
,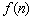 与
与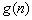 间的大小关系,并加以证明.
间的大小关系,并加以证明.
分析与解:本题比较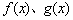 的大小,即
的大小,即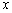 为变量,
为变量,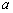 、
、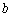 为常量.令
为常量.令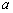 =3,
=3,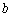 =1,则有
=1,则有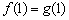 ,当
,当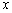 =2时,
=2时,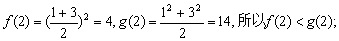
当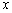 =3时,
=3时,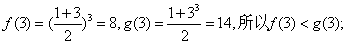
当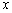 =4时,
=4时,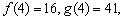
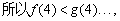
上述是用归纳法完成的.
可猜想对于任意自然数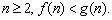
当 时,用数学归纳法证明于下:
时,用数学归纳法证明于下:
(1)当 =2时,
=2时,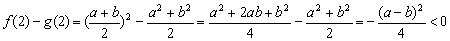
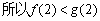 ,原不等式成立;
,原不等式成立;
(2)假设当 =
=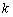 时,有
时,有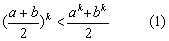
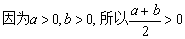 ,(1)式两边同乘以
,(1)式两边同乘以
则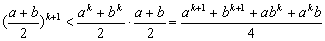
由于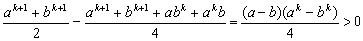 (
(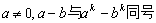 ),
),
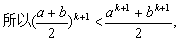 即当
即当 =
=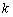 +1时,原不等式成立.
+1时,原不等式成立.
由(1)、(2)可知对于任意自然数 ,当
,当 时,不等式
时,不等式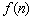 <
<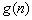 恒成立.
恒成立.
例4 由下列各不等式: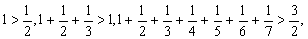
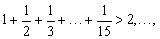 你能得到怎样的结论?并予以证明.
你能得到怎样的结论?并予以证明.
分析与解:从观察知,每一个不等式左边的第一项都是1,各项的分子都是1,且分母按自然数顺序排列.对这类命题一般规律探索的关键在于第 个不等式左端的首项及末项,以及不等式的右端.由四个不等式的右端:
个不等式左端的首项及末项,以及不等式的右端.由四个不等式的右端: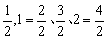 ,可知第
,可知第 个不等式右边为
个不等式右边为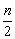 ;四个不等式左边最后一项的分母为:
;四个不等式左边最后一项的分母为:
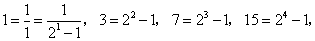 …,
…,
由此猜想第n项的分数的分母为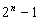 .这是采用归纳法得出的.
.这是采用归纳法得出的.
用数学归纳法证明如下:
① 当 =1时,猜想显然成立;
=1时,猜想显然成立;
② 假设 =
=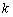 时,不等式成立,即
时,不等式成立,即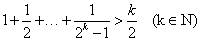 ,那么当
,那么当 =
=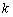 +1时,
+1时,
左边=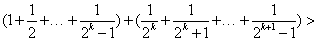
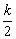 +
+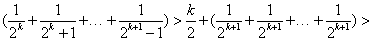
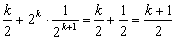 .
.

即当 =
=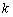 +1时,不等式成立.
+1时,不等式成立.
综合(1)、(2)知对一切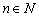 不等式成立.
不等式成立.
例5 数列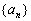 的各项均为正数,
的各项均为正数,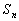 为前
为前 项和,如果
项和,如果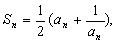
(1) 求 ;
;
(2) 归纳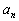 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
(1)解:由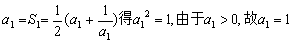 ;
;
由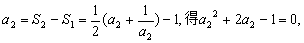 解之取正值得
解之取正值得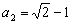 .
.
由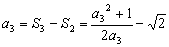 得:
得: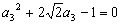
解之取正值得 ,猜想:
,猜想: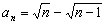 .
.
(2)证明:①当 =1时,命题成立;
=1时,命题成立;
②假设 =
=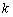 时,命题成立,即
时,命题成立,即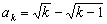 有
有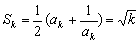 .
.
当 =
=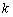 +1时,
+1时, ,得
,得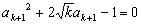 ,解之取正值
,解之取正值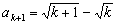 .命题对
.命题对 =
=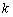 +1时成立.
+1时成立.
综合①、②对一切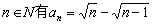 .
.
归纳法与数学归纳法使数学中发现规律论证关于自然数的命题是否正确的一种重要方法,它的特点是前者发现规律,后者予以理论上严谨的证明.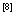
参考文献:
[1] [美]G.伯利亚.数学与猜想[M].数学名著译丛,1984.
[2] 郑仲义.学生对归纳和数学归纳法基础的理解[D].华东师范大学:硕士生毕业论文,2004.5.
[3] 张顺燕.数学的美与理[M].北京:高等教育出版社,2003.12:58-60.
[4] 陈石夫.归纳法在数学探索发现中的应用[J].福建中学数学,2002,10:11-13.
[5] 孙崇秀.数学归纳法刍议[J].数学教学研究,2000,5:30-31.
[6] 张艳丽.谈归纳原理和数学归纳法[J].衡水师专学报,2002.04:56-58.
[7] 刘云章,马复.数学直觉与发现[M].合肥:安徽教育出版社,1991.7.
[8] 杨玉声.归纳法与数学归纳法及其应用[J].中学理科,1999,Z2:15-17.
