这两周的微流控分析课程让共有五次课,时间虽短,却让我学到了很多。陈老师两周五次,每次4小时的辛勤付出,让我们接触了解一个年轻但非常具有活力的学科。然而,终究是要别离的,非常感谢陈老师的谆谆教诲。这是我的微流控分析课程总结,对陈老师上课的基本内容进行总结归纳,并且对微流控芯片的应用与发展进行了一定程度的研究。总结一共包括三个方面:微流控的间单介绍,微流控芯片的制作方法与驱动方式,微流控芯片的应用与展望。
一、什么是微流控
微流控通常被定义为在几微米至几百微米的通道内对小体积(10^-9~10^-18L)的液体样品进行处理或操作的一门系统科学和技术。微流控也称为微流控芯片(microfluidics)或芯片实验室(lab-on-a-chip,LOC),是指在一块几平方厘米的芯片上构建化学或生物实验室。它把化学和生物等领域中所涉及的样品制备、反应、分离、检测、细胞培养、分选、裂解等操作单元集成到一块芯片上,通过微通道形成网络,用可控流体贯穿整个系统,以实现常规化学或生物实验室的各种功能。
微流控芯片的基本特征和最大优势是多种单元技术在微小可控平台上的灵活组合和规模集成,可能会对人类未来的生活方式和生存质量产生影响,这种影响甚至可能是革命性的。
二、微流控芯片制作与驱动方法
微流控芯片制作涉及芯片材料的选择、加工、封接、表面处理以及与其他装置的集成等多个环节此就其主要技术进行简要介绍。
2. 1材料和制作方法
制作微流控芯片的材料多采用玻璃、硅或高分子聚合物。玻璃和硅具有良 好的化学、光学特性,使用光刻和蚀刻技术可实现高精度地复制二维或复杂的三维结构,但是其造价高,对制造加工环境的要求较高。高分子聚合物种类多,可通过软光刻技术或热塑技术加工,适于大批量一次性芯片的制作,并且物料成本相对较低,但是由于高分子聚合物的机械、化学特性不太稳定,需要适当地进行
表面修饰。现在多采用聚二甲基硅氧烷( PDMS) 制作芯片,PDMS 稳定、无毒,可塑性、透气性好,透明易于观察并具有很好的生物相容性。
芯片微通道的制作主要有如下方法:(1)光刻化学腐蚀方法;(2)等离子或反应离子深刻蚀方法,微通道的截面形状为矩形,可得到较高的深宽比;(3)注塑、印模或激光烧蚀;(4)软刻蚀技术(softlithography)等。键合是微流控芯片加工中一个关键的工艺环节,一般可分为直接键合、静电键合、热键合和粘接等方法,不同的材料,其制作方法也有所不同。
2. 2驱动方式方法及优缺点
微流控芯片的驱动方法包括(微量、精密)注射泵,电渗,电泳,重力,离心力和毛细作用。
注射泵的驱动可操作性强、流速范围广、重复性好,但它具有脉动、流阻大、对低流速要求高等缺点。电渗与电泳驱动的简单易操作、设备简单、体积小,但存在着产生焦耳热、电极附近发生电解反应产生气体、歧视效应、对表面要求高重复性差的缺点。重力驱动几乎不需要额外的设备,长期稳定,无脉动,但存在着可操作性差,对阻力变化敏感的缺点。离心力驱动同时驱动多组微通道,驱动的复杂度不受平行结构数目的影响、具有高通量,但具有与其他装置的连接、顺序操作较难、只能利用突破阀和转速等进行简单的控制的缺点。
三、应用与展望
微流控芯片技术具有重要的科研和经济价值。在医学上,流控芯片主要应用于遗传和单细胞分析、蛋白质研究、细胞迁移、药物筛选、干细胞和神经细胞培养等,加快医学研究的步伐;在农业上,可以对农作物进行病害、营养缺陷进行监测和检测,在病害未显症之前可以进行病害筛查,提前预防,减少病害发生和扩散,降低损失;在畜牧上可以进行药物输送,提高治疗效果,降低生产成本;在食品领域,对于食品中多样复杂的污染源,微流控技术可以充分发挥其快速、准确的优势,为食品安全提供技术支持。
微流控技术未来的发展必然是朝着微型化和集成化的方向进行。微流控芯片技术一开始就是以交叉学科的身份出现,因此决定了它可以与多种技术进行集成,发挥不同技术的优势以应对越来越多、越来越复杂的应用需求。另外,随着制造
和加工技术的不断进步,微通道尺寸将越来越小,结构将越来越复杂,在流体流动方向上通道的特征尺度将会常常跨越毫米、微米以及纳米量级。
目前,微流控芯片多处于研究阶段,其产品较少。同时,在实际生产生活中,对微流控芯片的使用率较低、缺乏统一标准等阻碍了微流控芯片市场的发展。将微流控芯片技术渗透到农业和食品行业需要工业制造方而的技术,解决在统一标准方面的漏洞;需要提高现有微流控的技术要求,改变其复杂性和价格昂贵性,使之成为一种功能性系统。虽然微流控技术在农业、食品领域的应用研究起步较晚,但其为提高农业和食品安全提供了新的途径,我们有理由相信它将大有可为。
第二篇:微积分课程总结
姓名:
学号:
微积分课程总结
第六章 定积分
6.2定义:

几点注意:
1、如果积分和式的极限存在,则此极限值是个常量;它与f(x)及积分区间[a,b]有关,而与积分变量用什么字母无关,即
2、无界函数是不可积的,即函数f(x)有界是可积的必要条件。
3、有限区间上的连续函数是可积的,有限区间上只有有限个间断点的有节函数也是可积的。
4、当 时,
时,
当 时,
时,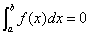
5、定积分的几何意义是曲边梯形的面积。
6.3定积分的基本性质:
性质1: (k为常数)
(k为常数)
性质2: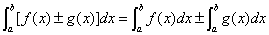 (此性质可以推广到任
(此性质可以推广到任
意有限多个代数和的情况)
性质3:积分的可加性——
无论c处去什么位置,该性质都成立。
性质4:如果函数f(x)与g(x)在区间[a,b]上总满足条件 ,
,
则
性质5:如果被积函数f(x)=1.则有
性质6:如果函数f(x)在区间[a,b]上的最大值与最小值分别为M
与m,则
性质7:(中值定理)如果函数f(x)在区间[a,b]上连续,则在[a,b]内至少又一点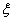 使得下式成立:
使得下式成立:

 #推论1:如果在区间[a,b]上,
#推论1:如果在区间[a,b]上, 则
则
#推论2:
6.4定积分与不定积分的关系:
定理6.1:如果函数f(x)在[a,b]上连续,则函数 对积分上限x的导数,等于被积函数在上限x处的值,即
对积分上限x的导数,等于被积函数在上限x处的值,即
定理6.2:(原函数存在定理)如果函数f(x)在区间[a,b]上连续,则函数
定理6.3:设函数f(x)在区间[a,b]上连续,且F(x)是f(x)的一个原函数,则 (注意:如果函数在所讨论的区间上不满足可积条件,则定理不能使用)
(注意:如果函数在所讨论的区间上不满足可积条件,则定理不能使用)
6.5定积分的换元积分法:
设函数f(x)在区间[a,b]上连续,令 ,如果
,如果
(1) 在区间[a,b]上又连续的导数
在区间[a,b]上又连续的导数 ;
;
(2)当t从 变到
变到 时
时 从
从 单调地变到
单调地变到 。则有
。则有 (定积分的换元公式)
(定积分的换元公式)
注意:在作变量替换时,要相应地替换积分上下限。
6.6定积分的分布积分法:
公式:
6.7定积分的应用:
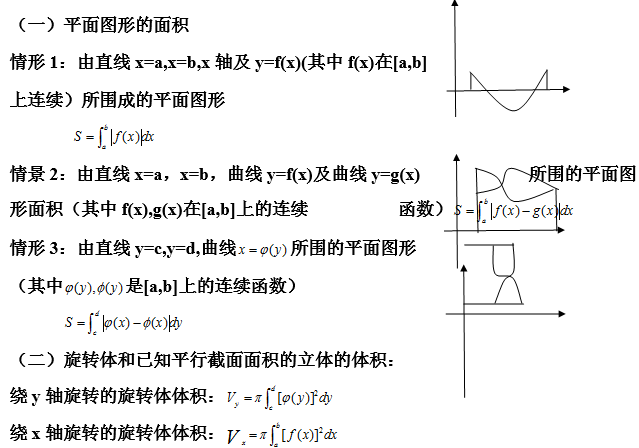
(三)经济应用问题:
例:由边际函数求总函数
已知总成本函数 ,总收益函数
,总收益函数 ,可知
,可知
边际成本函数 
边际收益函数 
则总成本函数为 
总收益函数为 
总利润函数为 
6.9广义积分
1、无限区间上的积分
设函数f(x)在区间 上连续,如果极限
上连续,如果极限 存在,就称此极限为为f(x)在
存在,就称此极限为为f(x)在 上的广义积分,记作
上的广义积分,记作

这是称广义积分 存在或收敛。如果
存在或收敛。如果 不存在,就说
不存在,就说 不存在或发散。
不存在或发散。
类似的有:
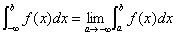

#对于广义积分 ,其收敛的充要条件是:
,其收敛的充要条件是:
 与
与 都收敛
都收敛
2、无界函数的积分
设函数f(x)在 上连续,当
上连续,当 时,
时, ,如果
,如果 存在,就称此极限值为
存在,就称此极限值为
无界函数f(x)在[a,b]上的广义积分,记作
这时称广义积分 存在或收敛。如果
存在或收敛。如果 不存在,就说
不存在,就说 不存在或发散。
不存在或发散。
类似情况:

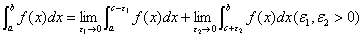
#对于 时
时 的广义积分
的广义积分 ,其存在的充要条件是:
,其存在的充要条件是:
 与
与
第七章 无穷级数
7.1概念
 如果当
如果当 时,部分和数列
时,部分和数列 的极限存在,即
的极限存在,即
(S是有限常数)则称级数收敛。如果 的极限不存在,则称级数发散。
的极限不存在,则称级数发散。
7.2无穷级数的基本性质:
定理7.1:如果级数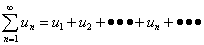
与级数 都收敛,他们的和
都收敛,他们的和
分别是S、W,则级数
 也收敛,且
也收敛,且
其和为
(注意:必须先说明 、
、 收敛,才能运用该性质)
收敛,才能运用该性质)
定理7.2:如果级数 收敛,且其和为S。
收敛,且其和为S。
则它的每一项都乘以一个不为零的常数a后,所
得到的的级数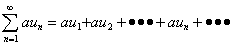 也收敛,
也收敛,
且其和为aS(即级数每一项同乘一个不为零的常
数后,其收敛性不变。
定理7.3:在一个级数的前面加上(或减去)有限项,级数
的敛散性不变。
定理7.4:如果一个级数收敛,加括号后所成的级数也收敛,
且与原级数有着相同的和。(反之,如果加括号后
所成的级数发散,则原级数也发散。另外,发散
级数加括号后有可能收敛,即加括号后级数收敛
原级数未必收敛。)
总结: 收敛级数
收敛级数 加括号
加括号 收敛级数
收敛级数
发散级数 去括号
去括号 发散级数
发散级数
收敛级数 去括号
去括号 级数不一定收敛
级数不一定收敛
发散级数 加括号
加括号 级数不一定发散
级数不一定发散
定理7.5:(收敛的必要条件)如果级数

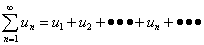 收敛,则
收敛,则 (即一般
(即一般
项极限为零,则级数发散;一般项极限不为零,则
不能判定极限的收敛性,选用其他方法)
7.3正项级数:
定理7.6:正项级数收敛的充要条件是:它的部分和数列
有界。
定理7.6:(比较判别法)如果两个正项级数

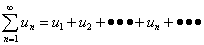 与
与
 满足关系式
满足关系式
 其中c是大于0的常数,那么:
其中c是大于0的常数,那么:
(1)当级数 收敛时,级数
收敛时,级数 也收敛
也收敛
(2)当级数 发散时,级数
发散时,级数 也发散
也发散
常用比较法级数总结:
(1)几何级数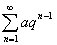 :当
:当 时收敛于
时收敛于 ,当
,当 时发散
时发散
(2)调和级数 发散
发散
(3) 级数
级数 :当
:当 时发散,当
时发散,当 是收敛
是收敛
定理7.8:(达朗贝尔比值法)如果正项级数
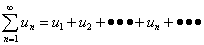

满足条件 ,则
,则
(1)当 时,级数收敛;
时,级数收敛;
(2)当 时,级数发散;
时,级数发散;
(3)当 时,不能用此法判定级数敛散性。
时,不能用此法判定级数敛散性。
总结:1、两个收敛级数相加得一收敛级数。
2、两个发散级数相加不一定是发散的。
3、一个收敛级数加上一个发散级数则为一发散级数。
7.4任意项级数、绝对收敛
定理7.9:(莱布尼茨定理)如果交错级数满足条件
(1) (2)
(2)
则级数收敛,其和
定理7.10:如果任意项级数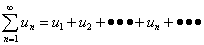 的各项绝 对值所组成的级数
的各项绝 对值所组成的级数
 收敛,则原级数也收敛。(注意:如果正项级数发散,则只能判断原级数非绝对收敛,而不能判断其为发散)
收敛,则原级数也收敛。(注意:如果正项级数发散,则只能判断原级数非绝对收敛,而不能判断其为发散)
定理7.11:如果任意项级数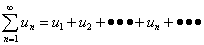 满足条件
满足条件 则当l<1是级数绝对收敛,当l>1是级数绝对发散。
则当l<1是级数绝对收敛,当l>1是级数绝对发散。
7.5幂级数
求幂级数收敛区间的步骤:先求出收敛半径R,如果0,则再判断 是的敛散性,最后写出收敛区间。
是的敛散性,最后写出收敛区间。
定理7.11:如果幂级数 的系数满足条件
的系数满足条件 则
则
(1)当 时,
时,
(2)当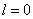 时,
时,
(3)当 时,
时,
注意:该定理只针对标准形式的幂级数。如果不是标准形式,可以考虑任意项收敛性判定公式。
(二)幂级数的性质
(1)如果幂级数 和
和 的收敛半径分别为
的收敛半径分别为 和
和 ,则
,则 的收敛半径等于
的收敛半径等于 和
和 中较小的那个。
中较小的那个。
(2)如果幂级数 的收敛半径
的收敛半径 ,则在收敛区间
,则在收敛区间 内,它的和级数
内,它的和级数 时连续级数。
时连续级数。
(3)幂级数可以在其收敛区间可以逐项积分,并且积分后级数的收敛半径也是R。
(4)幂级数可以在其收敛区间可以逐项微分,并且微分后级数的收敛半径也是R。
7.6泰勒级数和泰勒公式:
定理7.13(泰勒中值定理)如果函数 在含有点
在含有点 的区间
的区间 内,有一阶直到
内,有一阶直到 阶的连续导数,则当x取区间
阶的连续导数,则当x取区间 内任何值时,
内任何值时, 可以按
可以按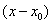 的方幂展开为
的方幂展开为
 其中
其中 (
(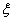 在
在 与
与 之间)则该公式称为函数f(x)的泰勒级数,余项称为拉格朗日型余项。
之间)则该公式称为函数f(x)的泰勒级数,余项称为拉格朗日型余项。
当令 时公式变为
时公式变为 再令
再令 ,
, 则
则 称为马克劳林公式。
称为马克劳林公式。
而 叫做泰勒级数,当
叫做泰勒级数,当 时,公式成为
时,公式成为 称为马克劳林级数。
称为马克劳林级数。
7.7某些初等级数的幂级数展开式:
(一)直接展开法:利用泰勒级数或马克劳林级数将f(x)展开为幂级数的步骤:1、求出f(x)在x=0的各阶导数值 ,若函数f(x)在x=0的某阶导数不存在,则f(x)不能展为幂级数 2、写出幂级数,并求出收敛区间
,若函数f(x)在x=0的某阶导数不存在,则f(x)不能展为幂级数 2、写出幂级数,并求出收敛区间
3、考察在收敛区间内余项 的极限
的极限 是否为0.如为0,则幂级数在此区间内等于函数f(x);如不为0,幂级数虽收敛,但它的和也不是f(x).
是否为0.如为0,则幂级数在此区间内等于函数f(x);如不为0,幂级数虽收敛,但它的和也不是f(x).
(二)间接展开法
总结:重要幂级数的展开式
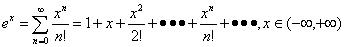






第八章 多元函数
8.1空间解析几何
空间任意两点之间的距离:
球面方程:
8.2多元函数
对于多元函数来说,可导不一定连续,连续同样不一定可导。
8.4偏导数
其多元函数对一自变量的偏导数时,只需将其他自变量看成常数,用一元函数求导法即可求得。


8.5全微分

必要条件:可微 偏导数存在,
偏导数存在,
 在
在 处连续(但偏导数不一定连续)
处连续(但偏导数不一定连续)
充分条件;存在连续偏导数 可微
可微
8.6复合函数微分法:


8.7隐含数的微分法;

8.8二元函数的极值
定理8.3:(极值存在的必要条件)如果函数f(x)在点 处有极值,且两个一阶偏导数存在,则有
处有极值,且两个一阶偏导数存在,则有 ,
,
定理8.4:(极限存在的充分条件)如果函数f(x)在点 的某一领域内有连续的二阶偏导数,且
的某一领域内有连续的二阶偏导数,且 时它的驻点设
时它的驻点设 则
则
(1)如果 ,且
,且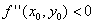 ,则
,则 是极大值
是极大值
(2)如果 ,且
,且 ,则
,则 是极小值
是极小值
(3)如果 ,则
,则 不是极值
不是极值
(4)如果 ,则
,则 是否为极值需另法判别
是否为极值需另法判别
*空间一点 到平面
到平面 的垂直距离公式:
的垂直距离公式:

8.9二重积分
性质1:常数因子可提到积分号外面
性质2:函数代数和的积分等于各个函数积分的代数和
性质3:二重积分的可加性
性质4:如果在区域D上总有 则,
则, 特别有
特别有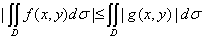
性质5:如果在区域D上有f(x,y)=1,A是D的面积,则
性质6:设M与m分别时函数z=f(x,y)在D上的最大值和最小值,A是D的面积,则
性质7:二重积分的中值定理:如果f(x,y)在闭区域D上连续,A是D的面积,则在D内至少存在一点 使得
使得 (中值定理的几何意义为:在区域D上以曲面f(x,y)为顶的曲顶柱体的体积,等于区域D上以某一点
(中值定理的几何意义为:在区域D上以曲面f(x,y)为顶的曲顶柱体的体积,等于区域D上以某一点 的函数值
的函数值 为高的平顶柱体的体积。
为高的平顶柱体的体积。
*二重积分的计算,可以归结为求两次定积分
(1)

(2)
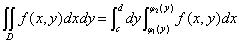
注意:如果平行与坐标轴的直线与区域D的边界线交点多于两点,则要将D分为几个小区域,使每个小区域的边界线与平行于坐标轴的直线的交点不多于两个。然后再应用积分对区域的可加性计算。
另外,计算二重积分时应先画出区域D的图形,再写出区域D上的点满足的不等式,从而确定积分上下限。
当区域D时圆或是圆的一部分,或者区域D的边界方程用极坐标表示较为简单,或者被积函数为 等形式时,一般采用极坐标计算二重积分。
等形式时,一般采用极坐标计算二重积分。
第九章 微分方程与差分方程
9.2一阶微分方程:
(1)可分离变量的一阶微分方程
形如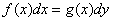
通解为
特别当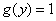 或
或 时得
时得 的通解为
的通解为
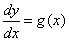 的通解为
的通解为
(2)齐次微分方程
形如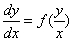
步骤:1、转换为标准形式
2、设 得
得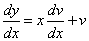 ,再将其代入可得到可分离变量的微分方程
,再将其代入可得到可分离变量的微分方程
则通解为 或
或
3,将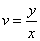 代入
代入
(3)一阶线性微分方程
形如
公式: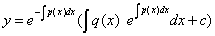
步骤:1、求对应的齐次方程的通解
2、设 ,并求出
,并求出
3、将第二步中的y及 代入,解出
代入,解出
4、将第三步求出的 代入第二步的y的表达式,得
代入第二步的y的表达式,得
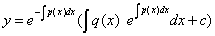
9.3几种二阶微分方程:
(1)最简单的二阶微分方程
形如 方法:对其积分一次得
方法:对其积分一次得 ,再对上式积分一次得
,再对上式积分一次得
(2)不显含未知函数y的二次微分方程
形如 令
令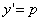 ,则
,则 代入方程得
代入方程得 求其通解为
求其通解为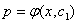 则方程的通解为
则方程的通解为
(3)不显含未知函数x的二次微分方程
形如 将其中的
将其中的 看作是y的函数
看作是y的函数 则
则 ,于是可将原方程化为
,于是可将原方程化为 ,设通解已求出为
,设通解已求出为 ,则由
,则由 可知原方程通解为
可知原方程通解为
9.4二阶常系数线性微分方程
一般形式:
将其转换成特征方程 求解,下面进行分类讨论
求解,下面进行分类讨论
(1)当 时,存在两个相异实根,且
时,存在两个相异实根,且
 ,
,  这时两个特解为
这时两个特解为
 和
和  所以通解为
所以通解为
(2)当 时,存在两个重根,且
时,存在两个重根,且 此时特解为
此时特解为
所以通解为
(3)当 时,存在两个共轭复根,且
时,存在两个共轭复根,且 ,
, 其中
其中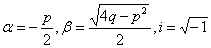 ,此时特解为
,此时特解为 ,
, ,则通解为
,则通解为
