首先说下我的感觉, 假如高等数学是棵树木得话,那么 极限就是他的根, 函数就是他的皮。树没有跟,活不下去,没有皮,只能枯萎, 可见这一章的重要性。
为什么第一章如此重要? 各个章节本质上都是极限, 是以函数的形式表现出来的,所以也具有函数的性质。函数的性质表现在各个方面
首先 对 极限的总结 如下
极限的保号性很重要 就是说在一定区间内 函数的正负与极限一致
1 极限分为 一般极限 , 还有个数列极限, (区别在于数列极限时发散的, 是一般极限的一种)
2解决极限的方法如下:(我能列出来的全部列出来了!!!!!你还能有补充么???)
1 等价无穷小的转化, (只能在乘除时候使用,但是不是说一定在加减时候不能用 但是前提是必须证明拆分后极限依然存在) e的X次方-1 或者 (1+x)的a次方-1等价于Ax 等等 。 全部熟记
(x趋近无穷的时候还原成无穷小)
2落笔他 法则 (大题目有时候会有暗示 要你使用这个方法)
首先他的使用有严格的使用前提!!!!!!
必须是 X趋近 而不是N趋近!!!!!!!(所以面对数列极限时候先要转化成求x趋近情况下的极限, 当然n趋近是x趋近的一种情况而已,是必要条件
(还有一点 数列极限的n当然是趋近于正无穷的 不可能是负无穷!)
必须是 函数的导数要存在!!!!!!!!(假如告诉你g(x), 没告诉你是否可导, 直接用无疑于找死!!)
必须是 0比0 无穷大比无穷大!!!!!!!!!
当然还要注意分母不能为0
落笔他 法则分为3中情况
1 0比0 无穷比无穷 时候 直接用
2 0乘以无穷 无穷减去无穷 ( 应为无穷大于无穷小成倒数的关系)所以 无穷大都写成了无穷小的倒数形式了。通项之后 这样就能变成1中的形式了
3 0的0次方 1的无穷次方 无穷的0次方
对于(指数幂数)方程 方法主要是取指数还取对数的方法, 这样就能把幂上的函数移下来了, 就是写成0与无穷的形式了 , ( 这就是为什么只有3种形式的原因, LNx两端都趋近于无穷时候他的幂移下来趋近于0 当他的幂移下来趋近于无穷的时候 LNX趋近于0)
3泰勒公式 (含有e的x次方的时候 ,尤其是含有正余旋 的加减的时候要 特变注意 !!!!)
E的x展开 sina 展开 cos 展开 ln1+x展开
对题目简化有很好帮助
4面对无穷大比上无穷大形式的解决办法
取大头原则 最大项除分子分母!!!!!!!!!!!
看上去复杂处理很简单 !!!!!!!!!!
5无穷小于有界函数的处理办法
面对复杂函数时候, 尤其是正余旋的复杂函数与其他函数相乘的时候,一定要注意这个方法。
面对非常复杂的函数 可能只需要知道它的范围结果就出来了!!!
6夹逼定理(主要对付的是数列极限!)
这个主要是看见极限中的函数是方程相除的形式 ,放缩和扩大。
7等比等差数列公式应用(对付数列极限) (q绝对值符号要小于1)
8各项的拆分相加 (来消掉中间的大多数) (对付的还是数列极限)
可以使用待定系数法来拆分化简函数
9求左右求极限的方式(对付数列极限) 例如知道Xn与Xn+1的关系, 已知Xn的极限存在的情况下, xn的极限与xn+1的极限时一样的 ,应为极限去掉有限项目极限值不变化
10 2 个重要极限的应用。 这两个很重要 !!!!!对第一个而言是X趋近0时候的sinx与x比值 。 地2个就如果x趋近无穷大 无穷小都有对有对应的形式
(地2个实际上是 用于 函数是1的无穷的形式 )(当底数是1 的时候要特别注意可能是用地2 个重要极限)
11 还有个方法 ,非常方便的方法
就是当趋近于无穷大时候
不同函数趋近于无穷的速度是不一样的!!!!!!!!!!!!!!!
x的x次方 快于 x! 快于 指数函数 快于 幂数函数 快于 对数函数 (画图也能看出速率的快慢) !!!!!!
当x趋近无穷的时候 他们的比值的极限一眼就能看出来了
12 换元法 是一种技巧,不会对模一道题目而言就只需要换元, 但是换元会夹杂其中
13假如要算的话 四则运算法则也算一种方法 ,当然也是夹杂其中的
14还有对付数列极限的一种方法,
就是当你面对题目实在是没有办法 走投无路的时候可以考虑 转化为定积分。 一般是从0到1的形式 。
15单调有界的性质
对付递推数列时候使用 证明单调性!!!!!!
16直接使用求导数的定义来求极限 ,
(一般都是x趋近于0时候,在分子上f(x加减麽个值)加减f(x)的形式, 看见了
有特别注意)
(当题目中告诉你F(0)=0时候 f(0)导数=0的时候 就是暗示你一定要用导数定义!!!!)
第二篇:高等数学中求极限的方法小结
宁波大红鹰学院学生数学课程论文
高等数学中求极限的方法小结
2.求极限的常用方法
2.1 利用等价无穷小求极限
这种方法的理论基础主要包括:(1)有限个无穷小的和、差、积仍是无穷小.(2)有界函数与无穷小的乘积是无穷小.(3)非零无穷小与无穷大互为倒数.(4)等价无穷小代换(当求两个无穷小之比的极限时,分子与分母都可用等价无穷小代替).
设?~??、?~??且lim[3]????lim;则:?与?是等价无穷小的充分必要条件为:??
????0(?).
常用等价无穷小:当变量x?0时,
sinx~x,tanx~x,arcsinx~x,arctanx~x,ex?1~x,ln(1?
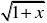
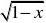
x)~x,1?cosx~12x,2~x,(1?x)??1~?x.
例1 求limx?01?cosx. xarctanx
解 ?x?0时,1?cosx~12x,arctanx~x, 2
12x1 故,原式?lim2? x?0x2
例2 求lim(1?x)?1. x?0cosx?1
1
23123解 ?x?0时,(1?x)?1~121x,1?cosx~x2,因此: 32
12x2??. 原式?limx?023x2
16
宁波大红鹰学院学生数学课程论文
例3 求
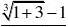
x?0. 1x11解 x?
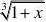
0时,1~x,tanx~x,故:原式=lim?. x?0x33
例4 求limx?0?ex?1?22xln(1?x).
解 x?0时,ex?1~x,ln(1?x)~x,故: x21原式?lim2?. x?02x2
例5 试确定常数a与n,使得当x?0时,ax与ln(1?x3)?x3为等价无穷小. n
?3x22?3x333ln(1?x)?x?3x5?1 而左边lim解 lim, ?limnn?1n?1x?0x?0x?0axnaxnax
?3?31?1??1?a??. 故 n?1?5即n?6 ?limx?06a6a2
2.2 利用洛必达法则求极限
利用这一法则的前提是:函数的导数要存在;为0比0型或者?型等未定式类型. ?
洛必达法则分为3种情况:(1)0比0,无穷比无穷的时候直接用.(2)0乘以无穷,无穷减去无穷(无穷大与无穷小成倒数关系时)通常无穷大都写成无穷小的倒数形式,通项之后,就能变成(1)中形式了.(3)0的0次方,1的无穷次方,无穷的0次方,对于(指数,幂函数)形式的方法主要是取指数的方法,这样就能把幂函数指数位置的函数移下来了,就是写成0与无穷的形式了.
洛必达法则中还有一个定理:当x?a时,函数f(x)及F(x)都趋于0;在点a的某去心邻域内,f(x)﹑F(x)的导数都存在且F(x)的导数不等于0;limx?af?(x)存在,那么F?(x)
limx?af(x)f?(x) [1]?lim . F(x)x?aF?(x)
17
宁波大红鹰学院学生数学课程论文
求极限有很多种方法如洛必达法则,夹逼定理求极限的秘诀是:强行代入,先定型后定法. [3]
1cos2x?). 例6 求lim(x?0sin2xx2
分析 秘诀强行代入,先定型后定法.
02?02(0?0)(0?0)0?00?0(此为强行代入以定型). ??32?2?4400000011
倘若不这样,或?0?0?可能是比?0?0?高阶的无穷小,(0?0)(0?0)0?00?0?2 或42000
(0?0)(0?0)0?00?0?. 43000
解
1cos2xx2?sin2xcos2x(x?sinxcosx)(x?sinxcosx)lim(2?2?lim?lim x?0sinxx?0x?0xx2sin2xx4
?limx?0x?sinxcosxx?sinxcosxx?sinxcosxlim?2lim, 33x?0x?0xxx
1?cos2x?sin2x4sin2x4?lim2?. 由洛必达法则的2,有:上式=2lim2x?03x3x?0x3
ex?1例7 求lim2. x?0x?x
(ex?1)?exex?1解 lim2?lim??1?lim2??1 . x?0(x?x)?x?02x?1x?0x?x
x3?3x?2例8 求lim3. x?1x?x2?x?1
3x2?36x3?lim?.(二次使用洛必达法则). 解 原式?lim2x?13x?2x?1x?16x?22
ex?e?x?2x例9 求lim. x?0x?sinx
18
宁波大红鹰学院学生数学课程论文
ex?e?x?2ex?e?xex?e?x
?lim?lim?2. 解 原式?limx?01?cosxx?0sinxx?0cosx
x2?4x?3例10 求lim2. x?1x?2x?1
2x?4x?2x?2?lim?lim?0?原式=?. x?12x?2x?1x?1x?1x?1
tanx?x例11 求lim. x?0xsinxarcsinx
112?1(1?cos)x22tanx?x1?cosx1解 原式?lim. ?lim?lim?lim?22222x?0x?0x?0x?0xxx3x3xcosx3xcosx3
cotx例12 求lim. x?0?lnx解 原式?lim
?sin2x?cos2x?1x?lim???. 解 原式?lim2?x?0?x?0sinx2sinxcosx
1cos2x?). 例13 求lim(x?0sin2xx2
x2?sin2xcos2x(x?sinxcosx)(x?sinxcosx)?lim解 原式?lim 224x?0x?0sinxxx
x?sinxcosxx?sinxcosxx?sinxcosx1?cos2x?sin2x4?limlim?2lim?2lim?x?0x?0x?0x?0x3xx33x23
“0??”型:
例14 求limx(x????2?arctanx).
?
解 原式?limx????arctanxx121?lim?lim?1. x???x????1x2x2
“???”型:
例15 求 lim?secx?tanx?.
x??
2
19
宁波大红鹰学院学生数学课程论文
解 ?secx?tanx?
故原式?lim
21sinx1?sinx??, cosxcosxcosx1?sinx?cosx?lim?0. ?cosx??sinxxx?2
“0”型:
xx例16 求lim. ?x?00
e解 原式?lim?x?0lnxx?lime?x?0xlnx?ex?0?limexlnx?1.
“1”型: ?
?e?例17 求lim?1??. x???x?
解 原式?lim?1?
“?”型: 0x?x???e??x?xee?ee.
(例18 求lim?x?01xtanx.
e解 原式?lim?x?0
x?01ln()tanxx?lime?x?0?tanxlnx?ex?0?lime?tanxlnx, (?tanxlnx)????lim?(?xlnx)?0,因此:原式=1. 而limtanx~x?x?0
2.3 泰勒公式
(含有e的x次方的时候,尤其是含有正、余弦的加减的时候要特别注意)
泰勒中值定理定理:如果函数f(x)在含有n的某个开区间(a,b)内具有直到(n?1) 阶的导数,则对任一?x?(a,b),有
f(n)(x0)f??(x0)2nf(x)?f(x0)+f?(x0)(x-x0)+(x-x0)+??+(x-x0)+Rn(x) n!2!
f(n?1)???n?1其中Rn(x)??x?x0?,这里?是x与x0之间的某个值. [1] n?1!
20
宁波大红鹰学院学生数学课程论文
例19 利用带有佩亚诺型余项的麦克劳林公式,求极限limsinx?xcosx. x?0sin3x
解 由于公式的分母sin3x~x3(x?0),我们只需将分子中的
x3x3
3sinx?x??0(x),xcosx?x??0(x3)代入计算, 3!2!
x3x313?0(x)?x??0(x3)?x3?0(x3),对上式做运算于是 sinx?xcosx?x?3!2!3
时,把两个x高阶的无穷小的代数和还是记作0(x). 33
14?33x?x?4例20 lim3?lim?3, 2x??x?2x?x?1x??1??2?3xxx
11?22n?1 lim?lim?1, 2x??(n?1)x??211??2nn323?
(?2)n?3n
limx??(?2)n??3n?1?2?????113?. ?lim??nx??32????2?????33??n
2.4 无穷小与有界函数的处理方法
面对复杂函数,尤其是正、余弦的复杂函数与其它函数相乘的时候,一定要注意这个方法.[3]
x?sinx. x??x
sinx1?lim(1?x)?1. 解 原式?lim(1?x??x??xx例21 求 lim
2.5 夹逼定理
主要介绍的是如何用之求数列极限,这个主要是看见极限中的通项是方式和的形式,对之放缩或扩大. [1]
21
宁波大红鹰学院学生数学课程论文
?2???sinsin?sin??例22 求lim???...??. n??n?1?n?n??2n??
i?i?i?sinsinsinnnn, 解 ?????1i?1n?oi?1n?1i?1n?i
sini?i?
n112lim??lim??sin?x?dx?, 0n??n??n?i?1n?oi?1nn
sini?
n?11ni??lim??? lim?n??n???n?1ni?1ni?1n?1
n12??1?sin?x?dx?, ??0??
根据夹逼定理 limx???i?1sini??2. 1?n?i
2.6 等比等差数列公式(?的绝对值要小于1) [1]
例23 设|?|?1,证等比数列1,?,???2n?1,?的极限为0.
n证 任取0???1,为使xn?a??,而xn?a??,使?n??,即
nln??ln?,n?ln?
ln?, 当N???ln???ln??ln?n?Nn?N?1?,当时,即, ????1?ln??ln???ln??
nnln??ln?????即xn?a??, 由定义知lim?n???1??0
???2?...?n...?lim????2?...?n??n???1?????1?.
因此,很显然有:
22
0.99...?lim0.99...?1. n??n?
2.7 各项以拆分相加[3]
将待求的和式子的各项拆分相加来消除中间的大多数,主要应用于数列极限,可以使用待定系数来拆分简化函数. 宁波大红鹰学院学生数学课程论文 ?
??111??...?例24 求lim?1???. n???2*33*4nn?1??
解 原式?lim?1??
n???111111?????...??? 2334nn?1?
11??? 2n?1? ?lim?1??
n???
1??3?lim??? n??2n?1??
=3. 2
2.8 求左右极限的方式
?x?1,x?0?例25 求函数f(x)??0,x?0,求x?0时,f?x?的极限.
?x?1,x?0?
f?x??lim解 lim?x?1???1,lim?f?x??lim??x?1??1, ??x?0x?0x?0x?0
f?x??limf?x?,所以,当x?0时,f(x)的极限不存在. 因为lim??x?0x?0
x?x例26 lim???0?. x?0x
x?(?x)x?x???lim(?x)?0lim?limx?0, 解 lim,???x?0x?0x?0?x?0xx
x?(?x)x?x?lim?0,所以,原式=0. 因为limx?0?x?0?xx
2.9 应用两个重要极限
23
宁波大红鹰学院学生数学课程论文
sinx?1?lim?1,lim?1???e x?0x??x?x?x
ex?1例27 求lim. x?0x
解 记x?ln?1?t? e?1?t,则 x
t?lim原式=limt?01?tt?01???1 ?因为lim?1?x?x?e?. 1x?????1?tln?1???t?1
1??例28 求lim?1??. n???n?1?n
1??解 原式=lim?1??n???n?1?
n?n?1??1=e. 1??例29 求lim?1??. n??n-1??
1??解 原式=lim?1??n???n-1??n?1??1=e.
n2.10 根据增长速度 lnx?x?e?x(x??)
xn
例30 求lim?x?n为正整数,??0?. x??e
n?n?1?xnxn?1
解 原式=lim?x=limx??ex???2e?x
例31 求limn?2?limn!?0. x???ne?xlnx?n?0?. x??xn
1lnx1解 limn?limn?1?limn?0. x??xx??nxx??nx
同函数趋近于无穷的速度是不一样的,x的x次方快于x!(x的阶乘)快于指数函数, 24
宁波大红鹰学院学生数学课程论文
快于幂函数,快于对数函数.
所以增长速度: lnx?xn?e?x(x??).
故以后上述结论可直接在极限计算中运用.
2.11 换元法
例32 lim(1?. x???1xx
解 令x??t,
1??1?e?t?1??1??则原式=lim?1???lim??lim1??1??????= t???t???t???ttt?1t?1????????
2.12 利用极限的运算法则[1]
利用如下的极限运算法则来求极限:
(1) 如果limf?x??A,limg?x??B,
那么lim[f(x)?g(x)]?limf(x)?limg(x)?A?B ?t?tt?1
lim??f?x??g?x????limf?x??limg?x??A?B
若又有B?0,则limf(x)limf(x)A?? g(x)limg(x)B
(2)如果limf(x)存在,而c为常数,则lim[cf(x)]?climf(x)
(3)如果limf(x)存在,而n为正整数,则lim[f(x)]n?[limf(x)]n
(4)如果?(x)??(x),而lim?(x)?a,lim?(x)?b,则a?b
(5)设有数列?xn?和?yn?,如果lim?xn?yn??A?B; n??
那么,lim?xn?yn??A?B;limxnyn?A?B n??n??
当yn?0?n?1,2,...?且b?0时,limn??xnA? ynB
2.13 求数列极限的时候可以将其转化为定积分[1]
25
宁波大红鹰学院学生数学课程论文
例33 已知f?
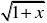
x?? ,在区间?0,1?上求lim
??0
?f????x(其中将?0,1?分为n
i
i
i?1
n
个小区间?xi?1,xi?,xi?1??i?xi,?为?xi中的最大值).
解 由已知得: lim
??0
?f??i??xi??f?x?dx
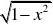
i?1
n
1
?
?
dx
?
?
4
.
(注释:由已知可以清楚的知道,该极限的求解可以转化为定积分,求函数f?x?在区间?0,1?上的面积).
在有的极限的计算中,需要利用到如下的一些结论、概念和方法:
(1)定积分中值定理:如果函数f?x?在积分区间?a,b?上连续,则在?a,b?上至少有一个点,使下列公式成立:
?f?x?dx???x??b?a? ?a???b?
a
b
;
(2)设函数f?x?在区间?a,???上连续,取t?a,如果极限 lim则称此极限为函数f?x?在无穷区间?a,???上的反常积分,记作
t???a
?f?x?dx存在,
t
?
??
f(x)dx,即
?
??
a
f(x)dx?lim?f(x)dx;
t???
a
t
设f?x?在区间?a,b?上连续且f?x??0,求以曲线y?f?x?为曲线,底为?a,b?的曲边梯形的面积A,把这个面积A表示为定积分:A=
?f?x?dx 的步骤是:
a
n
b
首先,用任意一组的点把区间?a,b?分成长度为?xi(i?1,2,...n)的n个小区间,相应地把曲线梯形分成n个窄曲边梯形,第i个窄曲边梯形的面积设为?Ai,于是有A?
其次,计算?Ai的近似值 ?Ai?f
??A;
i
i?1
??i??xi?xi?1??i?xi?;
26
宁波大红鹰学院学生数学课程论文
然后,求和,得A的近似值 A?
n
?f????x;
i
i
i?1
n
最后,求极限,得A?lim
??0
?f(?i)?xi??f(x)dx.
i?1
a
x0
2
x
b
?x?t?f?t?dt???.. 例34 设函数f?x?连续,且f?0??0,求极限 lim
x?f?x?t?dt
x?0
解 lim
x?0
?0?x?t?f?t?dt
x?f?x?t?dt
0x
x
=lim
x?0
?
x
xf?t?dt??tf?t?dt
x
x?f?u?du
x
,
f?t?dt+xf?x??xf?x??由洛必达得:lim
?f?u?du?xf?x?,
x?0
x0
x
?
其中f?x?t?dx,令u?x?t,得?f?u?du,
x
?
再由积分中值定理得:lim
x?0
xf???
?在0到x之间??xf??xfx?lim
x?0
f???f?0?1??
f??fxf0?f02
dx???1?x2.
??
.
例35 计算反常积分: 解
??
dx????
arctanxlimarctanx?limarctanx?(?)??. ===?????1?x2??x???x?-?22
2.14 利用函数有界原理证明极限的存在性,利用数列的逆推求极限
(1)单调有界数列必有极限;
(2)单调递增且有上界的数列必有极限,单调递减且有下界的数列必有极限. 例36 数列?xn?:2
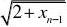
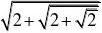
解 由已知可得?xn?单调递增且有界,由单调有界原理,知limxn 存在.
n??
[3]
27
宁波大红鹰学院学生数学课程论文
又xn?
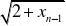
,limxn?

n??n记limxn=t,则t?n??
即可证xn?2,得到 t?2.
2.15 直接使用求导的定义求极限
当题目中告诉你F(0)?0时,F(x)的导数等于0的时候,就是暗示你一定要用导数定义:
(1)设函数y?f?x?在点x0的某个领域内有定义,当自变量x在x0处取得增量?x(点?x?x0仍在该领域内)时,相应的函数取得增量?y?f??x?x0??f?x0?;如果?y与?x之比?x?0时的极限存在,则称函数y?f?x?在点x0处可导,并称这个极限为函数y?f?x?在点x0处可导,并称这个极限为函数y?f?x?在点x0处的导数,记作f??x0?,即 f??x0??limf??x?x0??f?x0??y?lim; ?x?0?x?x?0?x
(2)在某点处可导的充分必要条件是左右导数都存在且相等.
例36 f?x???x?1??x?e??x???,求f
''???. 解 f??? =limx??f?x??f????lim?x?1??x?e???x?1??x?e?. x??x??
'例37 若函数f?x?有连续二阶导数且f?0?=0,f?0?=1,f''?0?=-2,
f?x??x??则 limx?0x2?.
A:不存在 B:0 C:-1 D:-2
f?x??xf'?x??11f'?x??f'?0?1''?f?0???1. ?lim?lim解 lim2x?0x?0x?02x2x2x?0
所以,答案为D.
28
宁波大红鹰学院学生数学课程论文
例38 若f(x)?x(x?1)(x?2)?.....(x?2010),求f?(0).
f(x)?f(0) x?0x
x(x?1)(x?2)?.....(x?2010) ?lim x?0x解 f?(0)?lim
?limx(x?1)(x?2)?.....(x?2010) x?0
?2010!.
2.16 利用连续性求极限[1]
例39 设f(x)在x?1处有连续的一阶导数,且f?(1)?
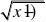
2,求lim?x?1d?(cosdx.
f?解
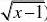
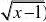

原式?lim?x?1?sin
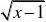
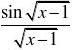
??1?limf2x?1?
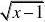
1??limf?
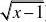
?x?12
1??f?(lim x?1?2
1??f?(1) 2
??1.
2.17 数列极限转为函数极限求解
数列极限中是n趋近,而不是x趋近.面对数列极限时,先要转化成求x趋近情况下的极限,当然n趋近是x趋近的一种情况而已,是必要条件.(还有数列极限的n当然是趋于正无穷的).
例40 求limn(1?nsin). n??2[1]1n
1sintt?sint1?cost1?lim?lim, ?t,则原式?lim2(1?32t?0t?0t?0ttt3tn
12t121所以在t?0时,1?cost与t等价,因此,原式?lim?. t?0226t3解 令
29
