北京邮电大学国际学院
高欢
Introduction to the Probability
1.1the fundamental knowledge about probability
Experiments : It is used in probability theory to describe virtually every progress whose outcome is not known in advance with certainty.
1. 
repeat again and again
2. Many outcomes
Experiments’ characteristic
3. Know all the outcomes, but do not know which one will be obtained in some experiment
4. Simple events , multiple events
the sample space: the collection of all possible outcomes of an experiment.
For example : roll a six-sided dice, the sample space contains the six numbers 1,2,3,4,5,6.
It can be written as
S={1,2,3,4,5,6}
1.2 the definition of Probability
In a given experiment, it is necessary to assign to each event A in the sample space S a number Pr(A) which indicates the probability that A will occur
1. For every event A, Pr(A)
0
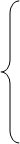
Axiom 2. Pr(S)=1
3. For every infinite sequence of disjoint events A1, A2, ……..
1. Pr(
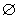)=0
2 . For every finite sequence of n disjoint events A1, …….,An,
Theorems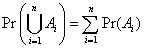 
3. For every event A, Pr(Ac)=1-Pr(A)
4. For every event A, 
5. For every two events A and B, Pr(A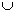
B)=Pr(A)+Pr(B)-Pr(AB)
Corollaries from the Axioms:
If A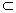
B, then Pr(BAc) = Pr(B) ? Pr(A)
If A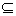
B, then Pr(A)
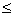Pr(B)
Example 1
Consider two events A and B such that Pr(A)=1/3 and Pr(B)=1/2. Determine the value of Pr(BAc) for each of the following conditions: (a) A and B are disjoint; (b) A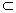B; (c) Pr(AB)=1/8
Solution:
(a) Pr(BAC)= 1/2 (b) Pr(BAC)= 1/2-1/3=1/6
(c) Pr(BAC)=Pr(B)-Pr(AB)=1/2-1/8=3/8
1.3 simple Sample Spaces and Combination Method
The definition of simple sample space:
A sample space S containing n outcomes s1, …….,sn is called a simple sample space if the probability assigned to each of the outcomes s1,…,sn is 1/n. If an event A in this simple sample space contains exactly m outcomes, then Pr(A)=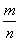
.
Example1:
Consider an experiment in which a fair coin is tossed once and a balanced die is rolled once.(a) Describe the sample space for this experiment. (b) What is the probability that a head will be obtained on the coin and an odd number will be obtained on the die?
Solution:
(a)
S={(head,1) (head, 2) (head,3) (head, 4) (head,5) (head, 6)
(tail, 1) (tail ,2) (tail, 3) (tail, 4) (tail, 5) (tail, 6)}
(b)
Pr(A)=
=1/4
Binomial cofficients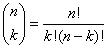 
For all numbers x and y and each positive integer n, (x+y)n =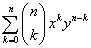 
Example 2
The United States Senate contains two senators from each of the 50 states.(a) If a committee of eight senators is selected at random, what is the probability that it will contain at least one of the two senators from a certain specified state?(b) what is the probability that a group of 50 senators selected at random will contain one senator from each state?
Solution: (a) Pr(A)=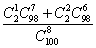
(b) Pr(B)=
1.4 The probability of a Union of Events
Theorem 1:
Pr(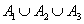
)= Pr(A1) +Pr(A2)+Pr(A3)-[Pr(A1A2)+Pr(A2A3)+Pr(A1A3)]+Pr(A1A2A3).
Example 1:
Suppose that four guests check their hats when they arrive at a restaurant, and that these hats are
returned to them in a random order when they leave. Determine the probability that no guests will receive the proper hat.
Solution: Pr(A)=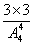
=
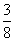
Example 2:
Among a group of 200 students, 137 students are enrolled in a mathematics class, 50 students are enrolled in a history class, and 124 students are enrolled in a music class. Furthermore, the number of students enrolled in both the math and history classes is 33, the number of students enrolled in both history and music classes is 29, the number of students enrolled in both math and music is 92. Finally the number of students enrolled in all three classes is 18. We shall determine the probability that a student selected at random from the group of 200 students will be enrolled in at least one of the three classes.
Solution :
let A denote the event that the selected student is enrolled in the math class. Let B denote the event that the selected student is enrolled in the history class. Let C denote the event that the selected student is enrolled in the music class.
Pr(A)=137/200 Pr(B)=50/200 Pr(C)=124//200
Pr(AB)=33/200 Pr(BC)=29/200 Pr(AC)=92/200
Pr(ABC)=18/200
We can get
Pr(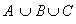
) =7/8
2 conditional probability
2.1 the definition of conditional probability
Pr(A|B)=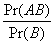
Pr(AB)=Pr(B)Pr(A|B) or Pr(AB)=Pr(A)Pr(B|A)
Suppose that A1,A2,….An are events such that Pr(A1A2..An-1)>0. Then
Pr(A1A2..An)=Pr(A1)Pr(A2|A1)Pr(A3|A1A2)…Pr(An|A1A2…An-1)
Suppose that A1,A2,…An, B are events such that Pr(A1A2..An-1|B)>0. Then
Pr(A1A2…An|B)=Pr(A1|B)Pr(A2|A1B)…Pr(An|A1A2..An-1B)
Example 1
Selecting four balls. Suppose that four balls are selected one at a time, without replacement, from a box containing r red balls and b blue balls(r>=2, b>=2). We shall determine the probability of obtaining the sequence of outcomes red, blue, red, blue.
Solution:
If we let Rj denote the event that a red ball is obtained on the jth draw and let Bj denote the event that a blue ball is obtained on the jth draw, then
Pr(R1B2R3B4)=Pr(R1)Pr(B2|R1)Pr(R3|R1B2)Pr(B4|R1B2R3)
=
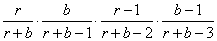
2.2 Independent Events
Definition: A and B are independent if and only if Pr(A|B)=Pr(A) and Pr(B|A)=Pr(B).
Pr(AB)=Pr(A)Pr(B)>=0
Theorem If two events A and B are independent, then the events A and BC are also independent Pr(ABC)=Pr(A)Pr(BC)
In particular, in order for three events A,B, and C to be independent, the following four relations must be satisfied:
Pr(AB)=Pr(A)Pr(B)
Pr(AC)=Pr(A)Pr(C)
Pr(BC)=Pr(B)Pr(C)
Pr(ABC)=Pr(A)Pr(B)Pr(C)
If A and B are independent event, then AC and BC are also independent
Proof: Pr(ACBC)=1-Pr(AB)
=1-Pr(A)-Pr(B)+Pr(A)Pr(B)
=[1-Pr(B)]-Pr(A)[1-Pr(B)]
=[1-Pr(B)][1-Pr(A)]=Pr(AC)Pr(BC)
Example 1
Two students A and B are both registered for a certain course. Assume that student A attends class 80 percent of the time, student B attends class 60 percent of the time, and the absences of two students are independent.
(a)what is the probability that at least one of the two students will be in class on a given day?
(b) if at least one of the two students is in class on a given day, what is the probability that A is in class that day.
Solution:
(a) Pr(A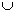B)=Pr(A)+Pr(B)-Pr(A
B)
=0.8+0.6-0.8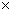
0.6
=0.92
(b)Pr(A|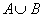
)=
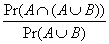=0.8/0.92=0.8696
Example 2
If A and B are independent events , Pr(A)=0.4, Pr(B)=0.7, what is the value of Pr(AC|BC)
Solution :
Pr(AC|BC)=Pr(AC)=1-Pr(A)=0.6
2.3 Bayes’ theorem
Theorem1 suppose that the events B1…Bk from a partition of the space S and Pr(Bj)>0 for j=1…k. Then , for every event A in S,
Pr(A)=
Theorem2 Bayes’ theorem. Let the event B1….,Bk from a partition of the space S such that Pr(Bj)>0 for j=1,….k, and let A be an event such that Pr(A)>0. Then , for i=1…,k,
Pr(Bi|A)=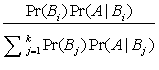
Example1
The percentages of voters classed as Liberals in three different election district are divided as follows: In the first district, 21 percent; in the second district, 45 percent; and in the third district, 75 percent. If a district is selected at random and a voter is selected at random from that district, what is the probability that she will be a Liberal?
Solution :
Pr(A)=
=0.47
Example 2
There is a sick tree, its host left the home to go on a journey. He ask his neighbor to water the tree. Suppose if the sick tree isn’t be watered, the probability of tree going dead is 0.8, if the tree is watered, the probability of going dead is 0.15. and we also know the probability that the neighbor remembers to water the tree is 0.9.
(a)when the host come back, what is the probability that the tree is still alive?
(b)when the host came back, he found the tree had been dead, what is the probability that the neighbor forgot to water the tree.
Solution:
(a)
Pr(A)=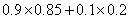
=0.785
(b) Pr(C1|B)=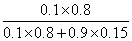
=0.372
3 Random Variables and Distribution
3.1 the additional konwledege about random variable
Definition of a random variable
Consider an experiment for which the sample space is denoted by S. A real-valued function that is defined on the space S is called a random variable. In other words, in a particular experiment a random variable X would be some function that assign a real number X(s) to each possible outcome s
S.
The uniform distribution on Integer/ discrete distribution
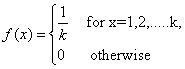
The uniform distribution on an interval/continuous distribution
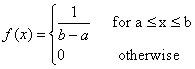
The binomial distribution
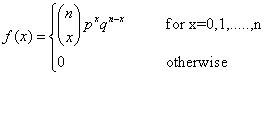
Poisson distribution
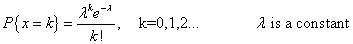
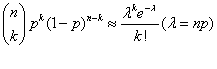
The distribution function
The distribution function F of a random variable X is a function defined for each real number x as follow: F(x)=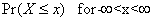
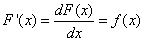
Uniform continuous distribution function
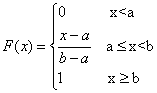
Exponential distribution and exponential distribution function
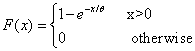
Normal distribution
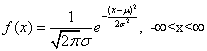
If X~N(μ，б2)， then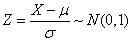 
3бtheory
Example 1
Suppose this the p.d.f. of a random variable X is as follows:
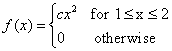
(a)Find the value of the constant c (b)Find the value of Pr(x>3/2)
(a)Solution:
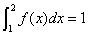
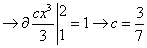
(b) Solution
Example2
Suppose that the d.f. of a random variable X is as follows
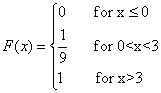
Find the p.d.f. of X
Solution:
3.2 Bivariate Distribution and Marginal Distribution
Discrete joint distribution f(x,y)= Pr(X=x and Y=y)
Continuous joint distribution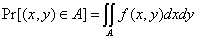 
Bivariate Distribution function F(x,y)=Pr(X<=x and Y<=y)
If the joint d.f . of two arbitrary random variable X and Y is F, then the probability that the pair (X,Y) will lie in a specified rectangle in the xy-plane can be found from F as follows: for example numbers a<b and c<d,
Pr(a<X<b and c<Y<d)=F(b,d)-F(a,d)-F(b,c)+F(a,c)
Marginal distribution
For the discrete distribution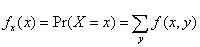 
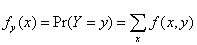
For the continuous joint distribution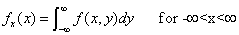 
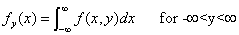
Note: X and Y will be independent if and only if f can be represented in the following form for 
: f(x,y)=g1(x)g2(x) where g1 is a nonnegative function of x alone and g2 is a nonnegative function of y alone.
Note: if X and Y are independent then h(x) and g(y) are independent
Example 1
Determining the joint p.d.f. from a Joint d.f. suppose that X and Y are random variables that can only take values in the intervals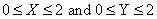 
. Suppose also that the joint d.f. of X and Y, for 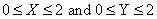, is as follows
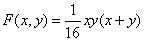
Solution:
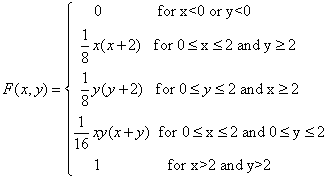
We can get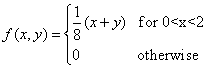
Example 2
Determining a Marginal p.f. and Marginal p.d.f. from a Joint p.d.f. suppose that the joint p.d.f. of X and Y is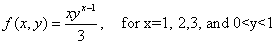 
determine the p.f of X and the marginal p.d.f. of Y
Solution:
The marginal p.f of X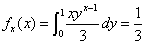 
For X=1,2,3. The marginal p.d.f. of Y is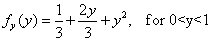 
Conditional distribution && the function of one or two random variables
conditional distribution
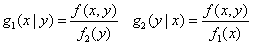
Function of a random variable
Suppose Y=r(X) g(y)=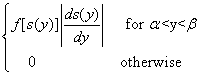
(Y must have inverse function)
Z=X+Y distribution
If X and Y are independent
This two formulas are also called convolution of p.d.f.’s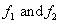 
.
M=max{X,Y} and N=min{X,Y} distribution
If X Y have the same d.f
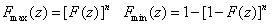
Example 1
Suppose that the p.d.f. of a random variable X is as follows:
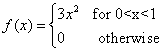also suppose that Y=1-X2. Determine the p.d.f. of Y.
Solution:
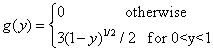
Example2
Suppose that X1 and X2 are i.i.d random variables and that each of them has a uniform distribution on the interval[0, 1]. Find the p.d.f. of Y=X1+X2
Solution:
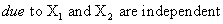
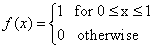
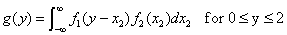
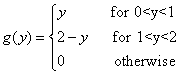
Example 3
Let X and Y be random variables for which the joint p.d.f. is as follow:
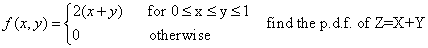
Solution:
Due to x y are not independent
