数列知识点总结
一、 数列的定义:(1)按一定次序排成的一列数
(2)数列可以看作是项数n的函数f(n)=an,其定义域为正整数集或它的子集。
二、数列的分类:
1、按项数分类:有穷数列
无穷数列
2、按增减性分类:递增数列——对于任何n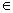 N+ ,具有
N+ ,具有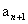 >
>
递减数列——对于任何n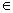 N+ ,具有
N+ ,具有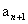 <
<
摆动数列
常数数列
3、按是否有界分类:有界数列——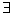 M
M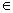 N+ ,使
N+ ,使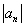
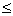 M
M
无界数列——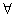
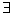 M
M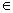 N+ ,总有
N+ ,总有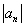
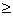 M
M
三、数列的表示法
1、解析法(公式法)通项公式或递推公式
2、列表法:
3、图象法:数列可用一群孤立的点表示
四、通项公式
五、数列的前n项和
六、递推公式
七、等差数列与等比数列
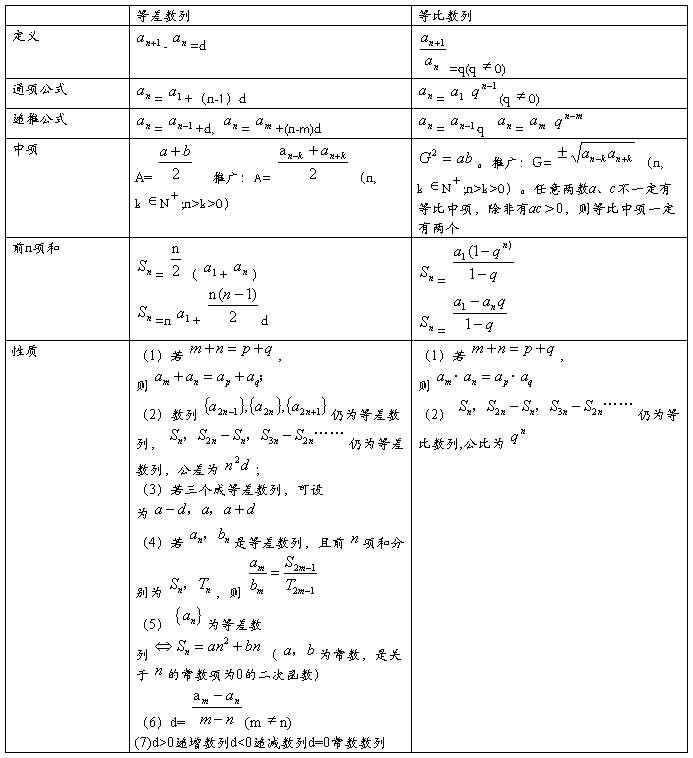
八、判断和证明数列是等差(等比)数列常有三种方法:
1、数列是不是等差数列有以下三种方法:
①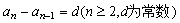
②2 (
( )
)
③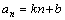 (
(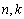 为常数).
为常数).
2、数列是不是等比数列有以下四种方法:
①
②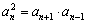 (
( ,
,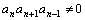 )①
)①
③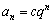 (
(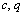 为非零常数).
为非零常数).
④正数列{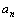 }成等比的充要条件是数列{
}成等比的充要条件是数列{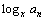 }(
}( )成等比数列.
)成等比数列.
九、求数列通项公式的方法
1、给出数列的前几项,求数列的一个通项公式——观察法。
例1、分别写出下面数列{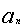 }的一个通项公式,使它的前4项分别是下列各数。
}的一个通项公式,使它的前4项分别是下列各数。
(1)1,3,5,7,…,
(2)1,2,1,2,…,
(3)2,22,222,2222,…,
2、通项公式法
3、涉及前n项和Sn求通项公式,利用an与Sn的基本关系式来求。即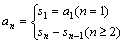
例2、在数列{an}中,Sn表示其前n项和,且Sn=n2,求通项an.
an=2n-1(n≥1).
例3、在数列{an}中,Sn表示其前n项和,且Sn=2-3an,求通项an.
4、已知递推公式(初始条件与递推关系),求通项公式。
(1)待定系数法。
若题目特征符合递推关系式a1=A,an+1=Ban+C(A,B,C均为常数,B≠1,C≠0)时,可用待定系数法构造等比数列求其通项公式。
例4、已知数列{an}满足a1=4,an=3an-1-2,求通项an.
(2)逐差相加法。
若题目特征符合递推关系式a1=A(A为常数),an+1=an+f(n)时,可用逐差相加法求数列的通项公式。
例5、在数列{an}中,a1=3,an+1=an+2n,求通项an.
(3)逐比连乘法。
若题目特征符合递推关系式a1=A(A为常数),an+1=f(n)·an时,可用逐比连乘法求数列的通项公式。
例6、在数列{an}中,a1=3,an+1=an·2n,求通项an.
(4)倒数法。
若题目特征符合递推关系式a1=A,Ban+Can+1+Dan·an+1=0
(A,B,C,D均为常数)时,可用倒数法求数列的通项公式。
例7、在数列{an}中,已知a1=1,an+1=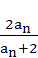 ,求数列的通项an.
,求数列的通项an.
(5)归纳法。
这是一种通过计算、观察、归纳规律,进而猜想、验证(证明)的思维方法,是一种普遍适用的方法。在前面所有的问题中,只要转化为递推公式,就可以由初始条件逐次代入递推关系,观察计算结果,直到看出规律为止。
例9、在数列{an}中,a1=3,an+1=an2,求数列的通项公式an.
十、求数列的前n项和的方法
1、、利用常用求和公式求和:利用下列常用求和公式求和是数列求和的最基本最重要的方法.
等差数列求和公式: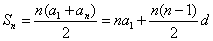
等比数列求和公式: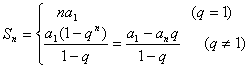
[例1] 已知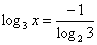 ,求
,求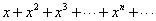 的前n项和.
的前n项和.
[例2] 设Sn=1+2+3+…+n,n∈N*,求 的最大值.
的最大值.
2、错位相减法求和:这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an· bn}的前n项和,其中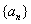 、
、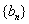 分别是等差数列和等比数列.
分别是等差数列和等比数列.
[例3]求和: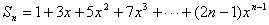 ………………………①
………………………①
[例4] 求数列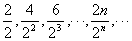 前n项的和.
前n项的和.
3、倒序相加法求和:这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到 个
个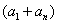 .
.
[例5] 求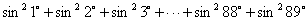 的值
的值
4、分组法求和:有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.
[例6] 求数列的前n项和: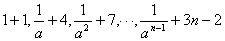 ,…
,…
[例7] 求数列{n(n+1)(2n+1)}的前n项和.
5、裂项法求和:这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)如:
(1) (2)
(2)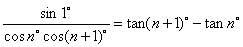
(3)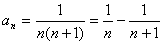 (4)
(4)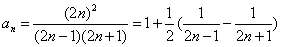
(5)
(6) 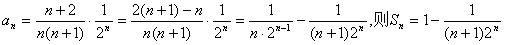
[例9] 求数列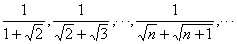 的前n项和.
的前n项和.
[例10] 在数列{an}中,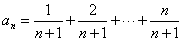 ,又
,又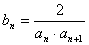 ,求数列{bn}的前n项的和.
,求数列{bn}的前n项的和.
[例11] 求证: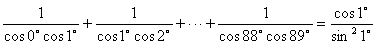
6、合并法求和:针对一些特殊的数列,将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和时,可将这些项放在一起先求和,然后再求Sn.
[例12] 求cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°的值.
[例13] 数列{an}: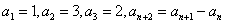 ,求S2002.
,求S2002.
[例14] 在各项均为正数的等比数列中,若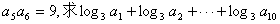 的值.
的值.
7、利用数列的通项求和:先根据数列的结构及特征进行分析,找出数列的通项及其特征,然后再利用数列的通项揭示的规律来求数列的前n项和,是一个重要的方法.
[例15] 求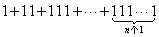 之和.
之和.
[例16] 已知数列{an}: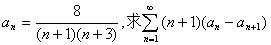 的值.
的值.
十一、在等差数列{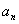 }中,有关Sn 的最值问题
}中,有关Sn 的最值问题
:(1)当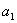 >0,d<0时,满足
>0,d<0时,满足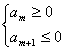 的项数m使得
的项数m使得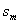 取最大值.
取最大值.
(2)当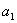 <0,d>0时,满足
<0,d>0时,满足 的项数m使得
的项数m使得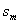 取最小值。在解含绝对值的数列最值问题时,注意转化思想的应用
取最小值。在解含绝对值的数列最值问题时,注意转化思想的应用
十二、 等比数列的前 项和公式的常见应用题:
项和公式的常见应用题:
⑴生产部门中有增长率的总产量问题. 例如,第一年产量为 ,年增长率为
,年增长率为 ,则每年的产量成等比数列,公比为
,则每年的产量成等比数列,公比为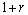 . 其中第
. 其中第 年产量为
年产量为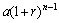 ,且过
,且过 年后总产量为:
年后总产量为:
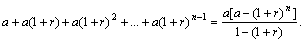
⑵银行部门中按复利计算问题. 例如:一年中每月初到银行存 元,利息为
元,利息为 ,每月利息按复利计算,则每月的
,每月利息按复利计算,则每月的 元过
元过 个月后便成为
个月后便成为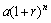 元. 因此,第二年年初可存款:
元. 因此,第二年年初可存款:
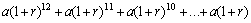 =
=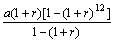 .
.
⑶分期付款应用题: 为分期付款方式贷款为a元;m为m个月将款全部付清;
为分期付款方式贷款为a元;m为m个月将款全部付清; 为年利率.
为年利率.
1. 已知等差数列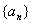 的前n项和为Sn,若
的前n项和为Sn,若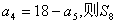 等于 ( D )
等于 ( D )
A.18 B.36 C.54 D.72
2. 已知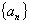 为等差数列,
为等差数列,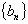 为等比数列,其公比
为等比数列,其公比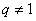 ,且
,且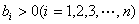 ,若
,若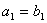 ,
,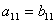 ,则 ( B )A.
,则 ( B )A.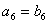 B.
B.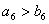 C.
C. D.
D.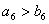 或
或
3. 在等差数列{a }中,3(a
}中,3(a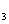 +a
+a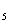 )+2(a
)+2(a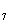 +a
+a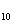 +a
+a )=24,则此数列的前13项之和为 ( D )
)=24,则此数列的前13项之和为 ( D )
A.156 B.13 C.12 D.26
4. 已知正项等比数列数列{an},bn=log a an, 则数列{bn}是 ( A )
A、等比数列 B、等差数列 C、既是等差数列又是等比数列 D、以上都不对
5. 数列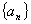 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且 是等比数列
是等比数列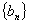 的相邻三项,若
的相邻三项,若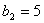 ,则
,则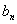 等于 ( B )
等于 ( B )
A. 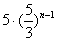 B.
B. 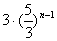 C.
C.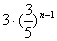 D.
D. 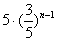
6. 数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…的第1000项的值是 ( B )
A. 42 B.45 C. 48 D. 51
7. 一懂n层大楼,各层均可召集n个人开会,现每层指定一人到第k层开会,为使n位开会人员上下楼梯所走路程总和最短,则k应取 ( D )A. n B.
n B. (n—1) C.
(n—1) C. (n+1)
(n+1)
D.n为奇数时,k= (n—1)或k=
(n—1)或k= (n+1),n为偶数时k=
(n+1),n为偶数时k= n
n
8. 设数列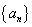 是等差数列,
是等差数列,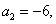
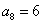 ,Sn是数列
,Sn是数列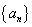 的前n项和,则( B )
的前n项和,则( B )
A.S4<S5 B.S4=S5 C.S6<S5 D.S6=S5
9. 等比数列 的首项
的首项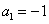 ,前
,前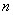 项和为
项和为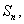 若
若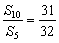 ,则公比
,则公比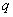 等于 ( B )
等于 ( B )
 C.2 D.-2
C.2 D.-2
10. 已知Sn是等差数列{an}的前n项和,若S6=36,Sn=324,Sn-6=144(n>6),则n等于 ( D )
A.15 B.16 C.17 D.18
11. 已知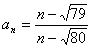 ,(
,( ),则在数列{
),则在数列{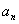 }的前50项中最小项和最大项分别是( C)
}的前50项中最小项和最大项分别是( C)
A.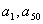 B.
B.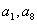 C.
C. 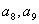 D.
D.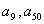
12. 已知: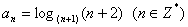 ,若称使乘积
,若称使乘积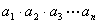 为整数的数n为劣数,则在区间(1,2002)内所有的劣数的和为 ( A )
为整数的数n为劣数,则在区间(1,2002)内所有的劣数的和为 ( A )
A.2026 B.2046 C.1024 D.1022
13. 在等差数列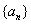 中,已知a1+a3+a5=18, an-4+an-2+an=108,Sn=420,则n= ___20___.
中,已知a1+a3+a5=18, an-4+an-2+an=108,Sn=420,则n= ___20___.
14. 在等差数列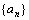 中,公差
中,公差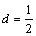 ,且
,且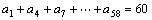 ,则
,则 (k∈N+,
(k∈N+,
k≤60)的值为 ________7________ .
15. 已知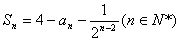 则 通项公式___
则 通项公式___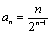 _________ .
_________ .
16. 已知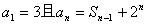 ,则
,则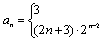
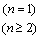 ;
; 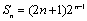
17. 若数列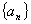 前n项和可表示为
前n项和可表示为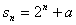 ,则
,则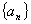 是否可能成为等比数列?若可能,求出a值;若不可能,说明理由.
是否可能成为等比数列?若可能,求出a值;若不可能,说明理由.
因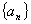 的前n 项和
的前n 项和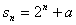 ,故
,故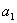 =
=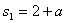 ,
,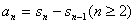 ,
,
an=2n+a-2n-1-a=2n-1(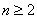 ).要使
).要使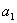 适合
适合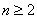 时通项公式,则必有
时通项公式,则必有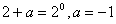 ,
,
此时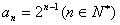 ,
, 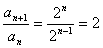 ,
,
故当a=-1时,数列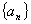 成等比数列,首项为1,公比为2,
成等比数列,首项为1,公比为2,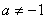 时,
时,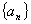 不是等比数列
不是等比数列
18.设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前n项和S10及T10.
【 解】 ∵{an}为等差数列,{bn}为等比数列,∴a2+a4=2a3,b2·b4=b32,
已知a2+a4=b3,b2·b4=a3,∴b3=2a3,a3=b32, 得b3=2b32,∵b3≠0,∴b3=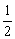 ,a3=
,a3=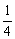 .
.
由a1=1,a3=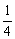 ,知{an}的公差d=-
,知{an}的公差d=-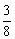 , ∴S10=10a1+
, ∴S10=10a1+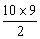 d=-
d=-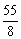 .
.
由b1=1,b3=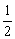 ,知{bn}的公比q=
,知{bn}的公比q=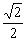 或q=-
或q=-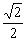 ,
,
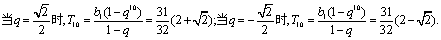
19.已知数列{an}是公比为q的等比数列,Sn是其前n项和,且S3,S9,S6成等差数列
(1)求证:a2 , a8, a5也成等差数列
【 解】 (1)S3=3a1, S9=9a1, S6=6a1, 而a1≠0,所以S3,S9,S6不可能成等差数列……2分
所以q≠1,则由公式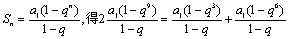
即2q6=1+q3 ∴2q6a1q=a1q+q3a1q , ∴2a8=a2+a5 所以a2, a8, a5成等差数列
(2)判断以a2, a8, a5为前三项的等差数列的第四项是否也是数列{an}中的一项,若是求出这一项,若不是请说明理由.
由2q6=1+q3=-
要以a2, a8, a5为前三项的等差数列的第四项是数列{an}中的第k项,
必有ak-a5=a8-a2,所以 所以
所以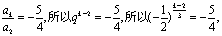
由k是整数,所以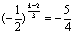 不可能成立,所以a2, a8, a5 为前三项的等差数列的第四项不可能也是数列{an}中的一项.
不可能成立,所以a2, a8, a5 为前三项的等差数列的第四项不可能也是数列{an}中的一项.
第二篇:高中数学必修5第二章《数列》精练检测题
高中数学必修5第二章《数列》精练检测题
一、选择题:
1.{an}是首项a1=1,公差为d=3的等差数列,如果an=2 005,则序号n等于( ).
A.667 B.668 C.669 D.670
2.在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=( ).
A.33 B.72 C.84 D.189
3.如果a1,a2,…,a8为各项都大于零的等差数列,公差d≠0,则( ).
A.a1a8>a4a5 B.a1a8<a4a5 C.a1+a8<a4+a5 D.a1a8=a4a5
4.已知方程(x2-2x+m)(x2-2x+n)=0的四个根组成一个首项为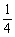 的等差数列,则
的等差数列,则
|m-n|等于( ).
A.1 B. C.
C.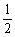 D.
D. 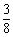
5.等比数列{an}中,a2=9,a5=243,则{an}的前4项和为( ).
A.81 B.120 C.168 D.192
6.若数列{an}是等差数列,首项a1>0,a2 003+a2 004>0,a2 003·a2 004<0,则使前n项和Sn>0成立的最大自然数n是( ).
A.4 005 B.4 006 C.4 007 D.4 008
7.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列, 则a2=( ).
A.-4 B.-6 C.-8 D. -10
8.设Sn是等差数列{an}的前n项和,若 =
=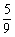 ,则
,则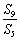 =( ).
=( ).
A.1 B.-1 C.2 D.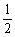
9.已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,则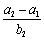 的值是( ).
的值是( ).
A.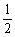 B.-
B.-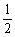 C.-
C.-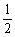 或
或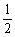 D.
D.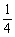
10.在等差数列{an}中,an≠0,an-1-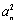 +an+1=0(n≥2),若S2n-1=38,则n=( ).
+an+1=0(n≥2),若S2n-1=38,则n=( ).
A.38 B.20 C.10 D.9
二、填空题
11.设f(x)= ,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值为 .
,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值为 .
12.已知等比数列{an}中,
(1)若a3·a4·a5=8,则a2·a3·a4·a5·a6= .
(2)若a1+a2=324,a3+a4=36,则a5+a6= .
(3)若S4=2,S8=6,则a17+a18+a19+a20= .
13.在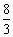 和
和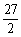 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .
14.在等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项之和为 .
15.在等差数列{an}中,a5=3,a6=-2,则a4+a5+…+a10= .
16.设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,则f(4)= ;当n>4时,f(n)= .
三、解答题
17.(1)已知数列{an}的前n项和Sn=3n2-2n,求证数列{an}成等差数列.
(2)已知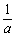 ,
,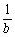 ,
,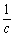 成等差数列,求证
成等差数列,求证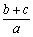 ,
,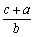 ,
, 也成等差数列.
也成等差数列.
18.设{an}是公比为 q 的等比数列,且a1,a3,a2成等差数列.
(1)求q的值;
(2)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
19.数列{an}的前n项和记为Sn,已知a1=1,an+1=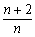 Sn(n=1,2,3…).
Sn(n=1,2,3…).
求证:数列{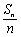 }是等比数列.
}是等比数列.
20.已知数列{an}是首项为a且公比不等于1的等比数列,Sn为其前n项和,a1,2a7,3a4成等差数列,求证:12S3,S6,S12-S6成等比数列.
第二章 数列
参考答案
一、选择题
1.C
解析:由题设,代入通项公式an=a1+(n-1)d,即2 005=1+3(n-1),∴n=699.
2.C
解析:本题考查等比数列的相关概念,及其有关计算能力.
设等比数列{an}的公比为q(q>0),由题意得a1+a2+a3=21,
即a1(1+q+q2)=21,又a1=3,∴1+q+q2=7.
解得q=2或q=-3(不合题意,舍去),
∴a3+a4+a5=a1q2(1+q+q2)=3×22×7=84.
3.B.
解析:由a1+a8=a4+a5,∴排除C.
又a1·a8=a1(a1+7d)=a12+7a1d,
∴a4·a5=(a1+3d)(a1+4d)=a12+7a1d +12d2>a1·a8.
4.C
解析:
解法1:设a1=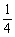 ,a2=
,a2=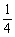 +d,a3=
+d,a3=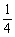 +2d,a4=
+2d,a4=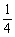 +3d,而方程x2-2x+m=0中两根之和为2,x2-2x+n=0中两根之和也为2,
+3d,而方程x2-2x+m=0中两根之和为2,x2-2x+n=0中两根之和也为2,
∴a1+a2+a3+a4=1+6d=4,
∴d=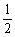 ,a1=
,a1=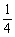 ,a4=
,a4= 是一个方程的两个根,a1=
是一个方程的两个根,a1= ,a3=
,a3=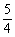 是另一个方程的两个根.
是另一个方程的两个根.
∴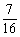 ,
,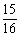 分别为m或n,
分别为m或n,
∴|m-n|=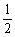 ,故选C.
,故选C.
解法2:设方程的四个根为x1,x2,x3,x4,且x1+x2=x3+x4=2,x1·x2=m,x3·x4=n.
由等差数列的性质:若g+s=p+q,则ag+as=ap+aq,若设x1为第一项,x2必为第四项,则x2= ,于是可得等差数列为
,于是可得等差数列为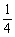 ,
, ,
,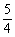 ,
, ,
,
∴m=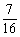 ,n=
,n=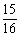 ,
,
∴|m-n|=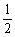 .
.
5.B
解析:∵a2=9,a5=243, =q3=
=q3=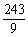 =27,
=27,
∴q=3,a1q=9,a1=3,
∴S4=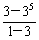 =
=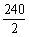 =120.
=120.
6.B
解析:
解法1:由a2 003+a2 004>0,a2 003·a2 004<0,知a2 003和a2 004两项中有一正数一负数,又a1>0,则公差为负数,否则各项总为正数,故a2 003>a2 004,即a2 003>0,a2 004<0.
∴S4 006=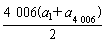 =
= >0,
>0,
∴S4 007=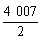 ·(a1+a4 007)=
·(a1+a4 007)=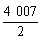 ·2a2 004<0,
·2a2 004<0,
故4 006为Sn>0的最大自然数. 选B.
 解法2:由a1>0,a2 003+a2 004>0,a2 003·a2 004<0,同解法1的分析得a2 003>0,a2 004<0,
解法2:由a1>0,a2 003+a2 004>0,a2 003·a2 004<0,同解法1的分析得a2 003>0,a2 004<0,
∴S2 003为Sn中的最大值.
∵Sn是关于n的二次函数,如草图所示,
∴2 003到对称轴的距离比2 004到对称轴的距离小,
∴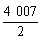 在对称轴的右侧.
在对称轴的右侧.
根据已知条件及图象的对称性可得4 006在图象中右侧零点B的左侧,4 007,4 008都在其右侧,Sn>0的最大自然数是4 006.
7.B
解析:∵{an}是等差数列,∴a3=a1+4,a4=a1+6,
又由a1,a3,a4成等比数列,
∴(a1+4)2=a1(a1+6),解得a1=-8,
∴a2=-8+2=-6.
8.A
解析:∵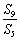 =
=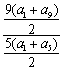 =
=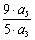 =
=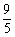 ·
·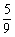 =1,∴选A.
=1,∴选A.
9.A
解析:设d和q分别为公差和公比,则-4=-1+3d且-4=(-1)q4,
∴d=-1,q2=2,
∴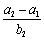 =
=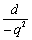 =
=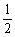 .
.
10.C
解析:∵{an}为等差数列,∴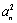 =an-1+an+1,∴
=an-1+an+1,∴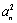 =2an,
=2an,
又an≠0,∴an=2,{an}为常数数列,
而an=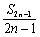 ,即2n-1=
,即2n-1=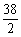 =19,
=19,
∴n=10.
二、填空题
11.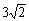 .
.
解析:∵f(x)=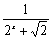 ,
,
∴f(1-x)=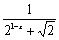 =
=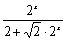 =
=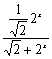 ,
,
∴f(x)+f(1-x)=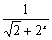 +
+ =
=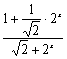 =
=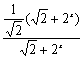 =
=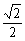 .
.
设S=f(-5)+f(-4)+…+f(0)+…+f(5)+f(6),
则S=f(6)+f(5)+…+f(0)+…+f(-4)+f(-5),
∴2S=[f(6)+f(-5)]+[f(5)+f(-4)]+…+[f(-5)+f(6)]=6 ,
,
∴S=f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)=3 .
.
12.(1)32;(2)4;(3)32.
解析:(1)由a3·a5=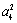 ,得a4=2,
,得a4=2,
∴a2·a3·a4·a5·a6=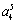 =32.
=32.
(2)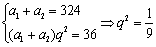 ,
,
∴a5+a6=(a1+a2)q4=4.
(3) ,
,
∴a17+a18+a19+a20=S4q16=32.
13.216.
解析:本题考查等比数列的性质及计算,由插入三个数后成等比数列,因而中间数必与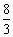 ,
,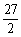 同号,由等比中项的中间数为
同号,由等比中项的中间数为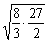 =6,
=6, 插入的三个数之积为
插入的三个数之积为 ×
×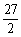 ×6=216.
×6=216.
14.26.
解析:∵a3+a5=2a4,a7+a13=2a10,
∴6(a4+a10)=24,a4+a10=4,
∴S13=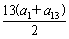 =
=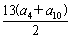 =
=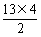 =26.
=26.
15.-49.
解析:∵d=a6-a5=-5,
∴a4+a5+…+a10
=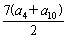
=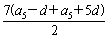
=7(a5+2d)
=-49.
16.5,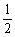 (n+1)(n-2).
(n+1)(n-2).
解析:同一平面内两条直线若不平行则一定相交,故每增加一条直线一定与前面已有的每条直线都相交,∴f(k)=f(k-1)+(k-1).
由f(3)=2,
f(4)=f(3)+3=2+3=5,
f(5)=f(4)+4=2+3+4=9,
……
f(n)=f(n-1)+(n-1),
相加得f(n)=2+3+4+…+(n-1)=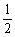 (n+1)(n-2).
(n+1)(n-2).
三、解答题
17.分析:判定给定数列是否为等差数列关键看是否满足从第2项开始每项与其前一项差为常数.
证明:(1)n=1时,a1=S1=3-2=1,
当n≥2时,an=Sn-Sn-1=3n2-2n-[3(n-1)2-2(n-1)]=6n-5,
n=1时,亦满足,∴an=6n-5(n∈N*).
首项a1=1,an-an-1=6n-5-[6(n-1)-5]=6(常数)(n∈N*),
∴数列{an}成等差数列且a1=1,公差为6.
(2)∵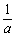 ,
,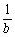 ,
,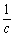 成等差数列,
成等差数列,
∴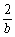 =
=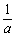 +
+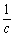 化简得2ac=b(a+c).
化简得2ac=b(a+c).
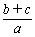 +
+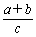 =
=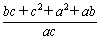 =
=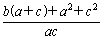 =
=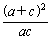 =
= =2·
=2·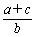 ,
,
∴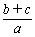 ,
,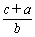 ,
,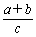 也成等差数列.
也成等差数列.
18.解:(1)由题设2a3=a1+a2,即2a1q2=a1+a1q,
∵a1≠0,∴2q2-q-1=0,
∴q=1或-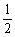 .
.
(2)若q=1,则Sn=2n+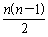 =
=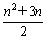 .
.
当n≥2时,Sn-bn=Sn-1=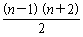 >0,故Sn>bn.
>0,故Sn>bn.
若q=-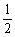 ,则Sn=2n+
,则Sn=2n+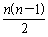 (-
(-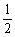 )=
)= .
.
当n≥2时,Sn-bn=Sn-1=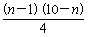 ,
,
故对于n∈N+,当2≤n≤9时,Sn>bn;当n=10时,Sn=bn;当n≥11时,Sn<bn.
19.证明:∵an+1=Sn+1-Sn,an+1=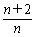 Sn,
Sn,
∴(n+2)Sn=n(Sn+1-Sn),整理得nSn+1=2(n+1) Sn,
所以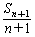 =
=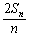 .
.
故{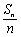 }是以2为公比的等比数列.
}是以2为公比的等比数列.
20.证明:由a1,2a7,3a4成等差数列,得4a7=a1+3a4,即4 a1q6=a1+3a1q3,
变形得(4q3+1)(q3-1)=0,
∴q3=-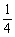 或q3=1(舍).
或q3=1(舍).
由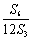 =
= =
=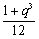 =
=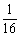 ;
;
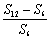 =
=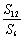 -1=
-1= -1=1+q6-1=
-1=1+q6-1=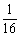 ;
;
得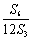 =
=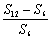 .
.
∴12S3,S6,S12-S6成等比数列.
