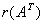总结求矩阵的逆矩阵的方法
课 程 名 称:
专 业 班 级:
成 员 组 成:
联 系 方 式:
摘要:矩阵是线性代数的主要内容,很多实际问题用矩阵的思想去解既简单又快捷.逆矩阵又是矩阵理论的很重要的内容, 逆矩阵的求法自然也就成为线性代数
研究的主要内容之一.本文将给出几种求逆矩阵的方法.
关键词:矩阵逆矩阵方法
Method of finding inverse matrix
Abstract:
Matrix in linear algebra is the main content,many prictical problems with the matrix theory is simple and fast. The inverse matrix andmatrix theory the important content, the solution of inverse matrix nature has become one of the main research contents of linear algebra. The paper will give some method of finding inverse matrix.
Key words:
Matrix inversematrix method
正文:
1.引言:矩阵是线性代数的主要内容,很多实际问题用矩阵的思想去解既简单又快捷.逆矩阵又是矩阵理论的很重要的内容, 逆矩阵的求法自然也就成为线性代
数研究的主要内容之一.本文将给出几种求逆矩阵的方法.
2.求矩阵的逆矩阵的方法总结:
2.1
矩阵的基本概念
矩阵,是由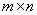 个数组成的一个
个数组成的一个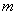 行
行 列的矩形表格,通常用大写字母
列的矩形表格,通常用大写字母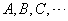 表示,组成矩阵的每一个数,均称为矩阵的元素,通常用小写字母其元素
表示,组成矩阵的每一个数,均称为矩阵的元素,通常用小写字母其元素 表示,其中下标
表示,其中下标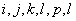 都是正整数,他们表示该元素在矩阵中的位置。比如,
都是正整数,他们表示该元素在矩阵中的位置。比如, 或
或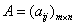 表示一个
表示一个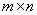 矩阵,下标
矩阵,下标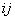 表示元素
表示元素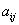 位于该矩阵的第
位于该矩阵的第 行、第
行、第 列。元素全为零的矩阵称为零矩阵。
列。元素全为零的矩阵称为零矩阵。
特别地,一个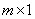 矩阵
矩阵 ,也称为一个
,也称为一个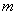 维列向量;而一个
维列向量;而一个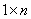 矩阵 ,也称为一个
矩阵 ,也称为一个 维行向量。
维行向量。
当一个矩阵的行数 与烈数
与烈数 相等时,该矩阵称为一个
相等时,该矩阵称为一个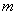 阶方阵。对于方阵,从左上角到右下角的连线,称为主对角线;而从左下角到右上角的连线称为付对角线。若一个
阶方阵。对于方阵,从左上角到右下角的连线,称为主对角线;而从左下角到右上角的连线称为付对角线。若一个 阶方阵的主对角线上的元素都是
阶方阵的主对角线上的元素都是 ,而其余元素都是零,则称为单位矩阵,记为
,而其余元素都是零,则称为单位矩阵,记为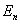 ,即:
,即: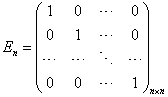 。如一个
。如一个 阶方阵的主对角线上(下)方的元素都是零,则称为下(上)三角矩阵,例如,
阶方阵的主对角线上(下)方的元素都是零,则称为下(上)三角矩阵,例如,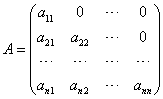 是一个
是一个 阶下三角矩阵,而
阶下三角矩阵,而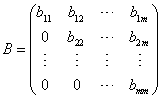 则是一个
则是一个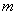 阶上三角矩阵。今后我们用
阶上三角矩阵。今后我们用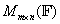 表示数域
表示数域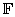 上的
上的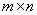 矩阵构成的集合,用
矩阵构成的集合,用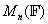 表示数域
表示数域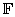 上的
上的 阶方阵构成的集合。
阶方阵构成的集合。
2.2求逆矩阵的方法:
1.利用定义求逆矩阵
定义: 设A、B 都是n 阶方阵, 如果存在n 阶方阵B 使得AB= BA = E, 则称A为可逆矩阵, 而称B为A 的逆矩阵.下面举例说明这种方法的应用.
例1 求证: 如果方阵A 满足A k= 0, 那么EA是可逆矩阵, 且
(E-A) = E + A + A
= E + A + A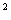 +…+A
+…+A
证明 因为E 与A 可以交换, 所以
(E- A )(E+A + A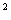 +…+ A
+…+ A )= E-A
)= E-A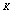 ,
,
因A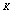 = 0 ,于是得
= 0 ,于是得
(E-A)(E+A+A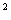 +…+A
+…+A )=E,
)=E,
同理可得(E + A + A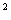 +…+A
+…+A )(E-A)=E,
)(E-A)=E,
因此E-A是可逆矩阵,且
(E-A) = E + A + A
= E + A + A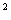 +…+A
+…+A .
.
同理可以证明(E+ A)也可逆,且
(E+ A) = E -A + A
= E -A + A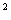 +…+(-1)
+…+(-1) A
A .
.
由此可知, 只要满足A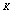 =0,就可以利用此题求出一类矩阵E
=0,就可以利用此题求出一类矩阵E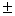 A的逆矩阵.
A的逆矩阵.
例2 设 A =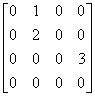 ,求 E-A的逆矩阵.
,求 E-A的逆矩阵.
分析 由于A中有许多元素为零, 考虑A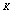 是否为零矩阵, 若为零矩阵, 则可以采用例2 的方法求E-A的逆矩阵.
是否为零矩阵, 若为零矩阵, 则可以采用例2 的方法求E-A的逆矩阵.
解 容易验证
A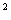 =
= , A
, A =
= , A
, A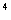 =0
=0
而 (E-A)(E+A+ A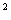 + A
+ A )=E,所以
)=E,所以
(E-A) = E+A+ A
= E+A+ A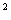 + A
+ A =
= .
.
2.初等变换法
求元素为具体数字的矩阵的逆矩阵,常用初等变换法.如果A可逆,则A可通过初等变换,化为单位矩阵I,即存在初等矩阵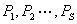 使
使
(1)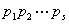 A=I,用A
A=I,用A 右乘上式两端,得:
右乘上式两端,得:
(2) 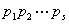 I= A
I= A
比较(1)(2)两式,可以看到当A通过初等变换化为单位矩阵的同时,对单位矩阵I作同样的初等变换,就化为A的逆矩阵A .
.
用矩阵表示(A I)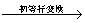 为(I A
为(I A ),就是求逆矩阵的初等行变换法,它是实际应用中比较简单的一种方法.需要注意的是,在作初等变换时只允许作行初等变换.同样,只用列初等变换也可以求逆矩阵.
),就是求逆矩阵的初等行变换法,它是实际应用中比较简单的一种方法.需要注意的是,在作初等变换时只允许作行初等变换.同样,只用列初等变换也可以求逆矩阵.
例1 求矩阵A的逆矩阵.已知A=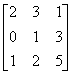 .
.
解 [A I]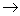

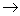

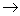
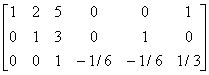
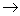
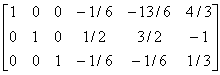
故 A =
= .
.
在事先不知道n阶矩阵是否可逆的情况下,也可以直接用此方法.如果在初等变换过程中发现左边的矩阵有一行元素全为0,则意味着A不可逆,因为此时表明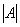 =0,则A
=0,则A 不存在.
不存在.
例2 求A=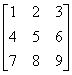 .
.
解 [A E]=
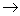
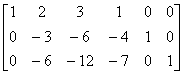
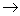
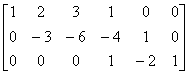 .
.
由于左端矩阵中有一行元素全为0,于是它不可逆,因此A不可逆.
3.伴随阵法
定理 n阶矩阵A=[a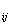 ]为可逆的充分必要条件是A非奇异.且
]为可逆的充分必要条件是A非奇异.且
A =
=

其中A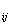 是
是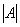 中元素a
中元素a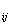 的代数余子式.
的代数余子式.
矩阵 称为矩阵A的伴随矩阵,记作A
称为矩阵A的伴随矩阵,记作A ,于是有A
,于是有A =
= A
A .
.
证明 必要性:设A可逆,由A A =I,有
=I,有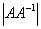 =
=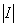 ,则
,则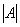
 =
=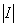 ,所以
,所以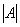
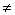 0,即A为非奇异.
0,即A为非奇异.
充分性: 设A为非奇异,存在矩阵
B=
 ,
,
其中
AB=
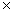


=
 =
= =I
=I
同理可证BA=I.
由此可知,若A可逆,则A =
= A
A .
.
用此方法求逆矩阵,对于小型矩阵,特别是二阶方阵求逆既方便、快阵,又有规律可循.因为二阶可逆矩阵的伴随矩阵,只需要将主对角线元素的位置互换,次对角线的元素变号即可.
若可逆矩阵是三阶或三阶以上矩阵,在求逆矩阵的过程中,需要求9个或9个以上代数余子式,还要计算一个三阶或三阶以上行列式,工作量大且中途难免
出现符号及计算的差错.对于求出的逆矩阵是否正确,一般要通过AA =I来检验.一旦发现错误,必须对每一计算逐一排查.
=I来检验.一旦发现错误,必须对每一计算逐一排查.
4.分块矩阵求逆法
4.1.准对角形矩阵的求逆
命题 设A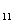 、A
、A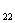 都是非奇异矩阵,且A
都是非奇异矩阵,且A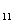 为n阶方阵,A
为n阶方阵,A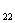 为m阶方阵
为m阶方阵

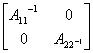
证明 因为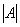 =
= =
=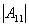
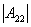
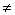 0, 所以A可逆.
0, 所以A可逆.
设A =
= ,于是有
,于是有
 =
= ,
,
其中 X A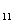 =I
=I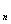 , Y A
, Y A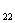 =0,Z A
=0,Z A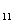 =0,W A
=0,W A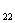 =I
=I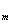 .又因为A
.又因为A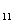 、A
、A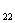 都可逆,用A
都可逆,用A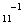 、A
、A 分别右乘上面左右两组等式得:
分别右乘上面左右两组等式得:
X= A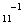 ,Y=0,Z=0,W= A
,Y=0,Z=0,W= A
故 A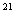 =
= 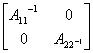
把上述结论推广到每一个子块都是非奇异矩阵的准对角形状矩阵中去,即:
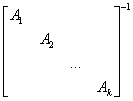 =
=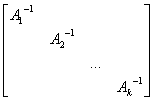
4.2.准三角形矩阵求逆
命题 设A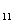 、A
、A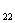 都是非奇异矩阵,则有
都是非奇异矩阵,则有
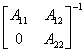 =
=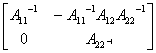
证明 因为
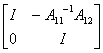 =
=
两边求逆得
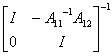
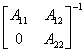 =
=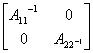
所以 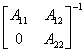 =
=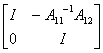
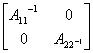
=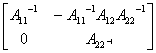
同理可证
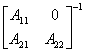 =
=
此方法适用于大型且能化成对角子块阵或三角块阵的矩阵. 是特殊方阵求逆的一种方法,并且在求逆矩阵之前,首先要将已给定矩阵进行合理分块后方能使用.
5.恒等变形法
恒等变形法求逆矩阵的理论依据为逆矩阵的定义,此方法也常用与矩阵的理论推导上.就是通过恒等变形把要求的值化简出来,题目中的逆矩阵可以不求,利用AA =E,把题目中的逆矩阵化简掉。
=E,把题目中的逆矩阵化简掉。
例1 计算(A+4E)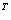 (4E-A)
(4E-A) (16E-A
(16E-A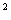 )的行列式,其中 A=
)的行列式,其中 A=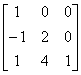
解 令 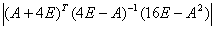 =D
=D
D=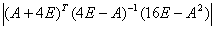
=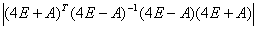
=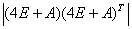 =
=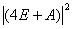 .
.
虽然题目中出现了(4E-A) .但是经过化简之后不再出现此式,因此得
.但是经过化简之后不再出现此式,因此得
D=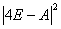 =22500.
=22500.
例2 已知 n阶矩阵A满足A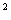 +2A-3E=0.求证:A+4E可逆并求出A+4E的逆.
+2A-3E=0.求证:A+4E可逆并求出A+4E的逆.
证明 把A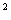 +2A-3E=0变形为A
+2A-3E=0变形为A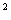 +2A-8E=5E,即
+2A-8E=5E,即
(A+4E)(A-2E)=-5E,可得(A+4E)(-A/5+2E/5)=E,
所以存在一个矩阵B=-A/5+2E/5,使(A+4E)B=E,由定义得A+4E可逆,且
(A+4E)
 =B=-A/5+2E/5.
=B=-A/5+2E/5.
另外,有些计算命题中虽出现逆矩阵,但通过适当的矩阵运算可消去,因而不必急于求出逆矩阵.
6.利用线性方程组求逆矩阵
若n阶矩阵A可逆,则A A =E,于是A
=E,于是A 的第i列是线性方程组AX=E的解,i=1,2,…,n,E是第i个分量是I的单位向量.因此,我们可以去解线性方程组AX=B,
的第i列是线性方程组AX=E的解,i=1,2,…,n,E是第i个分量是I的单位向量.因此,我们可以去解线性方程组AX=B,
其中B=(b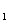 ,b
,b ,…,b
,…,b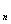 )
)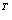 , 然后把所求的解的公式中的b
, 然后把所求的解的公式中的b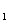 ,b
,b ,…,b
,…,b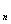 分别用
分别用
E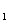 =(1,0,0,…,0),
=(1,0,0,…,0),
E =(0,1,0,…,0),
=(0,1,0,…,0),
……,
E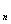 =(0,0,0,…,1)
=(0,0,0,…,1)
代替,便可以求得A 的第1,2,…n列,这种方法在某些时候可能比初等变换法求逆矩阵稍微简一点.下面例子说明该方法的应用.
的第1,2,…n列,这种方法在某些时候可能比初等变换法求逆矩阵稍微简一点.下面例子说明该方法的应用.
例 求矩阵A= 的逆矩阵.
的逆矩阵.
解 设X=(x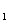 ,x
,x ,x
,x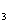 ,x
,x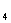 ,x
,x )
)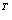 ,B=(b
,B=(b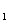 ,b
,b ,b
,b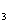 ,b
,b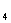 ,b
,b )
)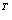 解方程组 AX=B,即:
解方程组 AX=B,即:

解得: 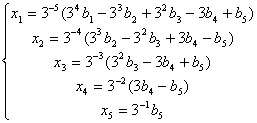
然后把B=(b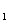 ,b
,b ,…,b
,…,b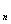 )列,分别用
)列,分别用
E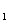 =(1,0,0,…,0),
=(1,0,0,…,0),
E =(0,1,0,…,0),
=(0,1,0,…,0),
……,
E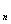 =(0,0,0,…,1)
=(0,0,0,…,1)
代入,得到矩阵A 的第1,2 ,3,4,5列,分别用
的第1,2 ,3,4,5列,分别用
x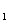 =(
=( ,0,0,0,0)
,0,0,0,0)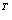 ,
,
x =(3
=(3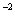 ,
, ,0,0,0)
,0,0,0)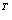 ,
,
x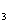 =(3
=(3 ,3
,3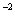 ,
, ,0,0)
,0,0)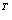 ,
,
x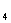 =(3
=(3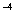 ,3
,3 ,3
,3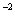 ,
, ,0)
,0)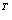 ,
,
x =(3
=(3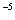 ,3
,3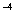 ,3
,3 ,3
,3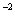 ,
, )
)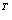
A =
= .
.
这种方法特别适用于线性方程组AX=B比较容易求解的情形,也是很多工程类问题的解决方法.
3.结束语:
以上各种求逆方法只是我的一些粗浅的认识,也许有很多的不当之处,我希望我的这篇文章能给大家带来帮助,能帮助我们更快更准地解决好繁琐的求逆矩阵问题.同时,它还是我们更好的学习线性代数的必备基础知识,认真掌握它,可供我们以后继续在数学方面深造打下坚实的基础.但我很希望各位老师和同学给于指导.能使我的这篇文章更加完善和实用.
参考文献
[1] 北京大学数学系几何与代数教研室代数小组.高等数学[M].北京:高教出版社,2001.
[M]表示参考的是书
[J] 表示参考的是杂志上的论文
分工情况
第一,三部分由 完成
第二部分由 完成
第二篇:求逆矩阵的方法
求逆矩阵的方法与矩阵的秩
一、矩阵的初等行变换
(由定理2.4给出的求逆矩阵的伴随矩阵法,要求计算矩阵A的行列式 值和它的伴随矩阵
值和它的伴随矩阵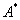 .当A的阶数较高时,它的计算量是很大的,因此用伴随矩阵法求逆矩阵是不方便的.下面介绍利用矩阵初等行变换求逆矩阵的方法.在介绍这种方法之前,先给出矩阵初等行变换的定义.)
.当A的阶数较高时,它的计算量是很大的,因此用伴随矩阵法求逆矩阵是不方便的.下面介绍利用矩阵初等行变换求逆矩阵的方法.在介绍这种方法之前,先给出矩阵初等行变换的定义.)
定义2.13 矩阵的初等行变换是指对矩阵进行下列三种变换:
(1) 将矩阵中某两行对换位置;
(2) 将某一行遍乘一个非零常数k;
(3) 将矩阵的某一行遍乘一个常数k加至另一行.
并称(1)为对换变换,称(2)为倍乘变换,称(3)为倍加变换.
矩阵A经过初等行变换后变为B,用
A B
B
 表示,并称矩阵B与A是等价的.
表示,并称矩阵B与A是等价的.

 (下面我们把)第
(下面我们把)第 行和第j行的对换变换,简记为“ , ”;把第
行和第j行的对换变换,简记为“ , ”;把第 行遍乘k倍的倍乘变换,简记为“ k”;第j行的k倍加至第
行遍乘k倍的倍乘变换,简记为“ k”;第j行的k倍加至第 行上的倍加变换,简记为“ + k”.
行上的倍加变换,简记为“ + k”.
 例如,矩阵 A =
例如,矩阵 A = 
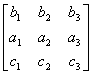
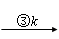

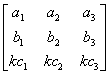
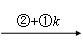

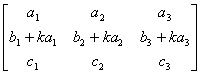
(关于初等矩阵内容请大家自己阅读教材)
二、运用初等行变换求逆矩阵
由定理2.7的推论“任何非奇异矩阵均能经过初等行变换化为单位阵”可知,对于任意一个n阶可逆矩阵A,经过一系列的初等行变换可以化为单位阵I,那么用一系列同样的初等行变换作用到单位阵I上,就可以把I化成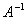 .因此,我们得到用初等行变换求逆矩阵的方法:在矩阵A的右边写上一个同阶的单位矩阵I,构成一个n
.因此,我们得到用初等行变换求逆矩阵的方法:在矩阵A的右边写上一个同阶的单位矩阵I,构成一个n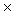 2n矩阵 ( A , I ),用初等行变换将左半部分的A化成单位矩阵I,与此同时,右半部分的I就被化成了
2n矩阵 ( A , I ),用初等行变换将左半部分的A化成单位矩阵I,与此同时,右半部分的I就被化成了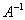 .即
.即
( A , I ) ( I ,
( I , 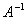 )
)
例1 设矩阵 A = 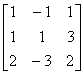
求逆矩阵 .
.
解 因为
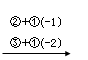 [A , I ] =
[A , I ] =

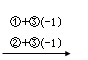
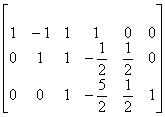

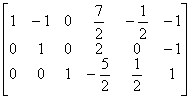
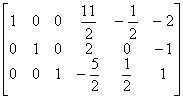
所以 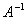 =
= 
所求逆矩阵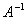 是否正确,可以通过计算乘积矩阵A
是否正确,可以通过计算乘积矩阵A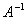 进行验证.如果A
进行验证.如果A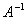 =I成立,则
=I成立,则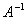 正确,否则不正确.
正确,否则不正确.
对给定的n阶矩阵A,用上述方法也可以判断A是否可逆.即在对矩阵[ A , I ] 进行初等行变换的过程中,如果[ A , I ]中的左边的方阵出现零行,说明矩阵A是奇异的,即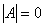 ,可以判定A不可逆;如果[ A , I ]中的左边的方阵被化成了单位阵I,说明A是非奇异的,可以判定A是可逆的,而且这个单位矩阵I右边的方阵就是A的逆矩阵
,可以判定A不可逆;如果[ A , I ]中的左边的方阵被化成了单位阵I,说明A是非奇异的,可以判定A是可逆的,而且这个单位矩阵I右边的方阵就是A的逆矩阵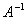 ,它是由单位矩阵I经过同样的初等行变换得到的.
,它是由单位矩阵I经过同样的初等行变换得到的.
例2 设矩阵 A = 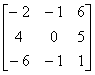 ,问A是否可逆?
,问A是否可逆?
解 因为
[ A , I ] =
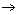
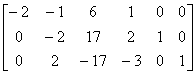
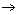

[ A , I ]中的左边的矩阵A经过初等行变换后出现零行,所以矩阵A是奇异的,A不可逆.
(下面利用矩阵求逆运算求解矩阵方程.)
例3 解矩阵方程AX = B,其中 A =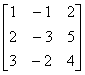 ,B =
,B =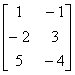
解 [思路] 如果矩阵A可逆,则在矩阵方程AX = B等号的两边同时左乘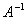 ,可得
,可得
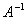 AX =
AX = 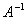 B, X =
B, X = 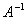 B
B
因此,先用初等行变换法判别A是否可逆,若可逆,则求出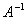 ,然后计算
,然后计算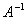 B,求出X .
B,求出X .
因为 [ A , I ] = 

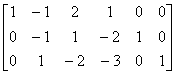



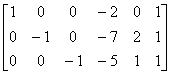

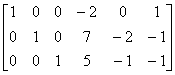
所以 A可逆,且 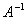 =
=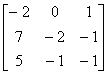
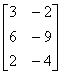
X = 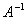 B =
B = 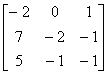
 =
=
三、矩阵的秩
前面给出了利用矩阵行列式 判别方阵A是否可逆的方法,除了这种方法外,还可以利用矩阵A的特征之一——矩阵的秩来判别方阵A的可逆性.
判别方阵A是否可逆的方法,除了这种方法外,还可以利用矩阵A的特征之一——矩阵的秩来判别方阵A的可逆性.
矩阵的秩是线性代数中非常有用的一个概念,它不仅与讨论可逆矩阵的问题有密切关系,而且在讨论线性方程组的解的情况中也有重要应用.
在给出矩阵的秩的概念之前,先要定义矩阵的子式.
定义2.15 在矩阵A中,位于任意选定的k行、k列交叉点上的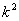 个元素,按原来次序组成的k阶子阵的行列式,称为A的一个k阶子式.如果子式的值不为零.就称为非零子式.
个元素,按原来次序组成的k阶子阵的行列式,称为A的一个k阶子式.如果子式的值不为零.就称为非零子式.
例4 设矩阵 A=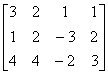
取其第一、二行与第二、四列交叉点上的4个元素按原次序组成行列式

称为A的一个二阶子式,而且是它的非零子式.
定义2.16 矩阵A的非零子式的最高阶数称为矩阵A的秩,记作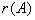 或秩(A ) .
或秩(A ) .
规定:零矩阵O的秩为零,即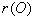 = 0.
= 0.
例4中的矩阵已经有一个二阶非零子式,通过计算可知,矩阵A的所有三阶子式均为零,(该矩阵没有四阶子式),所以 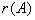 = 2 .
= 2 .
例5 设A为n阶非奇异矩阵,求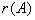 .
.
解 由于A为非奇异矩阵,即A对应的行列式 ,所以A有n阶非零子式,故
,所以A有n阶非零子式,故 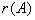 = n .
= n .
例5的逆命题亦成立,即对一个n阶方阵A,若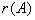 = n,则A必为非奇异的.
= n,则A必为非奇异的.
因此n阶方阵A为非奇异的等价于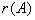 = n.
= n.
称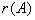 = n的n阶方阵为满秩矩阵.
= n的n阶方阵为满秩矩阵.
用定义求矩阵的秩,需要计算它的子式,计算量常常是较大的.利用教材中的定理2.10计算矩阵的秩是比较方便的.
定理2.10 设A为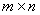 矩阵,则
矩阵,则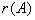 = k的充分必要条件为:通过初等行变换能将A化为具有k个非零行的阶梯阵.
= k的充分必要条件为:通过初等行变换能将A化为具有k个非零行的阶梯阵.
例如,阶梯阵
A = , B =
, B =
因为A的非零行有二行,而B 的非零行有三行,所以A的秩等于2,B 的秩等于3,即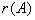 = 2,
= 2, = 3.
= 3.
那么一个矩阵经过初等行变换化成阶梯阵后,它的秩是否会发生变化呢?不会的.教材中的定理2.9已经说明这一点.
定理2.9 矩阵经过初等行变换后,其秩不变. (证明见教材)
定理2.10给了我们求矩阵的秩的一种简便方法,即利用初等行变换将一个矩阵A化成阶梯阵,然后算出矩阵A的秩.
例6 设矩阵
A =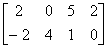 , B =
, B =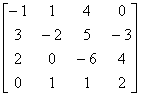
求 ,
, ,
, .
.
解 因为 A = 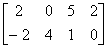
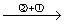
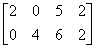
所以 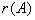 = 2
= 2
因为 B =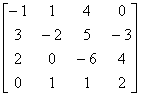
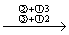

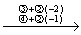

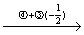

所以  = 3
= 3
因为 AB = 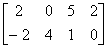
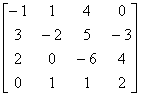 =
=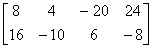
AB =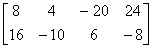
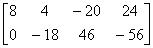
所以  = 2
= 2
由例6可知,乘积矩阵AB的秩不大于两个相乘的矩阵A , B的秩,即 
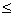
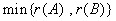 .
.
例7 设矩阵 A =
求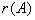 和
和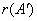 .
.
解 因为 A =
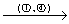



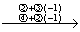

所以 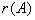 =3
=3
同理可得 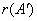 =3
=3
由例7可知,矩阵A与它的转置矩阵 的秩相等. 可以证明例6,例7的结论具有一般性.
的秩相等. 可以证明例6,例7的结论具有一般性.
定理2.11 设A为m n矩阵,则
n矩阵,则
(1)  ;
;
(2) 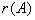 =
=