第一章：
1. 算法定义：算法是若干指令的有穷序列，满足性质：
(1)输入：有外部提供的量作为算法的输入。
(2)输出：算法产生至少一个量作为输出。
(3)确定性：组成算法的每条指令是清晰，无歧义的。
(4)有限性：算法中每条指令的执行次数是有限的，执行每条指令的时间也是有限的。
2. 程序定义：程序是算法用某种程序设计语言的具体实现。可以不满足算法的性质(4)。
3. 算法复杂性分为时间复杂性和空间复杂性。
4. 可操作性最好且最有使用价值的是最坏情况下的时间复杂性。
5. O(n)定义：存在正的常数C和自然数N0，当N>=N0时有f(N)<=Cg(N),则称函数f(N)当N充分大时有上界，记作f(N)=O(g(n)).
6. ?(n)定义：存在正的常数C和自然数N0，当N>=N0时有f(N)>=Cg(N),则称函数f(N)当N充分大时有上界，记作f(N)=?(g(n)).
7. 
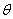(n)定义:当f(n)=O(g(n))且f(N)=?(g(n))，记作f(N)=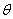(g(n))，称为同阶。
8. 求下列函数的渐进表达式：3n2+10n ~~~O(n2) n2/10+2n~~~O(2n)
21+1/n~~~O(1) logn3~~~O(logn) 10log3n~~~O(n)
9. 从低到高渐进阶排序：2 logn n2/3 20n 4n2 3n n!
第二章：
1. 分治法的设计思想：将一个难以直接解决的问题，分割成一些规模较小的相同问题，以便各个击破分而治之。
2. 例1 Fibonacci数列 代码（注意边界条件）。
int fibonacci(int n)
{
if (n <= 1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
3. Ackerman函数双递归。
A(1,1)代入求值。
A(1,1)=A(A(0,1),0)=A(1,0)=2
4. 全排列的递归算法代码。
void Perm(int a[],int n,int k)
{
if(n==k){
for(int i=0;i<n;i++)
cout<<a[i]<<” ”;
cout<<endl;
return ;
}
for(int i=k;i<n;i++){
Swap(a[i].a[k]);
Perm(a,n,k+1);
Swap(a[i],a[k]);
}
return ;
}
5. Hanoi塔问题的递归算法与时间复杂度。
void Hanoi(int n,int from,int to,int other)//将n个盘子从from借助other到达to
{
if(n<=0)
return;
Hanoi(n-1,from,other,to);//将n-1个盘子从from借助to到达other,此时n-1个盘子都在other上，1 //个盘子在from上。
Move(1,from,to);//将from上的那个盘子移动到to上。此时from为空。
Hanoi(n-1,other,to,from);//将other上的n-1个盘子借助from移动到to上。此时to上有n个盘子。
}
O(2n)
6. 整数划分问题的递归公式。
分解整数n为n1,n2…,以降序排列，q(n,m)表示最大的n1<=m的划分方法数。
q(n,m)=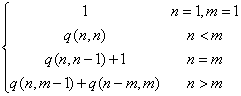
7. T(n)=kT(n/m)+nd 。k表示划分子问题的个数，m表示减小问题的规模，nd表示分割组合子问题所需的时间复杂度。
结论：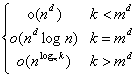
8. 二分搜索代码及变形P35(答案是FFFFTFF)。
int BinarySearch(int a[], int x, int l, int r)//a数组的搜索边界为[l,r]
{
while (r >= l){
int m = (l+r)/2;
if (x == a[m]) return m;
if (x < a[m])
r = m-1;
else
l = m+1;
}
return -1;
}
9. 大整数乘法及Strassen矩阵乘法的时间复杂度。（运用本节7的结论）
大整数乘法将X=[A B],Y=[C D]。XY=AC2N+((A-B)(D-C)+AC+BD)2N/2+BD（不记）。子问题个数k为三次乘法AC\BD\(A-B)(C-D),问题规模减小了一半，即m=2。分开合并花费O(n).所以，时间复杂度为O(nlog3).
Strassen矩阵乘法将矩阵以“田”字分割矩阵后相乘，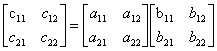
T(n)=7T(n/2)+O(n2)，所以时间复杂度为O(nlog7).
10. 棋盘覆盖过程及时间复杂度。
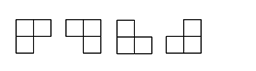
有一个2 k*2 k的特殊方格地面，因为它有一个地板不能铺设，用黑色标出。现在用如下四种地板进行铺设。
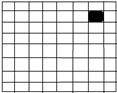
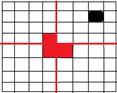
原图，田字划分后在中间位置铺设一块地板，使得每个四分之一部分都有一块被涂色的地板。将问题分成了4个相同的子问题。在每个四分之一部分，重复进行田字划分和中间铺设地板，最终可以完成该问题。
N=2k,K=4,m=2,合并分解复杂度为O(1),所以T(n)=O((2k)log24)=O(4k)
11. 合并排序、快速排序、线性时间选择的思想、代码、时间复杂度。
合并排序O(nlogn)：
void mergeSort(int a[], int left, int right)
{
if (left<right) {//至少有2个元素
int i=(left+right)/2; //取中点
mergeSort(a, left, i);
mergeSort(a, i+1, right);
merge(a, b, left, i, right); //合并到数组b
copy(a, b, left, right); //复制回数组a
}
}
void merge(int a[],int b[],int l,int m,int r)
{
int i=l,j=m+1,k=l;
while(i<=m&&j<=r){
if(a[i]<a[j]) b[k++]=a[i++];
else b[k++]=a[j++];
}
while(i<=m)
b[k++]=a[i++];
while(j<=r)
b[k++]=a[j++];
return ;
}
快速排序O(nlogn)：
void QuickSort (int a[], int p, int r)
{
if (p<r) {
int q=Partition(a,p,r);
QuickSort (a,p,q-1); //对左半段排序
QuickSort (a,q+1,r); //对右半段排序
}
}
int Partition (int a[], int p, int r)
{
int i = p, j = r + 1;
int x=a[p];
while (true) {
while (a[++i] <x);
while (a[- -j] >x);
if (i >= j) break;
Swap(a[i], a[j]);
}
a[p] = a[j];
a[j] = x;
return j;
}
线性时间选择O(n)：
int RandomizedSelect(int a[],int p,int r,int k)//在数组a[p]到a[r]中选择第k大的数
{
if (p==r) return a[p];//如果该数组只有一个元素了就直接返回该元素
int i=RandomizedPartition(a,p,r),//将a数组按照快速排序的思想分成两份，下标小于i的元素值都小于a[i]，下标大于i的元素值都大于a[i],但其本身没有排序。
j=i-p+1;//j为比a[i]小的元素的个数
if (k<=j) return RandomizedSelect(a,p,i,k);//如果k<=j，说明第k大元素在前半部分
else return RandomizedSelect(a,i+1,r,k-j);//否则在后半部分寻找k-j大的元素
}
12. 循环赛日程表制作过程。
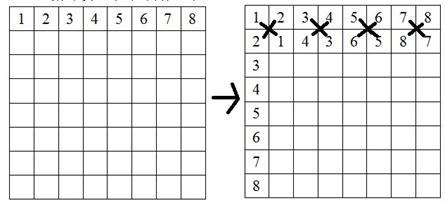
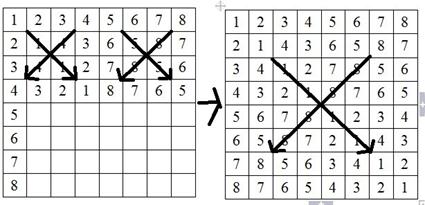
第三章：
1. 矩阵连乘问题过程及递归定义。
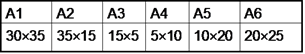
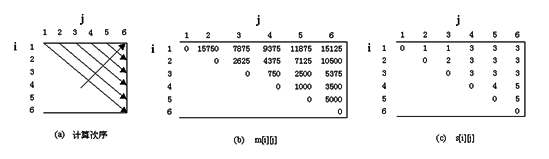
2. 动态规划解题步骤：
（1）找出最优解的性质，并刻画其结构特征。
（2）递归的定义最优值。
（3）以自底向上的方式计算出最优值。
（4）根据计算最优值时得到的信息，构造最优解。
3. 最优子结构性质定义：当问题的最优解包含着其子问题的最优解。
4. 最长公共子序列的递归定义及时间复杂度。
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ，则
(1)若xm=yn，则zk=xm=yn，且zk-1是xm-1和yn-1的最长公共子序列。
(2)若xm≠yn且zk≠xm，则Z是xm-1和Y的最长公共子序列。
(3)若xm≠yn且zk≠yn，则Z是X和yn-1的最长公共子序列。
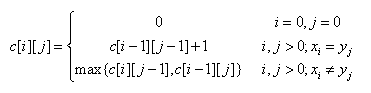
当xi=yj时，表示找到一个公共数字，则c[i][j]=c[i-1][j-1]+1;
当xi！=yj时，那么该情况下的最长序列数为c[i][j]=max{c[i-1][j],c[i][j-1]}
5. 最大子段和的递归定义及时间复杂度。
已知序列a[1:n]，找到最大的连续的子段和。
若记b[j]=max{åa[k]}, (k=1,…j; 1≤j≤n)
即b[j] 为a[1],…,a[j] 中的最大子段和。
则原问题的最大子段和为 max b[j] (1≤j≤n).
由此可得计算b[j]的动态规划递归式
b[j]=max{b[j-1]+a[j], a[j]}, 1≤j≤n
O(n)。
6. 0-1背包问题思想及代码。
M(i,j)定义为放入第i个物品时，还剩余j个重量，最大的价值量。如果剩余重量j<wi时，则第i个物品不能放进去，所以m[i][j]=m[i+1][j]。如果j>=wi时，最大价值应该是两者之间的最大值（m[i+1][j]不放第i个物品，m[i+1][j-w[i]]放入第i个物品）。
int Knapsack(int v[],int w[],int c,int n,int **m)
{
int jMax = min(w[n-1]-1,c);
for(int j=0; j<=jMax; j++)
m[n-1][j]=0;
for(int j=w[n-1]; j<=c; j++)m[n-1][j]=v[n-1];
for(int i=n-1; i>1; i--)
{
jMax = min(w[i]-1,c);
for(int j=0; j<=jMax; j++)m[i][j]=m[i+1][j];
for(int j=w[i]; j<=c; j++)
m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
m[1][c]=m[2][c];
if(c>=w[1])m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);
return m[1][c];
}
第四章：
1. 活动安排问题计算过程及贪心性质证明。
例：设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下：
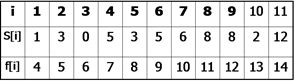
答：将所有活动的结束时间按照降序排列，第1个选中。如果s[j]>=f[i]，j>i则第j个物品可以选中。即后面的任务的开始时间大于等于最后一个任务的结束时间时，就选中该任务。
证明：P104最后一段。
2. 贪心选择性质定义：所求问题的整体最优解可以通过一系列局部最优的选择得到。
3. Dijkstra单元最短路径迭代过程及代码。
其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
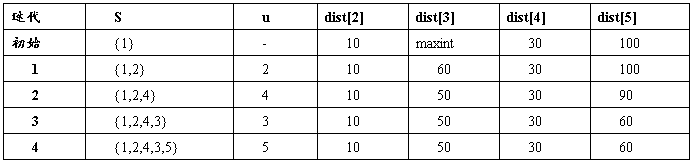
初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。
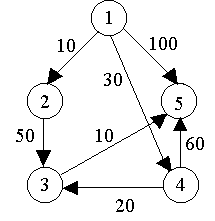
Dijkstra算法的迭代过程：
代码:
void Dijkstra(int n,int v,Type dist[],Type c[][])
{
bool s[ maxint];
for(int i=1;i<=n;i++){
dist[i]=c[v][i];
s[i]=false;
if(dist[i]==maxint) prev[i]=0;
else prev[i]=v;
}
dist[v]=0;s[v]=true;
for(int i=1;i<n;i++)
{
int temp=maxint;
int u=v;
for(int j=1;j<=n;j++)
if(!s[j]&&(dist[j]<temp)) {u=j;temp=dist[j];}
s[u]=true;
for(int j=1;<=n;j++)
if(!s[j]&&(c[u][j]<maxint)){
Type newdist=dist[u]+c[u][j];
if(newdist<dist[j]) {dist[j]= newdist ;prev[j]=u;}
}
}
}
4. Prim最小生成树选边过程，Kruskal最小生成树选边过程。什么情况下选择Prim？什么情况下选择Kruskal？
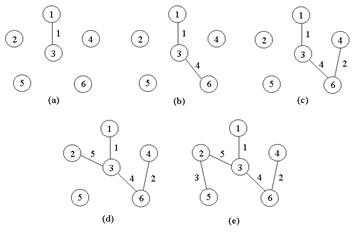Prim:
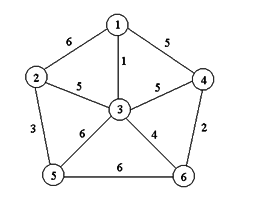
Kruskal:
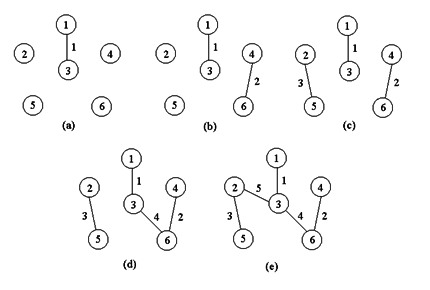
当e=?(n2)时选择Prim算法，如果e=o(n2)时选择Kruskal算法。
5. 多机调度问题示例。
例如，设7个独立作业{1,2,3,4,5,6,7}由3台机器M1，M2和M3加工处理。各作业所需的处理时间分别为{2,14,4,16,6,5,3}。按算法greedy产生的作业调度如下图所示，所需的加工时间为17。
答：按照处理时间排序的作业号为{4,2,5,6,3,7,1},按照此顺序进行安排4,2,5，最早结束的是M3，所以将6安排在M3，然后最早结束的是M3，将3安排在M3…以此类推。
第五章：
1. 迭代回溯、递归回溯代码框架。
递归回溯代码框架:
void Backtrack(int t)
{
if(t>n) Output(x);
else
for(int i=f(n,t);i<=g(n,t);i++){
x[t]=h(i);
if(constraint(t)&&Bound(t)) Backtrack(t+1);//约束条件、边界条件
}
}
迭代回溯代码框架：
void IterativeBacktrack(void)
{
int t=1;
while(t>0)
{
if(f(n,t)<=g(n,t))
for(int i= f(n,t);i<= g(n,t);i++)
{
x[t]=h(i);
if(constraint(t)&&Bound(t)){
if(solution(t))Output(x);
else t++;
}
}
else t--;
}
}
2. 子集树排列树代码框架。
子集树代码框架：
void BackTrack(int t)
{
if(t>n) Output(x);
else
for(int i=0;i<=n;i++)
{
x[t]=i;
if(constraint(t)&&Bound(t))
Backtrack(t+1);
}
}
排列树代码框架：
void BackTrack(int t)
{
if(t>n) Output(x);
else
for(int i=t;i<=n;i++)
{
swap(x[t],x[i]);
if(constraint(t)&&Bound(t))
Backtrack(t+1);
swap(x[t],x[i]);
}
}
3. 回溯法最优装载问题思想。
采用下面的策略可得到最优装载方案。
(1)首先将第一艘轮船尽可能装满；
(2)将剩余的集装箱装上第二艘轮船。
第一艘轮船的总载重量为c,n件物品的每一个重量为wi。选择一个子集使得物品总重小于等于c且尽量装满。由此可知，装载问题等价于以下特殊的0-1背包问题。
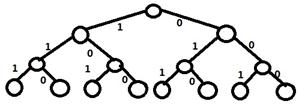
子集树第i层的边表示第i件物品是否放入轮船，如果是1则表示放入，是0表示不放入。
约束函数：如果该节点的总重量大于c，则剩余子树都不能够成为可行解，直接剪掉这些子树。
限界函数：如果该节点一下的总重量加上此时的已有载重量的总和都不能够达到曾经已经找到的最优值，则此节点之后的子树也可以不再搜索。
用回溯法设计解装载问题的O(2n)计算时间算法。在某些情况下该算法优于动态规划算法。
4. 符号三角形问题思想。
下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”，2个异号下面都是“-”。
+ + - + - + +
+ - - - - +
- + + + -
- + + -
- + -
- -
+
在一般情况下，符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。
可以看出只要第一行的符号形式确定后，这个三角形的形状就确定了。因此只要遍历第一行能够出现的各种情况，遍历过程中确定当前情况下的三角形是否符合要求。这个问题便可解决。
（1）用0代表‘-’，1代表‘+’;则此问题的解空间可以看做是一颗子集树。
（2）剪枝函数为当前阶段，'+'的个数和’-‘的个数<=(N+1)*（N）/4
解题思路：
n 1、不断改变第一行每个符号，搜索符合条件的解，可以使用递归回溯
n 2、因为两种符号个数相同，可以对题解树剪枝，
当所有符号总数为奇数时无解，当某种符号超过总数一半时无解
复杂度分析
计算可行性约束需要O(n)时间，在最坏情况下有 O(2n)个结点需要计算可行性约束，故解符号三角形问题的回溯算法所需的计算时间为 O(n2n)。
5. N后问题（重点）思想及代码。
对每一列进行迭代t（0<t<=n），x[t]保存第t列的棋子放置的位置。所以x[t]的取值范围是[1,n]。针对x[t]枚举赋值[1,n]，然后判断可不可以这样放置。
class Queue{
friend void nQueue(int);//该函数可以调用Queue的私有成员
private:
bool Place(int t);//是否可以放在第x[t]的位置，可以防止就返回true
void Backtrack(int t);//迭代函数
int n;//n后棋盘的边长
int *x;//解
long sum;//可行解的个数
};
Queue X;
bool Queue::Place(int k)
{
for(int j=1;j<k;j++)
if(abs(k-j)==abs(x[j]-x[k])||(x[j]==x[k]))//如果出现边界水平或者垂直或者对角线，则返回false
return false;
return true;
}
void Queue::Backtrack(int t)
{
if(t>n)//已经迭代到最后一层，说明已经找到了一种可行解
{
sum++;
for(int i=1;i<=n;i++)
cout<<"("<<i<<","<<x[i]<<")";
cout<<endl;
}
else
for(int i=1;i<=X.n;i++)//可以放在1-n的任意位置，将该位置作为可行解赋值后，如果可以放置，则进行下一列的迭代，否则换一个位置重新检测。
{
X.x[t]=i;
if(Place(t))
{
Backtrack(t+1);
}
}
}
void nQueue(int n)
{
X.n=n;
X.sum=0;
int *p = new int[n+1];
for(int i=0;i<=n;i++)
p[i]=0;
X.x=p;
X.Backtrack(1);
cout<<"共有"<<X.sum<<"种方案！"<<endl;
delete []p;
}
6. 0-1背包问题思想。
第六章：
1. 回溯法与分支限界法区别。
回溯法的实质就是深度优先搜索，分支限界法的实质就是广度优先搜索。唯一区别就是约束函数和限界函数。
2. 优先队列式分支限界法解0-1背包问题的状态树。
3. 分支限界法分类：队列式分支限界法和优先队列式分支限界法。
4. 装载问题优先队列式分支限界法的状态树。