
第二篇:高中数学 学案48直线、圆的位置关系
学案48 直线、圆的位置关系
导学目标: 1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题.3.在学习过程中,体会用代数方法处理几何问题的思想.

自主梳理
1.直线与圆的位置关系
位置关系有三种:________、________、________.
判断直线与圆的位置关系常见的有两种方法:
①代数法:利用判别式Δ,即直线方程与圆的方程联立方程组消去x或y整理成一元二
>0?,??次方程后,计算判别式Δ=b2-4ac?=0? ,
??<0? .
②几何法:利用圆心到直线的距离d和圆半径r的大小关系:
d<r?________,d=r?________,d>r?________.
2.圆的切线方程
若圆的方程为x2+y2=r2,点P(x0,y0)在圆上,则过P点且与圆x2+y2=r2相切的切线方程为______________________.
注:点P必须在圆x2+y2=r2上.
经过圆(x-a)2+(y-b)2=r2上点P(x0,y0)的切线方程为________________________.
3.计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
(2)代数方法
运用韦达定理及弦长公式
AB=1+k|xA-xB|=?1+k?[?xA+xB?-4xAxB].
说明:圆的弦长、弦心距的计算常用几何方法.
4.圆与圆的位置关系
(1)圆与圆的位置关系可分为五种:________、________、________、________、________. 判断圆与圆的位置关系常用方法:
(几何法)设两圆圆心分别为O1、O2,半径为r1、r2 (r1≠r2),则O1O2>r1+r2________;O1O2=r1+r2________;|r1-r2|<O1O2<r1+r2________;O1O2=|r1-r2|________;0≤|O1O2|<|r1-r2|________.
(2)已知两圆x2+y2+D1x+E1y+F1=0和x2+y2+D2x+E2y+F2=0相交,则与两圆共交点的圆系方程为____________________________________________________________,其中λ为λ≠-1的任意常数,因此圆系不包括第二个圆.
当λ=-1时,为两圆公共弦所在的直线,方程为(D1-D2)x+(E1-E2)y+(F1-F2)=0. 自我检测
1.(2010·江西)直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若MN≥3,则k的取值范围是________.
2.圆x2+y2-4x=0在点P(13)处的切线方程为______________.
3.圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0的公切线有________条.
4.过点(0,1)的直线与x2+y2=4相交于A、B两点,则AB的最小值为________.
5.若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是
______________.

探究点一 直线与圆的位置关系
例1 已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有PM=PO,求使得PM取得最小值时点P的坐标.
变式迁移1 从圆C:(x-1)2+(y-1)2=1外一点P(2,3)向该圆引切线,求切线的方程及过两切点的直线方程.
探究点二 圆的弦长、中点弦问题
例2 已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.
(1)若直线l过点P且被圆C截得的线段长为3,求l的方程;
(2)求过P点的圆C的弦的中点的轨迹方程.
变式迁移2 已知圆C:x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)证明:不论k取何值,直线和圆总有两个不同交点;
(2)求当k取什么值时,直线被圆截得的弦最短,并求这条最短弦的长.
探究点三 圆与圆的位置关系
例3 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,m为何值时,
(1)圆C1与圆C2相外切;(2)圆C1与圆C2内含.
变式迁移3 已知⊙A:x2+y2+2x+2y-2=0,⊙B:x2+y2-2ax-2by+a2-1=0.当a,b变化时,若⊙B始终平分⊙A的周长,求:
(1)⊙B的圆心B的轨迹方程;
(2)⊙B的半径最小时圆的方程.
探究点四 综合应用
例4 已知圆C:x2+y2-2x+4y-4=0.问在圆C上是否存在两点A、B关于直线y=kx-1对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程;若不存在,说明理由.
变式迁移4 已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1相交于M、N两点.
(1)求实数k的取值范围;
→→(2)若O为坐标原点,且OM·ON=12,求k的值.

1.求切线方程时,若知道切点,可直接利用公式;若过圆外一点求切线,一般运用圆
心到直线的距离等于半径来求,但注意有两条.
2.解决与弦长有关的问题时,注意运用由半径、弦心距、弦长的一半构成的直角三角形,也可以运用弦长公式.这就是通常所说的“几何法”和“代数法”.
3.判断两圆的位置关系,从圆心距和两圆半径的关系入手.

(满分:90分)
一、填空题(每小题6分,共48分)
1.直线l:y-1=k(x-1)和圆x2+y2-2y=0的位置关系是________.
2.直线3x-y+m=0与圆x2+y2-2x-2=0相切,则实数m=______________.
3.过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长为________.
4.若圆(x-3)2+(y+5)2=r2上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是______________.
5.若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦的长为3,则a=________.
6.已知点A是圆C:x2+y2+ax+4y-5=0上任意一点,A点关于直线x+2y-1=0的对称点也在圆C上,则实数a=________.
7.设直线3x+4y-5=0与圆C1:x2+y2=4交于A,B两点,若圆C2的圆心在线段AB上,且圆C2与圆C1相切,切点在圆C1的劣弧AB上,则圆C2的半径的最大值是________.
8.(2010·全国Ⅰ改编)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切
→→点,那么PA·PB的最小值为____________.
二、解答题(共42分)
9.(14分)圆x2+y2=8内一点P(-1,2),过点P的直线l的倾斜角为α,直线l交圆于A、B两点.
3π(1)当α=AB的长; 4
(2)当弦AB被点P平分时,求直线l的方程.
10.(14分)自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
11.(14分)已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.求:
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)m=45时两圆的公共弦所在直线的方程和公共弦的长.
学案48 直线、圆的位置关系
答案
自主梳理
1.相切 相交 相离 ①相交 相切 相离 ②相交 相切 相离 2.x0x+y0y=r2 (x0-a)(x-a)+(y0-b)(y-b)=r2 4.(1)外离 外切 相交 内切 内含 外离 外切 相交 内切 内含 (2)(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0
自我检测
3-,0? 2.x-3y+2=0 3.2 4.23 1.??4?
5.x-y-3=0
课堂活动区
例1 解题导引 (1)过点P作圆的切线有三种类型:
当P在圆外时,有2条切线;
当P在圆上时,有1条切线;
当P在圆内时,不存在.
(2)利用待定系数法设圆的切线方程时,一定要注意直线方程的存在性,有时要进行恰当分类.
(3)切线长的求法:
过圆C外一点P作圆C的切线,切点为M,半径为R,
则PM=PC-R.
解 (1)将圆C配方得(x+1)2+(y-2)2=2.
①当直线在两坐标轴上的截距为零时,设直线方程为y=kx, |k+2|由2,解得k=6,得y=6)x. 1+k②当直线在两坐标轴上的截距不为零时,
设直线方程为x+y-a=0, |-1+2-a|由2, 2
得|a-1|=2,即a=-1,或a=3.
∴直线方程为x+y+1=0,或x+y-3=0.
综上,圆的切线方程为y=(2+6)x,或y=(26)x,
或x+y+1=0,或x+y-3=0.
(2)由PO=PM,
222得x21+y1=(x1+1)+(y1-2)-2,
整理得2x1-4y1+3=0.
即点P在直线l:2x-4y+3=0上.
当PM取最小值时,即OP取得最小值,直线OP⊥l,
∴直线OP的方程为2x+y=0.
??2x+y=0,33?. 解方程组?得点P的坐标为??105??2x-4y+3=0,?
变式迁移1 解 设圆切线方程为y-3=k(x-2),
|k+2-2k|即kx-y+3-2k=0,∴1, k+1
3∴kx=2. 4
∴切线方程为x=2和3x-4y+6=0.
3-1圆心C为(1,1),∴kPC=2, 2-1
1∴过两切点的直线斜率为-,又x=2与圆交于(2,1), 2
∴过切点的直线为x+2y-4=0.
例2 解题导引 (1)有关圆的弦长的求法:
已知直线的斜率为k,直线与圆C相交于A(x1,y1),B(x2,y2)两点,点C到l的距离为d,圆的半径为r.
方法一 代数法:弦长AB1+k|x2-x1|
=1+k?x1+x2?-4x1x2;
方法二 几何法:弦长AB=
r-d. (2)有关弦的中点问题:
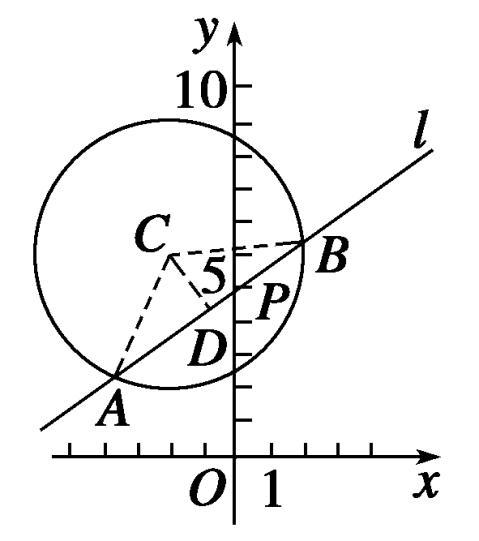
圆心与弦的中点连线和已知直线垂直,利用这条性质可确定某些等量关系. 解 (1)
如图所示,AB=3,取AB的中点D,连结CD,则CD⊥AB,连结AC、BC, 则AD=23,AC=4,
在Rt△ACD中,可得CD=2.
当直线l的斜率存在时,设所求直线的斜率为k,则直线的方程为y-5=kx, 即kx-y+5=0.
|-2k-6+5|由点C到直线AB的距离公式,得=2, k+?-1?3解得k=. 4
3当k=l的方程为3x-4y+20=0. 4
又直线l的斜率不存在时,也满足题意,
此时方程为x=0.
∴所求直线的方程为3x-4y+20=0或x=0.
(2)设过P点的圆C的弦的中点为D(x,y),
→→则CD⊥PD,即CD·PD=0,
(x+2,y-6)·(x,y-5)=0,
化简得所求轨迹方程为x2+y2+2x-11y+30=0.
变式迁移2 (1)证明 由kx-y-4k+3=0,
得(x-4)k-y+3=0.
∴直线kx-y-4k+3=0过定点P(4,3).
由x2+y2-6x-8y+21=0,
即(x-3)2+(y-4)2=4,
又(4-3)2+(3-4)2=2<4.
∴直线和圆总有两个不同的交点.
3-4(2)解 kPC==-1. 4-3
可以证明与PC垂直的直线被圆所截得的弦AB最短,因此过P点斜率为1的直线即为
|3-4-1|所求,其方程为y-3=x-4,即x-y-1=0.PC=2, ∴AB=AC-PC=2.
例3 解题导引 圆和圆的位置关系,从交点个数也就是方程组解的个数来判断,有时得不到确切的结论,通常还是从圆心距d与两圆半径和、差的关系入手.
解 对于圆C1与圆C2的方程,经配方后
C1:(x-m)2+(y+2)2=9;
C2:(x+1)2+(y-m)2=4.
(1)如果C1与C2外切,
?m+1?+?-2-m?=3+2.
(m+1)2+(m+2)2=25.
m2+3m-10=0,解得m=-5或m=2.
(2)如果C1与C2内含,
?m+1?+?m+2?<3-2.
(m+1)2+(m+2)2<1,m2+3m+2<0,
得-2<m<-1,
∴当m=-5或m=2时,圆C1与圆C2外切;
当-2<m<-1时,圆C1与圆C2内含.
变式迁移3 解 (1)两圆方程相减得公共弦方程
2(a+1)x+2(b+1)y-a2-1=0. ①
依题意,公共弦应为⊙A的直径,
将(-1,-1)代入①得a2+2a+2b+5=0. ②
??x=a设圆B的圆心为(x,y),∵?, ?y=b?
∴其轨迹方程为x2+2x+2y+5=0.
(2)⊙B方程可化为(x-a)2+(y-b)2=1+b2.
1由②得b[(a+1)2+4]≤-2,∴b2≥4,b2+1≥5. 2
当a=-1,b=-2时,⊙B半径最小,
∴⊙B方程为(x+1)2+(y+2)2=5.
例4 解题导引 这是一道探索存在性问题,应先假设存在圆上两点关于直线对称,由垂径定理可知圆心应在直线上,以AB为直径的圆经过原点O,应联想直径所对的圆周角为直角利用斜率或向量来解决.因此能否将问题合理地转换是解题的关键.
解 圆C的方程可化为(x-1)2+(y+2)2=9,
圆心为C(1,-2).
假设在圆C上存在两点A、B,则圆心C(1,-2)在直线y=kx-1上,即k=-1.于是可知,kAB=1.
设lAB:y=x+b,代入圆C的方程,
整理得2x2+2(b+1)x+b2+4b-4=0,
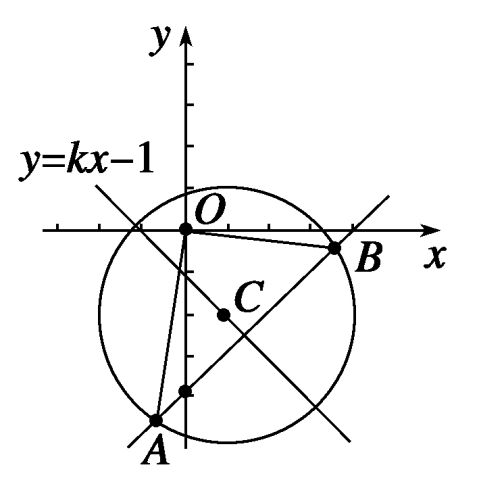
Δ=4(b+1)-8(b+4b-4)>0,b+6b-9<0,
解得-3-32<b<-3+32.
设A(x1,y1),B(x2,y2),
则x1+x2=-b-1,
1x1x2=2+2b-2. 2
由OA⊥OB,知x1x2+y1y2=0,
也就是x1x2+(x1+b)(x2+b)=0,
∴2x1x2+b(x1+x2)+b2=0,
∴b2+4b-4-b2-b+b2=0,化简得b2+3b-4=0, 解得b=-4或b=1,均满足Δ>0.
即直线AB的方程为x-y-4=0,或x-y+1=0. 变式迁移4 解 (1)∵直线l过点A(0,1)且斜率为k, ∴直线l的方程为y=kx+1.
将其代入圆C:(x-2)2+(y-3)2=1,
得(1+k2)x2-4(1+k)x+7=0.①
由题意:Δ=[-4(1+k)]2-4×(1+k2)×7>0, 474+7得<k33
(2)设M(x1,y1),N(x2,y2),
4+4kx+x??1+k则由①得?7xx=?1+k?1212222 →→,∴OM·ON=x1x2+y1y2
4k?1+k?+8=12 1+k?k=1(经检验符合题意),∴k=1.
课后练习区 1.相交 2.-
33
3.3
解析 =(1+k2)x1x2+k(x1+x2)+1=
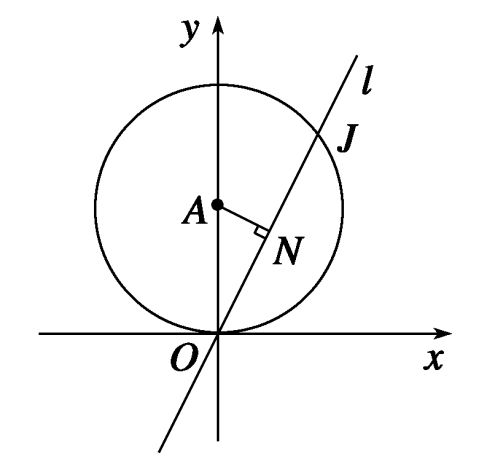
如图所示,
x2+y2-4y=0?x2+(y-2)2=4,
∴A(0,2),OA=2,A到直线l:y3x的距离是AN=1, ∴ON3,∴弦长OJ=3.
4.(4,6) 5.1 6.-10
7.1
|0+0-5|解析 圆C1的圆心C1(0,0)到直线3x+4y-5=0的距离为1,圆C1的半径为3+42,AB弧上的点到直线3x+4y-5=0距离最大为2-1=1,因此圆C2的半径最大为1.
8.-3+22
解析 设∠APB=2θ,则∠APO=∠BPO=θ,
1→→→2PA·PB=(PA)·cos 2θ=cos 2θ tanθ
21-sinθ1=·(1-2sin2θ)=2sin2θ-3≥2-3, sinθsinθ
12当且仅当2sin2θ,即sin2θ= sinθ2
3π9.解 (1)当α=kAB=-1, 4
直线AB的方程为y-2=-(x+1),即x+y-1=0.(3分)
|0+0-1|2故圆心(0,0)到AB的距离d==, 22
从而弦长AB=2 830.(7分) 2
(2)设A(x1,y1),B(x2,y2),
2?x2?1+y1=8,则x1+x2=-2,y1+y2=4.由?22 ?x+y=8,?22
两式相减得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
即-2(x1-x2)+4(y1-y2)=0,
y1-y21∴kAB=分) x1-x22
1∴直线l的方程为y-2=(x+1),
2
即x-2y+5=0.(14分)
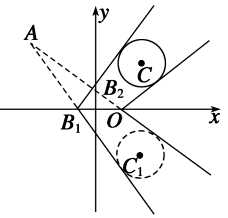
10.
解 已知圆C:x+y-4x-4y+7=0关于x轴对称的圆为C1:(x-2)2+(y+2)2=1,
其圆心C1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切.(4分)
设l的方程为y-3=k(x+3),则 |5k+2+3|1,(10分) 1+k43即12k2+25k+12=0.∴k1=-,k2=-34
则l的方程为4x+3y+3=0或3x+4y-3=0.
(14分)
11.解 两圆的标准方程分别为
(x-1)2+(y-3)2=11,(x-5)2+(y-6)2=61-m,
圆心分别为M(1,3),N(5,6),半径分别为11和61-m.
(1)当两圆外切时,?5-1?+?6-3?=61-m.
解得m=25+1011.(4分) 22
(2)当两圆内切时,因定圆的半径1161-m11=5. 解得m=25-1011.(8分)
(3)两圆的公共弦所在直线的方程为
(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,
即4x+3y-23=0.(12分)
由圆的半径、弦长、弦心距间的关系,不难求得公共弦的长为
?|4+3×3-23|?222×?11?-??=7.(14分) 4+3??
