分 类 号: N941.5 密 级: 学校代码: 10638 学 号: 308070104013

硕 士 学 位 论 文
GM(1,1)模型的优化与一类强化缓冲算子
的构造
姓 名 ******* 指 导 教 师 ******* 教授
培 养 单 位 数学与信息学院 学 科 专 业 应用数学 研 究 方 向 不确定信息系统的预测与决策 申请学位类别 理学硕士 论文提交日期 二○一一年四月 论文答辩日期 二○一一年六月
西华师范大学学位评定委员会
四川·南充
二○一一年六月
Optimization of GM (1, 1) and a Kind of Practical Strengthening Buffer Operator
A Dissertation
Submitted to the Graduate Faculty
In Partial Fulfillment of the Requirement
For the Degree of Master of Natural Science
By
SUN Yan-na
Supervised by
Professor WEI Yong
Major in
Applied Mathematics
In
Department of Mathematics and Information
China West Normal University
Nanchong, Sichuan Province, China
Jun, 2011
目 录
目 录
摘 要........................................................................................................................... II ABSTRACT.................................................................................................................IV
第1章 前言................................................................................................................ 1
1.1 本课题的目的、意义.......................................................................................... 1
1.2 论文的主要内容.................................................................................................. 2
第2章 灰建模及缓冲算子的基础理论 ................................................................... 3
2.1 灰建模的基本原理.............................................................................................. 3
2.2 缓冲算子的基本理论.......................................................................................... 4
第3章 灰色GM(1,1)模型及缓冲算子的研究 ........................................................ 6
3.1 GM(1,1)模型的研究现状.................................................................................... 6
3.2 缓冲算子的研究现状.......................................................................................... 8
第4章 GM(1,1)模型建模方法的改进 ............................................................... 9
4.1 优化灰导数的等间距GM(1,1)........................................................................... 9
4.2 优化灰导数的非等间距GM(1,1)..................................................................... 13
第5章 一类新的缓冲算子的构造及缓冲算子新定理 ......................................... 19
5.1 一类新的实用强化缓冲算子的构造................................................................ 19
5.2 缓冲算子新定理................................................................................................ 22
第6章 结论与展望 ................................................................................................. 25
6.1 全文总结............................................................................................................ 25
6.2 研究展望............................................................................................................ 26
参考文献...................................................................................................................... 27 致 谢.......................................................................................................................... ⅰ 关于学位论文使用授权的声明.................................................................................. ⅱ 关于学位论文原创性的声明...................................................................................... ⅲ 在学期间的科研情况.................................................................................................. ⅳ
I
摘 要
摘 要
GM(1,1)模型是灰色系统预测理论的基础与核心[1],它已被广泛应用于农业、工业、气象、电力、经济、社会等领域。它将系统看成一个随时间变化而变化的指数函数,不需要大量的时间序列数据就能够建立预测模型,其计算简单已被普遍认同。但是一方面灰色系统理论还存在一些缺陷,其模型精度有待进一步提高,很多学者已在提高精度方面做了很多研究[3-7]。另一方面,由于现实生活中的数据往往因受到外界很多冲击因素的干扰而失真,为了排除扰动因素的作用,刘思峰教授开创了对波动数据预测的新领域,他针对级比渐趋稳定的数据序列,提出了用满足缓冲三公理的缓冲算子作用后进行建模预测的新思路,众多学者从不同的背景出发,提出了各种缓冲算子,大大提高了灰色预测建模精度,从而大大拓广了灰色系统理论的应用范围。文献[41]将缓冲算子的构造与函数结合起来,为缓冲算子的构造开辟了新方向,文献[49]对缓冲算子公理进行了补充,并构造了变权缓冲算子。
本选题在他们的工作的基础上,主要研究成果如下:
(1)通过对不用一次累加而直接建模的等间距GM(1,1)模型的灰色微分方程中的灰导数进行优化,提出了用z(t)?A(x(t)?C),(其中A?ln((0)?
?(1)x(0)(k)(1)x(0)(k?1),代))
替原始灰色微分方程中的灰导数,同时用x(0)(k)代替原始灰色微分方程中的背景值z(1)(k),得到新的灰色微分方程z(k)?ax(0)(k)?b,从而获得新模型,经过严格理论验证该模型具有指数,系数,平移常数重合性。大量的数据模拟和模型比较结果表明,优化后的模型提高了背景值的准确性以及灰预测模型的拟合精度和预测精度,且该模型既适合于低增长指数序列建模,也适合于高增长指数序列建模,同时也适合于非齐指数序列建模,可见新的建模方法大大提高了模型的模拟精度与预测精度,同时扩大了模型的适用范围。
(2)基于完全沿用等间距一次累加的原始非等间距模型精度不尽人意,但各种改进非等间距模型一次累加表达式复杂、计算繁琐这一基本事实,依据各种非等间距预测表达式都具有数据预测序列是时序指标的齐次指数函数的共同特征,提出不涉及非等间距的一次累加表达式,更无需其计算值,直接建立非等间距灰色微分方程,同时优化其灰导数,用序列拟合误差平方和最小来寻求最佳初始条件,获得了模拟预测精度较高的非等间距灰色预测模型。
(3)文献[41]将缓冲算子的构造与函数结合起来,为缓冲算子的构造开辟了新方向,文献[49]对缓冲算子公理进行了补充,并构造了变权缓冲算子。本选题在他
II
摘 要
们的工作的基础上,构造了一类缓冲算子,整合了这些常用的缓冲算子,使得常用缓冲算子更一般化了,也更加灵活了。
(4)在现有灰色系统缓冲算子公理体系下,本文得到了以下结果:设D为一强化(或弱化)缓冲算子,X?(x(1),x(2),?,x(n))为系统原始行为数据序列,其缓冲序列为XD?(x(1)d,x(2)d,?x(n)d),f,g均为单调函数,并具有相同的单调性,且满足g(f(x(k)?,k?1,2,?,n,XD1?(x(1)d1,x(2)d1,?x(n)d1),其中))x(k
x(k)1d?g[f(x(k),)则无论d]X为单调增长序列,单调衰减序列还是振荡序列, D1均为强化(或弱化)缓冲算子。
关键词:灰色理论;GM(1,1)模型;模型的改进;缓冲算子
III
Abstract
Abstract
GM (1, 1) is the foundation and core of grey system prediction theory [1-2]. And it has widely applied in numerous fields, such as agriculture, industry, meteorology, electric power, economy, society and so on. It regards a system as the exponential function which changes with the time variation, and does not need the massive time series data to establish the forecast model. The calculating simpleness for GM (1, 1) has been accepted by people. However, on the one hand, there are still some deficiencies in grey system theory, the accuracy of model need to be further improved. Many scholars have done a lot of research in improving the model accuracy [3~7]. On the other hand, due to real-life data tend to be under a lot of the impact of external interference factors, in order to exclude the impact of disturbance factors, Professor Liu Sifeng created a new field in prediction of fluctuated data, he aimed at the data series whose grade radio is becoming more and more stable, and presented a new idea to model for prediction after using the buffer operator based on the 3 axioms ,many scholars started from different backgrounds, and proposed a variety of buffer operators, then greatly increased the accuracy of grey prediction model, thus significantly broadened the field of application of grey system theory. Literature [41] connected the structure of buffer operator with functions, and opened a new direction for the structure of buffer operator .Literature [49] was supplemented for the buffer operator axioms, and constructed a variable weight buffer operator.
In this paper, on the basis of their work, the work in this dissertation mainly consists of following parts:
(1) This paper presents a new method to establish the direct model through optimizing
z(t)?ln(?
?(1)the x(0)(0)grey (k))(x(0)derivative, replacing the derivative (1)x(0)(k) by x(k?1)we getz(k)?ax(0)(k)?b. The new model has been proven strictly to have the property (1)(t)?C), and the background valuez(k) byx(0)(k), then
of exponent, coefficient and translation constants superposition. The results of data simulation and model comparison show that the improved model in this paper raises the accuracy of background value, the fitting precision and forecasting precision. Moreover, it is not only suitable for the low growth sequence, but also suitable for the high growth sequence. What’s more, it is suitable for the nonhomogeneous exponential sequence. The new method not only improves the simulation and prediction precision, but also extends the application scope of GM (1, 1) model.
(2)Based on the truth that the accuracy of the original non-equidistance
IV
Abstract
model ,which completely adherence to 1-Ago of equidistance sequence ,is not satisfactory, but the 1-Ago expressions in the ways to improve the non-equidistance model are very complex and the calculation is very complicated, according to a variety of non-equidistance expressions have the common features that forecast sequence is the homogeneous exponential function about timing indicator, this paper proposes a method to establish gray differential equation of non-equidistant sequence directly, which does not involve the 1-Ago expressions of non-equidistance sequence , even without its calculated value, optimizing its gray derivative, with the sequence of squares and the smallest fitting error to find the best initial conditions, then we obtain a higher prediction accuracy of non-equidistant gray prediction model.
(3) Literature [41] connected the structure of buffer operator with functions, and opened a new direction for the structure of buffer operator .Literature [49] was supplemented for the buffer operator axioms, and constructed a variable weight buffer operator. This paper, on the basis of their work, constructs a class of buffer operator to integrate these common buffer operators, and make the buffer operator is more general and commonly used, and also more flexible.
(4)Based on the present theories of buffer operators in grey system, the following results are obtained in this paper: Assume that Dis a Strengthening (or weakening) Buffer Operator, X?(x(1),x(2),?,x(n)) is a sequence of raw data, XD?(x(1)d,x(2)d,?x(n)d)is a buffer sequence, f,gare all monotonously functions, and have the same monotonicity,satisfying g(f(x(k)))?x(k),k?1,2,?,n,XD1?(x(1)d1,x(2)d1,?x(n)d1),x(k)d1?g[f(x(k))d], then whenever X is a
monotonously increasing sequence, a monotonously decreasing sequence, or a vibration sequence, D1 is a strengthening(or weakening) operator.
Key words: grey system theory; GM (1, 1); improvement of model; buffer operators
V
第1章 前言
第1章 前言
1.1 本课题的目的、意义
由于元素信息不完全,结构信息不完全,边界信息不完全,运行行为信息不完全等造成的信息部不完全构成了我们“灰”的基本含义。在人们的社会经济活动、科研活动以及日常生活中经常会遇到信息不完全的情况,随着科学技术的高速发展,如何更有效地提高筛选和处理信息的能力,已引起人们的高度重视。在对系统行为的研究过程中,由于内在、外在因素的扰动的存在和人们认识事物水平的局限,使得人们所得到的信息以及对许多事物或系统的认识是不完全的,往往带有某种不确定性。随着现代科学技术的不断发展和人类社会的进步,人们对不确定性系统的研究也日益深入,出现了一大批从不同角度、不同侧面描述和处理各类不确定性信息的理论、方法和成果,如模糊数学、灰色系统理论、粗糙集理论、未确知数学等。在自然界和社会科学领域,不确定性问题普遍存在。针对“随机不确定”现象,及服从某种典型分布的对象,可以用概率统计去解决;而对于“认知不确定”问题,及内涵明确,外延不明确的对象,可以用模糊数学去研究。然而,对于另外一类不确定性问题,即少数据、小样本、贫信息的不确定性问题,概率统计、模糊数学就难以解决,灰色系统理论正好解决了这类难题,它的研究对象就是“部分信息已知、部分信息未知”的“小样本”、“ 少数据”、“贫信息”不确定性系统。灰色系统理论通过对“部分” 已知信息的生成和开发来提取有用的信息,并实现对人类现实世界和事物发展趋势的确切描述和认识[1]。
19xx年,我国学者邓聚龙教授的两篇开创性论文“灰色系统的控制问题”和“灰色控制系统”的公开发表,标志着灰色系统理论这一新兴横断学科的问世。这一新理论收到国内外学术界和广大实际工作者的积极关注,许多学者开始以极大的热情开展理论探索及其在不同领域的应用研究工作。该理论在众多科学领域中得到许多成功的应用,赢得了国际学术界的肯定和关注。世界上有100多所大学,国内外有很多出版机构,国际权威行检索机构,许多重要国际会议等都对灰色系统理论给予了肯定,并对世界系统科学界同行进一步了解灰色系统理论起到了积极作用。
经过近30年的发展,灰色系统理论已形成了以“灰”为研究对象,在“差异信息原理”、“解的非唯一性原理”、“最少信息原理”、“认知根据原理”、“新信息优先原理”、“灰性不灭原理”的基础之上,建立起了一门新兴许可的结构体系。它的主要内容包括以灰色代数系统、灰色方程、灰色矩阵等为基础的理论体系,以灰色关联空间为依托的分析体系,以灰色序列生成为基础的方法体系,以灰色模型(GM)为核心的模型体系,以系统分析、评估、建模、预测、决策、控制和优化为主体的技术体系 [1-2]。
1
第1章 前言
灰色模型作为灰色系统理论的模型体系的核心,已被广泛应用于农业、工业、气象、电力、经济、社会等领域,并获得了较为合理的研究结论,掌握了事物发展变化的规律,并为我们预测事物的发展趋势提供了理论依据。GM(1,1)模型是灰色模型的基础与核心,将系统看成一个随时间变化而变化的指数函数,不需要大量的时间序列数据就能够建立预测模型,其计算简单已被普遍认同。但是灰色系统理论还存在一些缺陷,其模型精度有待进一步提高。另外由于现实生活中的数据往往因受到外界很多冲击因素的干扰而失真,为了排除扰动因素的作用,刘思峰教授开创了对波动数据预测的新领域,他提出了用满足缓冲三公理的缓冲算子作用后进行建模预测的新思路。灰色预测模型的应用范围日趋广泛,也成为了我们研究贫信息的不确定系统的重要方法,因而对灰色预测模型及缓冲算子的研究具有较为重要的学术意义和较为广泛的应用价值。
1.2 论文的主要内容
本文共分六章。第一章是前言,介绍了灰色系统的发展状况和研究动态;第二章介绍了灰建模的基本原理和缓冲算子的基本理论;第三章介绍了灰色GM(1,
1)模型的研究现状及缓冲算子的研究现状;第四章通过对原始GM(1,1)模型的研究和分析,分别对等间距和非等间距的GM(1,1)模型作出了改进和优化;第五章通过对现有缓冲算子的分析,构造了一类新的实用强化缓冲算子,并得出了缓冲算子的新定理;最后一章结论主要对前五章的研究成果加以总结,并对未来的研究提出了展望。
2
第2章 灰色建模及缓冲算子的基础理论
第2章 灰建模及缓冲算子的基础理论
2.1 灰建模的建模机理
研究一个系统,一般应先建立系统的数学模型,进而对系统的整体功能、协调功能以及系统各个因素之间的关联关系、因果关系、动态关系进行具体的量化研究。灰预测数据有以下内涵特点:序列性、少数据性、全新息性、时间传递性和灰因白果律。
2.1.1 等间距GM(1,1)模型的建模机理 先介绍两种灰序列生成算子:
累加生成是使灰色过程由灰变白的一种方法,它在灰色系统理论中占有极其重要的地位。
累减生成是在获取增量信息时常用的生成,累减生成对累加生成起还原作用。累减生成与累加生成是一对互逆的序列算子。
设X?0???x?0??1?,x?0??2?,x?0??3??,x?0??n??为原始数据序列,则
x
?0?
k
?k?d1
?
?
i?1
x
?
?0?
?k?称为
x??
0?
X
(0)
的一次累加生成算子(记为1-AGO);
x
?0?
?k?d2
?x
0?
k?
k
?
??1?称为X(0)的一次累减生成算子(记为1-IAGO)
GM(1,1)的灰微分方程模型的基本形式为x(0)(k)?az(1)(k)?b,其中x(0)(k)为
(1)(1)
(k)?x(k?1)))灰导数,a为发展系数,z(1)(k)为白化背景值(z(1)(k)?x,
1
2
?x(0)(2)???z(1)(2)
?(0)??(1)x(3)?z(3)?,??(a,b)T为参数列,B??b为灰作用量。若a且Y????????(0)??(1)?x(n)????z(n)??
1?
?1?,则GM(1,1)???1??
??(BTB)?1BTY. 模型x(0)(k)?az(1)(k)?b的最小二乘估计参数列满足a
2.1.2 非等间距GM(1,1)模型的建模机理
定义1[1] 设序列X
?0?
?x
?
?0?
?k1?,x?0??k2?,x?0??k3??,x?0??kn??,若间距
?0?
?ki?ki?ki?1?const,则称X(0)是非等间距序列。
令x?
0?
为非等间距序列,x?
?
x
??0
?1?k,
??
x?
2
?
k,
??
?x??3
k,
??
x, ?n??
k
?ki?ki?ki?1?const,i?2,3,?,n,则非等间距GM(1,1)定义型为
3
第2章 灰建模及缓冲算子的基础理论
?x
(1)
(ki)
?ki
i
?az
(1)
(ki)?b
)
,其中?x((1ik)?
x
(i
(1
k?)
)
?1
xi(
(
k?)
1)
,ix(k)
x
(1)
(ki)?
?x
m?1
(0)
(km),z
(1)
(ki)?0.5(x
(1)
(ki)?x
(1)
(ki?1))
2.2 缓冲算子的基础理论
定义1[2] 设X?(x(1),x(2),?,x(n))为系统行为数据序列,若 ⑴ 若?k?1,2,?,n?1,x(k)?x(k?1),则称X为单调增长序列; ⑵ 若?k?1,2,?,n?1,x(k)?x(k?1),则称X为单调衰减序列; ⑶ 若?k,k'??1,2,?,n?1?,有x(k)?x(k?1),x(k')?x(k'?1),则称X为振荡序列。令M?max?x(k)k??1,2,?,n??,称M?mm?max?x(k)k??1,2,?,n??,为序列X的振幅。
定义2[2] 设X?(x(1),x(2),?,x(n))为系统行为数据序列,D为作用于X的算子,X经过D作用后记为XD?(x(1)d,x(2)d,?,x(n)d),称D为序列算子,称XD为一阶算子作用序列。
序列算子作用可以多次进行。相应地,若D1,D2,D3都为序列算子,称D1D2为二阶算子作用序列,等等。
公理1[2] (不动点公理)设X为系统行为数据序列,D为序列算子,则D满足x(n)d?x(n)。
公理2[2](信息充分利用公理)系统行为数据序列X中的每一个数据x(k),
k?1,2,?,n都应充分参与算子作用的全过程。
公理3[2](解析化、规范化公理)任意的x(k)d,k?1,2,?,n,都可以由一个统一的x(1),x(2),?,x(n)初等解析式表达。
公理4[49] (单调性不变公理)设X经序列算子D作用后所得数据序列为
XD?(x(1)d,x(2)d,?,x(n)d),则序列XD
与序列X的单调性必须保持一致。
定义3满足以上四公理的序列算子称为缓冲算子,一阶、二阶、三阶……缓冲算子作用序列称为一阶、二阶、三阶……缓冲序列。
定义4[2] 设X为系统行为数据序列,D为缓冲算子,若满足下列两个条件,则称缓冲算子D为强化缓冲算子。
⑴ 当X为单调增长(单调衰减)序列时,缓冲序列XD比系统行为数据序列X的增长率(衰减率)加快;
⑵ 当X为振荡序列时,缓冲序列XD比系统行为数据序列X的振幅大。 定理1[2] 设X?(x(1),x(2),?,x(n))为系统行为数据序列,缓冲序列记为
XD?(x(1)d,x(2)d,?x(n)d),那么
⑴ 当X为单调增长序列时,D为强化缓冲算子?x(k)d?x(k),
4
第2章 灰建模及缓冲算子的基础理论
k?1,2,?,n;
⑵ 当X为单调衰减序列时,D为强化缓冲算子?x(k)d?x(k),k?1,2,?,n;
⑶ 当X为振荡序列时,D为强化缓冲算子则max?x(k)d??max?x(k)?,1?k?n1?k?n1?k?nmin?x(k)d??min?x(k)?。 1?k?n
从上述定理可以看出,单调增长序列在强化算子作用下,数据萎缩;单调衰减序列在强化缓冲算子作用下,数据膨胀。
5
第3章 灰色GM(1,1)模型及缓冲算子的研究
第3章 灰色GM(1,1)模型及缓冲算子的研究
3.1 GM(1,1)模型的研究现状
3.1.1 等间距GM(1,1)模型的研究现状
邓聚龙教授最先提出GM(1,1)的灰微分方程模型的基本形式为x(0)(k)?az(k?)
1(1)(1)(0),其中bx(k)为灰导数,a为发展系数,z(k)为白化背景(1)(1)??(a,b)T为参数列,且值(z(1),b为灰作用量。若a(k)?x(k)?x(k?1)))2
?x(0)(2)???z(1)(2)
?(0)??(1)x(3)?,B???z(3)Y??
??????(0)??(1)?x(n)????z(n)??1??1?(1),则GM(1,1)模型x(0)(k)?az(k)?b的最小二乘???1??
??(BTB)?1BTY.经过众多学者的分析和研究,GM(1,1)建模步骤估计参数列满足a
中存在以下几个问题:
第一,利用灰色微分方程求发展系数a,灰作用量b时,最小二乘法指标函数不一定最合理,不一定是最优的方法,可以寻求更合理的方法来处理参数列??(a,b)Ta。
第二,利用白化微分方程求含a,b的响应式,灰色、白化微分方程本来不统一。
?(1)(1)?x(1)(1)?x(0)(1)求响应式中的待定系数,时间第三 : 利用初始条件x
操之过急, 选择单一。
第四:灰色微分方程中导函数、原函数是近似,可以通过数学方法使得方程中的原函数与导函数更匹配。
根据以上几个问题,很多学者做了研究,改进 GM(1,1)模型的建模方法主要有以下几种:(1)求参数列的方法;(2)改白化微分方程、改灰色微分方程、同时改白化和灰色微分方程、去白化微分方程,通过这些方法来实现灰色、白化微分方程的统一;(3) 对模型的初始条件进行改进; (4)对背景值的改进,优化灰导数,或同时优化这两者,使得方程中的原函数与导函数更匹配。
陈友军等人分析了最小二乘法指标函数的不一定合理性,并提出了用关联度最大作指标函数来求参数列a,b。对微分方程的改进上也有很多学者作了研究,
6
第3章 灰色GM(1,1)模型及缓冲算子的研究
这里主要介绍下(3),(4)两种改进途径的研究现状。
(1)初始条件的改进
通过对模型产生误差的原因分析,有学者认为将x(1)(1)作为初始条件是不合理的,并有不少学者在这方面做了很多研究工作,对模型的初始条件的改进方法主要有以下两类:①根据灰色理论的新信息优先原理,将最后一项即最新的数据x(1)(n)作为灰色微分模型的初始条件[24],在此基础上,另有学者提出了以任一项数据x(1)(m)m?1,2,?,n作为初始条件(即将m从1到n取值,对每一个值用GM(1,1)模型进行一次预测,找出平均相对误差最小(或在其他评价标准下)的模型对应的m,令m对应的x(1)(m)为初始条件)[26],②根据最小二乘法理论,有学者提出用模拟(预测)值与原始数据的误差平方和最小来确定初始条件,通过对模型的初始条件的改进,大大地降低了预测误差。
(2)对背景值的改进
经过不少学者的研究分析,原始灰色GM(1,1)模型中背景值与灰导数不完全匹配,背景值的构造是产生误差的主要原因,因此,不少学者对模型的背景值的改进进行了研究,主要有以下改进方法:①运用指数平滑法将原背景值
[18-26](1)(1)(1)(1),②罗党k?1,2,?,n?1z(k)优化为:Z(k)??x(k)?(1??)x(k?1)
等人做了更进一步的改进,对一阶线性微分方程两边进行积分,将原背景值z(1)(k)优化为:z(k)=(1)x
lnx(1)(1)(k)?x(1)(k?1)(1)(k)?lnx(k?1) k?2,3,?n[3]。通过对模型背景
值的改进,使得新模型不仅适用于低增长序列同时适用于高增长序列,而且模拟精度也大大提高了。
(3)对灰导数的改进
GM(1,1)模型的灰微分方程的基本形式是x(0)(k)?az(1)(k)?b
是邓聚龙教授在白化微分方程dx(1)k?2,3,...,(1)
dt?ax
(1)(1)将离散点列x?b的基础上,
(1)(1)(0)在k点的导数用差分形式来处理(即:
x(1)dxdt?xt?k(k)?x(k?1)?x(k)),将背景值(k)用z(1)(k)来代替而得到的。然而,这样的近似处理,使得GM(1,1)模型的模拟误差较大,因此,很多学者对灰导数进行了研究和优化:
文献[5] 不用一次累加而直接建模,并提出了以向前差商和向后差商的优化加权平均值作为灰导数白化值建立GM (1, 1) 的方法,并证明了该法具有线性变换一致性。
7
第3章 灰色GM(1,1)模型及缓冲算子的研究
3.1.2 非等间距GM(1,1)模型的研究现状
GM (1 ,1) 模型模拟和预测精度主要取决于参数a 和b ,而参数a 和b 的值又依赖于背景值的构造,因此,背景值成为直接影响GM(1 ,1) 模型模拟和预测精度的关键,而一次累加的定义直接影响背景值的构造。学者对非等间距GM (1 ,1) 模型的研究主要是对序列一次累加的定义的改进:
(1)在文献[38]中累加定义给出x?ki??
x?1??1??x?kj??kj,实际上这里的?0?j?1i?ki?可以理解为是将非等间距插值(以便利用等间距思路来处理非等间距问
题),但它在插值的时候没有考虑值的逐渐变化,而是采用了值的突变,这样就给模型带来了一定的误差,也在一定程度上影响了灰色系统理论的应用。
(2)文献[38]中的x???ki?可以理解为是将非等间距插值(以便利用等间距1
思路来处理非等间距问题),但由于它在插值的时候没有考虑值的逐渐变化,而是采用了值的突变,这样就给模型带来了一定的误差,也在一定程度上影响了灰色系统理论的应用,文献[27]通过考虑值的逐渐变化来给出新的累加定义:
x?1??ki??x?0?i
j?1?kj?k1???{?[xl?1?0??kj?1??x(0)(kj)?x?kj(0)(kj?1)l]}
(3)当原始数据经过一次累加后,如果还不接近指数形式,我们应当进行数据处理,使其接近指数形式,这样才可能得到好的模拟效果,又因为我们用指数形式进行模拟,文献[28]提出用x???t??ce对原始数据进行插值,得到了新的0dit
i
一次累加定义x?ki???1?x?0?i?kj?k1????cj?1e
j?2l?1dj?1?kj?1?l??
3.2 缓冲算子的研究现状
由于现实生活中的数据往往因受到外界很多冲击因素的干扰而失真,为了排除扰动因素的作用,刘思峰教授开创了对波动数据预测的新领域,他针对级比渐趋稳定的数据序列,提出了用满足缓冲三公理的缓冲算子作用后进行建模预测的新思路,众多学者从不同的背景出发,提出了各种缓冲算子,大大提高了灰色预测建模精度,从而大大拓广了灰色系统理论的应用范围。文献[43]将缓冲算子的构造与函数结合起来,为缓冲算子的构造开辟了新方向,文献[49]对缓冲算子公理进行了补充,并构造了变权缓冲算子。本文在他们的工作的基础上,构造了一类缓冲算子,整合了这些常用的缓冲算子,使得常用缓冲算子更一般化了,也更加灵活了。
8
第4章 GM(1,1)模型建模方法的改进
第4章 GM(1,1)模型建模方法的改进
在本章里,作者对GM(1,1)模型进行了深入研究,根据GM(1,1)模型的原理,找出影响模型精度及其适应性的关键因素,并对其进行优化,提高了模型的精度,扩大了模型的适用范围,实例表明新模型具有较满意的模拟和预测效果,具有重要的理论价值和实际价值。
4.1优化灰导数的等间距GM(1,1)
虽然文献[3]、[4]、[7]从优化背景值的角度进行改进,使得白化微分方程与灰色微分方程更加匹配,大大提高了模型的精度,文献[5]不用一次累加而直接建模,并提出了以向前差商和向后差商的优化加权平均值作为灰导数白化值建立GM (1, 1) 的方法,但是根据GM(1,1)模型的原理,它将系统看成一个随时间变化而变化的指数函数,本文通过对不用一次累加而直接建模的灰色微分方程中的灰导数进行优化,从而优化了GM(1 ,1) 模型,数据模拟和模型比较表明,与原GM (1,1) 模型和文献[7]中提出的优化模型相比,本文优化后的模型模拟精度有所提高,具有较高的理论价值和应用价值。
4.1.1 对灰导数的优化
定理 1 设原始数据序列x?0???x?0??1?,x?0??2?,x?0??3??,x?0??n??,x?0?的1-IAGO序
00?10?)列为?(1x)?????(x?2?,??x?(?1)?3?,?,??x?0(1)??n,若x?0?满足指数形式
x?0?(k)=BeA(k?1)+C,则x?0?与?(1)x?0?具有相同的指数。
证明:若x?0?满足指数形式x?0?(k)=BeA(k?1)+C,则
?(1)x?0?(k)=x?0?(k)?x?0?(k?1)=BeA(k?1)+C?(BeA(k?2)+C)
=B(1?e?A)eA(k?1)
令D?B(1?e?A),则?(1)x?0?(k)=DeA(k?1)
若?(1)x?0?(k)满足齐次指数形式?(1)x?0?(k)=DeA(k?1),
x?0?k
(k)=??
i?2(1)x?0?(i)?x(0)(1)=B(1?e?A)(eA?e2A???e(k?1)A)?x(0)(1)
=BeA(k?1)+C,
即x?0?与?(1)x?0?具有相同的指数。证毕!
上述定理说明离散指数函数与其经一次累减生成的离散指数函数具有相同的指数。根据GM(1,1)模型的原理,它将系统看成一个随时间变化而变化的
9
第4章 GM(1,1)模型建模方法的改进
指数函数,
定理2 设原始数据序列x?0???x?0??1?,x?0??2?,x?0??3??,x?0??n??, 则
1)若x满足非齐次指数形式,即x
dx(?0??0?(k)=BeA(k?1)+C,则A?ln(??)1)0(()1)0((x(k)(k?1)x),k?3。令(k)0)z(t)?dx((t)0)dt
)?A(x((t)?C)0),写成离散形式有z(k)?dk
?0??A(x((k)?C); 02)若x近似满足指数形式,即x(k)?Be
dx?0?A(k?1)+C,令Ak?ln(??1()(0)x(k)(k?1)1()(0)x),k?3。令z(t)?(0)dx((t)0)dt?At(x((t)?C)0),写成离散形式有
z(k)?(k)
dk?Ak(x(0)(k)?C)。
4.1.2利用优化的灰导数建模 灰色微分方程为
z(k)?ax(0)(k)?b (1)
将z(k)?A(x(0)(k)?C)代入(1),有
A(x(0)(k)?C)?ax(0)(k)?b
整理得,
Ax(0)(k)?ax(0)(k)?b?AC
记b?AC?b?,Ax(0)(k)?z?(k),则有
z?(k)?ax
?(0)(k)?b? (2) (2)式的最小二乘估计参数序列为a??(a,b?)T?(BTB)?1BTY,其中,
??x(3)?z?(3)?????(0)z(4)?x(4)??,B?Y??????????(0)?z(n)?????x(n)(0)1??(0)(0)?a1?x(2)?x(1)e。令C?,则b?b??AC,由?a1?e???1??
??(a,b)T。 此可得①式的最小二乘估计参数序列为a
1) 白化微分方程
dx(0)(t)dt?ax(0)(t)?b的时间响应函数为 10
第4章 GM(1,1)模型建模方法的改进
?0?x?t??b??a(t?1)b??0?x1?e?????a?a?
2) 灰色微分方程z(k)?ax(0)(k)?b的时间响应式为
x?0??k??b??a(k?1)b??0?x1?e?????a?a?, k?1,?n
定理 3 当原始序列为x?0?(k)=BeA(k?1)?C严格满足指数函数形式的时候,由新灰色微分方程z(k)?ax(0)(k)?b,其中z(k)?A(x(0)(k)?C), 和白化微分方程dx(0)(t)
dt?ax(0)(t)?b(其中a,b如2.2所述),组成的新GM(1,1)模型得到的模拟?(0)的指数,系数,平移常数与x?0?具有重合性。 序列x
证明:设原始序列为x(0)(k)?BeA(k?1)?C,则z(k)?A(x(0)(k)?C),则存在常数a??A和b??AC,使灰色微分方程z(k)?ax(0)(k)?b成立。因此
b??a(k?1)b??0??AC??A(k?1)??AC?A(k?1)?(0)(k)?x???1??xe??B?C?e??Be?C????????a?a????A????A?
即当原始序列x?0?满足指数函数形式的时候,新GM(1,1)模型得到的模拟序列?(0)(k)的指数,系数,平移常数与x(0)(k)的指数,系数,平移常数具有重合性。x
证毕!
4.1.3数据模拟与精度比较
例1 以标准指数列x(0)(k?1)?e?ak取不同的发展系数a生成不同原始数据,我们分别以文献[4]的模型M1、文献[7]的M2和本文的新GM(1,1)模型M3进行数据拟合并比较其精度。
我
xi(们)分(别0)取?ai?0.1,0.2,0.4,0.6,0.8,1.0,1.5,2.0,2.5,3.0,得?{0xi(?1)xi, ,k?0,,?,5可得6)1,以表}1的数据为原始数据,用本文新
的GM(1,1)模型建模,并求出其平均绝对误差和平均相对误差。并与文献[7]的结论进行比较,得出表2
由表2可以看出无论是从模型平均相对误差还是平均绝对误差来看,本文的新GM(1,1)都大大优于其他模型。其实根本没有模型误差,只有因近似计算带来的计算误差。
表1: 原始数据
11
第4章 GM(1,1)模型建模方法的改进
xi
(0)
i
?ai
(1)
xi
(0)
(2)
xi
(0)
(3)
xi
(0)
(4)
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.1052 1.2214 1.4918 1.8821 2.2255 2.7183
1.2214 1.4918 2.2255 3.3201 4.9530 7.3890
1.3499 1.8221 3.3201 6.0496 11.0232 20.0855 90.0171 403.4288
xi
(0)
(5)
xi
(0)
(6)
1 2 3 4 5 6 7 8 9 10
0.1 0.2 0.4 0.6 0.8 1.0 1.5 2.0 2.5 3.0
1.4918 2.2255 4.9530 11.0232 24.5325 54.5982 403.4288
1.6487 2.7183 7.3890 20.0855 54.5982 148.4132 1808.0424 268337.2865
4.4817 20.0886 7.3891 54.5982 12.1825 20.0856
2980.9580 22026.4658
148.4132 1808.0424 22026.4658
403.4288 8103.0839 162754.7914 3269017.372
表2 : 三种优化GM(1,1)模型的模拟误差
发展系数
?ai
M1 M2 M3
平均相对平均绝对平均相对误差(%) 误差 0.00187176 2.7756e-16 0.00092811 4.9960e-16 0.00075593 6.6613e-16 0.83996684 4.6074e-15 0.00059526 1.7986e-14 0.00034762 3.0642e-14 0.00383656 5.7732e-13 0.00014417 8.4308e-12 0.00001608 1.0973e-10 0.00006632 1.2251e-9
误差(%) 1.9112e-14 2.2971e-14 1.0493e-14 3.9083e-14 6.1841e-14 4.2231e-14 8.2333e-14 1.0857e-13 1.1680e-13 1.2004e-13
平均绝对平均相对平均绝对误差 0.000032 0.000062 0.000066 0.000166 0.000135 0.000104 0.007874 0.925802 0.809833 18.504937
误差(%) 误差 0.0023 0.0031 0.0013 0.0025 0.0010 0.0004 0.0017 0.0185 0.0014 0.0027
0.0000267 0.0000188 0.0000306 0.0758480 0.0000861 0.0000431 0.0069359 0.0019024 0.0014754 0.432216
0.1 0.2 0.4 0.6 0.8 1.0 1.5 2.0 2.5 3.0
(注:M1, M2模型误差来自文献[7]) 例
x
?0?
2 : 原始数据序列
?{ 2.7180,7.3883,20.0835,54.5925,148.3978,403.3870,1096.5} .这是一个高增
长的序列,我们分别以文献[4]的模型M1、文献[7]的M2和本文的新GM(1,1)模型M3进行数据拟合并比较其精度。以前5个数据为原始数据进行模拟,以后2个数据作为预测效果检验,用本文新的GM(1,1)模型建模,并求出其相对误差。并与文献[7]的结论进行比较,得出表3,以原始数据建立模型可得
a??1.0000
, b? 5.8141e-006,
12
第4章 GM(1,1)模型建模方法的改进
?(0)(k)?{2.7180,7.3883,20.0835,54.5926,148.3981,403.3878,1096.5} x
表3 模拟和预测精度表
模拟值
?(0)(3) x?(0)(4) x?(0)(5) x
M1 相对误差(%)
0.112 -0.522 -1.160 0.506 M1
M2 相对误差(%) 0.00167516061 0.00247850403 0.00255535349 0.002645211916
M2
模拟值
(%)
(%)
403.42334621
-0.001649
403.3878 1096.5
-1.835 -2.484
相对误差
模拟值
M3 相对误差(%) -0.0000417 0.0001838 0.0001910 0.00013882
M3 相对误差(%) -0.00019832
平均误差 (%)
模拟值
模拟值 410.834 1123.837
相对误差
?(0)(6) x?(0)(7) x
1096.5988648 -0.0001035
0.000876
平均误差(%)
2.1595 -0.000099160
(注:M1为文献[4]建立的模型,M2为文献[7]建立的模型,M3为本文的新模型)
由表3可以看出本文的新GM (1,1)模型保持了较高的精度。相比而言,本文的新GM(1,1)模型无论是从模拟精度还是预测精度来看,都比文献[7]高, 其模拟及预测精度几乎达到100%.
4.1.4 总结
本文通过对GM(1,1)模型的灰导数进行优化分析,提出了通过优化灰导数的一种直接建模法,得出新的GM(1,1)模型。经过严格理论验证该模型具有指数,系数,平移常数重合性,而且经过标准指数序列和非标准指数序列的数据的模拟、预测验证,优化后的模型提高了灰微分方程和白化微分方程的吻合性以及灰预测模型的拟合精度和预测精度,并在保持原GM(1,1)模型计算简单等优点的基础上,拓广了其适应范围,该模型既适合用于低增长指数序列建模,也适合用于高增长指数序列建模,同时也适合于非齐指数序列建模!因此具有较高的理论价值和应用价值。
13
第4章 GM(1,1)模型建模方法的改进
4.2优化灰导数的非等间距GM(1,1)
文献[22,34,35]通过将序列的间距作为乘子而生成原始数据序列的一次累加序列,改进了非等间距GM(1 ,1)模型预测模型;文献[38]通过对一次累加生成序列开m次方,用背景值取代中心值,得到了一类基于中心逼近化的非等间距GM(1 ,1)模型预测模型。文献[39,40]提出了非等间距GM (1 ,1) 模型的背景值的改进方法,用齐次(非齐次)指数函数来拟合一次累加生成序列,提出了一种背景值构造的方法,获得了较高的预测精度。但各种改进非等间距模型一次累加表达式复杂、计算繁琐,本文依据各种非等间距预测表达式都具有数据预测序列是时序指标的齐次指数函数的共同特征,提出不涉及非等间距的一次累加表达式,更无需其计算值,直接建立非等间距灰色微分方程,同时优化其灰导数,用序列拟合误差平方和最小来寻求最佳初始条件,获得了模拟预测精度较高的非等间距灰色预测模型,并应用实例表明本文提出方法的有效性。
4.2.1对灰导数的优化
定义1[1] 设序列X?0???x?0??k1?,x?0??k2?,x?0??k3??,x?0??kn??,若间距
(0)?ki?ki?ki?1?con,则称sX是非等间距序列。
由于原始数据序列是接近指数形式的非等间距序列,设x?0?(t)=BeA(t?1),曲线过两点(ki?1,x(0)(ki?1)),(ki,x(0)(ki)),则有:
x
(0)
(ki?1)?Be
A(ki?1?1)
(1),x(0)(ki)?BeA(k?1)(2)
i
由(2)/(1)得
A?
1(ki-ki-1)
ln
xx
(0)
(ki)
(0)
(ki?1)
定理1设原始数据序列X?0???x?0??k1?,x?0??k2?,x?0??k3??,x?0??kn??, 则 1)若x满足齐次指数形式,即x
dx
(0)
?0??0?
(ki)?Be
A(ki?1)
,则A?
1(ki-ki-1)dx
(0)
ln
xx
(0)
(ki)
(0)
(ki?1)
(0)
,
i?2
。令z(t)?
?0?
(t)
dt
?Ax
(0)
(t),写成离散形式有z(ki)?
(ki)
dki1(ki-ki-1)dx
(0)
?Ax
(ki);
2)若x近似满足指数形式,即x(ki)?Be
。令z(t)?
?0?
A(ki?1)
,令Ak?
i
ln
xx
(0)
(ki)
(0)
(ki?1)
(0)
,
i?2
dx
(0)
(t)
dt
?Atx
(0)
(t),写成离散形式有z(ki)?
14
(ki)
dki
?Akix
(ki)。
第4章 GM(1,1)模型建模方法的改进
4.2.2初始条件的确定 白化微分方程
dx
(0)
(t)
dt
?ax
(0)
(t)?b的连续解为:x
(0)
(t)??
ca
e
?at
?
ba
(其中c
为待定系数)。为了达到最佳的拟合效果,根据原值序列拟合误差平方和
n
S?
?[x
i?1
?(0)
(ki)?x
(0)
(ki)]
2
最小来确定最佳系数c:
dSdc
n
显然S是关于c的函数,为求S最小时的c值,令?0即可。
n
2?[?
i?1
ca
e
?ak
i
?
ba
?x
(0)
(ki)](?
e
?aki
a
)?0可得c?
?[b?ax
i?1
ni?1
(0)
(ki)]e
?aki
?e
?2aki
4.2.3利用优化的灰导数建模 灰色微分方程为
z(k)?ax
(0)
(k)?b
?(a,b)
①
T
①式的最小二乘估计参数序列为a
?
?(BB)
(0)
T?1
BY
T
,其中,
??x(k2)?z(k2)?
???(0)
z(k3)?x(k3)??,B?Y??
????????(0)
z(k)?n????x(kn)1?
?1?。 ???1??
1) 白化微分方程
dx
(0)
(t)
dt
?ax
(0)
(t)?b的时间响应函数为
n
x
(0)
(t)??
ca
e
?at
?
ba
?[b?ax
??
i?1
ni?1
(0)
(ki)]e
?aki
e
?2aki
?at
?
ba
a?e
2) 灰色微分方程z(k)?ax
(0)
(k)?b的时间响应式为
n
x
(0)
(ki)??
ca
e
?aki
?
ba
?[b?ax
??
i?1
ni?1
(0)
(ki)]e
?aki
e
?2aki
?aki
?
ba
,k?1,2?n,
a?e
i
定理 2 当原始序列为x?0?(ki)?BeA(k?1)严格满足指数函数形式的时候,由新灰色微分方程z(ki)?ax(0)(ki)?b,其中z(ki)?Ax(0)(ki), 和白化微分方程
15
第4章 GM(1,1)模型建模方法的改进
dx
(0)
(t)
dt
x
?0?
?ax
(0)
?(0)的指数,系数与(t)?b,组成的新GM(1,1)模型得到的模拟序列x
具有重合性。
i
证明:设原始序列为x?0?(ki)?BeA(k?1),则z(ki)?Ax(0)(ki),则存在常数a??A和
b?0,使灰色微分方程z(ki)?ax
n
?(0)
(0)
(ki)?b成立。因此
n
?[b?ax
(ki)??
i?1
ni?1
n
(0)
(ki)]e
?aki
xe
?2aki
?aki
?
ba
?ABe
?
i?1
ni?1
A(ki?1)
e
Aki
e
2Aki
Aki
a?eA?e
?Be
Aki
?e
i?1ni?1
2Aki?A
?Be
2Aki
Aki
e
?A
?Be
A(ki?1)
?e
即当原始序列x?0?满足指数函数形式的时候,新GM(1,1)模型得到的模拟序列
?(0)(k)的指数,系数与x(0)(k)的指数,系数具有重合性。证毕! x
4.2.4数据模拟与精度比较
例1[2] 表1:原始数据表

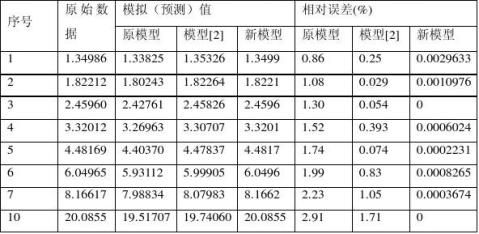
本例以原始的非等间距GM(1,1)模型为原模型,以文献[2]的模型为模型,记本文模型为新模型,得表2:
表2:模型的模拟效果和相对误差表
16
第4章 GM(1,1)模型建模方法的改进
了精度。
例2 [25] P.G 福雷斯研究了许多材料的长寿命对称循环下温度对疲劳强度的影响。表3是钛合金疲劳强度随温度变化的实验数据,这是一个非等间距序列。本文应用文献[25]的数据,用本文提出的方法对其建立模型并进行精度比较得表4。
表3 钛合金疲劳强度随温度变化关系
T/ ℃( ??1(x
ki
)
100 130 170 210 240 270 310 340 380
(0)
(ki))
560 557.54 536.10 516.10 505.60 486.10 467.40 453.80 436.4
表4:模型的模拟效果和相对误差表
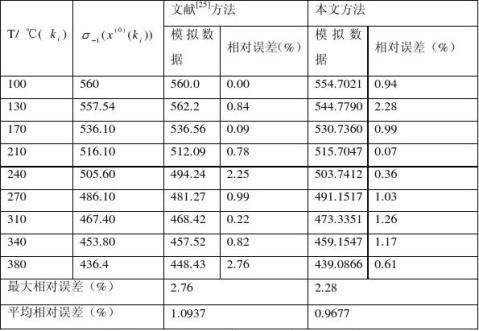
要优于文献[11]的模型,而且本文简化了模型的表达式。 4.2.5总结
本文依据各种非等间距预测表达式都具有数据预测序列是时序指标的齐次指数函数的共同特征,提出不涉及非等间距的一次累加表达式,更无需其计算值,直接建立非等间距灰色微分方程,同时优化其灰导数,用序列拟合误差平方和最小来寻求最佳初始条件,获得了模拟预测精度较高的非等间距灰色预测模型。经
17

第4章 GM(1,1)模型建模方法的改进
过严格理论验证该模型具有指数,系数重合性,而且经过标准指数序列和非标准指数序列的数据的模拟、预测验证,优化后的模型提高了灰微分方程和白化微分方程的吻合性以及灰预测模型的拟合精度和预测精度。不用一次累加而直接用原始数据建模,既简化了计算,又提高了精度,具有较高的理论价值和应用价值。
18
第4章 GM(1,1)模型建模方法的改进
19
第5章 一类新的缓冲算子的构造及缓冲算子新定理
第5章 一类新的缓冲算子的构造及缓冲算子新定理
5.1 一类新的实用强化缓冲算子的构造
由于现实生活中的数据往往因受到外界很多冲击因素的干扰而失真,为了排除扰动因素的作用,刘思峰教授开创了对波动数据预测的新领域,他提出了用满足缓冲三公理的缓冲算子作用后进行建模预测的新思路,众多学者从不同的背景出发,提出了各种缓冲算子,大大提高了灰色预测建模精度,从而大大拓广了灰色系统理论的应用范围。文献[41]将缓冲算子的构造与函数结合起来,为缓冲算子的构造开辟了新方向,文献[49]对缓冲算子公理进行了补充,并构造了变权缓冲算子。本文在他们的工作的基础上,构造了一类缓冲算子,整合了这些常用的缓冲算子,使得常用缓冲算子更一般化了,也更加灵活了。 5.1.1一类新的缓冲算子的构造
定理5.1.1 设 X?(x(1),x(2),?,x(n))为系统原始行为数据序列,x(k)?0,
k?1,2,?,n
,其缓冲序列为X1D?(
r
(x11)d,x?1(2d)
,xn),其(d中
)
x(k)d1?h[wk(x(k),x(k?1),?x(n))g(x(k)),
wn(x(n))?1,wk,g,h
r?0,wk?0,g?0,h?0,
且
均为单调函数,并具有相同的单调性,且满足
为单调增长序列,单调衰减序列还是振
h(g(x(k)))?x(k),k?1,2,?,n则无论X
荡序列,D1均为强化缓冲算子。
证明:D1显然满足缓冲算子四公理,故D1为缓冲算子。 设wk,g,h均为单调递增函数,
(1)当X为单调增长序列时,则0?x(k)???x(i)???x(n) ,因为wk?0,g?0,wk,g为单调递增函数,所以
0?wk???wi???wn?1, 0?gk???gi???gn
因为r?0所以
0?wk???wi???wn?1,
r
r
r
从而
20
第5章 一类新的缓冲算子的构造及缓冲算子新定理
0?wkgk?gk r
因为h?0,h为单调递增函数,所以
0?x(k)d1?h(wkgk)?h(gk)?x(k),即D1对单调增长序列为强化缓冲算子。 r
(2)当X为单调衰减序列,则x(k)???x(i)???x(n)?0,因为wk?0,g?0,wk,g为单调递增函数,所以
wk???wi???wn?1gk???gi???gn?0,
因为r?0所以
wk???wi???wn?1, rrr
从而
wkgk?gk r
因为h?0,h为单调递增函数,所以
x(k)d1?h(wkgk)?h(gk)?x(k),即D1对单调增长序列为强化缓冲算子。 r
(3)当X为振荡序列时,设
x(?)?max?x(k)k?1,2,?,n?,
x(?)?min?x(k)k?1,2,?n?,
因为wk?0,g?0,wk,g为单调递增函数,所以
w??1,w??1,
因为r?0所以
w??1,w??1, rr
从而
w?g??g?,w?g??g?, rr
因为h?0,h为单调递增函数,所以
x(?)d1?h(w?g??h(gk)?x(?),x(?)d1?h(w?g??h(g?)?x(?) rr即D1对振荡序列为强化缓冲算子。
同理可证,当wk,g,h均为单调递减函数时,无论X为单调增长序列,单调衰减序列还是振荡序列,D1均为强化缓冲算子。
5.1.2 应用
21
第5章 一类新的缓冲算子的构造及缓冲算子新定理
定理5.1.2
r
取定理5.1.1中的
h(x)?g(x)?x
,即
x(k)d2?wk(x(k),x(k?1),?x(n))x(k))
k?1,2,?,n则当wk
,
r?0,wk?0,
且
wn(x(n))?1,
为单调递增函数时,无论X为单调增长序列,单调衰减序列
还是振荡序列,D1均为强化缓冲算子。
定理5.1.3 当取定理5.1.2中的wk(x(k),?,x(n))?递增函数时,x(k)d3?
f(x(k))f(x(n))
f(x(k))f(x(n))
,r?1,则f(x)为单调
x(k)是强化缓冲算子。
f(x(k))f(x(n))
定理5.1.4 当取定理5.1.1中的wk(x(k),?,x(n))?
,r?1,g(x)?f(x)h(x)f(x(k))f(x(n))
取作f(x)的反函数,f(x)为严格单调函数,即x(k)d4?h(缓冲算子,这便是文献[41]中的定理2. 定理5.1.5当取定理5.1.1中的
wk(x(k),?,x(n))?r?1,g(x)?f(x),
f(x))是强化
f(x(k))???f(x(n))(n?k?1)f(x(n))
,
h(x)
取
作f(x)的反函数,f(x)为严格单调函数,则X为单调增长序列或单调衰减序列时,x(k)d5?h(中的定理3.
推论5.1.1当定理5.1.3中的f(x(k))?x(k)时
x(k)d6?
x(k)x(n)
?x(k)是强化缓冲算子,这便是文献[47]中的定理4. f(x(k))???f(x(n))(n?k?1)f(x(n))
f(x(k)))是强化缓冲算子,这便是文献[41]
推论5.1.2当取定理5.1.1中的
wk(x(k),?,x(n))?
x(k)???x(n)(n?k?1)x(n)
则X为单调增长序列,r?1,h(x)?g(x)?x时,
是强化缓冲算子,这便是文献?x(k),
或单调衰减序列时x(k)d7?[47]中的定理5. 推
论
5.1.3
x(k)???x(n)(n?k?1)x(n)
取
(x(k))
定
,
理5.1.2中,
的则
wk(x(k),?,x(n))?
?(x(n))?(1??)x(k)
r?1,0???1
22
第5章 一类新的缓冲算子的构造及缓冲算子新定理
(x(k))x(k)d8??(x(n))?(1??)x(k)这便是文献[49]中的定理4. ?x(k)是强化缓冲算子。
5.1.3 结 语
本文将缓冲算子的构造与函数联系起来,构造了一类新的实用强化缓冲算子。由于只要求函数为单调(递增或递减)而非严格单调函数,这样的函数随手可得,一次可以构造一大类缓冲算子,为解决扰动数据序列的建模提供了很多选择,有一定的实用价值。
5.2 缓冲算子新定理
定理5.2.1设D为一强化缓冲算子,X?(x(1),x(2),?,x(n))为系统原始行为数据序列,其缓冲序列为XD?(x(1)d,x(2)d,?x(n)d),f,g均为单调函数,并具有相同的单调性,且满足g(f(x(k)))?x(k),k?1,2,?,n,XD1?(x(1)d1,x(2)d1,?x(n)d1),其中x(k)d1?g[f(x(k))d],则无论X为单调增长序
列,单调衰减序列还是振荡序列, D1均为强化缓冲算子。
证明:D1显然满足缓冲算子公理2和公理3。
设f,g 均为单调递增函数,
(1)当X为单调增长序列时,则x(k)???x(i)???x(n)
因为f为单调递增函数,所以
f(x(k))???f(x(i))???f(x(n)),
因为D为一强化缓冲算子,所以
f(x(k))d???f(x(i))d???f(x(n))d,
f(x(k))d?f(x(k)),k?1,2?n且f(x(n))d?f(x(n))
因为g为单调递增函数,所以
g[f(x(k))d]???g[f(x(i))d]???g[f(x(n))d](公理4),
g[f(x(k))d]?g[f(x(k))],k?1,2?n且g[f(x(n))d]?g[f(x(n))]
即g[f(x(k))d]?x(k),k?1,2?n且g[f(x(n))d]?x(n)(公理1)
故D1对单调增长序列为强化缓冲算子。
(2)当X为单调衰减序列,则x(k)???x(i)???x(n),
因为f为单调递增函数,所以
23
第5章 一类新的缓冲算子的构造及缓冲算子新定理
f(x(k)???f(x(i))???f(x(n)),
因为D为一强化缓冲算子,所以
f(x(k))d???f(x(i))d???f(x(n))d,
f(x(k))d?f(x(k)),k?1,2?n且f(x(n))d?f(x(n))
因为g为单调递增函数,所以
g[f(x(k))d]???g[f(x(i))d]???g[f(x(n))d](公理4),
g[f(x(k))d]?g[f(x(k))],k?1,2?n且g[f(x(n))d]?g[f(x(n))] 即g[f(x(k))d]?x(k),k?1,2?n且g[f(x(n))d]?x(n)(公理1) 故D1对单调衰减序列为强化缓冲算子。
(3)当X为振荡序列时,设
x(?)?max?x(k)k?1,2,?,n?, x(?)?min?x(k)k?1,2,?n?, 同理于(1),(2)的证明,D1满足公理1和公理4,故D1为缓冲算子。
因为f为单调递增函数,所以f(x(k)),k?1,2?n也为振荡序列,且
f(x(?))?max?f(x(k))k?1,2,?,n?, f(x(?))?min?f(x(k))k?1,2,?n? 因为D为一强化缓冲算子,所以
f(x(?))d?f(x(?)),f(x(?))d?f(x(?))
因为g为单调递增函数,所以
g[f(x(?))d]?g[f(x(?))],g[f(x(?))d]?g[f(x(?))]
即g[f(x(?))d]?x(?),g[f(x(?))d]?x(?)
故D1对振荡序列为强化缓冲算子。
同理可证,当f,g均为单调递减函数时,无论X为单调增长序列,单调衰减序列还是振荡序列,D1均为强化缓冲算子。
定理5.2.2 设D为一弱化缓冲算子,X?(x(1),x(2),?,x(n))为系统原始行为数据序列,其缓冲序列为XD?(x(1)d,x(2)d,?x(n)d),f,g均为单调函数,并具有相同的单调性,且满足g(f(x(k)))?x(k),k?1,2,?,n,XD2?(x(1)d2,x(2)d2,?x(n)d2),其中x(k)d2?g[f(x(k))d]则无论X为单调增长序
列,单调衰减序列还是振荡序列, D2均为弱化缓冲算子。
24
第5章 一类新的缓冲算子的构造及缓冲算子新定理
上述性质的证明过程与性质1的证明类似, 略。
作者将缓冲算子的构造与函数联系起来,构造了一类新的实用缓冲算子。由于只要求函数为单调(递增或递减),这样的函数随手可得,已有的任何一个缓冲算子(无论强化还是弱化)都可以得到一大类缓冲算子,为解决扰动数据序列的建模提供了很多选择,有一定的实用价值。
25
第6章 结论与展望
第6章 结论与展望
6.1 全文总结
本选题研究的对象是GM(1,1)预测和缓冲算子的构造。通过对GM(1,1)模型的优化,拓广其应用范围,同时提高了精度。通过分析现有缓冲算子的不足,构建一类强化缓冲算子,扩大了此类强化缓冲算子的范围,并研究了缓冲算子的新定理,为冲击扰动序列建模的数据处理提供了更多的选择。
主要做了以下工作:
(1)通过对不用一次累加而直接建模的等间距GM(1,1)模型的灰色微分方程中的灰导数进行优化,提出了用z(t)?A(x(t)?C),(其中A?ln((0)?
?(1)x(0)(k)(1)x(0)(k?1),代))
替原始灰色微分方程中的灰导数,同时用x(0)(k)代替原始灰色微分方程中的背景值z(1)(k),得到新的灰色微分方程z(k)?ax(0)(k)?b,从而获得新模型,经过严格理论验证该模型具有指数,系数,平移常数重合性。大量的数据模拟和模型比较结果表明,优化后的模型提高了背景值的准确性以及灰预测模型的拟合精度和预测精度,且该模型既适合于低增长指数序列建模,也适合于高增长指数序列建模,同时也适合于非齐指数序列建模,可见新的建模方法大大提高了模型的模拟精度与预测精度,同时扩大了模型的适用范围。
(2)基于完全沿用等间距一次累加的原始非等间距模型精度不尽人意,但各种改进非等间距模型一次累加表达式复杂、计算繁琐这一基本事实,依据各种非等间距预测表达式都具有数据预测序列是时序指标的齐次指数函数的共同特征,提出不涉及非等间距的一次累加表达式,更无需其计算值,直接建立非等间距灰色微分方程,同时优化其灰导数,用序列拟合误差平方和最小来寻求最佳初始条件,获得了模拟预测精度较高的非等间距灰色预测模型。
(3)文献[41]将缓冲算子的构造与函数结合起来,为缓冲算子的构造开辟了新方向,文献[49]对缓冲算子公理进行了补充,并构造了变权缓冲算子。本选题在他们的工作的基础上,构造了一类缓冲算子,整合了这些常用的缓冲算子,使得常用缓冲算子更一般化了,也更加灵活了。
(4)在现有灰色系统缓冲算子公理体系下,本文得到了以下结果:设D为一强化(或弱化)缓冲算子,X?(x(1),x(2),?,x(n))为系统原始行为数据序列,其缓冲序列为XD?(x(1)d,x(2)d,?x(n)d),f,g均为单调函数,并具有相同的单调性,且满足g(f(x(k)?,k?1,2,?,n,XD1?(x(1)d1,x(2)d1,?x(n)d1),其中))x(k
26
第6章 结论与展望
x(k)d1?g[f(x(k))d],则无论X为单调增长序列,单调衰减序列还是振荡序列, D1均为强化(或弱化)缓冲算子。
6.2 研究展望
由于本人对灰色系统理论的研究尚浅,对灰系统理论中一些看法还不够成熟,所做的工作中还有很多需要改进的地方,但笔者相信已具有发现问题并解决问题的能力,在今后的学习生活及工作,笔者会继续对灰色系统理论的研究,争取做出成绩,目前看来,笔者认为有以下几个方面可以进行研究:
(1)进一步深入研究灰模型的适用范围
(2)由于GM(1,1)模型的优化只有更优,没有最优,将继续分析模型误差产生的原因,并研究GM(1,1)模型的优化.
(3)将对缓冲算子的选用上以及从理论上研究通过缓冲算子作用以后能否从根本上提高模型精度进行研究
(4)由于目前灰数的运算不具有可逆性,将从理论上在这方面做些工作.
27
参考文献
参 考 文 献
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9] 邓聚龙(2002). 灰预测与灰决策[M].武汉:华中科技大学出版社. 刘思峰,党耀国,方志耕等.灰色系统理论及其应用[M].北京:科学出版社,2004. 罗党,刘思峰,党耀国(2003). 灰色模型GM(1 ,1) 优化[J] . 中国工程科学, 2003 (8) : 50 -53. 王正新,党耀国,刘思峰(2008). 基于离散指数函数优化的GM(1,1)模型[J]. 系统工程理论与实践,2: 61~67. 王义闹, 刘开第, 李应川(2001). 优化灰导数白化值的GM(1,1) 建模法[J]. 系统工程理论与实践,21(5):124-128. 刘思峰,邓聚龙(2000).GM(1,1)模型的适应范围[J]. 系统工程理论与实践,20(5):121-124. 薛焕斌,魏勇(2009). 基于离散指数函数优化的GM(1,1)模型的再优化[J]. 数学实践与认识, (1): 242-246. 穆勇. 具有白指数律重合性的GM(1,1)模型[J]. 数学的实践与认识,2002.1(1):15-19. 谢乃明,刘思峰. 离散GM(1, 1)模型与灰色预测模型建模机理[J]. 系统工程理论与实践,
2005, (1): 93-98.
[10] Nai-ming Xie, Si-feng Liu. Discrete Grey Forecasting Model and Its Optimization [J]. Applied
Mathematical Modeling, 2008, 33(2):1173-1186.
[11] Xiao Xinping, Deng Julong. A New Modified GM(1,1)Model[J]. Journal of systems
engineering and electronics, 2001, 12(2):1-5.
[12] Deng Julong. A Novel Grey Model GM (1, 1|r, r): Generalizing GM (1, 1) [J]. The Journal of
Grey System, 2001, 13(1):1-8.
[13] Deng Julong. Solution of Grey Differential Equation for GM (1, 1|r, r) in Matrix Train[J]. The
Journal of Grey System, 2002, 14(1):105-110.
[14] Deng Julong. Undulating Grey Model GM (l, 1|tg (k-r) p, sin (k-r) p) [J].The Journal of Grey
System, 2001, 13(3):201-204.
[15] 谢乃明,刘思峰. 离散灰色模型的仿射特性研究[J]. 控制与决策, 2008, 23(2): 200-203.
[16] 谢乃明,刘思峰. 多变量离散灰色模型及其性质[J]. 系统工程理论与实践, 2008, (6):
[17] Yanna Sun,Yong Wei , Optimization of Grey Derivative in GM (1, 1) Based on the Discrete
Exponential Sequence,2nd International Symposium on Information Processing, Huangshan, China, 2009: 313~315.
[18] 史玉峰,宁津生. 指数平滑法改进灰色模型及其在形变数据分析中的应用[J]. 煤炭学报,
2005.4(2):206-209.
[19] 史玉峰,靳奉祥,马健. 参数修正法改进灰色预测模型及其在岩土工程变形信息分析中的
应用[J]. 有色金属,2002.5(3):26-27.
[20] 李俊峰,戴文战. 基于插值和Newton-Cores公式的GM(1,1)模型的背景值构造新方法
与应用[J]. 系统工程理论与实践,2004.10(10):122-126.
[21] 谭冠军. GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J]. 系统工程理论与实践,2000.4
(4):98-103.
[22] 谭冠军. GM(1,1)模型的背景值构造方法和应用(Ⅱ)[J]. 系统工程理论与实践,2000.5
(5):125-127.
[23] 谭冠军. GM(1,1)模型的背景值构造方法和应用(Ⅲ)[J]. 系统工程理论与实践,2000.6
(6):70-74.
[24] 党耀国,刘思峰,刘斌. 以x(1)(n)为初始条件的GM模型[J]. 中国管理科学,2005.(1) :
132-134.
[25] 罗党,刘思峰,党耀国. 灰色模型GM(1,1)优化 [J]. 中国工程科学,2003.(8) :50-53.
[26] 张大海,江世芳,史开泉. 灰色预测公式的理论缺陷及改进[J]. 系统工程理论与实践,2002
28
参考文献
(8):140-142.
[27] kang Xiaoqing,wei Yong. Optimization of Non- equidistance GM(1,1) Model[C]. Proceedings
of the 5th Innovation & Management, 2008, 2:3031-3036.
[28] X.Q.Kang, Y.Wei. A New Optimized Method of Non-Equigap GM(1,1) Model[J]. The Journal
of Grey System, 2008, 20 (4): 375~382.
[29] 李翠凤,戴文战. 基于函数cotx 变换的灰色建模方法[J]. 系统工程,2005,(23):110~114.
[30] P. Zhou, Y.Wei. The Optimization of Background Value in Grey Model GM(1,1) [J]. Journal of
Grey System (TW), 2006(02):139-142.
[31] 李翠凤, 戴文战. 非等间距GM(1,1)模型背景值构造方法及应用[J]. 清华大学学报(自然科
学版), 2007, (47):1729~1732.
[32] 穆勇, 李素昉. 基于小生境遗传算法的非等间隔灰色直接模型[J]. 数学的实践与认
识,2004, (34):29~31.
[33] 王丰效. 多变量非等间距GM(1,m)模型及其应用[J]. 系统工程与电子技术, 2007.
[34] 史雪荣, 王作雷, 张正娣. 变参数非等间距GM(1,1)模型及应用[J]. 数学的实践与认识,
2006, (36):216~220.
[35] 王钟羡, 吴春笃, 史雪荣. 非等间距序列的灰色模型[J]. 数学的实践与认识, 2003,
(10):16~20.
[36] 史玉峰,宁津生. 指数平滑法改进灰色模型及其在形变数据分析中的应用[J]. 煤炭学报,
2005.4(2):206-209
[37] 罗佑新, 周继容. 非等间距GM (1,1) 模型及其在疲劳试验数据处理和疲劳试验在线检测
中的应用[J ]. 机械强度, 1999, 18 (3).
[38] 王丰效,郭天印(2007) ,. 基于中心逼近的非等距灰色模型[J ] .陕西理工学院学报, 23 (2) :78
- 81.
[39] 戴文战, 李俊峰. 非等间距GM(1,1)模型建模研究[J]. 系统工程理论与实践, 2005, (9):
89~93.
[40] 王叶梅,党耀国,王正新(2008),非等间距GM(1 ,1) 模型背景值的优化,中国管理科学,
16(4):159-162
[41] 吴正朋, 刘思峰, 米传民,崔立志, 张 可, 王建玲.基于单调函数的若干实用强化缓冲算
子的构造.系统 工程20xx年5月124-126
[42] 王正新, 党耀国, 刘思峰.变权缓冲算子及其作用强度的研究.控制与决策.2009 年8
月:1218-1222
[43] 党耀国,刘思峰,刘斌,等.关于弱化缓冲算子的研究[J].中国管理科学,2004,12(2):108-111.
[44] Yanna Sun,Yong Wei , A kind of Practical Strengthening Buffer Operator Based on the
Monotone Function[J],Journal of Systems Science and Information,2010,Vol.8,№.2: 103~108.
[45] 崔立志 , 刘思峰 , 吴正朋. 关于新的弱化缓冲算子的研究及其应用.控 制 与 决
策 2009 年8 月1252-1256
[46] 关叶青, 刘思峰.基于辅助函数的强化缓冲算子及其作用统计与决策2007 年3 月( 理论
版)20-21
[47] 谢乃明,刘思峰. 强化缓冲算子的性质与若干实用强化算子的构造[J]. 统计与决策,
2006(4):9-10.
[48] 高岩,周德群,刘晨琛.指数型强化缓冲算子的构造及其应用.统计与决策2009 年第2 期
8-10
[49] 王正新, 党耀国, 刘思峰.变权缓冲算子及缓冲算子公理的补充.系统工程,20xx年1
月:113-117
[50] 崔杰, 党耀国. 一类新的弱化缓冲算子的构造及其应用[J]. 控制与决
策,2008,23(7):741-750.
[51] 关叶青, 刘思峰.关于弱化缓冲算子序列的研究[J]. 中国管理科学,2007,15(4):89-92.
[52] 关叶青, 刘思峰.强化缓冲算子序列与m阶算子作用研究[J].云南师范大
学,2007,27(1):32-35.
[53] 党耀国,刘思峰,米传民.强化缓冲算子性质的研究[J]. 控制与决策,2007,22(7):730-734.
[54] 关叶青, 刘思峰. 基于不动点的强化缓冲序列算子及其应用[J]. 控制与决
策,2007,22(10):1189-1192.
29
参考文献
[55] 吴正朋, 刘思峰, 崔立志, 米传民, 王建玲.基于单调函数的新弱化缓冲算子研究.控 制
与 决 策 2009 年7 月1055-1058
[56] 党耀国,刘斌,关叶青. 关于强化缓冲算子的研究[J]. 控制与决策,2005,20(12):1332-1336.
30
致 谢
致 谢
本文是在导师魏勇教授的亲切关怀和悉心指导下完成的。教授渊博的理论知识、严谨的治学态度、活跃的创造性思维、崇高的教学风范以及开拓进取的精神使我受益匪浅,必将激励我在以后的学习、研究和工作中不断进取。在我论文撰写过程中,魏老师在繁忙的工作之余抽出时间认真审阅、批改,并给了我很多好的建议。我取得的每一点成绩和进步,都凝结着恩师大量的心血。导师为人处世的作风也是我值得学习的榜样。在此,谨向敬爱的恩师致以真诚的敬意和衷心地感谢!
另外,感谢西华师范大学数学与信息学院的各位领导和老师在生活上提供的诸多帮助以及学习上的不断鼓励。感谢同班同学在学习上的支持和帮助!感谢几位室友及各位师弟师妹的关心、支持和帮助!
还要感谢所有参考文献的作者,你们的工作是我汲取学术营养的土壤。
最后,谨以此不成熟的论文献给养育我二十多年的父母和亲人,长久以来,无论风雨,无论是成功还是失败,他们一直在背后给我以默默的支持和无尽的鼓舞,二十多年的风风雨雨,他们为我的成长付出了很多很多,正是有了他们的关怀和几十年的辛苦工作,才有了现在的我,希望能以此带给他们一些慰籍。
i
关于学位论文使用授权的声明
关于学位论文使用授权的声明
本人在导师指导下完成的本硕士学位论文,知识产权归本人和西华师范大学共有。
本人完全了解西华师范大学有关收集、保存、使用学位论文的规定,同意学校保存或向国家有关部门或机构送交论文的纸质版和电子版,允许论文被查阅和借阅。
本人授权西华师范大学可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用任何复制手段保存和汇编本学位论文。
本人离校后发表本学位论文中的成果时,第一署名单位应为西华师范大学。
保密论文在解密后应遵守此规定。
论文作者签名:
指导教师签名:
日 期: 年 月 日
ii
关于学位论文原创性的声明
关于学位论文原创性的声明
本人郑重声明:本人所呈交的学位论文,是在导师的指导下独立进行研究所取得的成果。学位论文中凡引用他人已经发表或未发表的成果、数据、观点等,均已明确注明出处。除文中已经注明引用的内容外,不包含任何其他个人或集体已经发表或撰写过的作品或科研成果。对本文的研究成果做出重要贡献的个人和集体,均已在文中以明确方式标明。
本声明的法律责任由本人承担。
论文作者签名:
指导教师签名:
日 期: 年 月 日
iii
在学期间的科研情况
iv
