考研数学:微积分考点总结
一、历年微积分考试命题特点
微积分复习的重点根据考试的趋势来看,难度特别是怪题不多,就是综合性串题。以往考试选择填空题比较少,而今年变大了。微积分一共74分,填空、选择占32分。第一是要把基本概念、基本内容有一个系统的复习,选择填空题很重要。几大运算,一个是求极限运算,还有就是求导数,导数运算占了很大的比重,这是一个很重要的内容。当然,还有积分,基础还是要把基本积分类型基础搞清楚,定积分就是对称性应用。二重积分就是要分成两个累次积分。三大运算这是我们的基础,应该会算,算的概念比如说极限概念、导数概念、积分概念。
二、微积分中三大主要函数
微积分处理的对象有三大主要函数,第一是初等函数,这是最基础的东西。在初等函数的基础上对分段函数,在微积分的概念里都有分段函数,处理的一般方法应该掌握。还有就是研究生考试最常见的是变限积分函数。这是我们经常遇到的三大基本函数。
三、微积分复习方法
微积分复习内容很多,题型也多,灵活度也大。怎么办呢?这其中有一个调理办法,首先要看看辅导书、听辅导课,老师给你提供帮助,会给你一个比较系统的总结。老师总结的东西,比如说我在辅导课程中总结了很多的点,每一个点要掌握重点,要举一反三搞清楚。从具体大的题目来讲,基本运算是考试的重要内容。应用方面,无非是在工科强调物理应用,比如说旋转体的面积、体积等等。在经济里面的经济运用,弹性概念、边际是经济学的重要概念,包括经济的函数。还有一个更应该掌握的,比如集合、旋转体积应用面等等,大的题目都是在经济基础上延伸出的问题,只有数学化了之后,才能处理数学模型。
还有中值定理,还有微分学的应用,比如说单调性、凹凸性的讨论、不等式证明等等。应用部分包括证明推断的内容。
总的来说,学好微积分,就是要掌握三个基本函数、三大运算,所以广大研友们要在这些方面多下功夫!
凯程考研:
凯程考研成立于20##年,具有悠久的考研辅导历史,国内首家全日制集训机构考研,一直从事高端全日制辅导,由李海洋教授、张鑫教授、卢营教授、王洋教授、杨武金教授、张释然教授、索玉柱教授、方浩教授等一批高级考研教研队伍组成,为学员全程高质量授课、答疑、测试、督导、报考指导、方法指导、联系导师、复试等全方位的考研服务。
凯程考研的宗旨:让学习成为一种习惯;
凯程考研的价值观:凯旋归来,前程万里;
信念:让每个学员都有好最好的归宿;
使命:完善全新的教育模式,做中国最专业的考研辅导机构;
激情:永不言弃,乐观向上;
敬业:以专业的态度做非凡的事业;
服务:以学员的前途为已任,为学员提供高效、专业的服务,团队合作,为学员服务,为学员引路。
特别说明:凯程学员经验谈视频在凯程官方网站有公布,同学们和家长可以查看。扎扎实实的辅导,真真实实的案例,凯程考研的价值观:凯旋归来,前程万里。
如何选择考研辅导班:
在考研准备的过程中,会遇到不少困难,尤其对于跨专业考生的专业课来说,通过报辅导班来弥补自己复习的不足,可以大大提高复习效率,节省复习时间,大家可以通过以下几个方面来考察辅导班,或许能帮你找到适合你的辅导班。
师资力量:师资力量是考察辅导班的首要因素,考生可以针对辅导名师的辅导年限、辅导经验、历年辅导效果、学员评价等因素进行综合评价,询问往届学长然后选择。判断师资力量关键在于综合实力,因为任何一门课程,都不是由一、两个教师包到底的,是一批教师配合的结果。还要深入了解教师的学术背景、资料著述成就、辅导成就等。凯程考研名师云集,李海洋、张鑫教授、方浩教授、卢营教授、孙浩教授等一大批名师在凯程授课。而有的机构只是很普通的老师授课,对知识点把握和命题方向,欠缺火候。
对该专业有辅导历史:必须对该专业深刻理解,才能深入辅导学员考取该校。在考研辅导班中,从来见过如此辉煌的成绩:凯程教育拿下2015五道口金融学院状元,考取五道口15人,清华经管金融硕士10人,人大金融硕士15个,中财和贸大金融硕士合计20人,北师大教育学7人,会计硕士保录班考取30人,翻译硕士接近20人,中传状元王园璐、郑家威都是来自凯程,法学方面,凯程在人大、北大、贸大、政法、武汉大学、公安大学等院校斩获多个法学和法硕状元,更多专业成绩请查看凯程网站。在凯程官方网站的光荣榜,成功学员经验谈视频特别多,都是凯程战绩的最好证明。对于如此高的成绩,凯程集训营班主任邢老师说,凯程如此优异的成绩,是与我们凯程严格的管理,全方位的辅导是分不开的,很多学生本科都不是名校,某些学生来自二本三本甚至不知名的院校,还有很多是工作了多年才回来考的,大多数是跨专业考研,他们的难度大,竞争激烈,没有严格的训练和同学们的刻苦学习,是很难达到优异的成绩。最好的办法是直接和凯程老师详细沟通一下就清楚了。
凯程考研历年战绩辉煌,成就显著!
在考研辅导班中,从来见过如此辉煌的成绩:凯程教育拿下国内最高学府清华大学五道口金融学院金融硕士29人,占五道口金融学院录取总人数的约50%,五道口金融学院历年状元均出自凯程.例如,20##年状元武玄宇,20##年状元李少华,20##年状元马佳伟,20##年状元陈玉倩;考入北大经院、人大、中财、外经贸、复旦、上财、上交、社科院、中科院金融硕士的同学更是喜报连连,总计达到150人以上,此外,还有考入北大清华人大法硕的张博等10人,北大法学考研王少棠,北大法学经济法状元王yuheng等5人成功考入北大法学院,另外有数10人考入人大贸大政法公安大学等名校法学院。北师大教育学和全日制教育硕士辅导班学员考入15人,创造了历年最高成绩。会计硕士保录班考取30多人,中传郑家威勇夺中传新闻传播硕士状元,王园璐勇夺中传全日制艺术硕士状元,(他们的经验谈视频在凯程官方网站有公布,随时可以查看播放。)对于如此优异的成绩,凯程辅导班班主任邢老师说,凯程如此优异的成绩,是与我们凯程严格的管理,全方位的辅导是分不开的,很多学生本科都不是名校,某些学生来自二本三本甚至不知名的院校,还有很多是工作了多年才回来考的,大多数是跨专业考研,他们的难度大,竞争激烈,没有严格的训练和同学们的刻苦学习,是很难达到优异的成绩。
考研路上,拼搏和坚持,是我们成功的必备要素。
王少棠
本科学校:南开大学法学
录取学校:北大法学国际经济法方向第一名
总分:380+
在来到凯程辅导之前,王少棠已经决定了要拼搏北大法学院,他有自己的理想,对法学的痴迷的追求,决定到最高学府北大进行深造,他的北大的梦想一直激励着他前进,在凯程辅导班的每一刻,他都认真听课、与老师沟通,每一个重点知识点都不放过,对于少棠来说,无疑是无比高兴的是,圆梦北大法学院。在复试之后,王少棠与凯程老师进行了深入沟通,讲解了自己的考研经验,与广大考北大法学,人大法学、贸大法学等同学们进行了交流,录制为经验谈,在凯程官方网站能够看到。
王少棠参加的是凯程考研辅导班,回忆自己的辅导班的经历,他说:“这是我一辈子也许学习最投入、最踏实的地方,我有明确的复习目标,有老师制定的学习计划、有生活老师、班主任、授课老师的管理,每天6点半就起床了,然后是吃早餐,进教室里早读,8点开始单词与长难句测试,9点开始上课,中午半小时吃饭,然后又回到教室里学习了,夏天比较困了就在桌子上睡一会,下午接着上课,晚上自习、测试、答疑之类,晚上11点30熄灯睡觉。”
这样的生活,贯穿了我在辅导班的整个过程,王少棠对他的北大梦想是如此的坚持,无疑,让他忘记了在考研路上的辛苦,只有坚持的信念,只有对梦想的勇敢追求。
龚辉堂
本科西北工业大学物理
考入:五道口金融学院金融硕士(原中国人民银行研究生部)
作为跨地区跨校跨专业的三跨考生,在凯程辅导班里经常遇到的,五道口金融学院本身公平的的传统,让他对五道口充满了向往,所以他来到了凯程辅导班,在这里严格的训练,近乎严苛的要求,使他一个跨专业的学生,成功考入金融界的黄埔军校,成为五道口金融学院一名优秀的学生,实现了人生的重大转折。
在凯程考研辅导班,虽然学习很辛苦,但是每天他都能感觉到自己在进步,改变了自己以往在大学期间散漫的学习状态,进入了高强度学习状态。在这里很多课程让他收获巨大,例如公司理财老师,推理演算,非常纯熟到位,也是每个学生学习的榜样,公司理财老师带过很多学生,考的非常好。在学习过程中,拿下了这块知识,去食堂午餐时候加一块鸡翅,经常用小小的奖励激励自己,寻找学习的乐趣。在辅导班里,学习成绩显著上升。
在暑期,辅导班的课程排得非常满,公共课、专业课、晚自习、答疑、测试,一天至少12个小时及以上。但是他们仍然特别认真,在这个没有任何干扰的考研氛围里,充实地学习。
在经过暑期严格的训练之后,龚对自己考入五道口更有信心了。在与老师沟通之后,最终确定了五道口金融学院作为自己最后的抉择,决定之后,让他更加发奋努力。
五道口成绩公布,龚辉堂成功了。这个封闭的考研集训,优秀的学习氛围,让他感觉有质的飞跃,成功的喜悦四处飞扬。
另外,在去年,石继华,本科安徽大学,成功考入五道口金融学院,也就是说,我们只要努力,方向正确,就能取得优异的成绩。师弟师妹们加油,五道口、人大、中财、贸大这些名校等着你来。
黄同学(女生)
本科院校:中国青年政治学院
报考院校:中国人民大学金融硕士
总分:跨专业380+
初试成绩非常理想,离不开老师的辛勤辅导,离不开班主任的鼓励,离不开她的努力,离不开所有关心她的人,圆梦人大金融硕士,实现了跨专业跨校的金融梦。
黄同学是一个非常腼腆的女孩子,英语基础算是中等,专业课是0基础开始复习,刚刚开始有点吃力,但是随着课程的展开,完全能够跟上了节奏。
初试成绩公布下来,虽然考的不错,班主任老师没有放松对复试的辅导,确保万无一失,拿到录取通知书才是最终的尘埃落地,开始了紧张的复试指导,反复的模拟训练,常见问题、礼仪训练,专业知识训练,每一个细节都训练好之后,班主任终于放心地让她去复试,果然,她以高分顺利通过复试,拿到了录取通知书。这是所有凯程辅导班班主任、授课老师、生活老师的成功。
张博,从山东理工大学考入北京大学法律硕士,我复习的比较晚,很庆幸选择了凯程,法硕老师讲的很到位,我复习起来减轻了不少负担。愿大家在考研中马到成功,也祝愿凯程越办越好。
张亚婷,海南师范大学小学数学专业,考入了北京师范大学教育学部课程与教学论方向,成功实现了自己的北师大梦想。特别感谢凯程的徐影老师全方面的指导。
孙川川,西南大学考入中国传媒大学艺术硕士,播音主持专业。在考研辅导班,进步飞快,不受其他打扰,能够全心全意投入到学习中。凯程老师也很负责,真的很感谢他们。
在凯程考研辅导班,他们在一起创造了一个又一个奇迹。从河南理工大学考入人大会计硕士的李梦说:考取人大,是我的梦想,我一直努力,肯定能够成功的,只要我们不放弃,不抛弃,并且一直在努力前进创造成功的条件,每个人都能够成功。正确的方法+不懈的努力+良好的环境+严格的管理=成功。我相信,每个人都能够成功。
第二篇:考研数学思路班微积分第一讲
知识宝库考研社区()友情提示:购买原版,饮水思源!
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
解题思路班第1讲 微积分上
清华大学数学科学系 刘坤林
?极限、连续与可导问题解题思路
?函数性态研究1:函数与导函数的零点问题
?函数性态研究2:增减性与凸性、极值点与拐点、不等式分析与证明问题
?积分技巧训练、定积分概念与性质综合问题
?定积分应用问题
?级数的收敛性分析、幂级数展开与求和
1.极限、连续与可导问题解题思路
极限定义与性质,四则与复合运算法则,标准极限(含导数定义,共三个),无
穷小量与无穷大量排序,极限存在准则,无穷小量替换,罗必达法则,用定积
分定义求极限,若干可供利用的极限结论。
处理极限问题的原则:摸着石头过河。
极限与点连续的等价描述,点连续的三要素,点连续的重要性质运用。
闭区间上连续函数的性质(三条),开区间上连续函数的情况。 1
1-1 lim(cosx)ln(1+x)= . 【答】 x→0
11. e1cosx?1?cosx?1ln(1+x2)【解】(方法1) lim(cosx)ln(1+x
x→02)=lim(1+cosx?1)x→0
limcosx?1=limx→0ln(1+x2)x→0?121x1?1ln(1+x)=?,lim(cosx)=e2。 2x2x→0
(方法2)
1
ln(1+x)lim(cosx)x→0=ex→0ln(1+x2)lim1lncosx,
?sinx
lncosxlncosx=?1, limlim==而 limx→0ln(1+x2)x→0x→0x22x2
故 原式=e?1
2=1
.
1刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
11-2(本题满分10分)求极限lim3x→0x
e??2+cosx?x???1?. ??3???????1 【解】(方法1)原式=limx→0?2+cosx?xln??3??x3
?2+cosx?ln??3?=lim?
2 x→0x
ln(2+cosx)?ln3=limx→0x2
1?(?sinx)=limx→0 2x
11sinx1=?lim?=?2x→02+cosxx6.
?2+cosx?xln??3??
(方法2)原式=limx→0ex3?2+cosx?ln???13? =lim?
x→0x2
?cosx?1?ln?1+?3??=limcosx?1=?1. =limx→0x→06x23x2
?1cos2x??2?1-3(本题满分8分)求 lim?。 ?x→0?sin2xx??
?1cos2
?【解】lim?x→0?sin2xx2?x??? ?
2?1sin22xxx2?sin2xcos2x =lim=lim422x→0x→0xsinxx
x?
=limx→01sin4x1?cos4x(4x)24limlim=== x→0x→02?6x22x36x23
1-4 (12分) 设数列{xn}满足0<x1<π,xn+1=sinxn(n=1,2,K)。
xx2(Ⅰ)证明limxn存在,并求其值 。 (Ⅱ)计算lim(n+1)n 。 n→∞n→∞xn
2刘坤林编 清华大学东门外 创业大厦1006
1
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
【解】 (1)x2=sinx1,0<x2≤1,,因此当n≥2时
xn+1=sinxn≤xn,{xn}单调减少。又xn≥0,即{xn}有下界,有极限存在
准则,limxn=A存在,再由极限的唯一性,将递推公式两边取极限得n→∞
A=sinA,解得A=0。
sinxnxn12xn(2)原式=lim(n→∞,为"1∞"型
(方法1)对离散型不能直接用洛必达法则,先考虑
11sint)ln(sintt2t2t,由复合极限定理,只需考虑 lim()=limet→0t→0t
cost?111sint?t=?=limlim226tt→03tt→0 因此lim(n→∞sinxnxn12xn11?sintt2=lim(=e6。 t→0t
(方法2) 利用重要极限凑成标准型:
1sint?t1t
sintt2sint?tsint?t2 lim()=lim{(1+)]t
0t→0t→tt
由复合极限定理,再考虑如下极限即可:
limt→01sint?tcost?11lim==?2t→0t6。 3t2
参见水木艾迪2006考研数学36计例1-7,基础班例4.41,强化班第1讲例
14,例19,例23,水木艾迪2006考研数学模拟试题第八套数四第(2)题等题
目。还可参见清华大学出版社《大学数学考研清华经典备考教程 微积分上》(刘
坤林、谭泽光编写)第5章综例5.4.8。
1-5 (10分)试确定A,B,C的常数值,使e(1+Bx+Cx)=1+Ax+ο(x)
其中ο(x)是当x→0时比x的高阶无穷小。. 33x23
x2x3
【解析与点评】将e=1+x+++ο(x3)代入已知等式左端得 26x
3刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
x2x3[1+x+++ο(x3)][1+Bx+Cx2]=1+Ax+ο(x3) 26整理并比较两边同次幂函数得 11??B1+(B+1)x+(C+B+)x2+?+C+?x3+ο(x3)=1+Ax+ο(x3) 26??2B+1=A ①
1C+B+=0 ② 2
B1+C+=0 ③ 26
211B1由式②-③得 +=0,B=?,A=,C=。 33623
参见清华大学出版社《考研通用教材》(考研数学应试导引与进阶)微积分
(上)例6.48, 水木艾迪2006考研数学强化班第1讲例40等题。
1-6(本题满分11分) 设函数f(x)连续,且f(0)≠0,求极限
∫limx→0x0(x?t)f(t)dtx。
x∫0f(x?t)dt
【解析与点评1】 本题主要考点是:(1)含参积分处理方法;(2)极限分析计
算与罗必达法则;(3)变限积分求导数;(4)积分中值定理。水木艾迪考研辅
导班教学中含有不少此类例题,可参见基础班综合辅导第2讲例 2.21,例2.25,
例2.27,水木艾迪考研辅导暑期强化班第4讲例39-43,例55-56等例题,系列
教材《2005考研数学应试导引与进阶》中也有许多这样的典型例题和方法,如
例6.74,例6.78,例7.22等。刘坤林等编写,清华大学出版社20xx年7月出
版。
【解】 首先对分母取区间变换u=x?t,则
∫
x0f(x?t)dt=∫f(u)d(?u)=∫f(u)du=∫f(t)dt, x0xx00 ∫limx→0x0(x?t)f(t)dtx
0x∫f(x?t)dt=limx→0x∫f(t)dt?∫tf(t)dt00xxx∫f(t)dt0x
=limx→0∫∫x
0x0f(t)dt=limx→0f(t)dt+xf(x)f(ξ)xf(0)1== f(ξ)x+xf(x)f(0)+f(0)2
其中0<ξ<x,x→0时ξ→0,上述第2个等号用了罗必达法则。
【解析与点评2】 我们在水木艾迪考研辅导班教学中则特别强调(1)遇到含
4刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
参数的积分时,首先采用区间变换处理参数问题;(2)在含有函数及其积分同
时出现在一个表达式的情形下,有效方法是采用积分中值定理脱掉积分号,包
括等式不等式证明,以及极限分析计算问题,这是重要的技巧。此题目对水木
艾迪学员考生来讲,拿到这11分只需要3-5分钟。
1-7 曲线y=323(1+x) y=x+ 2x
【解析与点评1】 作为斜渐近问题,其实质是极限问题。本题是一个基本题目。
但是计算上却有一点点技巧。因此除渐近线以外考点以外的主要考点是极限运
算,特别是无穷小量替换((x+1)?1~λx(λ∈R))的正确使用。 λ
a=limx→∞(1+x)x1=lim(+1)=1, x→∞x
(1+x)b=lim[x→∞x?x]=limx→∞(1+x)?xx
1313=limx[(1+?1]=limx??=。 x→∞x→∞x2x2
【解析与点评2】 在水木艾迪考研辅导教学中,我们特别强调在极限运算中,
要注意两点:(1)正确使用极限运算法则;(2)在尽可能的情况下,优先考虑
无穷小量替换,特别在有理化处理或应用罗必达法则之前,应优先考虑采用无
穷小量替换,以简化代数运算或导数运算的复杂性。本考题计算b的另外做法,
可以是有理化处理、应用罗必达法则或泰勒展开,但过程会复杂的多
1-8 设函数f(x)=1
ex
x?1,则( D ) ?1
(A)x=0,x=1都是f(x)的第一类间断点。 (B)x=0,x=1都是f(x)的第二类间断点。 (C)x=0是f(x)的第一类间断点,x=1是f(x)的第二类间断点。 (D)x=0是f(x)的第二类间断点,x=1是f(x)的第一类间断点。
xx
x→?∞x→+∞【解析与点评1】 一个基本结论是lime=0,lime=+∞ ,或
1
x1x
x→0?lime=0,lime=+∞。 +x→0
这一结论可以变换各种不同花样(复合函数)进行命题,是水木艾迪考研辅导
教学中强调的星级考点之一。本考题解法如下
【解】 limx→01ex
x?1,因此x=0是f(x)的第二类间断点。 =∞(不存在)?1
5刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
x→1lim?
e1x
x?1=?1,lim+?1x→11ex
x?1=0≠?1,因此x=1是f(x)的第一类间断点。?1
答案D 。
【解析与点评2】 本题目的主要考点是:(1)基本初等函数性质与极限状态的
结论;(2)连续函数与间断点的分类。本题即为水木艾迪考研辅导系列教材《2005
考研数学应试导引与进阶》中的模拟自测题 2.18(刘坤林、谭泽光等编写,清
华大学出版社20xx年7月出版),还与水木艾迪考研辅暑期强化班第1讲例37
几乎完全一样。 ?1,x≠0,且x≠1x?模拟自测题 2.18:设函数f(x)=?1?e1?x,则( B )。
?x=0或1?0,
(A)x=0,x=1都是f(x)的可去间断点第一类间断点。 (B)x=0是f(x)的无穷间断点;x=1是f(x)的第一类间断点,但不为
可去间断点。
(C)x=0是f(x)的无穷间断点;x=1是f(x)的去间断点。
(D)x=0,x=1均为f(x)的第一类间断点。
答案:limx→01ex
x?1=∞,lim??1
2x→11e2xx?1=0,lim+?12x→11exx?1=?1。答案B。 ?11-9 limln?1+n→∞?
21??2????1+?L?1+n??n??2n??等于 [B] n?(Α)∫1ln2xdx. (Β)2∫1lnxdx.
(C)2∫2
1ln(1+x)dx. (D)∫ln2(1+x)dx. 1
2221??2???【解】limln?1+??1+?L?1+n→∞n??n???n?? n?2
=lim2?1??2??n?ln?1+??1+?L?1+? n→∞nn??n??n??
121n?k?=2lim∑ln?1+?=2∫ln(1+x)dx=2∫lntdt, 10n→∞n?n?k=1
答案 (B)。
?2?x2(1?cosx),x<0
?1-10 (本题满分6分) 设f(x)=?1, x=0,试讨论f(x)在x=0处的连续性和
?1x?∫cost2dt,x>0?x0
6刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
可导性.
【解】 (1)由 lim?x→02sinx()1?cos=lim=1,x2?x→0xx
1xcosx2
2limcostdt=lim=1, ∫++0x→0xx→01
可知limf(x)=1=f(0),于是,函数f(x)在x=0处连续, x→0
(2)分别求f(x)在x=0处的左、右导数.
f?′(0)=lim?x→01?2(1?cosx)??1? 2x?x??
2(1?cosx)?x22sinx?2x=lim?=limx→0x→0?x33x2
?sinx2cosx?2=lim?=lim?=0x→0x→036x
f+′(0)=lim+x→01?1x?2?∫0costdt?1? x?x?
cosx2?1 =lim+x→02x∫=limx→0+x0cost2dt?xx2
?2xsinx2
=lim+=0 x→02
由于左、右导数都等于0,可见f(x)在x=0处可导,且f′(0)=0。
1-11(2007-数一、二、三、四共用)设函数f(x)在x=0处连续,下列命题错误的是
f(x)存在,则f(0)=0 x→0x
f(x)+f(?x)(B)若lim存在,则f(0)=0 x→0x
f(x)(C)若lim存在,则f′(0) 存在 x→0x
f(x)?f(?x)(D)若lim存在,则f′(0)存在 x→0x(A)若lim
【解】利用无穷小量比阶概念,再由f(x)在x=0处连续,则(A)(B)正确;另由导数定义,
(C)正确。答案D。
考点:点连续概念,导数定义,无穷小量比阶的概念与极限运算法则。(D)的成立不一定保证导致可导的两个极限存在。请看错误做法:
7刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
f(x)?f(?x) x→0x
f(x)?f(0)f(?x)?f(0) =lim+limx→0x→0x?xlim
=f′(0)+f′(0)=2f′(0)
则f′(0)存在。极限运算法则错误!
1-12设数列xn与yn满足limxnyn=0则下列断言正确的是【 】 n→∞
(A)若xn发散,则yn必发散.。(B)若xn无界,则yn必有界.
(C)若xn有界,则yn必有无穷小。
(D)若1为无穷小,则yn必为无穷小. xn
1=0,所以(D)n→∞xn【解】 (方法一)由极限运算性质知 limyn=lim(xnyn)limn→∞n→∞
正确.
(方法二)取数列yn=0,排除(A)。
若取数列(都无界!)
?2k?1,n=2k?1?0,n=2k?1(k=1,2,L),yn=?(k=1,2,L),则排除xn=?n=kkn=k0,22,2??
了(B)。对于(C),若数列xn=0,则yn可为任意数列,所以(C)不正确。
故应选(D).
1-13(2002-2-10)已知f(x)在x=0的某领域内有二阶连续导数且
f(0)≠0,f′(0)≠0,f′′(0)≠0,证明存在唯一的一组实数λ1,λ2,λ3,
使得当h→0时λ1f(h)+λ2f(2h)+λ3f(3h)?f(0)是比h2高阶的无穷小量。
【证】 只须证明存在唯一的一组实数λ1,λ2,λ3使得 limh→0λ1f(h)+λ2f(2h)+λ3f(3h)?f(0)h2
h→0=0, lim[λ1f(h)+λ2f(2h)+λ3f(3h)?f(0)]
8刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
=λ1f(0)+λ2f(0)+λ3f(0)?f(0)=0
因f(0)≠0,于是 λ1+λ2+λ3=1。 另由洛必达法则又有
0=limh→0λ1f′(h)+2λ2f′(2h)+3λ3f′(3h)2h
=limh→0λ1f′′(h)+4λ2f′′(2h)+9λ3f′′(3h)2
1=λ1+4λ2+9λ3)f′′(0), 2
由连续函数概念与无穷小量比阶概念得到
limλ1f′(h)+2λ2f′(2h)+3λ3f′(3h)=(λ1+2λ2+3λ3)f′(0)=0 h→0
而f′(0)≠0,f′′(0)≠0,分别约去公因子,可得到
?λ1+λ2+λ3=1?, ?λ1+2λ2+3λ3=0,系数行列式不为零(范得蒙行列式)
?λ+4λ+9λ=023?1
于是λ1,λ2,λ3有为一解。
另外:亦可用二阶泰勒公式证明。 1-14 设函数f(x)=lim+xn→∞3n,则f(x)在(?∞,+∞)内 [C]
(B)恰有一个不可导点. (D)至少有三个不可导点. (A)处处可导。 (C)恰有两个不可导点.
【解析与点评】 函数的表达式可以是极限,导数,积分,或是级数。本题
f(x)=lim+xn→∞3n
是函数的定义式,实质是一个含参极限问题,处理的方法是对参数x分段讨论。
相关方法与雷同例题,可参见水木艾迪考研辅导系列教材《高等数学典型题题
典》(,刘坤林等编著,东北大学出版社,20xx年7月出版)中的例1.20与例
1.8, 以及水木艾迪考研辅导2004暑期班第1讲例6等。
当x≤1时,lim+xn→∞3n=1, 当x>1时,lim+xn→∞3n=xlim(n→∞31x3n+1)=x,因此 1n3
9刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
3nf(x)=lim+xn→∞??1,=?3??x,x≤1x>1, 只需考虑x=±1处的可导性。
?x3?11?1f?′(?1)=lim?=?3,f+′(?1)=lim+=0 x→?1x→?1x?1x?1
31?1x=0,f+′(1)=lim?1=3, f?′(1)=lim?x→1x?1x→1x?1+
由可导的充要条件,x=±1处均不可导,由初等函数的性质,在x≠±1的任意
点都可导。
本题考点:含参极限问题,极限运算,初等函数性质与连续函数概念,导数定
义与可导条件。
1-15 设y=(1+sinx),则dyx
x=π = ?πdx .
【分析】 本题属基本题型,幂指函数的求导(或微分)问题可化为指数函数求导或取对数后转化为隐函数求导.
【解】 (方法一) y=(1+sinx)=exln(1+sinx),于是
y′=exln(1+sinx)?[ln(1+sinx)+x?
从而 dy=y′(π)dx=?πdx. xcosx], 1+sinxx=π
(方法二) 两边取对数,lny=xln(1+sinx),对x求导,得
xcosx1, y′=ln(1+sinx)+y1+sinx
cosx,故 1+sinx于是 y′=(1+sinx)x?[ln(1+sinx)+x?
dy=y′(π)dx=?πdx. x=π
【提示】 应掌握幂指型函数作为复合对数幂函数的表达。
2.函数性态研究:函数与导函数的零点问题,有界性、增减性与凸性问题、极
值点与拐点问题、等式与不等式证明问题
2-1(2005共用考题)设函数f(x)连续,且f'(0)>0,则存在δ>0,使得
(A) f(x)在(0,δ)上单调增加。 (B) f(x)在(?δ,0)上单调增加。
(C) 对任意的x∈(0,δ)有f(x)>f(0)。 (D) 对任意的x∈(?δ,0)有f(x)>f(0)。
10刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055 f(x)?f(0)>0,则由极限保序性可推断存在δ>0,x→0x?0
f(x)?f(0)使当x∈(?δ,0)或x∈(0,δ)时,>0, x?0【证】答案(C).由 f′(0)=lim
即f(x)?f(0)与x应保持同号,因此:
对任意的x∈(0,δ)有f(x)>f(0),对任意的x∈(?δ,0)有
f(x)<f(0)。
注:此结论在水木艾迪考研辅导教学及教材中称为由导数正负号决定的函数局
部比较性质。只由一点处的导数正负号,不能决定函数的增减性。函数的增减
性属于区间上或全局性质。
且f'(a)>0,f'(b)<0,则下列结论中错误的是 2-2 设f'(x)在[a,b]上连续,??
[D]。
(A)至少存在一点x0∈(a,b),使得f(x0)>f(a).。
(B)至少存在一点x0∈(a,b),使得f(x0)>f(b).
(C)至少存在一点x0∈(a,b),使得f'(x0)=0.
(D)至少存在一点x0∈(a,b),使得f(x0)=0.
【提示】本题考点:极限保序性,由导数正负号决定的函数局部比较性质,连
续函数零点定理或导数零点定理。
2-3设f(x)f(x)在区间[a,b]上具有二阶导数,且
f(a)=f(b)=0,f′(a)f′(b)>0,证明:
存在ξ∈(a,b)和η∈(a,b),使f(ξ)=0及f′′(η)=0
【分析】本题考查的是介值性定理的应用。
【解】(方法1)用反证法,若不存在ξ∈(a,b),使f(ξ)=0,则在区间(a,b)
内恒有f(x)>0或f(x)<0,
不妨设f(x)>0(对f(x)<0,类似可证),则
f′(b)=lim?x→bf(x)?f(b)f(x)=lim?≤0, x→bx?bx?b
11刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
f′(a)=lim+x→af(x)?f(a)f(x)=lim+≥0 x→ax?ax?a
从而f′(b)f′(a)≤0,这与已知条件矛盾,即在(a,b)内至少存在一点ξ使
f(ξ)=0。
再由f(a)=f(ξ)=f(b)及罗尔定理,知存在η1∈(a,ξ)和η2∈(ξ,b),使
f′(η1)=f′(η2)=0,
η1,η2]上,对f′(x)应用罗尔定理,知存在η∈(η1,η2)?(a,b), 又在区间[
使f′′(η)=0
(方法2)不妨设f
即 lim+x→ax?a,(a)>0,f'(b)>0(对f′(b)<0,f′(a)<0时类似可证)f(x)f(x)>0,lim>0 '
x→b?x?a
由极限的保号性,存在x1∈(a,a+δ1)和x2∈(b?δ2,b)使得f(x1)>0及
f(x2)<0,其中δ1,δ2为充分小的正数,并且x1<x2,在区间[x1,x2]上应用
零点定理,于是存在ξ∈(x1,x2)?(a,b)使f(ξ)=0。
以下应用罗尔定理,同方法1。
2-4 (本题满分12分) 已知函数f(x)在[0,1]上连续,在(0,1)内可导,且
f(0)=0,f(1)=1。证明:
(I) 存在ξ∈(0,1),使得f(ξ)=1?ξ;
(II) 存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1。
【解析与点评】 (I) 在函数分析的证明题中,对这类问题中的等式或不等式证
明,直接有效的方法是将欲证的等式或不等式进行移项,取一个相应的辅助函
数,对等式问题:以连续函数零点定理为主线进行分析;对不等式:用导数作
为工具考察辅助函数的增减性,同时考虑函数在所论区间上的的初值与终值,
(开区间则需考虑单测极限。还可参见2005数三数四底19题。这类问题是水
木艾迪考研辅导班教学中的重点方法训练。相仿可参见水木艾迪考研辅导2005
突破百分训练营第1-55题。相关概念、题型与方法可参考水木艾迪考研辅导系
列教材《2005考研数学应试导引与进阶》与《大学数学---概念方法与技巧》(均
为刘坤林等编著,清华大学出版社出版),以及水木艾迪考研辅导系列教材《高
12刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
等数学典型题题典》(刘坤林等编著,东北大学出版社)。
令g(x)=f(x)+x?1,则g(x)在[0,1]上连续,且
g(0)=?1<0,g(1)=1>0,由连续函数零点定理,存在ξ∈(0,1)使得
g(ξ)=f(ξ)+ξ?1=0,即 f(ξ)=1?ξ。
(II) 此类问题的有效方法是由函数的零点(有时是驻点),将所论的区间分
成子区间,进一步的分析即可得到结果。这是水木艾迪考研辅导班教学中的常
规基本方法训练。可参见水木艾迪考研辅导强化班第1讲例35与39,第2讲
例31,还可参见《2005考研数学应试导引与进阶》中例4.30,以及水木艾迪
考研辅导系列教材《高等数学典型题题典》,中的模拟自测题2-110(刘坤林等
编著,东北大学出版社,20xx年7月出版),且与水木艾迪考研辅导2005突破
百分训练营数模2-43题相雷同。
根据拉格朗日中值定理,存在η∈(0,ξ),ζ∈(ξ,1),使得成立以下两式成
立: f′(η)=f(ξ)?f(0)
ξ=1?ξ
ξ
f′(ζ)=ξf(1)?f(ξ)1?(1?ξ)==, 1?ξ1?ξ1?ξ
f′(η)f′(ζ)=1?ξ?所以 ξ
1?ξξ=1.
2-5 设f(x)在[a,b]上可导,且f(a)=f(b)=1,试证存在ξ,η∈(a,b),使
得 eη?ξ[f(η)+f′(η)]=1
x【解】 令F(x)=ef(x),则F(x)在[a,b]上满足Lagrange
定理条件,于是
ebf(b)?eaf(a)=eη[f(η)+f′(η)],其中η∈(a,b) b?a
eb?ea
由f(a)=f(b)=1,则有=eη[f(η)+f′(η)], b?a
eb?ea
另取g(x)=e,则又有=eξ,其中ξ∈(a,b), b?ax
综合上述两个等式即有 eη?ξ[f(η)+f′(η)]=1
13刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
2-6 设f(x)在区间[a,b]上连续,在(a,b)可导,证明:在(a,b)内至少存在
一点ξ,使bf(b)?af(a)=f(ξ)+ξf′(ξ). b?a
【解】 (方法一:拉格朗日中值定理)
作辅助函数F(x)=xf(x)则f(x)在[a,b]上满足拉格朗日中值定理的条
F(b)?F(a)=F′(ξ) b?a
bf(b)?af(a)由于F′(x)=f(x)+xf′(x) , 可见=f(ξ)+ξf′(ξ) . b?a件,从而在(a,b)内存在一点ξ,使
(方法二:罗尔定理)将ξ视为x,移项造辅助函数 。考虑
bf(b)?af(a)=f(x)+xf′(x), b?a
bf(b)?af(a)即?[xf(x)]′=0,积分得辅助函数为 b?a
bf(b)?af(a)F(x)=x?xf(x) b?a
则F(x)在[a,b]上连续,在(a,b)内可导,且F(a)=F(b)=0 ,
由罗尔定理知,存在ξ∈(a,b) ,使得F′(ξ)=0,即 bf(b)?af(a)=f(ξ)+ξf′(ξ)。 b?a
2-7设函数f(x)在闭区间[?1,1]上具有三阶连续导数,且
f(?1)=0,f(1)=1,f′(0)=0证明:在开区间(?1,1)内至少存在一点ξ使
f′′′(ξ)=3.
【分析】可用函数的幂级数展开式以及连续函数的有界性进行计算,也可以用
中值定理。
【解】在x=0处,将f(x)按泰勒公式展开,得
f(x)=f(0)+f′(0)x+11f′′(x)x2+f′′′(η)x3 2!3!
其中η介于0与x之间,x∈[?1,1]
分别令x=?1和x=1,并结合已知条件,得
0=f(?1)=f(0)+11f′′(0)?f′′′(η1),(?1<η1<0)26
14刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
1=f(1)=f(0)+11f′′(0)+f′′′(η2),(?1<η2<0) 26
两式相减,得 f′′′(η1)+f′′′(η2)=6,由f′′′(x)的连续性,知f′′′(x)在闭区间
[η1,η2]上有最大值和最小值,设它们分别为M,m,则有
2m≤[f′′′(η1)+f′′′(η2)]≤2M 或 m≤1?6≤M 2
再由连续函数的介值定理知,至少存在一点ξ∈[η1,η2]?(?1,1),使
f′′′(ξ)=1?6=3 2
【点评】本题是将连续函数的性质用在其三阶导函数上。
2-8 以下四个命题中,正确的是(C)。
(A)若f′(x)在(0,1)内连续,则f(x)在(0,1)内有界。 (B)若f(x)在(0,1)内连续,则f(x)在(0,1)内有界。 (C)若f′(x)在(0,1)内有界,则f(x)在(0,1)内有界。 (D)若f(x)在(0,1)内有界,则f′(x)在(0,1)内有界。
【解析与点评】 考点是:函数的连续性、可导性与有界性。木艾迪考研辅导解:
用排他法。(A),(B) 显然不对,有反例y=1; x
对于(C) , 因f′(x)在(0,1)内有界,即?M>0, 使?x∈(0,1),有
f′(x)≤M。
任取x0,x∈(0,1),则有f(x)=f(x0)+f′(ξ)(x?x0)≤f(x0)+M,
其中f(x0)为有定义的固定值,ξ∈(0,1),这就证明了f(x)在(0,1)内有界。
2-9 设f(x)处处可导,则【 D 】
(A) 当 limf(x)=?∞必有limf′(x)=?∞ x→?∞x→?∞
(B) 当limf′(x)=?∞,必有limf(x)=?∞。 x→?∞x→?∞
(C) 当limf(x)=+∞必有limf′(x)=+∞ x→+∞x→+∞
(D) 当limf′(x)=+∞,必有limf(x)=+∞ x→+∞x→+∞
【解】 (方法一)举反例排除不正确选项.
15刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
令f(x)=x,则limf′(x)=±∞,但f′(x)=1,可见(A)、(C)均不正确.x→±∞
因而只有(D)是正确选项.
(方法二)微分中值定理
若limf′(x)=+∞则存在M>0及x0>0,当x>x0时,f′(x)>M x→+∞
于是当x>x0时,有f(x)?f(x0)=f′(ξ)(x?x0)>M(x?x0)
从而有f(x)>f(x0)+M(x?x0)→+∞(x→+∞) 。
2-10 设f(x)=x(1?x),则 [C]
(A) x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点。
(B) x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点。
(C) x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点。
(D) x=0不是f(x)的极值点,(0,0)也不是曲线y=f(x)的拐点。
【分析】由于f(x)在x=0处的一、二阶导数不存在,可利用f(x)在
x=0的左、右两侧增量(或一阶导数)的符号判断局部极值情况,利用二阶
导数的
符号判断拐点情况。
??x(1?x)x<0?0≤x<1 【解】f(x)=x(1?x)=?x(1?x)
??x(1?x)x≥1?
当x∈(?δ,0)∪(0,δ)(其中0<δ<1)时,f(x)>0,?f(0)>0,而
f(0)=0,所以x=0是f (x)的极小值点。显然,x=0是f(x)的不可导点。
当x ∈ (?δ , 0)时,f(x)=?x(1?x),f′′(x)=2>0,当x ∈ (0 , δ)时,
所以(0 , 0)是曲线y = f (x)的拐点.,故选(C)。 f(x)=x(1?x),f′′(x)=?2<0,
2-11设函数y=f(x)具有二阶导数,且f′(x)>0,f′′(x)>0,?x为自变量x
在x0处的增量,?y与dy分别为f(x)在点x0处对应的增量与微分,若
?x>0,则【 A 】
(B)0<?y<dy。 (C)?y<dy<0。 (D)dy<?y<0。 (A)0<dy<?y。
16刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
【解析与点评】因为 f′(x)>0,则f(x)严格单调增加,f′′(x)>0,则
f(x)为凹,又?x>0,故 0<dy<?y。或直接划草图更为直观。
2-12 (本题满分12分)设e<a<b<e2,证明ln2b?ln2a>
【证】 (方法1)
设?(x)=ln2x?4(b?a).。 2e4lnx41?lnx,则,,所()()x,??='x=2?''x2xx2e2e2
以当x>e时,?''(x)<0,故?'(x)单调减少,从而当e<x<e2时,
442 即当时,?(x)单调增加。 e<x<e?=0,22ee
44因此当e<a<b<e2时, ?(b)>?(a),或 ln2b?2b>ln2a?2a, ee
4故 ln2b?ln2a>2(b?a).。 e?'(x)>?'(e2)=
ln2b?ln2a4(方法2)只需证 >2。 b?ae
对函数ln2x在[a,b]上应用拉格朗日中值定理,得
ln2b?ln2a2lnξ2=, (e<a<ξ<b<e) b?aξ
设?(t)=1?lntlnt,则?'(t)=,当t>e时?'(t)<0,所以?(t)单调减少, tt2
2lne224>2=2,故ln2b?ln2a>2(b?a)。 从而?(ξ)>?(e),即ξeeelnξ2-13 设limx→0f(x)=1,且f′′(x)>0,证明f(x)≥x。 x
【解】 (方法一)移项造辅助函数,利用初值加增减性方法。 由limx→0f(x)=1知 f(0)=0,f′(0)=1,令F(x)=f(x)?x,则F(0)=0, x
F′(0)=0。由于 F′′(x)=f′′(x)>0得到F(x)单调增加,于是
F(x)≥F(0)=0,即f(x)≥x。
(方法二)由limx→0f(x)=1知 f(0)=0,f′(0)=1。 x
利用泰勒公式
17刘坤林编 清华大学东门外 创业大厦1006
知识宝库考研社区()友情提示:购买原版,饮水思源!
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055 x2x2
f(x)=f(0)+f′(0)x+f′′(ξ)=x+f′′(ξ) 22
因为f′′(ξ)>0, 所以f(x)≥x。
(方法三)利用微分中值定理。
由于f′′(x)>0,故f′(x)单调增加,又f(x)?f(0)=xf′(ξ),ξ∈(0,x), 由条件limx→0f(x)=1得到f(0)=0,f′(0)=1 ,故f(x)=xf′(ξ)。 x
若x>0,ξ∈(0,x), f′(ξ)>f′(0)=1,f(x)=xf′(ξ)>x;
若x≤0,ξ∈(x,0),f′(ξ)<f′(0)=1,f(x)=xf′(ξ)≥x。
3.定积分概念与性质综合问题,
3-1 函数f(x)在[0,+∞]上可导,f(0)=1,且满足等式
1xf′(x)+f(x)?f(t)dt=0 x+1∫0
(1) 求导数f′(x);
(2) 证明:当x≥0时,不等式e?x≤f(x)≤1成立.
【提示】(1)用题目给出的等式即可求得。(2)转化成函数的增减性问题求解。
【解】将题设条件改写为 (x+1)f′(x)+(x+1)f(x)?
上式两边对x求导得 (x+1)f′′(x)=?(x+2)f′(x) ∫f(t)dt=0。 0x
即 df′(x)x+2=?dx f′xx+1
两边积分,得 lnf′(x)=?x+ln(x+1)+lnC
在题设等式中令x=0,得f′(0)+f(0)=0
又f(0)=1,于是f′(0)=?1,代入f′(x)的表达式,得C=1,故有
e?x
f′(x)=?。 x+1
(2)(方法一)移项造辅助函数,利用初值加增减性方法。
18刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
当x≥0时,f′(x)<0即f(x)单调减少,又f(0)=1,所以
f(x)≤f(0)=1
设?(x)=f(x)?e
当x≥0时,?x,则?(0)=0,?′(x)=f′(x)+e?x=x?xe。 x+1?′(x)≥0,即?(x)单调增加,而?(x)≥?(0)=0,于是
f(x)≥e?x。 综上所述,当x≥0时,不等式有1≥f(x)≥e?x。
(方法二)用N-L公式,再利用积分的保序性。
因 ∫f′(t)dt=f(x)?f(0)=f(x)?1 0x
?txee?x
代入上式得 f(x)=1?∫dt 将(1)中f′(x)=?01+tx+1
xe?t
又x≥0时, 0≤∫dt≤∫e?tdt=1?e?x 01+t0x
所以 1≥f(x)≥e?x.
x+
x3-2 (本题满分11分)设f(x)=π2∫sintdt,
(I) 证明f(x)是以π为周期的周期函数;
(II) 求f(x)的值域。
【解】 (I)f(x+π)=
π
23x+2x+π∫sintdt,,设t=u+π,则有 x+
xf(x+π)=∫x+xsin(u+π)du=∫π2sinudu=f(x),
故f(x)是以π为周期的周期函数。
(II)分析:将f(x)的值域问题视为[0,π]上的最大最小值问题。
因为sinx在(?∞,+∞)上连续,注意到f(x)的周期为π,故只需在[0,π]的最大最小值问题.先求驻点:
f(x)=sin?x+'?
?π???sinx=cosx?sinx, 2?
19刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
令f′(x)=0,得x1=
3ππ4,x2=3π,且 4?π?f??=∫π4sintdt=2 ?4?4
?3πf??4π?44sint=sintdt=2?, =?∫3π3πsintdt?∫∫π?445π5π
f(0)=∫2sintdt=1,f(π)=∫0π3π2π(?sint)dt=1,
最大值是2,故f(x)的值域是2?因而f(x)的最小值是2?2,3-3 设f(x)在[0,1]上可导,且满足f(1)=2[ 2,2.。]∫1/2
0xf(x)dx,证明存在一点
ξ∈(ξ1,1)?(0,1),使得f(ξ)+ξf'(ξ)=0。
【证】由f(1)=2
使得f(1)=2∫1/20xf(x)dx及积分中值定理知,至少存在一点ξ1∈[0,1/2],∫1/2
0xf(x)dx=ξ1f(ξ1)。在[ξ1,1]上,令F(x)=xf(x),则F(x)
在[ξ1,1]上可导,F(ξ1)=f(1)=F(1)。由罗尔定理知,至少存在一点
ξ∈(ξ1,1)?(0,1),F'(ξ)=f(ξ)+ξf'(ξ)=0。
3-4(本题满分8分)设f(x),g(x)在[a,b]上连续,且满足
∫f(t)dt≥∫g(t)dt,aa
bbxxx∈[a,b),∫f(t)dt=∫g(t)dt, aabb证明: ∫xf(x)dx≤∫xg(x)dx. aa
【证】 ?x∈[a,b]令F(x)=f(x)?g(x),G(x)=
且G(a)=G(b)=0,
∫F(t)dt,则G(x)≥0。axG'(x)=F(x).,从而 b
abbaa∫baxF(x)dx=∫xdG(x)=xG(x)?∫G(x)dx=?∫G(x)dx. ab
由于G(x)≥0,x∈[a,b],故有?
因此 ∫baG(x)dx≤0,即∫xF(x)dx≤0 . ab∫b
axf(x)dx≤∫xg(x)dx. ab
3-5 (本题满分8分) 设f(z),g(x)在[0,1]上的导数连续,且f(0)=0,
f′(x)≥0,g′(x)≥0。证明:对任何a∈[0,1],有
20刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
∫
a0
g(x)f′(x)dx+∫
10
f(x)g′(x)dx≥f(a)g(1)
【解析与点评1】 一个切入点是移项,并将参数易为变量,引入变限积分作为辅助函数,利用导数研究增减性,再由终点值判断函数的正负号,这在水木艾迪考研辅导班刘老师的教学中,是处理等式与不等式证明的一类基本方法,被称为增减性加初值(或终值,本题为终值)的分析法,是重点强调的基本方法,这便是
【证】(方法1)移项造辅助函数,利用初值加增减性方法。 令 F(x)=
x0
10
∫g(t)f′(t)dt+∫
f(t)g′(t)dt?f(x)g(1),x∈[0,1],
则F(x)在[0,1]上的导数连续,并且
F′(x)=g(x)f′(x)?f′(x)g(1)=f′(x)[g(x)?g(1)]。
由于x∈[0,1]时,f′(x)≥0,g′(x)≥0,因此F′(x)≤0,即F(x)在[0,1]上单调递减。 注意到 F(1)=而
10
10
∫g(t)f′(t)dt+∫
10
f(t)g′(t)dt?f(1)g(1),
1
10
∫
10
g(t)f′(t)dt=∫g(t)df(t)=g(t)f(t)0?∫
=f(1)g(1)?
f(t)g′(t)dt
∫
10
f(t)g′(t)dt
故F(1)=0(终值),由终值加增减性的分析法得到x∈[0,1]时,F(x)≥0, 由此令可得x=a∈[0,1]则有∫g(x)f′(x)dx+∫
0a
10
f(x)g′(x)dx≥f(a)g(1)。
【解析与点评2】 由抽象函数的分部积分(另一个切入点),直接利用函数的增减性,再综合考虑积分的比较性质(积分保序性的推论),给出结果。这在水木艾迪考研辅导班刘老师的教学中是处理等式与不等式的又一类基本方法。 (方法2)
a0
a0
a
a0
∫g(x)f′(x)dx=g(x)f(x)0?∫
a0
f(x)g′(x)dx
=f(a)g(a)?∫
10
f(x)g′(x)dx,
∫
g(x)f′(x)dx+∫
f(x)g′(x)dx
a0
=f(a)g(a)?∫
=f(a)g(a)+∫
1a
f(x)g′(x)dx+∫
10
f(x)g′(x)dx
f(x)g′(x)dx
由于x∈[0,1]时,f′(x)≥0,因此f(x)在[0,1]上单调递增,
f(x)≥f(a),x∈[0,1]
又由于x∈[0,1]时,g′(x)≥0,因此
f(x)g′(x)≥f(a)g′(x)≥0,x∈[0,1]
21刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
∫
10f(x)g′(x)dx≥∫1af(a)g′(x)dx=f(a)[g(1)?g(a)], 从而
∫a
0g(x)f′(x)dx+∫10f(x)g′(x)dx
≥f(a)g(a)+f(a)[g(1)?g(a)]=f(a)g(1)
【解析与点评3】本题与水木艾迪考研辅导2005暑期强化班第4讲例22、突破
百分训练营(冲刺班)第2讲例43相雷同,类似例题还有与水木艾迪考研辅导
系列教材《2005考研数学应试导引与进阶》中的例6.52,6.68等典型题目。(刘
坤林、谭泽光等编写,清华大学出版社20xx年7月出版)。
3-6 设a>0,f(x)在[?a,+a]上有二阶连续导数,且f(0)=0,
(1)写出f(x)的带Lagrange余项的一阶麦克劳林公式公式。
(2)证明在[?a,+a]上至少存在一点η,使得
af′′(η)=3∫f(x)dx。 ?a3a
【解】(1)?x∈[?a,a]有
f(x)=f(0)+f′(0)x+
其中ξ在0,x之间。
(2)由上式两边取积分得到 f′′(ξ)2f′′(ξ)2x=f′(0)x+x, 2!2!
∫a
?af(x)dx=∫f(0)xdx+∫?aaa?ax21af′′(ξ)dx=∫x2f′′(ξ)dx, 22?a
由于f′′(x)在[?a,+a]上连续,因此f′′(x)在[?a,+a]上
存在最大最小值m,M,使m≤f′′(x)≤M。
于是由积分估值定理可得到
m∫x2dx≤∫f(x)xdx=0?aaaa1a22′′xfξdx≤Mx()∫0dx, 2∫?a
3即有 m≤3a∫a
?af(x)dx≤M,
对f′′(x)在[?a,+a]上应用连续函数的介值定理,
则在[?a,+a]上至少存在一点η,使得 af′′(η)=33∫a
?af(x)dx.
“M?N”表示“M的充分必3-8 设F(x)是连续函数f(x)的一个原函数,
22刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
要条件是N”,则必有 [A]
(A) F(x)是偶函数?f(x)是奇函数.
(B) F(x)是奇函数?f(x)是偶函数.
(C) F(x)是周期函数?f(x)是周期函数
(D) F(x)是单调函数?f(x)是单调函数.
【解析与点评】 这是基本知识点理解的准确性与基本结论的积累问题。这4分
对水木艾迪考研辅导班的学员真是Dead easy!水木艾迪考研辅导春季基础班
与暑期强化班数学讲义的相关摘录如下:
##
关于原函数的一些重要结论
结论1 连续奇函数之原函数必为偶函数。
结论2 连续偶函数之原函数必为奇函数与常数之和,其中只有一个为奇函数
(C=0)。
结论3 连续周期函数之原函数必为周期函数与线性数之和,且周期不变。
连续周期函数f(x)之原函数为周期函数的充要条件是
∫T
0f(x)dx=0,其中T>0为周期。
结论4 有第一类间断点的函数没有原函数。
结论5 有第二类间断点的函数可以有原函数。
结论6 变限积分表示的函数不一定是原函数。##
注:以上结论在讲课中加以证明,以强化训练。
3-10 下列结论中正确的是( D )。 (A)∫
∫
∫
∫+∞1111dx与∫dx都收敛. 0x(x+1)x(x+1)111dx与∫dx都发散. 0x(x+1)x(x+1)111dx发散,∫dx收敛. 0x(x+1)x(x+1)111dx收敛,∫dx发散. 0x(x+1)x(x+1)(B)+∞1(C)+∞1(D)+∞
1
【解析与点评】 考点是:广义积分收敛性的尺度的运用。正如我们在在水木艾
迪考研辅导教学中强调的那样,当a为奇点时,
∫+∞
af(x)dx=∫f(x)dx+ab∫+∞bf(x)dx为混合型广义积分,前者为第二类广义
23刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
积分,后者为第一类广义积分。分别利用各自的尺度即可判断他们的收敛性。
所谓尺度是:
尺度1:∫+∞
0+∞11或∫0(x?a)p,p>1收敛,p≤1发散。 xp
尺度2:1∫a(x?a)p:p<1收敛,p≥1发散。p≤0为普通定积分。 b
对∫+∞
1111dx,p=2>1,收敛;对∫dx,p=2>1,发散。 0x(x+1)x(x+1)
3-11 广义积分∫+∞
0xdx1= 22(1+x)2【解析与点评】
∫+∞
0xdxd(1+x)111==??2(1+x2)(1+x2)22∫0(1+x2)2+∞2+∞=0+
011= 22
3-12 已知f′(e)=xe
【答】 x?x,且f(1)=0,则f(x)= . 1(lnx)2. 2
lnxlnt, 即 f′(x)=. tx【解】 令ex=t,则x=lnt,于是有f′(t)=
积分得 f(x)=lnx12=(lnx)+C. 利用初始条件f(1)=0, 得∫x2
C=0,
故所求函数为 f(x)=
4.定积分应用问题
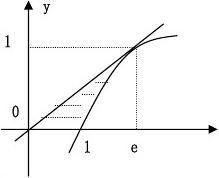
该切线与曲线y=lnx及x轴围成平面4-1 过坐标原点作曲线y=lnx的切线,
图形D.
(1)求D的面积A;
(2)求D绕直线x=e旋转一周所得旋转体的体积V.
【解】设切点的横坐标为x0,则曲线y=lnx在点(x0,lnx0)处的切线方程是
y=lnx0+1(lnx)2. 21(x?x0). x0
24刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
由该切线过原点知 lnx0?1=0,从而x0=e. 所以该切线的方程为y=
平面图形D的面积 A=
(2) 切线y=1x. e∫10(ey?ey)dy=1e?1. 21x与x轴及直线x=e所围成的三角形绕直线x=e旋转e
1所得的圆锥体积为 V1=πe2.曲线y=lnx与x轴及直线x=e所围成的图3
形绕直线x=e旋转所得的旋转体体积为 V2=
因此所求旋转体的体积为 V=V1?V2=∫π(e?e01y2)dy。 121ππe?∫π(e?ey)2dy=(5e2?12e+3).
036
4-2 (本题满分11 点(3,2)是它的一个拐点,直线l1与l2分如图,曲线C的方程为y=f(x),
别是
曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4)。设函数
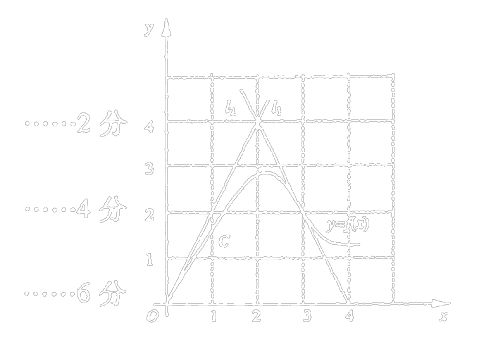
f(x)具有三阶连
续导数,计算定积分∫(x032+x)f′′′(x)dx.
【解析与点评】采用分部积分,注意到拐点必要条件则有
∫3
0′′(x2+x)fm(x)dx=(x2+x)f′′(x)30?∫(2x+1)f(x)dx 0
33
003′=?∫(2x+1)f′′(x)dx =?(2x+1)f′(x)30+2∫f(x)dx
=?[7×(?2)?2]+2∫f′(x)dx 03
=16+2f(x)3
0 =16+4 =20.
25刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
注:本题主要考点是:拐点必要条件与充分条件,含有抽象函数的积分处理,
常用有效方法是分部积分。水木艾迪考研辅导班教学中含有不少此类例题,水
木艾迪考研辅导系列教材《2005考研数学应试导引与进阶》中也有学多这样的
例题和方法,例6.29,例6.32,例6.33,例6.64等,刘坤林等编写,清华大学
出版社20xx年7月出版。
4-3 (本题满分11分) 如图C1,C2分别是y=
点(0,1)的曲线C3是一单调增函数的图象,过1(1+ex)和y=ex的图象,过2
C2上任一点M(x,y)分别做垂直于x轴和y轴
的直线和的直线Lx和Ly,记C1,C2和Lx所围
图形的面积为S1(x),C2,C3和Ly所围图形的
面积为S2(y),如果总有S1(x)=S2(y),求曲
线C3的方程x=

?(y)。
【解析与点评】本题主要考点是:(1)初等函数性质与图象,反函数概念;(2)
用定积分表达面积;(3)变限积分求导数。水木艾迪考研辅导班教学中含有不
少此类例题,可参见基础班综合辅导第2讲例 2.24,例2.25,例2.27,水木艾
迪考研辅导系列教材《2005考研数学应试导引与进阶》中也有许多这样的典型
例题和方法,如例7.7,7.20,7.21等。刘坤林等编写,清华大学出版社2004
年7月出版。 【解】 S1(x)=
yx∫0[et?1(1+et)dt, 2S2(y)=∫[lnt??(t)]dt 1
由题意,1tt[e?(1+e)dt=∫02x∫y
1[lnt??(t)]dt,
为求曲线C3的方程x=?(y),将上式两边对y求导数得到
1dx[ex?(1+ex)]=lny??(y), 2dy
注意到y=e与x=lny的反函数关系,即有 x
11[y?(1+y)]=lny??(y), 2y
26刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055 所以 ?(y)=lny?1111[y?(1+y)]=lny+?。 y22y2
4-4 某建筑工程打地基时,需用汽锤将桩打进土层. 汽锤每次击打,都将克服
土层对桩的阻力而作功. 设土层对桩的阻力的大小与桩被打进地下的深度成正
,汽锤第一次击打将桩打进地下am. 根据设计方案,比(比例系数为k,k>0)
要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数
r(0<r<1). 问
(1) 汽锤击打桩3次后,可将桩打进地下多深?
(2) 若击打次数不限,汽锤至多能将桩打进地下多深?
(注:m表示长度单位米.)
【解】 (1) 设第n次击打后,桩被打进地下xn,第n次击打时,汽锤所作的
功为Wn(n=1,2,3,L). 由题设,当桩被打进地下的深度为x时,土层对桩的阻
力的大小为kx,所以
x1kkW1=∫kxdx=12=a2 022
x2k2k2W2=∫kxdx=x2?x12)=(x2?a2). x122
由W2=rW1可得x2?a=ra,即 x2=(1+r)a.
W3=22222k2k22kxdx=(x?x)=[x3?(1+r)a2]. 32∫x222x3
2从而x3=+r+r2a, 由W3=rW2=r2W1可得 x3?(1+r)a2=r2a2,
即汽锤击打3次后,可将桩打进地下+r+r2am. (2) 由归纳法,设xn=+r+r2+L+rn?1a,则
Wn+1=∫xn+1
xnk22kxdx=xn+1?xn) 2
k2n?1=[xn)a2]. +1?(1+r+L+r2
由于Wn+1=rWn=r2Wn?1=L=rnW1,故得
k2k[xn+1?(1+r+L+rn?1)a2]=rnW1=rna2, 22
27刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
2n?1xn)a2=rna2 +1?(1+r+L+r
从而 xn+11?rn+1=+r+L+ra=a. 1?rn
于是 limxn+1=n→∞11a。即汽锤至多能将桩打进地下am。 1?r1?r
?x=t2+14-5(12分)已知曲线L的方程?(t≥0) 2?y=4t?t
(I)讨论L的凹凸性
(II)过点(?1,0)引L的切线,求切点(x0,y0),并写出切线的方程
(III)求此切线与L(对应x≤x0部分)及x轴所围的平面图形的面积
【解析与点评】(I)
dxdydy4?2t2=2t,=4?2t,==?1 2tdtdtdxtdyd()2dy?1=??2??1=?1<0(t>0处)= ???t2?2tdx2dtt3dt当t≥0时曲线L为凸。
(II)切线方程为?2?y?0=??1?(x+1),切点坐标为?t?
x0=t0+1,y0=4t0?t0,
则4t0?t0=??t?1??(t0+2),4t0?t0=(2?t0)(t0+2) ?0?
得t0+t0?2=0,(t0?1)(t0+2)=0Qt0>0∴t0=1
,切线方程为y=x+1 因此切点(x0,y0)=(2,3)
(III)画出草图,x≥1,t=0时过点(1.0),t=4时过点(5.0),曲线为凸。
(方法1)设L的方程x=g(y)
则S=2222?2?2232∫3
0[(g(y)?(y?1))]dy,t2?4t+y=0,
得x=(2±4?y)2+1
x=2,解出t=2±4?y由于(2,3)在L上,由y=3,x=(2?4?y)2+1=g(y)
28刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
S=∫[(9?y?44?y)?(y?1)]dy 03
=∫(10?2y)dy?4∫03304?ydy
324?yd(4?y)=21+4××(4?y) 30=(10y?y)+4∫02330
=21+2864?=3? 333
S=(方法2)用参数方程面积公式: 3×3191?∫(4t?t2)?2tdt=?∫(8t2?2t3)dt 0220
9817=?+= 2323
3×329817(方法3)S=?∫(4x?1?x+1)dx=?+=。 122323
?e2x,x≤0,4-6 设F(x)=??e?2x,x>0, S表示夹在x轴与曲线y=F(x)之间的面积,对
?
任何t>0,S1(t)表示矩形?t≤x≤t,0≤y≤F(t)的面积。求
(I)S(t)=S?S1(t)的表达式; (II)S(t)的最小值。 【解】 (I) S=2∫+∞
0e?2xdx=?e?2x+∞0=1,
?2t对矩形?t≤x≤t,0≤y≤F(t)的面积,首先应注意F(t)=e
S1(t)=∫F(t)dx=∫e?2tdx=2te?2t ?t?ttt
因此 S(t)=1?2te?2t,t∈(0,+∞).
?2t(II)由于S'(t)=?2(1?2t)e1, 故S(t)的唯一驻点为t=. 2
t<11,S(t)单调减少,t>时S(t)单调增加。 22
所以 S??=1??1?
?2?1为极小值,它也是最小值。 e
?2t(或S′′(t)=8(1?t)e?1?4, S′′??=>0.) ?2?e
4-7(07-3-3)如图,连续函数y=f(x)在敬意[?3,?2],[2,3]上的图形分别是直径为1的上、下半圆周,在区间[?2,0],[0,2]上的图形分别是直径为2的下、上半圆周,设
29刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
F(x)=∫f(t)dt,则下列结论正确的是 0x
(A)F(3)=?35F(?2) (B)F(3)=F(2) 44
53(C)F(?3)=F(2) (D)F(?3)=?F(?2) 44
【解】答案C。首先F(?3)=F(3)。利用积分的几何意义,并注意代数面积的概念(水木艾迪辅导的星级考点)。
F(?3)=∫f(t)dt=?∫f(t)dt 0?30?3
=?(∫
=?(
?2?3f(t)dt+∫f(t)dt) ?20π8?π2=3π3=F(2)=F(3) 424
5.级数的收敛性分析、幂级数展开与求和
5-1 若级数∑an=1∞n收敛,则级数 【 D 】。
(A)∑n=1∞(B)(C)(D)an收敛.∑(?1)an收敛.∑anan+1收敛.∑nn=1n=1∞∞an+an+12n=1∞
收敛.
【解析与点评】【解法1】直接感觉法:首先
知(D)收敛。
【解法2】反例排它法:取反例an=(?1)n∑an=1∞n+1 也收敛,运用运算法则可1
n,可排除(A)(B)(C)。
参见水木艾迪2006考研数学36计例9-2,基础班例8.15,,强化班第6讲
例5,例9等题目。
5-2 设∑a
n=1
n→∞∞n为正项级数,下列结论中正确的是【 B 】。 (A) 若limnan=0,则级数∑a
n=1∞n收敛.
(B) 若存在非零常数λ,使得limnan=λ,则级数n→∞∑an=1∞n发散.
30刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
(C) 若级数∑a
n=1∞n收敛,则limnan=0. n→∞2
(D) 若级数∑a
n=1∞n发散, 则存在非零常数λ,使得limnan=λ. n→∞
【答】应选(B).
∞∞11,则limnan=0,但∑an=∑发散,排除(A),【详解】 取an=→∞nnlnnn=1n=1nlnn
(D); 又取an=1
nn,则级数∑a
n=1∞n收敛,但limnan=∞,排除(C), 故应选(B). n→∞2
5-3(07-3-20,10分)将函数f(x)=
间。 【解】f(x)=1展开成x?1的幂级数,并指出其收敛区2x?3x?4111111) ??=((5?3+(x?1)2+(x?1)5x?4x+1
11111)=?(?=?(+5353?(x?1)2+(x?1)111+? x?12x?11?1+32
11∞(x?1)n11∞(?1)nn=??∑??x?1) ∑nn53n=0352n=02
1∞?2(?1)n?3?n?(x?1)=?∑?n+ n?30n=0?32?
收敛域为x?1<2。
本题考点:幂级数展开,方法是零部件安装法,见水木艾迪考研数学36计之10计,相同例题参见水木艾迪强化班第讲6例20。
5-4(12分) 将函数f(x)=x展开成x的幂级数。 22+x?x
【解析与点评】f(x)=xAB =+(2?x)(1+x)2?x1+x
31刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
A(1+x)+B(2?x)=x令x=2,3A=2,
令A=2 31x=?1,得到3B=?1,B=?,于是 3
f(x)=21111???=?3(2?x)3(1+x)311?? x31?(?x)(1?2
x<1。 1∞1∞xn1∞1?1?nn=∑()?∑(?1)x=∑?n+(?1)n+1?xn,3n=023n=0?n=03?2
参见水木艾迪2006考研数学基础班例9.7, 冲刺班36计例10-4,强化班第1
讲例14等题。 ∞(?1)n1?2x5-5 将函数f(x)=arctan展开成x的幂级数,并求级数∑的和. 2n+11+2xn=0
∞112nn2n【解】 因为f′(x)=?=??xx∈?, 2(1)4,(∑2221+4xn=0
又f(0)=π
4,所以 f(x)=f(0)+∫x
0f′(t)dt=π4?2∫[∑(?1)n4nt2n]dt 0n=0x∞
(?1)n4n
2n+111,x∈(?,). =?2∑422n=02n+1π∞
(?1)n1因为级数∑收敛,函数f(x)在x=处连续,所以 2n=02n+1∞
(?1)n4n
2n+111f(x)=?2∑,x∈(?,]. 422n=02n+1π∞
∞1ππ∞(?1)n(?1)4n11?2n+1=?∑令x=,得f()=?2∑[ +24n42n+12122n=0n=0
∞(?1)nπ1π1=?f(=. 再由f(=0,得 ∑4242n=02n+1
5-6 设有方程xn+nx?1=0,其中n为正整数. 证明此方程存在惟一正实根
αxn,并证明当α>1时,级数∑xn收敛.
n=1∞
【证】记 fn(x)=xn+nx?1. 由fn(0)=?1<0,fn(1)=n>0,及连续
32刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
函数的介值定理知,方程xn+nx?1=0存在正实数根xn∈(0,1).
当x>0时,fn′(x)=nxn?1+n>0,可见fn(x)在[0,+∞)上单调增加, 故方
程xn+nx?1=0存在惟一正实数根xn.
n1?xn1<, 由x+nx?1=0与xn>0知 0<xn=nnn
α故当α>1时,0<xn<()α. ∞1α收敛. 而正项级数∑α收敛,所以当α>1时,级数∑xnnn=1n=1∞1n
5-7 求幂级数?2n1n?1???+(1)1∑?n(2n?1)??x的收敛区间与和函数f(x).
n=1??∞
【解析与点评】本题求解的切入点是级数的加法运算(极限或级数运算法则,
是年年的考点),其次是级数级数展开与求和的解吸运算,即逐项微分与积分,
以及初等函数的麦克劳林级数形式。 [(n+1)(2n+1)+1]x2n+2n(2n?1)2?=x由比率法,lim, 2nn→∞(n+1)(2n+1)[n(2n?1)+1]x
令x2<1,得到级数的收敛半径为1,x2≥1时,原级数发散,收敛区间为
(-1,1)。
记 (?1)n?12nS1(x)=∑x,x∈(?1,1), 2n(2n?1)n=1∞
需两次逐项微分才可化为可求和的幂级数(最终用等比级数求形式)
(?1)n?12n?1S′(x)=∑x,x∈(?1,1),
n=12n?1∞
S′′(x)=∑(?1)n?1x2n?2=
n=1∞1,x∈(?1,1). 1+x2
′(0)=0,再积分两次得到 注意到 S1(0)=0,S1
S1′(x)=∫S1′′(t)dt=∫0x1dt=arctanx, 01+t2 x
x S1(x)=∫S1′(t)dt=∫arctantdt=xarctanx?00x1ln(1+x2). 2
33刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055 级数另一项记为 S2(x)=∑(?1)
n=1∞n?1x2nx2=,x∈(?1,1), 1+x2
所以 f(x)=2S1(x)+S2(x)。
x2
=2xarctanx?ln(1+x)+,x∈(?1,1)。 21+x2
5-8(07-1-20)(本题满分10分)设幂级数∑a
n=0∞nxn在(?∞,+∞)内收敛,其和函数y(x)满足
y′′?2xy′?4y=0,y(0)=0,y′(0)=1。 (Ⅰ)证明an+2=2an,n=1,2,L; n+1
(Ⅱ)求y(x)的表达式。
【证】(1)(方法一)
由y(0)=0得a0=0,y′(0)=1得a1=1,y′′(0)=0=2!a2,a2=0,
y′′′(x)=2xy′′(x)+2y′(x)+4y′(x)=2xy(3?1)(x)+[4+2(3?2)]y(3?2)(x)
y′′′(0)=2y′(0)+4y′(0)=6a1=3!a3,因此a3=1,即k=1时成立ak+2=
y(4)(0)=2y′(0)+[4+2(4?2)]y′′(0)=0=4!a4,a4=0
y(n)(x)=2xy(n?1)(x)+[4+2(n?2)]y(n?2)(x)
假设k≤2n+1时成立: 2ak。 k+1
y(k)(x)=2xy(k?1)(x)+[4+2(k?2)]y(k?2)(x)
y(k)(0)=[4+2(k?2)]y(k?2)(0)
y(2n)(0)=0,y(2n+1)(0)=[4+2(2n?1)]y(2n?1)(0)=(2n+1)!a2n+1
即a2n+1=2a2n?1,且a2n=0。考察k=2n+3的情况, 2n+1?1
y(2n+2)(x)=2xy(2n+1)(x)+[4+2(2n?2)]y(2n)(x),y(2n+2)(0)=0
y(2n+3)(x)=2xy(2n+2)(x)+[4+2(2n?1)]y(2n+1)(x)
y(2n+3)(0)=[4+2(2n+1)]y(2n+1)(0)
=[4+2(2n+1)](2n+1)!a2n+1=(2n+3)!a2n+3
34刘坤林编 清华大学东门外 创业大厦1006
,
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
a2n+3=[4+2(2n+1)](2n+1)!2a2n+1=a2n+1 (2n+3)!2n+3?1
2an,n=1,2,L。 n+1
n?1由归纳法得到 an+2=(方法二)y′=∞∑naxn
n=1
∞, y′′=∑n(n?1)axnn=2n∞∞n?2
代入微分方程得到 ∑(n+1)(n+2)a
n=0n+2x?∑2nanx?∑4anxn=0 nn=1n=0∞
0次幂系数为零:2a2?4a0=0
n次幂系数为零:(n+1)(n+2)an+2?2(n+2)an=0,n=1,2,L
an+2=2an,n=1,2,L n+1
111111a3,a7=a3,a9=a3, 223234(2)a0=0,a1=1,a2=0,a3=1,a5=a2n=0,a2n+1=21a2n?1=L=,n=1,2,L,于是方程的幂级数解为 2nn!
∞n∞∞212n+11y(x)=∑anx=∑=x∑2n=xex
n=0n=0n!n=0n!
本题考点:微分方程解的性质,幂级数逐项微分与求和方法。相同例题参见水木艾迪2007模拟试题二套数三17题。
x4x6x8
5-9 (04-3) 设级数+++L(?∞<x<+∞) 2?42?4?62?4?6?8
的和函数为S(x). 求:
(I) S(x)所满足的一阶微分方程;
(II) S(x)的表达式.
x4x6x8
【解】(I) S(x)=+++L, 2?42?4?62?4?6?8
x3x5x7
易见 S(0)=0,S′(x)=+++L 22?42?4?6
x2x4x6x2
=x(+++L)=x[+S(x)]. 22?42?4?62
35刘坤林编 清华大学东门外 创业大厦1006
水木艾迪考研辅导------20xx年考研解题思路班(微积分) 教务电话:010-62701055
因此S(x)是初值问题 x3
y′=xy+,y(0)=0的解. 2
x3
(II) 方程y′=xy+的通解为 2
xdx y=e∫
[∫xx?∫xdxedx+C] =?2232x2?1+Ce2, 由初始条件y(0)=0,得C=1
故y=?x
22x2+e2?1,因此和函数S(x)=?x
22x2+e2?1.
【点评】考点:幂级数的逐项求导;一阶线形微分方程的求解。
36刘坤林编 清华大学东门外 创业大厦1006
