定义

能够完全重合的两个三角形称为全等三角形。（注：全等三角形是相似三角形中的特殊情况）

当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

由此，可以得出：全等三角形的对应边相等，对应角相等。

(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；

(2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；

(3)有公共边的，公共边一定是对应边；

(4)有公共角的，角一定是对应角；

(5)有对顶角的，对顶角一定是对应角；

三角形全等的判定公理及推论

1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)，这一条也说明了三角形具有稳定性的原因。

2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。

3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。

由3可推到

4、有两角及其一角的对边对应相等的两个三角形全等(AAS或“角角边”)

5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边，直角边”)

所以，SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。

注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。 A是英文角的缩写(angle)，S是英文边的缩写(side)

性质

1、全等三角形的对应角相等、对应边相等。

2、全等三角形的对应边上的高对应相等。

3、全等三角形的对应角平分线相等。

4、全等三角形的对应中线相等。

5、全等三角形面积相等。

6、全等三角形周长相等。

(以上可以简称:全等三角形的对应元素相等)

7、三边对应相等的两个三角形全等。（SSS)

8、两边和它们的夹角对应相等的两个三角形全等。(SAS)

9、两角和它们的夹边对应相等的两个三角形全等。(ASA)

10、两个角和其中一个角的对边对应相等的两个三角形全等。(AAS)

11、斜边和一条直角边对应相等的两个直角三角形全等。(HL)

运用

1、性质中三角形全等是条件，结论是对应角、对应边相等。 而全等的判定却刚好相反。

2、利用性质和判定，学会准确地找出两个全等三角形中的对应边与对应角是关键。在写两个三角形全等时，一定把对应的顶点，角、边的顺序写一致，为找对应边，角提供方便。 3，当图中出现两个以上等边三角形时，应首先考虑用SAS找全等三角形。

4、用在实际中，一般我们用全等三角形测等距离。以及等角，用于工业和军事。有一定帮助。

做题技巧

一般来说考试中线段和角相等需要证明全等。

因此我们可以来采取逆思维的方式。

来想要证全等，则需要什么条件

另一种则要根据题目中给出的已知条件，求出有关信息。

然后把所得的等式运用（AAS/ASA/SAS/SSS/HL）证明三角形全等。

《角平分线》知识总结

1、性质：

角平分线的性质：角平分线上的点到角两边的距离相等。

2、判定：

角平分线的判定：角的内部到角两边距离相等的点在角的平分线上。

3、作图：

角平分线的画法。

4、两个结论：

到三角形三边距离相等的点有四个，其中内部有一个。

如果两个三角形的底边相等，那么它们的面积比就等于它们的高之比；如果两个三角形的高相等，那么它们的面积比就等于它们的底边之比。

5、方法：

证明两个角相等或者两条线段相等，可以通过证明它们所在的两个三角形全等来证明。

在几何解题中，常常需要添加辅助线构造全等三角形，以沟通题设与结论之间的联系。现分类加以说明。

一、延长中线构造全等三角形

例1. 如图1，AD是△ABC的中线，求证：AB＋AC＞2AD。

证明：延长AD至E，使AD＝DE，连接CE。如图2。

∵AD是△ABC的中线，∴BD＝CD。

又∵∠1＝∠2，AD＝DE，

∴△ABD≌△ECD（SAS）。AB＝CE。

∵在△ACE中，CE＋AC＞AE，

∴AB＋AC＞2AD。

二、沿角平分线翻折构造全等三角形

例2. 如图3，在△ABC中，∠1＝∠2，∠ABC＝2∠C。求证：AB＋BD＝AC。

证明：将△ABD沿AD翻折，点B落在AC上的E点处，即：在AC上截取AE＝AB，连接ED。如图4。

∵∠1＝∠2，AD＝AD，AB＝AE，

∴△ABD≌△AED（SAS）。

∴BD＝ED，∠ABC＝∠AED＝2∠C。

而∠AED＝∠C＋∠EDC，

∴∠C＝∠EDC。所以EC＝ED＝BD。

∵AC＝AE＋EC，∴AB＋BD＝AC。

三、作平行线构造全等三角形

例3. 如图5，△ABC中，AB＝AC。E是AB上异于A、B的任意一点，延长AC到D，使CD＝BE，连接DE交BC于F。求证：EF＝FD。

证明：过E作EM∥AC交BC于M，如图6。

则∠EMB＝∠ACB，∠MEF＝∠CDF。

∵AB＝AC，∴∠B＝∠ACB。

∴∠B＝∠EMB。故EM＝BE。

∵BE＝CD，∴EM＝CD。

又∵∠EFM＝∠DFC，∠MEF＝∠CDF，

∴△EFM≌△DFC（AAS）。EF＝FD。

四、作垂线构造全等三角形

例4. 如图7，在△ABC中，∠BAC＝90°，AB＝AC。M是AC边的中点。AD⊥BM交BC于D，交BM于E。求证：∠AMB＝∠DMC。

证明：作CF⊥AC交AD的延长线于F。如图8。

∵∠BAC＝90°，AD⊥BM，

∴∠FAC＝∠ABM＝90°－∠BAE。

∵AB＝AC，∠BAM＝∠ACF＝90°，

∴△ABM≌△CAF（ASA）。

∴∠F＝∠AMB，AM＝CF。

∵AM＝CM，∴CF＝CM。

∵∠MCD＝∠FCD＝45°，CD＝CD，

∴△MCD≌△FCD（SAS）。所以∠F＝∠DMC。

∴∠AMB＝∠F＝∠DMC。

五、沿高线翻折构造全等三角形

例5. 如图9，在△ABC中，AD⊥BC于D，∠BAD＞∠CAD。求证：AB＞AC。

证明：把△ADC沿高AD翻折，点C落在线段DB上的E点处，即：在DB上截取DE＝DC，连接AE。如图10。

∴△ADC≌△ADE（SAS）。AC＝AE，∠C＝∠AED。

∵∠AED＞∠B，∴∠C＞∠B。从而AB＞AC。

六、绕点旋转构造全等三角形

例6. 如图11，正方形ABCD中，∠1＝∠2，Q在DC上，P在BC上。求证：PA＝PB＋DQ。

证明：将△ADQ绕点A按顺时针方向旋转90°，使AD与AB重合，得到△ABM，即：延长CB到M，使BM＝DQ，连接AM。如图12。

∴△ABM≌△ADQ（SAS）。

∴∠4＝∠2＝∠1，∠M＝∠AQD。

∵AB∥CD，∴∠AQD＝∠BAQ＝∠1＋∠3＝∠4＋∠3＝∠MAP。

∴∠M＝∠MAP。

∴PA＝PM＝PB＋BM＝PB＋DQ（因BM＝DQ）。

第二篇：三角形知识点总结

第一章    图形的初步认识

考点一、线段垂直平分线，角的平分线，垂线

1、线段垂直平分线的性质定理及逆定理

垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线。

线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等。

逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

2、角的平分线及其性质

一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

角的平分线有下面的性质定理：

（1）角平分线上的点到这个角的两边的距离相等。

（2）到一个角的两边距离相等的点在这个角的平分线上。

3垂线的性质：

性质1：过一点有且只有一条直线与已知直线垂直。

性质2：直线外一点与直线上各点连接的所有线段中，垂线段最短。简称：垂线段最短。

考点二、平行线   

    1、平行线的概念

在同一个平面内，不相交的两条直线叫做平行线。同一平面内，两条直线的位置关系只有两种：相交或平行。

4、平行线的性质

（1）两直线平行，同位角相等；（2）两直线平行，内错角相等；（3）两直线平行，同旁内角互补。

考点三、投影与视图  

    1、投影

投影的定义：用光线照射物体，在地面上或墙壁上得到的影子，叫做物体的投影。

平行投影：由平行光线（如太阳光线）形成的投影称为平行投影。

中心投影：由同一点发出的光线所形成的投影称为中心投影。

2、视图

当我们从某一角度观察一个实物时，所看到的图像叫做物体的一个视图。物体的三视图特指主视图、俯视图、左视图。

主视图：在正面内得到的由前向后观察物体的视图，叫做主视图。

俯视图：在水平面内得到的由上向下观察物体的视图，叫做俯视图。

左视图：在侧面内得到的由左向右观察物体的视图，叫做左视图，有时也叫做侧视图。

第二章    三角形

考点一、三角形

1、三角形的分类

三角形按边的关系分类如下：

         不等边三角形

三角形                   底和腰不相等的等腰三角形

         等腰三角形

                         等边三角形

三角形按角的关系分类如下：

         直角三角形（有一个角为直角的三角形）

三角形                锐角三角形（三个角都是锐角的三角形）

         斜三角形

                      钝角三角形（有一个角为钝角的三角形）

把边和角联系在一起，我们又有一种特殊的三角形：等腰直角三角形。它是两条直角边相等的直角三角形。

2、三角形的三边关系定理及推论

（1）三角形三边关系定理：三角形的两边之和大于第三边。

推论：三角形的两边之差小于第三边。

3、三角形的内角和定理及推论

三角形的内角和定理：三角形三个内角和等于180°。

推论：

①直角三角形的两个锐角互余。

②三角形的一个外角等于和它不相邻的来两个内角的和。

③三角形的一个外角大于任何一个和它不相邻的内角。

注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角。

4、三角形的面积

三角形的面积=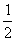×底×高

考点二、全等三角形   

    1、全等三角形的概念

能够完全重合的两个三角形叫做全等三角形。。

2、三角形全等的判定

三角形全等的判定定理：

（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）

（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）

（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）。

直角三角形全等的判定：

对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）

3、全等变换

只改变图形的位置，不改变其形状大小的图形变换叫做全等变换。

全等变换包括一下三种：

（1）平移变换：把图形沿某条直线平行移动的变换叫做平移变换。

（2）对称变换：将图形沿某直线翻折180°，这种变换叫做对称变换。

（3）旋转变换：将图形绕某点旋转一定的角度到另一个位置，这种变换叫做旋转变换。

考点三、等腰三角形   

    1、等腰三角形的性质

（1）等腰三角形的性质定理及推论：

定理：等腰三角形的两个底角相等（简称：等边对等角）

推论1：等腰三角形顶角平分线平分底边并且垂直于底边。即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。

推论2：等边三角形的各个角都相等，并且每个角都等于60°。

2、三角形中的中位线

连接三角形两边中点的线段叫做三角形的中位线。

（1）三角形共有三条中位线，并且它们又重新构成一个新的三角形。

（2）要会区别三角形中线与中位线。

三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。

三角形中位线定理的作用：

位置关系：可以证明两条直线平行。

数量关系：可以证明线段的倍分关系。

常用结论：任一个三角形都有三条中位线，由此有：

结论1：三条中位线组成一个三角形，其周长为原三角形周长的一半。

结论2：三条中位线将原三角形分割成四个全等的三角形。

结论3：三条中位线将原三角形划分出三个面积相等的平行四边形。

结论4：三角形一条中线和与它相交的中位线互相平分。

结论5：三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。

第三章    解直角三角形

考点一、直角三角形的性质   

    1、直角三角形的两个锐角互余

2、在直角三角形中，30°角所对的直角边等于斜边的一半。

3、直角三角形斜边上的中线等于斜边的一半

 4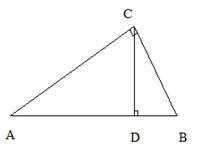直角三角形两直角边a，b的平方和等于斜边c的平方，即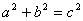

5、摄影定理

在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项

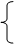
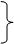∠ACB=90°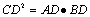       

  

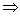
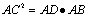
CD⊥AB           

6、常用关系式

由三角形面积公式可得：

ABCD=ACBC

考点二、锐角三角函数的概念    （3~8分）

    1、如图，在△ABC中，∠C=90°

①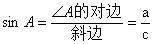

②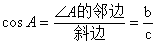

③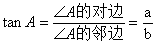

④

2、一些特殊角的三角函数值

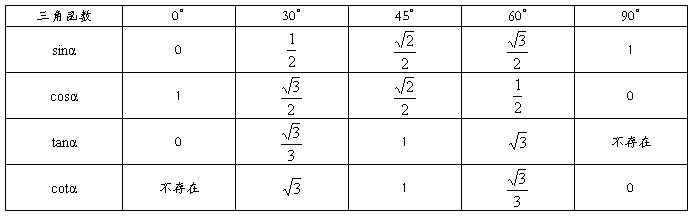
3、各锐角三角函数之间的关系

（1）互余关系：sinA=cos(90°—A)，cosA=sin(90°—A)，tanA=cot(90°—A)，cotA=tan(90°—A)

（2）平方关系：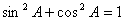

（3）倒数关系：tanAtan(90°—A)=1

（4）弦切关系：tanA=

第四章     图形的相似

考点一、比例线段   

1、比例的性质

（1）基本性质

①a：b=c：d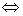ad=bc

②a：b=b：c

（2）更比性质（交换比例的内项或外项）

              （交换内项）

    （交换外项）

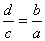             （同时交换内项和外项）

（3）反比性质（交换比的前项、后项）：

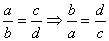
（4）合比性质：

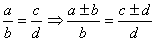
（5）等比性质：

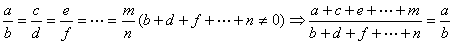
3、黄金分割

把线段AB分成两条线段AC，BC（AC>BC），并且使AC是AB和BC的比例中项，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC=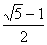AB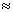0.618AB

考点二、平行线分线段成比例定理 

三条平行线截两条直线，所得的对应线段成比例。

考点三、相似三角形   

    1、相似三角形的概念

对应角相等，对应边成比例的三角形叫做相似三角形。相似用符号“∽”来表示

2、相似三角形的基本定理

平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。

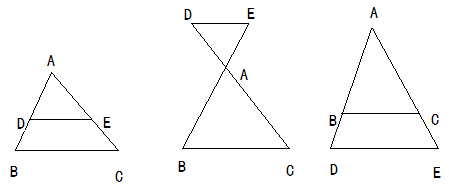
相似三角形的等价关系：

（1）反身性：对于任一△ABC，都有△ABC∽△ABC；

（2）对称性：若△ABC∽△A’B’C’，则△A’B’C’∽△ABC

（3）传递性：若△ABC∽△A’B’C’，并且△A’B’C’∽△A’’B’’C’’，则△ABC∽△A’’B’’C’’。

3、三角形相似的判定

（1）三角形相似的判定方法

①定义法：对应角相等，对应边成比例的两个三角形相似

②平行法：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似

③判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似，可简述为两角对应相等，两三角形相似。

④判定定理2：如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似，可简述为两边对应成比例且夹角相等，两三角形相似。

⑤判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似，可简述为三边对应成比例，两三角形相似

（2）直角三角形相似的判定方法

①以上各种判定方法均适用

②定理：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似

4、相似三角形的性质

（1）相似三角形的对应角相等，对应边成比例

（2）相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比

（3）相似三角形周长的比等于相似比

（4）相似三角形面积的比等于相似比的平方。

5、相似多边形

（1）如果两个边数相同的多边形的对应角相等，对应边成比例，那么这两个多边形叫做相似多边形。相似多边形对应边的比叫做相似比（或相似系数）

（2）相似多边形的性质

①相似多边形的对应角相等，对应边成比例

②相似多边形周长的比、对应对角线的比都等于相似比

③相似多边形中的对应三角形相似，相似比等于相似多边形的相似比

④相似多边形面积的比等于相似比的平方

6、位似图形

如果两个图形不仅是相似图形，而且每组对应点所在直线都经过同一个点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，此时的相似比叫做位似比。

性质：每一组对应点和位似中心在同一直线上，它们到位似中心的距离之比都等于位似比。

由一个图形得到它的位似图形的变换叫做位似变换。利用位似变换可以把一个图形放大或缩小。