椭圆知识点
1.椭圆的定义 ,动点
,动点 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.注意:若
的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.注意:若 ,则动点
,则动点 的轨迹为线段
的轨迹为线段 ;
;
若 ,则动点
,则动点 的轨迹无图形.
的轨迹无图形.
2椭圆的标准方程
注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;2.在椭圆的两种标准方程中,都有 和
和 ; 3.椭圆的焦点总在长轴上.
; 3.椭圆的焦点总在长轴上.
3.椭圆的简单几何性质
(1)对称性:(2)范围: ,
, 。
。
(3)顶点:  ,
, ,
, ,
, 其中长轴长为2
其中长轴长为2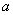 ,短轴长为2
,短轴长为2 ;(4)准线:两条准线
;(4)准线:两条准线 ; ⑤离心率:
; ⑤离心率: ,椭圆
,椭圆
 ,
, 越小,椭圆越圆;
越小,椭圆越圆; 越大,椭圆越扁。⑥通径
越大,椭圆越扁。⑥通径 4:椭圆
4:椭圆 与
与 
 的区别和联系
的区别和联系

4.焦点三角形(椭圆上的一点与两焦点所构成的三角形): ,当
,当 即
即 为短轴端点时,
为短轴端点时, 的最大值为bc;
的最大值为bc;
5、圆锥曲线的中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解。在椭圆 中,以
中,以 为中点的弦所在直线的斜率k=-
为中点的弦所在直线的斜率k=- ;
;
6、弦长公式:若直线 与圆锥曲线相交于两点A、B,且
与圆锥曲线相交于两点A、B,且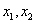 分别为A、B的横坐标,则
分别为A、B的横坐标,则 =
= ,若
,若 分别为A、B的纵坐标,则
分别为A、B的纵坐标,则 =
= 特别提醒:因为
特别提醒:因为 是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验
是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验 !
!
7.直线与圆锥曲线的位置关系:
(1)相交:
 直线与椭圆相交;(2)相切:
直线与椭圆相交;(2)相切:
 直线与椭圆相切; (3)相离:
直线与椭圆相切; (3)相离:
 直线与椭圆相离;
直线与椭圆相离;
注意.
1.判断曲线关于 轴、
轴、 轴、原点对称的依据:
轴、原点对称的依据:
① 若把曲线方程中的 换成
换成 ,方程不变,则曲线关于
,方程不变,则曲线关于 轴对称;
轴对称;
② 若把曲线方程中的 换成
换成 ,方程不变,则曲线关于
,方程不变,则曲线关于 轴对称;
轴对称;
③ 若把曲线方程中 、
、 同时换成
同时换成 、
、 ,方程不变,则曲线关于原点对称。
,方程不变,则曲线关于原点对称。
2.点与椭圆的位置关系:(1)点 在椭圆外
在椭圆外
 ;
;
(2)点 在椭圆上
在椭圆上
 =1;(3)点
=1;(3)点 在椭圆内
在椭圆内

3 因为 ,所以
,所以 的取值范围是
的取值范围是 。
。 越接近1,则
越接近1,则 就越接近
就越接近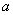 ,从而
,从而 越小,因此椭圆越扁;反之,
越小,因此椭圆越扁;反之, 越接近于0,
越接近于0, 就越接近0,从而
就越接近0,从而 越接近于
越接近于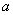 ,这时椭圆就越接近于圆。
,这时椭圆就越接近于圆。
题型1:椭圆定义的运用
[例1 ] 在 中,
中, .若以
.若以 为焦点的椭圆经过点
为焦点的椭圆经过点 ,则该椭圆的离心率
,则该椭圆的离心率 .
.
题型2 求椭圆的标准方程
[例2 ]设椭圆的中心在原点,坐标轴为对称轴,一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上较近的端点距离为 -4,求此椭圆方程.
-4,求此椭圆方程.
 [例3 ] 椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是
[例3 ] 椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是 ,求这个椭圆方程.
,求这个椭圆方程.
题型3:椭圆的几何性质的运用
4. 如图所示,椭圆中心在原点,F是左焦点,直线 与BF交于D,且
与BF交于D,且 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A  B
B  C
C  D
D 
题型4:椭圆的最值问题
[例5 ]椭圆 上的点到直线l:
上的点到直线l: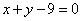 的距离的最小值为___________.
的距离的最小值为___________.
6.  是椭圆
是椭圆 上一点,
上一点, 、
、 是椭圆的两个焦点,求
是椭圆的两个焦点,求 的最大
的最大
7.已知点 是椭圆
是椭圆 上的在第一象限内的点,又
上的在第一象限内的点,又 、
、 ,
,
 是原点,则四边形
是原点,则四边形 的面积的最大值是_________.
的面积的最大值是_________.
考点4 椭圆与向量、解三角形的交汇问题
[例8 ] 已知椭圆 的中心为坐标原点
的中心为坐标原点 ,一个长轴端点为
,一个长轴端点为 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)求m的取值范围.
9 如图,在Rt△ABC中,∠CAB=90°,AB=2,AC= 。一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变,直线l经过A与曲线E交于M、N两点。
。一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变,直线l经过A与曲线E交于M、N两点。
(1)建立适当的坐标系,求曲线E的方程;
(2)设直线l的斜率为k,若∠MBN为钝角,求k的取值范围。
 10在平面直角坐标系
10在平面直角坐标系 中,如图,已知椭圆
中,如图,已知椭圆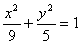 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T( )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M 、
、 ,其中m>0,
,其中m>0, 。(1)设动点P满足
。(1)设动点P满足 ,求点P的轨迹;
,求点P的轨迹;
(2)设 ,求点T的坐标;
,求点T的坐标;
(3)设 ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
圆锥曲线的性质总结
1 若 在椭圆
在椭圆 上,则过
上,则过 的椭圆的切线方程是
的椭圆的切线方程是 .
.
2 椭圆 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点
(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为 .
.
3 椭圆 (a>b>0)的焦半径公式:
(a>b>0)的焦半径公式:
 ,
, (
( ,
, 
 ).
).
4 AB是椭圆 的不平行于对称轴的弦,M
的不平行于对称轴的弦,M 为AB的中点,则
为AB的中点,则 ,
,
5 已知椭圆方程为 左右两焦点分别为
左右两焦点分别为 设焦点三角形
设焦点三角形 ,若
,若 最大,则点P为椭圆短轴的端点。
最大,则点P为椭圆短轴的端点。
6 若 在双曲线
在双曲线 (a>0,b>0)上,则过
(a>0,b>0)上,则过 的双曲线的切线方程是
的双曲线的切线方程是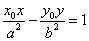 .
.
7 双曲线 (a>0,b>o)的焦半径公式:(
(a>0,b>o)的焦半径公式:( ,
, 
当 在右支上时,
在右支上时, ,
, .
.
当 在左支上时,
在左支上时, ,
,
8 椭圆 上一P(除
上一P(除 、
、 )与长轴的端点
)与长轴的端点 、
、 的连线
的连线 斜率的积是
斜率的积是 (焦点在y轴时
(焦点在y轴时 )
)
9 已知椭圆方程为 两焦点分别为
两焦点分别为 设焦点三角形
设焦点三角形 中
中 则
则
10 设P点是双曲线 (a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记
(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记 ,则(1)
,则(1) .(2)
.(2)  .
.
11 过椭圆 (a>0, b>0)上任一点
(a>0, b>0)上任一点 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且 (常数).
(常数).
12 若 在椭圆
在椭圆 上,则过
上,则过 的椭圆的切线方程是
的椭圆的切线方程是 .
.
13 已知椭圆 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且
(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且 .(1)
.(1)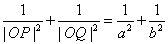 ;(2)(3)
;(2)(3) 的最小值是
的最小值是 .
.
14  为椭圆
为椭圆 上一点,过点
上一点,过点 作斜率互为相反数的两条直线
作斜率互为相反数的两条直线 、
、 ,分别交椭圆于
,分别交椭圆于 、
、 两点。求证直线
两点。求证直线 的斜率为定值
的斜率为定值
15 设P点是椭圆 ( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记
( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记 ,则(1)
,则(1) .(2)
.(2)  .
.
17 若 是过抛物线
是过抛物线 的焦点
的焦点 的弦。设
的弦。设
 ,则(1)
,则(1) ;(2)
;(2) 。(2)
。(2) (3)设直线
(3)设直线 的倾斜角为
的倾斜角为 ,则
,则 。
。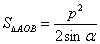 (4)若
(4)若 是过抛物线
是过抛物线 的焦点
的焦点 的弦,则以
的弦,则以 为直径的圆与抛物线的准线相切。(5)
为直径的圆与抛物线的准线相切。(5)
18 若抛物线方程为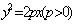 ,过(
,过( ,0)的直线与之交于A、B两点,则OA⊥OB。反之也成立。
,0)的直线与之交于A、B两点,则OA⊥OB。反之也成立。
第二篇:椭圆知识点小结
椭圆知识点
知识要点小结:知识点一:
椭圆的定义
平面内一个动点 到两个定点
到两个定点 、
、 的距离之和等于常数
的距离之和等于常数 ,这个动点
,这个动点 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.
的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距.
注意:若 ,则动点
,则动点 的轨迹为线段
的轨迹为线段 ;
;
若 ,则动点
,则动点 的轨迹无图形.
的轨迹无图形.
知识点二:椭圆的标准方程
1.当焦点在 轴上时,椭圆的标准方程:
轴上时,椭圆的标准方程:
 ,其中
,其中
2.当焦点在 轴上时,椭圆的标准方程:
轴上时,椭圆的标准方程:
 ,其中
,其中 ;注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;
;注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;
2.在椭圆的两种标准方程中,都有 和
和 ;
;
3.椭圆的焦点总在长轴上.
当焦点在 轴上时,椭圆的焦点坐标为
轴上时,椭圆的焦点坐标为 ,
, ;
;
当焦点在 轴上时,椭圆的焦点坐标为
轴上时,椭圆的焦点坐标为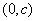 ,
,
 知识点三:椭圆的简单几何性质
知识点三:椭圆的简单几何性质
椭圆:
 的简单几何性质
的简单几何性质
(1)对称性:对于椭圆标准方程
 :说明:把
:说明:把 换成
换成 、或把
、或把 换成
换成 、或把
、或把 、
、 同时换成
同时换成 、
、 、原方程都不变,所以椭圆
、原方程都不变,所以椭圆 是以
是以 轴、
轴、 轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
(2)范围:
椭圆上所有的点都位于直线 和
和 所围成的矩形内,所以椭圆上点的坐标满足
所围成的矩形内,所以椭圆上点的坐标满足 ,
, 。
。
(3)顶点:①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
②椭圆
 与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为
与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为  ,
, ,
, ,
,
③线段 ,
, 分别叫做椭圆的长轴和短轴,
分别叫做椭圆的长轴和短轴, ,
, 。
。 和
和 分别叫做椭圆的长半轴长和短半轴长。
分别叫做椭圆的长半轴长和短半轴长。
 (4)离心率:
(4)离心率:
①椭圆的焦距与长轴长度的比叫做椭圆的离心率,用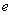 表示,记作
表示,记作 。
。
②因为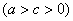 ,所以
,所以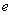 的取值范围是
的取值范围是 。
。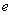 越接近1,则
越接近1,则 就越接近
就越接近 ,从而
,从而 越小,因此椭圆越扁;反之,
越小,因此椭圆越扁;反之,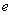 越接近于0,
越接近于0, 就越接近0,从而
就越接近0,从而 越接近于
越接近于 ,这时椭圆就越接近于圆。 当且仅当
,这时椭圆就越接近于圆。 当且仅当 时,
时, ,这时两个焦点重合,图形变为圆,方程为
,这时两个焦点重合,图形变为圆,方程为 。注意: 椭圆
。注意: 椭圆 的图像中线段的几何特征(如下图):(1)
的图像中线段的几何特征(如下图):(1) ;
;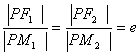 ;
; ;
;
(2) ;
; ;
; ;
;
(3) ;
; ;
; ;
;
知识点四:椭圆 与
与 
 的区别和联系
的区别和联系

注意:椭圆 ,
,
 的相同点:形状、大小都相同;参数间的关系都有
的相同点:形状、大小都相同;参数间的关系都有 和
和 ,
, ;不同点:两种椭圆的位置不同;它们的焦点坐标也不相同。
;不同点:两种椭圆的位置不同;它们的焦点坐标也不相同。
规律方法:
1.如何确定椭圆的标准方程?
任何椭圆都有一个对称中心,两条对称轴。当且仅当椭圆的对称中心在坐标原点,对称轴是坐标轴,椭圆的方程才是标准方程形式。此时,椭圆焦点在坐标轴上。
确定一个椭圆的标准方程需要三个条件:两个定形条件 ;一个定位条件焦点坐标,由焦点坐标的形式确定标准方程的类型。
;一个定位条件焦点坐标,由焦点坐标的形式确定标准方程的类型。
2.椭圆标准方程中的三个量 的几何意义
的几何意义
椭圆标准方程中, 三个量的大小与坐标系无关,是由椭圆本身的形状大小所确定的。分别表示椭圆的长半轴长、短半轴长和半焦距长,均为正数,且三个量的大小关系为:
三个量的大小与坐标系无关,是由椭圆本身的形状大小所确定的。分别表示椭圆的长半轴长、短半轴长和半焦距长,均为正数,且三个量的大小关系为: ,
,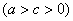 ,且
,且 。
。
 可借助右图理解记忆:
可借助右图理解记忆:
显然: 恰构成一个直角三角形的三条边,其中a是斜边,b、c为两条直角边。
恰构成一个直角三角形的三条边,其中a是斜边,b、c为两条直角边。
3.如何由椭圆标准方程判断焦点位置
椭圆的焦点总在长轴上,因此已知标准方程,判断焦点位置的方法是:看 ,
, 的分母的大小,哪个分母大,焦点就在哪个坐标轴上。
的分母的大小,哪个分母大,焦点就在哪个坐标轴上。
4.方程 是表示椭圆的条件
是表示椭圆的条件
方程 可化为
可化为 ,即
,即 ,所以只有A、B、C同号,且A
,所以只有A、B、C同号,且A B时,方程表示椭圆。当
B时,方程表示椭圆。当 时,椭圆的焦点在
时,椭圆的焦点在 轴上;当
轴上;当 时,椭圆的焦点在
时,椭圆的焦点在 轴上。
轴上。
5.求椭圆标准方程的常用方法:
①待定系数法:由已知条件确定焦点的位置,从而确定椭圆方程的类型,设出标准方程,再由条件确定方程中的参数 的值。其主要步骤是“先定型,再定量”;
的值。其主要步骤是“先定型,再定量”;
②定义法:由已知条件判断出动点的轨迹是什么图形,然后再根据定义确定方程。
6.共焦点的椭圆标准方程形式上的差异
共焦点,则c相同。与椭圆
 共焦点的椭圆方程可设为
共焦点的椭圆方程可设为
 ,此类问题常用待定系数法求解。
,此类问题常用待定系数法求解。
7.判断曲线关于 轴、
轴、 轴、原点对称的依据:
轴、原点对称的依据:
① 若把曲线方程中的 换成
换成 ,方程不变,则曲线关于
,方程不变,则曲线关于 轴对称;
轴对称;
② 若把曲线方程中的 换成
换成 ,方程不变,则曲线关于
,方程不变,则曲线关于 轴对称;
轴对称;
③ 若把曲线方程中的 、
、 同时换成
同时换成 、
、 ,方程不变,则曲线关于原点对称。
,方程不变,则曲线关于原点对称。
8.如何求解与焦点三角形△PF1F2(P为椭圆上的点)有关的计算问题?
思路分析:与焦点三角形△PF1F2有关的计算问题时,常考虑到用椭圆的定义及余弦定理(或勾股定理)、三角形面积公式 相结合的方法进行计算解题。
相结合的方法进行计算解题。
将有关线段 ,有关角
,有关角 (
(

 )结合起来,建立
)结合起来,建立 、
、 之间的关系.
之间的关系.
9.如何计算椭圆的扁圆程度与离心率的关系?
长轴与短轴的长短关系决定椭圆形状的变化。离心率 ,因为
,因为 ,
, ,用
,用 表示为
表示为 。
。
显然:当 越小时,
越小时, 越大,椭圆形状越扁;当
越大,椭圆形状越扁;当 越大,
越大, 越小,椭圆形状越趋近于圆。
越小,椭圆形状越趋近于圆。
