华北电力大学科技学院
实 验 报 告
实验名称 矩阵连乘问题
课程名称 计算机算法设计与分析
专业班级:软件12K1 学生姓名:吴旭
学 号: 121909020124 成 绩:
…… …… 余下全文
实验名称 矩阵连乘问题
课程名称 计算机算法设计与分析
专业班级:软件12K1 学生姓名:吴旭
学 号: 121909020124 成 绩:
…… …… 余下全文
王典 学号Y201005009
矩阵连乘_实验报告
一、设计分析
? 问题描述:
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
? 设计思路:
设X=(x1,...xm), Y=(y1,y2,...yn)是两个序列,Z=(z1,z2,...zk)是X与Y的LCS。下列结论成立:
⑴ 如xm=yn, 则zk=xm=yn, Zk-1是Xm-1和Yn-1的LCS,即,
LCSXY=LCSXm-1Yn-1+<xm=yn>.
⑵ 若xm≠yn,且zk≠xm,则Z是Xm-1和Y的LCS,即
LCSXY=LCSXm-1Y
⑶ 若xm≠yn,且zk≠yn,则Z是X与Yn-1的LCS,即
LCSXY=LCSXYn-1
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此,最长公共子序列问题具有最优子结构性质。
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列xi和yj的最长公共子序列的长度。其中, Xi={x1,x2,…xi};Yj={y1,y2,…,yj}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下:
?0
?c[i][j]??c[i?1][j?1]?1
?max?c[i][j?1],c[i?1][j]??i?0,j?0i,j?0;xi?yji,j?0;xi?yj
复杂度分析
算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。
程序代码
c语言实现
1

2
王典 学号Y201005009
三、测试用例
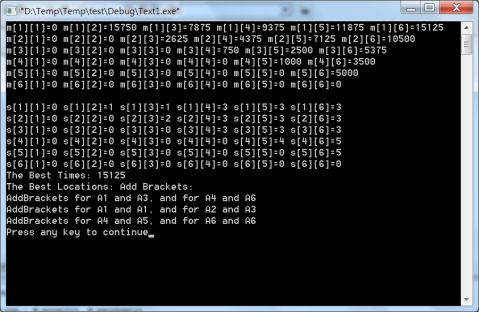
四、实验总结
通过本实验加深了对动态规划算法的理解,总结出动态规划算法的一般步骤:
…… …… 余下全文
攀枝花学院实验报告
实验课程:计算机算法实验 实验项目:矩阵连乘 实验日期:2013.4.9
系:数学与计算机学院 班级:软件工程 姓名:冯斌 学号:201010804004
指导教师:银星 成绩:
…… …… 余下全文
矩阵连乘_实验报告
一、设计分析
l 问题描述:
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
l 设计思路:
设X=(x1,...xm), Y=(y1,y2,...yn)是两个序列,Z=(z1,z2,...zk)是X与Y的LCS。下列结论成立:
⑴ 如xm=yn, 则zk=xm=yn, Zk-1是Xm-1和Yn-1的LCS,即,
LCSXY=LCSXm-1Yn-1+<xm=yn>.
⑵ 若xm≠yn,且zk≠xm,则Z是Xm-1和Y的LCS,即
LCSXY=LCSXm-1Y
⑶ 若xm≠yn,且zk≠yn,则Z是X与Yn-1的LCS,即
LCSXY=LCSXYn-1
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此,最长公共子序列问题具有最优子结构性质。
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列xi和yj的最长公共子序列的长度。其中, Xi={x1,x2,…xi};Yj={y1,y2,…,yj}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下:
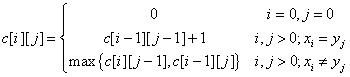
复杂度分析
算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。
程序代码
c语言实现

三、测试用例

四、实验总结
通过本实验加深了对动态规划算法的理解,总结出动态规划算法的一般步骤:
1、找出最优解的性质,并刻划其结构特征。
2、递归地定义最优值。
…… …… 余下全文
南京信息工程大学 实验(实习)报告
院 计算机与软件学院 专业 软件工程 年级 2013 班次3 姓名 魏开阳 学号 20131344105
一、 实验内容
矩阵连乘问题,给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2,3…,n-1。考察这n个矩阵的连乘A1,A2,…,An。
二、 主要思想
由于矩阵乘法满足结合律,故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已经完全加括号,则可依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。完全加括号的矩阵连乘积可递归的定义为:
(1) 单个矩阵是完全加括号的;
(2) 矩阵连乘积A是完全加括号的,则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号,即A=(BC)。
运用动态规划法解矩阵连乘积的最优计算次序问题。按以下几个步骤进行
1、 分析最优解的结构
设计求解具体问题的动态规划算法的第1步是刻画该问题的最优解的结构特征。为方便起见,将矩阵连乘积简记为A[i:j]。考察计算A[1:n]的最优计算次序。设这个计算次序矩阵在Ak和Ak+1之间将矩阵链断开,,则其相应的完全加括号方式为((A1…Ak)(Ak+1…An))。依此次序,先计算A[1:k]和A[k+1:n],然后将计算结果相乘得到A[1:n]。
…… …… 余下全文
实验一、矩阵连乘问题
问题描述与实验目的:
给定n个矩阵A1,A2,?,An,其中,Ai与Aj+1是可乘的,i=1,2,?,n-l。
你的任务是要确定矩阵连乘的运算次序,使计算这n个矩阵的连乘积A1A2?An时总的元素乘法次数达到最少。
例如:3个矩阵A1,A2,A3,阶分别为10×100、100×5、5×50,计算连乘积A1A2A3时按(A1A2)A3所需的元素乘法次数达到最少,为7500次。 输入
测试数据有若干组,每组测试数据有2行。
每组测试数据的第1行是一个整数n,(0<n<20),第2行是n+1个正整数p0、p1、p2、?、pn,这些整数不超过100,相邻两个整数之间空一格,他们表示n
个矩阵A1,A2,?,An,的阶pi-1?pi,i=1,2,?,n。
输入直到文件结束。
输出
对输入中的每组测试数据,输出2行。先在一行上输出“Case #”,其中“#”是测试数据的组号(从1开始),再在第2行上输出计算这n个矩阵的连乘积A1A2?An时最少的总的元素乘法次数,再空一格,接着在同一行上输出矩阵连乘的添括号形式。
注意:最外层括号应去掉。
实验结果:
输入样例
3
10 100 5 50
4
50 10 40 30 5
输出样例
Case 1
7500 (A1A2)A3
Case 2
10500 A1(A2(A3A4))
实验报告要求:
1.先分析要点、写出动态方程
2.提供能正确运行的程序。要有一般性,即可同时处理若干组数据,每组2行。
3.设计、调试中的问题及实验体会。
…… …… 余下全文
实验目的:1.矩阵相乘
实验内容:给定两个矩阵A和B,其中A是具有M行、K列的矩阵,B为K行、N列矩阵,A和B的矩阵积为C,C为M行,N列。矩阵C中第i行、第j列的元素Ci,j就是矩阵A第i行每个元素和矩阵B第j列每个元素乘积的和。本实验的目的是通过对矩阵乘法是多线程实现,让学生加深对线程的理解与调用。
实验步骤:
在Linux操作系统上,利用Linux处理多线程的优点,编写程序用多线程实现矩阵乘法。实现A、B两个矩阵的乘法,并输出计算结果。
实验代码如下:
#include <stdio.h>
#include <time.h>
#include <pthread.h>
#include <stdlib.h>
#include <unistd.h>
#include <memory.h>
#define RANGE 100
#define M 2
#define K 2
#define N 2
void gene_matrix();
void read_matrix();
int matrixA[M][N]={{1,1},{2,2}};
int matrixB[N][M]={{4,14},{5,25}};
int arr[M][M][N];
int res[M][N]={0};
void *func(void *arg);
main()
{
clock_t start=clock();
int i,j,k,cnt,cnt2;
pthread_t tids[N];
…… …… 余下全文
