第一章 函数与极限
第一节 函数
§1.1 函数内容网络图
定义域
不等式
定义
表格法
表达方法 图象法
解析法
非初等函数
函数的特性 奇偶性
函数 周期性
有界性
反函数
重要的函数
复合函数
??1,?符号函数:sgnx??0,
?1,?x?0,x?0, x?0.
几个具体重要的函数 取整函数:f?x??[x],其中[x]表示不超过x的最大整数.
狄里克雷函数:D?x???
?1,?0,x为有理数,x为无理数.
§1.2 内容提要与释疑解难
一、函数的概念
·1·
定义:设A、B是两个非空实数集,如果存在一个对应法则f,使得对A中任何一个实数x,在
B中都有唯一确定的实数y与x对应,则称对应法则f是A上的函数,记为
f:x?y或f:A?B.
y称为x对应的函数值,记为 y?f?x?,x?A.
其中x叫做自变量,y又叫因变量,A称为函数f的定义域,记为D(f),
?
,在平面坐标系Oxy下,集合 f(A)??f(x)x?A?, 称为函数的值域,记为R(f)
?(x,y)y?f(x),x?D?称为函数y=f(x)的图形。函数是微积分中最重要最基本的一个概念,因
为微积分是以函数为研究对象,运用无穷小及无穷大过程分析处理问题的一门数学学科。
1、由确定函数的因素是定义域、对应法则及值域,而值域被定义域和对应法则完全确定,故确
定函数的两要素为定义域和对应法则。从而在判断两个函数是否为同一函数时,只要看这两个函数
的定义域和对应法则是否相同,至于自变量、因变量用什么字母,函数用什么记号都是无关紧要的。
2、函数与函数表达式的区别:函数表达式指的是解析式子,是表示函数的主要形式,而函数除
了用表达式来表示,还可以用表格法、图象法等形式来表示,不要把函数与函数表达式等同起来。
二、反函数
定义 设y=f(x),x?D,若对R(f)中每一个y,都有唯一确定且满足y=f(x)的x?D与之对
应,则按此对应法则就能得到一个定义在R(f)上的函数,称这个函数为f的反函数,记作
f?1:R?f??D或x?f?1?y?,y?R?f?.
?1由于习惯上用x表示自变量,y表示因变量,所以常把上述函数改写成y?f?x?,x?R?f?.
1、由函数、反函数的定义可知,反函数的定义域是原来函数的值域,值域是原来函数的定义域。
2、函数y=f(x)与x=f-1(y)的图象相同,这因为满足y=f(x)点(x,y)的集合与满足x=f-1(y)点(x,y)
的集合完全相同,而函数y=f(x)与y=f-1(x)图象关于直线y=x对称。
3、若y=f(x)的反函数是x=f-1(y),则y?ff??1(y),?x?f?1?f?x??.
4、定理1(反函数存在定理)严格增(减)的函数必有严格增(减)的反函数。
三、复合函数
定义 设y?f?u?,u?E,u???x?,x?D,若D(f)?R?????,则y通过u构成x的函
数,称为由y=f(u)与u???x?复合而成的函数,简称为复合函数,记作y?f(?(x))。 复合函数的定义域为xx?D且?(x)?E,其中x称为自变量,y称为因变量,u称为中间变
量,??x?称为内函数,f(u)称为外函数。
1、在实际判断两个函数y?f(u),u???x?能否构成复合函数,只要看y?f(??x?)的定义域
·2·??
是否为非空集,若不为空集,则能构成复合函数,否则不能复合函数。
2、在求复合函数时,只要指出谁是内函数,谁是外函数,例如y=f(x), y=g(x),若y=f(x)作为外函数,y=g(x)作为内函数。则复合函数y?f(g?x?),若y?g?x?作为外函数,y?f?x?作为内函数,则复合函数为y=g(f(x))。
3、我们要学会分析复合函数的复合结构,既要会把几个函数复合成一个复合函数,又要会把一个复合函数分拆成几个函数的复合。
四 初等函数
常值函数、幂函数、指数函数、对数函数、三角函数、反三角函数统称为基本初等函数。 大家一定要记住基本初等函数的定义域,值域,会画它们的图象,并且要知道这些函数在哪些区间递增,在哪些区间递减,是否经过原点?与坐标轴的交点是什么?以后我们常常要用到。
由基本初等函数经过有限次四则运算或有限次复合运算所得到的函数统称为初等函数。
不是初等函数称为非初等函数。
一般来说,分段函数不是初等函数,但有些分段函数可能是初等函数,例如
2?x,x?0 f?x????x,x?0?x?x,是由y??u,u?x2复合而成。
五 具有某些特性的函数
1.奇(偶)函数
定义 设D是关于原点对称的数集,y=f(x)为定义在D上 的函数,若对每一个
都有f??x???f?x?x?D?这时也有?x?D?,?f??x??f?x??,则称y=f(x)为D上的奇(偶)
函数。
(1)定义域关于原点对称是函数为奇(偶)函数的必要条件。
(2)若f(x)为奇函数,则f(0)=0,事实上,由定义知f(-0)=-f(0),有f(0)=-f(0),得f(0)=0.
2.周期函数
定义 设y=f(x)为定义在D上的函数,若存在某个非零常数T,使得对一切x?D,都有 f(x+T)=f(x),则称y=f(x)为周期函数,T称为y=f(x)的一个周期。
显然,若T是f(x)的周期,则kT?k?Z?也是f(x)的周期,若周期函数f(x)的所有正周期中存在最小正周期,则称这个最小正周期为f(x)的基本周期,一般地,函数的周期是指的是基本周期。 必须指出的是不是所有的周期函数都有最小正周期,例如f(x)=c(c为常数),因为对任意的实常数T,都有f(x+T)=f(x)=c。所以f(x)=c是周期函数,但在实数里没有最小正常数,所以,周期函数f(x)=c没有最小正周期。
如果f(x)为周期函数,且周期为T,任给x?D,有f(x)=f(x+kT),知x?kT?D?k?Z?。所以D是无穷区间,即无穷区间是周期函数的必要条件。
3.单调函数
定义 设y=f(x)为定义在D上的函数,若对D中任意两个数x1,x2且x1<x2,总有
f?x1??f?x2?
?f?x??f?x??, 12·3·
则称y=f(x)为D上的递增(递减)函数,特别地,若总成立严格不等式
f?x1??f?x2??f?x??f?x??, 12
则称y=f(x)为D上严格递增(递减)函数。
递增和递减函数统称为单调函数,严格递增和严格递减函数统称为严格单调函数。
4.分段函数
如果一个函数在其定义域内,对应于不同的x范围有着不同的表达形式,则称该函数为分段函数。
注意分段函数不是由几个函数组成的,而是一个函数,我们经常构造分段函数来举反例,常见的分段函数有符号函数、狄里克雷函数、取整函数。
5.有界函数与无界函数
定义 设y=f(x)为定义在D上的函数,若存在常数N≤M,使对每一个x?D,都有 N?f?x??M
则称f(x)为D上的有界函数,此时,称N为f(x)在D上的一个下界,称M为f(x)在D上的一个上界。
由定义可知上、下界有无数个,我们也可写成如下的等价定义,使用更加方便。
定义 设y=f(x)为定义在D上的函数,若存在常数M>0,使得对每一个x?D,都有
f?x?M
则f(x)为D上的有界函数。
几何意义,若f(x)为D上的有界函数,则f(x)的图象完全落在直线y=-M与y=M之间。
注意:直线y=-M,y=M不一定与曲线相切。有界函数定义的反面是
定义 设y=f(x)为定义在D上的函数,若对每一个正常数M(无论M多么大),都存在x0?D,使f?x0?M,则称f(x)为D上的无界函数。
6.函数的延拓与分解
有时我们需要由已知函数产生新的函数来解决实际问题,这里我们从函数的特性出发,开拓由已知产生新的函数的方法。
设y?f?x?,x??0,a?,我考虑区间[-a,a]上的函数F(x),它是偶函数,且在[0,a]上,使F(x)=f(x),则应有F?x????f?x?,
?f??x?x??0,a?, x???a,0?.
称F(x)是f(x)的偶延拓
同样可给出f(x)的奇延拓,即函数F(x)在[-a,a]上的奇函数,且在(0,a)上,F(x)=f(x),
?f?x?,x??0,a??x?0则应有F?x???0,这样,研究f(x)只要,研究F(x)就可以了。
??f??x?,x???a,0??
·4·
同样,对于函数y=f(x),x??a,b?,可以构造一个以(b-a)为周期的周期函数F(x),在(a,b)上,F(x)=f(x),则有F?x????f?x?,x??a,b? ?f?x?n?b?a??,x??nb??n?1?a,?n?1?b?na?,n?z
这就是函数f(x)的周期延招,研究f(x)只要研究F(x)就可以了。
此外,定义在区间(-a,a)上的任何一个函数f(x)都可以表示成一个奇函数与一个偶函数和事实
f?x??f??x?f?x??f??x?? 22
f?x??f??x?f?x??f??x?,f2?x??, 设f1?x??22上f?x??
由奇偶函数的定义知,f1(x)是奇函数。 f2(x)是偶函数,且f?x??f1?x??f2?x?.
我们还可以证明f1(x),f2(x)是唯一存在,如果f?x??g1?x??g2?x?,
其中g1(x)是奇函数,g2(x)是偶函数,于是
f?x??g1?x??g2?x?,f??x??g1??x??g2??x???g1?x??g2?x?,
解得g1?x??
f?x??f??x?f?x??f??x??f1?x?,g2?x???f2?x? 22
§1.3解题基本方法与技巧
一、求函数定义域的方法
1.若函数是一个抽象的数学表达式子,则其定义域应是使这式子有意义的一切实数组成的集合,且在
(1)分式的分母不能为零; (2)偶次根号下应大于或等于零;
(3)对数式的真数应大于零且 底数大于零不为1; (4)arc sin
(5)tan??x?,其k??其?x??1; ??x?或arccos??x?,?
2???x??k???
2,k?z;cot??x?,其k????x??k???,k?z.
(6)若函数的表达式由几项组成,则它的定义域是各项定义域的交集;
(7)分段函数的定义域是各段定义域的并集。
2.若函数涉及到实际问题,定义域是除了使数学式子有意义还应当确保实际有意义自变量取值全体组成的集合。
3.对于抽象函数的定义域问题,要依据函数定义及题设条件。
例1 求下列函数的定义域:
(1)y?3x?x3; (2)y?arcsin2x 1?x
3 解(1)要使函数式子有意义,就必须满足3x?x?0。
化简有 xx?3x?3?0, ????
·5·
????
解之,得定义域为x????,????0,?。 即 x?xx?3?0. (2)要使函数式子有意义,就必须满足
2x2x?1, ?1,即?1?1?x1?x
22?1,?3????1, 1?x1?x
311?, 不等式各边除以(-2)有,?21?x2
21各边取倒数得,?1?x?2。解之,得函数的定义域为??x?1。 33化简有?1?2?
例2 不清设f?x??x
11?x?2,求f(x)的定义域。
解 要使函数式子有意义,必须满足
1??1??0 即 ?x?2??x?2?0?x?1 ?x?2?
故所给函数的定义域为?x:x?R且x?1,x?2?。 注意:如果把x
1?1
x?2化简为x?x?2?,那么函数的定义域为x?1的一切实数,因此,求函x?1
数的定义变形式时需特别小心,避免出错。
例3 已知f?x??ex,f???x???1?x且??x??0,求??x?并写出它的定义域。 2
解 由e???x??2?1?x,得??x??ln1?x,
由ln?1?x??0,得1?x?1,即x≤0,所以 ??x??ln1?x,x?0。 例4 设f(x)的定义域为[0,1],试求f(x+a)+f(x-a)的定义域(a>0)。
解 要使f(x+a)+f(x-a)有意义,必须满足
0?x?a?1,?a?x?1?a, ? 得 ? ???0?x?a?1,?a?x?1?a.
当0?a?11时,由a?1?a,知函数的定义域为a?x?1?a。当a?时,由a>1—a,知定义22
域不存在。
·6·
二、求函数值域的方法
1. 由定义域x的范围,利用不等式求出f(x)的范围;
2. 若y=f(x)有反函数x=f--1(y),求出反函数的定义域就是函数的值域;
3. 利用一元二次方程的判别式求函数的值域。
例5 求下列函数值域:
x?1x2?2x?1(1)y?x??x; (2)y?; (3)y?2。 x?3x?x?1
?1?55 解(1)令?x?t,则x?1?t2,于是y?x??x?1?t2?t???t????。 ?2?44
当且仅当t?23515??,即x?时,y?。故函数y?x??x的值域是???,?。 4424??
(2)由y?x?1x?11?3y,得(x+3)y=x+1,解之,x?是y?的反函数,而 x?3x?3y?1
x?1?3y的定义域是y?1,故函数值域是???,1???1,???。 y?1
(3)由原函数式变形,得 y?x?x?1??x?2x?1,即 22
?y?1?x2??y?2?x?y?1?0。
当y-1=0,即y=1时,x=0;当y?1?0,即y?1时,
???y?2??4?y?1??0,即0?y?4?y?1?。故函数的值域为[0,4]。 22
三、判断两函数是否为同一函数的方法
例6 判断下列各组函数是否为同一函数:
(1)(i)y?sinx?0?x???; (ii)s??cos2t?0?t???,
(2)(i)y?x?11y?; (ii)。 x2?1x?1
解(1)由y=sinx的定义域是[0,π],s??cos2t的定义域是[0,π]。知两函数定义域相同,又S??cost?
为同一函数。
(2)由y?2sin2t?sint?sint?0?t???,知两函数对应法则相同,故(i)(ii)x?11x??1y?的定义域是的全体实数,的定义域是x??1的全体实数,2x?1x?1
·7·
知两函数定义域不同,尽管当x??1时,y?
不是同一个函数。
x?11?,知两函数对应法则相同,但(i)(ii)x2?1x?1
四、求反函数方法
步骤:1. 从y=f(x)中解出x=f--1(y) ;2.改写成y=f--1(x),则y=f-1(x)是x=f-1(y)的反函数. 例7 求下列函数的反函数: ——
(1)y??x2??1?x?0?; (2)y?3x??x2?3x??x2;
??x,2x?1, (3)y??x,1?x?4,
x??2,x?4.
2 解(1)由x???y,y??0,1?,知反函数为y???x2, x??0,1?。
22 (2)由y?x??x?x??x
两边立方得 y?x??x?3x??x
3322x?2?x22?3(x??x)x??x222?x?2?x2,即 y?2x?3x??x?3x??x
解之 x?
所以反函数为y??2x?3y, 1?3y?y3?。 213x?x3,x?R. 2??
?y,y?1,?x,x?1,??(3)由 x??y,1?y?16, 则反函数为 y??x,1?x?16,
???log2x,x?16.?2y,y?16,
五、求复合函数的方法。
1.代入法
某一个函数中的自变量用另一个函数的表达式来替代,这种构成复合函数的方法,称之为代入法,该法适用于初等函数的复合,关健搞清谁是内函数,谁是外函数。
2.分析法
根据外函数定义的各区间段,结合中间变量的表达式及中间变量的定义域进行分析,从而得出复合函数的方法,该方法用于初等函数与分段函数或分段函数与分段函数的复合。
例8 设f?x??,求fn?x??f?f?f?x???.. ????????xn次2x
·8·
x
x
解 fx22?x??f?f?x???
f?x???f
2
x?
?f
2
x?
?x22
?
x?x?2x
2
,
1?x2
x
x?
2
f3?x??f?f?f?x????f?f2?x???f2??f2
??2x
?x2x?
x2?3x2, 1?2x2
猜想 fn?x??
x?nx
2
。
当n=1时,结论已成立,假设n=k时,fk?x??
x?kx
2
成立,当n=k+1时,
x
f?kx2
k?1?x??f?fk?x????x。1?
x2?k?1x2
1?kx2
即n=k+1时结论成立,故fn?x??
x?nx
2
。
例9 设f?x?????
1,x?1,
?f?f?x??。
?0,x?1,
求 解 当x?1时,f?x??1,f?f?x???f?1??1,
当x?1时,f?x??0,f?f?x???f?0??1。
故 f(f(x))=1。
例10 设f?x????
ex
,x?1.
,?x,x?1??x????x?
x2
??21,,xx??00,,求f???x??。
由f???x?????
e??x? 解,
??x??1,
???x?,
??x??1.
(1)当??x??1时 或x?0,??x??x?2?1,
即??x?0,?
x??1,有x??1。 9··
或x?0,??x??x?1?1,2?x?0,即?,有0?x?2. ?2?x?2?
(2)当??x??1时
或x?0,??x??x?2?1,
或x?0,x?0,即??x??1,有?1?x?0。 ???x??x?1?1,2?x?0,即?,有x?2.得 x??2或x?2?
x?2?e,x??1,?x?2,?1?x?0, f???x????x2?1 e,0?x?2,?2?x?1,x?2
六、判断奇偶函数的方法
偶函数f(x)的图象关于y轴对称;奇函数f(x)的图象关于原点对称。
奇偶函数的运算性质
1. 奇函数的代数和仍为奇函数,偶函数的代数和仍为偶函数。
2. 偶数个奇(偶)函数之积为偶函数;奇数个奇函数的积为奇函数。
3. 一奇一偶的乘积为奇函数
4. 两个奇函数复合仍为奇函数,一奇一偶复合为偶函数,两个偶函数复合仍为偶函数。
判断方法
1.用定义
2..若f(x)+f(-x)=0,则f(x)为奇函数,这种方法适合用定义比较困难的题目。
例11 判断下列函数的奇偶性:
(1)f?x??1?x?1?x; (2)f?x??ln221?x; 1?x
(3)f?x??11?(a>0,a≠1常数) xa?12
2222 解(1)由f??x??1??x?1?x?1?x?1?x?f?x?,知f(x)为偶函数
(2)由f?x??f??x??ln
?ln1?x1???x??ln 1?x1??x1?x1?x1?x1?x?ln?ln??ln1?0,知f(x)为奇函数。 1?x1?x1?x1?x
(3)由f??x??1
a?x111ax1a1???????1? xx121?a?1221?a2?1ax·10 ·
ax?1?ax11111????????f?x?,知f(x)为奇函数 ?xxx1?a21?a2a?12
七、周期函数的判断与周期的求法
1.周期函数周期的求法
(1)若T为f(x) 的周期,则f(ax+b)的周期为T?a?0? a
(2)若f(x)的周期为T1,g(x)的周期为T2,则c1f(x)+c2g(x)的周期为T1,T2的最小公倍数。
2.周期函数的判断方法。
(1)用定义。
(2)用周期函数的运算性质。
常见函数的周期:sinx,cosx,其周期T=2π;tanx,cotx,sinx,cosx,其周期T=π。
例12 求下列函数周期
(1)f?x??2tanxx?3tan; (2)f?x??sin4x?cos4x; (3)f?x??x??x?。 23
解(1)由tan?xx?的周期T1? ?2?,tan的周期T2??3?。故f(x)的周期性期为6π。1123
32
2 (2)由f??x???sin2x?cos2x??2sin2xcos2x
?1?121312?1sin2x?1??1?cos4x???cos4x,知f(x)的周期T???。 244442
(3)设x?n?r?0?r?1?,n?Z,T为任意整数,由
f?x?T??f?n?T?r??n?T?r??n?T?r??n?T?r??T??n?r???n?r??n?r??f?x?知任意整数均为其周期,则最小周期T=1。
例13 若函数f?x?????x????的图形关于两条直线x=a和x=b对称(b>a),则f(x)为周期函数。
证 由条件函数的对称性知
f?a?x??f?a?x?, (1)
f?b?x??f?b?x?, (2)
故函数在a,b中点(a+b)/2处的值等于点a?b?ab?a/和b?处的函数值 22
从而猜想如果f(x)为周期函数,则周期应为 ?b?
??b?a??b?a??a?????2?b?a?。 2??2?·11·
事实上f?x?2?b?a???f?b??x?b?2a???f?b??x?b?2a???f?2a?x?
?f?a??a?x???f?a??a?x???f?x?
所以f(x)是以2(b-a)为周期的周期函数。
八、单调函数的判断方法
1.用定义。
2.利用单调函数的性质。
(1)两个递减(增)函数的复合是递增函数,一个递增、一个递减函数的复合是递减函数。 例14 设??x?,??x?及f(x)为递增函数证明:若
则 ??x??f?x????x? (1) ????x???f?f?x???????x?? (2)
证 设x0为三个函数公共域内的任一点,则 ??x0??f?x0????x0?
由(1)以及函数f(x)的递增性知f???x0???f?f?x0??,????x0???f???x0??;
从而 ????x0???f?f?x?? 0
同理可证 f?f?x0???????x0??。
由x0的任意性知,于是(2)式成立。
九、函数有界性的判断
判断函数是否有界,经常用定义。
例15 判断下列函数是否有界:
(1)f?x??x1??fx?,x??0,1?。 ; (2)221?xx
解(1)由f(x)的定义域是R。
当x?0时,f?x??
知x?R时,f?x??xxx11???????x?0时,f0?0,有f0?,当, 1?x21?x22x221,所以f(x)为有界函数。 2
(2)?M?0,取x0?1
M?1??0,1?。 f?x0?? 1?M?1?M?1?M.M?1
由无界函数的定义知f(x)在(0,1)上无界。
·12 ·
第二节 函数极限与连续
§2.1 函数极限内容网络图
?limf(x)?A?x??
limf(x)?A?x??x0 函数极限定义 ?limf(x)???x?x0?limf(x)????x??
性质??唯一性,有界性,不等式 ,保号性,四则运算 夹逼定理
单调有界定理
单侧极限与双侧极限
函数极限与数列极限——归结原则。
函数极限与连续关系定理 函数极限与无穷小
无穷大与无穷小
无穷小的阶——高阶、同阶、等价。
函数连续定义——limf(x)?f(x0)或lim?y?0 x?x0?x?0
可去间断点
跳跃间断点
间断点分类
最大(小)值定理 闭区间上连续函数的性质
初等函数在其定义域内的零值点定理(根的存在定理) 闭区间上连续 介值定理
§2.2内容提要与释疑解难
一、函数极限的概念
1.limf(x)?A:若存在一个常数A,???0,?X?0,当x?X时,都有f(x)?A??。 x???
2. limf(x)?A:把1中“x?X”换成“x??X”。 x???
·13·
3. limf(x)?A:把1中“x?X”换成“x?X”。 x??
定理limf(x)?A?limf(x)?A且limf(x)?A. x??x???x???
4.limf(x)?A:设f(x)在x0的某空心邻域内U?x0?有定义,若存在一个常数A,x?x00
???0,???0,当0?x?x0??时,都有f(x)?A??。
f(x)?A: 设f(x)在x0的某左半邻域U?(x0)内有定义,若存在一个常数A,5.lim?x?x00
???0,???0,当???x?x0?0时,都有f(x)?A??。
?此时也可用记号f(x0?0)或f(x0)表示左极限值A,因此可写成
x?x0limf(x)?f(x0?0)或lim?f(x)?f(x0) ?x?x0?
f(x)?A:设f(x)在x0的某右半邻域U?(x0)内有定义,若存在一个常数6. lim?x?x00
?A,???0,???0,当0?x?x0?8?时,都有f(x)?A??。此时也可用f(x0?0)或f(x0)表
示右极限A。因此可写成limf?x??f?x0?0?或limf(x)?fx0。 ???x?x0x?x0??
f?x??A且limf?x??A. 定理 limf?x??A?lim??x?x0x?x0x?x0
该定理是求分界点两侧表达式不同的分段函数在该分界点极限是否存在的方法,而如果在x0的左右极限存在且相等,则在该点的极限存在,否则不存在。
7.limf(x)??:?M?0,???0,当0?x?x0??时,都有f(x)?M。此时称x?x0时,x?x0
f(x)是无穷大量。
而limf(x)???,只要把公式中“f(x)?M”改成“f(x)?M”,limf(x)???,只x?x0x?x0
要把上式中“f(x)?M”改成“f(x)??M”。
8.limf(x)??:?M?0,?X?0。当x?X时,都有f(x)?M。 x??
读者同理可给出lim(??或??)f(x)??(??或??)定义。 x??
注:limf(x)?A(常数)与limf(x)??的区别,前者是表明函数极限存在,后者指函数x?x0x?x0
极限不存在,但还是有个趋于无穷大的趋势。因此,给它一个记号,但还是属于极限不存在之列,·14 ·
以后,我们说函数极限存在,指的是函数极限值是个常数。
9.limf(x)?0。称f(x)当x?x0是无穷小量。这里的x0可以是常数,也可以是x?x0
??,??或?。
定理 limf(x)?A(常数)?f(x)?A??(x)。 x?x0
其中lim?(x)?0。 x?x0
10.若???0,?M?0,当x?U(xx,?)时,都有f(x)?M,称f(x)当x?x0时是有界量。 0
二、无穷小量阶的比较,无穷小量与无穷大量关系
设limf(x)?0,limg(x)?0, x?x0x?x0
(这里x0可以是常数,也可以是?,??,??,以后我们不指出都是指的这个意思)
(1)若limx?x0f(x)?0,称f(x)当x?x0时是g(x)的高阶无穷小量,记作 g(x)
f(x)??(g(x))(x?x0).。
(2)若limx?x0f(x)?c(常数)?0,,称f(x)当x?x0时是g(x)的同价无穷小量。 g(x)
f(x)?1,称f(x)当x?x0时是g(x)的等价无穷小量,记作g(x)(3)若limx?x0
f?x?~g?x??x?x0?,此时(2)式也可记作f?x?~cg?x??x?x0?。
(4)若limx?x0f(x)x?x0k?c(常数)?0(k?0常数),称f(x)当x?x0时是x?x0的k阶无穷小
量。
由等价无穷量在求极限过程中起到非常重要的作用,因此,引入 若limx?x0f(x)?1。记作f(x)~g(x)(x?x0), g(x)
如果f(x),g(x)均是无穷小量,称为等价无穷小量;如果f(x),g(x)均是无穷大量,称为等价无穷大量;如果f(x),g(x)既不是无穷小也不是无穷大,我们称为等价量。
·15·
例如 limf(x)?A(常数)?0,则f(x)~A(x?x0)。 x?x0
注:A不能为零,若A=0,f(x)不可能和0等价。 无穷小量的性质:
1.若?1(x),?2(x),?,?m(x)当x?x0时,均为无穷小量,则 (i)lim?c1?1(x)?c2?2(x)???cm?m(x)??0. x?x0
其中c1,c2,?cm均为常数。
(ii)lim?1(x)?2(x)??m(x)?0。 x?x0
2.若f(x)当x?x0时是有界量,?(x)当x?x0时是无穷小量,则limf(x)?(x)?0。 x?x0无穷大量的性质:
1.有限个无穷大量之积仍是无穷大量。
2.有界量与无穷大量之和仍是无穷大量。 无穷小量与无穷大量之间的关系: 若limf(x)??,则limx?x0x?x01?0; f(x)
若limf(x)?0,且???0,当x?U(x0,?)时f(x)?0,则limx?x0x?x01??。 f(x)
三、函数连续的概念。
定义1 若limf(x)?f(x0),称f(x)在x?x0处连续。 x?x0
用???语言可写为
定义 设f(x)在x0的某邻域U(x0)内有定义,若???0,???0,x?x0??时,都有f(x)?f(x0)??,称f(x)在x?x0处连续。 用函数值增量?y形式可写为
?y?0,称f(x)在x?x0处连续。 定义 若lim?x?0
f(x)?f(x0),称f(x)在x?x0处左连续。 若lim?x?x0
f(x)?f(x0),称f(x)在x?x0处右连续。 若lim?x?x0
·16 ·
定理f(x)在x0处连续?f(x)在x0处既是左连续又是右连续。
如果f(x)在x?x0处不连续,称x?x0为f(x)的间断点。
间断点的分类:
(1)若limf(x)?A(常数),但f(x)在x?x0处不连续,称x?x0是f(x)的可去间断点。 x?x0
若x?x0为函数f(x)的可去间断点,只须补充定义或改变f(x)在x?x0处的函数值,使函数在该点连续。但须注意,这时函数与f(x)已经不是同一个函数但仅在x?x0处不同,在其它点相同。我们正是利用这一性质去构造一个新的函数F(x),使F(x)在某闭区间上处处连续,因而有某种性质。当x?x0时,也具有这种性质。而x?x0时,F(x)?f(x),所以f(x)在x?x0的范围内也具有这种性质,从而达到了我们的目的。
例如 f(x)?sinxsinx,limf(x)?lim?1, x?0x?0xx
?sinx?,x?0,但f(x)在x?0处没定义 ,知f(x)在x?0处不连续,设F(x)??x??1,x?0.
则F?x?在x?0处连续,但F?x?与f?x?定义域不同,
?sinx?,x?0,虽然F(x)与f(x)不是同一函数 ,但在x?0处完全相同,又如f(x)??x?x?0.?0,
?sinxsinx?,x?0,limf(x)?lim?1?f(0)?0,知f(x)在x?0处不连续。设F(x)??x x?0x?0x?x?0.?1,
则F(x)在x?0处连续,虽然F(x)与f(x)定义域相同,但在x?0处,两个函数值不同,知F(x)与f(x)不是同一函数,但仅在x?0不同,其余点函数值处处相同。
f(x)?f(x0?0).limf(x)?f(x0?0),但f(x0?0)?f(x0?0),称x?x0为(2)若lim??x?x0x?x0
f(x)的跳跃间断点,称f(x0?0)?f(x0?0)为f(x)的跳跃度。
(1)(2)两种类型的特点是左右极限都存在,我们统称为第一类间断点。
(3)若x0处,左、右极限至少有一个不存在,我们称x?x0为f(x)的第二类间断点。 ·17·
若limf(x)??,我们也称x?x0为f(x)的无穷型间断点,属于第二类间断点。 x?x0
四、函数极限的性质
在下述六种类型的函数极限:
(1)limf(x) (2) limf(x) (3) limf(x) (4) limf(x) x???x???x??x?x0
f(x) (6)limf(x) (4) lim??x?x0x?x0
它们具有与数列极限相类似的一些性质,我们以limf(x)为例,其它类型极限的相应性质的叙述只x?x0
要作适当修改就可以了。
性质1(唯一性)若极限limf(x)存在,则它只有一个极限。 x?x0
性质2(局部有界性)若极限limf(x)存在,则存在x0的某空心邻域U(x0),使f(x)在U(x0)x?x000
内有界。
注意:limf(x)存在,只能得出f(x)在x0的某邻域内有界,得不出f(x)在其定义域内有界。 x?x0
性质3 若limf(x)?A,limg(x)?B,且A?B,则存在x0的某空心邻域U(x0,?0),使x?x0x?x00
x?U(x0,?0)时,都有f(x)?g(x)。
性质4(局部保号性) 若limf(x)?A?0(或?0),则对任何常数0???A(或A???0),x?x00
存在x0的某空心邻域U(x0),使得对一切x?U(x0),都有 f(x)???0(或f(x)???0)成立。
性质5(不等式)若limf(x)?A,limg(x)?B,且存在x0的某空心邻域U(x0,?0),使x?x0x?x0000
得对一切x?U(x0,?0),都有f(x)?g(x),则A?B。
性质6 (复合函数的极限)若lim?(x)?u0,limf(u)?A,且存在x0的某空心邻域x?x0u?u00
U(x0,??),当x?U(x0,??)时,?(x)?u0 ,则limf[?(x)]?limf(u)?A。 x?x0u?u000
性质6是求极限的一个重要方法——变量替换法,即
x?x0limf(?(x))令?(x)?ulimf(u)?A。 且x?x0,?(x)?u0u?u0
性质7(函数极限的四则运算)若limf(x)与limg(x)x?x0x?x0均存在,则函数
f(x)?g(x),f(x)?g(x),cf(x)(c为常数)在x?x0时极限均存在且
·18 ·
(1)lim?f(x)?g(x)??limf(x)?limg(x); (2)lim?f(x)?g(x)??limf(x)?limg(x); x?x0x?x0x?x0x?x0x?x0x?x0
(3)limcf(x)?Climf(x);又若limg(x)?0,则x?x0x?x0x?x0f?x?在x?x0时的极限也存在,且有 gxlimf(x)f(x)x?x0(4)lim。 ?x?x0g(x)limg(x)
x?x0
利用极限的四则运算,可得下列重要结果。
a0xn?a1xn?1??an?1x?anlim(a0,?,an,b0,?,bm均为常数,a0?0,b0?0) x??bxm?bxm?1???b01m?1x?bm
11?L?a?ann?1n?1xn?limmx??x11b0?b1?L?bm?1m?1?bmxxa0?a1
上面的结论可作为公式用。
性质8(归结原则或海涅(Heine)定理)limf(x)存在的充要条件是: x?x0?0,n?m1?a0n???,n?m 1?b0xm???,n?m
?limxn?x0?xn?x0,n?1,2,??,极限limf(xn)都存在且相等。 n??n??
逆否定理若存在两个数列??????,?xn,xn
n??limn???=x0,limxn??=x0,且xnn??n???)?A,limf(xn??)?B,A?B或存在?xn?,limxn?x0,limf(xn)不存在,则limf(x0)不limf(xnn??n??n?x0
存在。
此定理是判断函数极限不存在的一个重要方法。
五、函数连续的性质
若函数f(x)在点x?x0处连续,即limf(x)?f(x0),利用极限的性质1-5可得到函数在x?x0
x?x0连续的局部有界性,局部保号性,不等式等,只要把U(x0)改成U(x0)即可,读者自己叙述出来。
利用极限的四则运算,我们有
性质1(连续函数的四则运算)若f(x),g(x)在点x?x0处连续,则0f(x)?g(x),f(x)g(x),cf(x)(c为常数)f(x)(g(x0)?0)在x?x0处也连续。 g(x)
性质2 若u??(x)在x0处连续,y?f(u)在u0??(x0)处连续,则y?f(?(x))在x?x0处 ·19·
也连续且limf(?(x))?f(?(x0))?f(lim?(x)) x?x0x?x0
在满足性质2的条件下,极限符号与外函数f可交换顺序,如果仅要可交换顺序,有
,则推论 若lim?(x)?u0,y?f(u)在u?u0处连续x?x0x?x0limf(?(x))?f(lim?(x))。 x?x0
证 设g(x)????(x),x?x0,则g(x)在x?x0处连续,又y?f(u)在u?uo?g(x0) ?u0,x?x0,
x?xox?xo处连续,由性质2知limf(g(x))?f(limg(x))。
由于x?x0,要求x?x0,有g(x)??(x),所以limf(?(x))?f(lim?(x))。 x?xox?xo
在这里,我们巧妙地利用可去间断点的性质,构造一个连续函数,以满足所需的条件,上面的性质2及推论也是求函数极限的一个重要方法。
即极限符号与外函数f交换顺序,把复杂函数极限转化为简单函数极限。
定理 初等函数在其定义域上连续。
六、闭区间上连续函数的性质
定理 (最大值与最小值定理)若f(x)在闭区间?a,b?上连续,则f(x)在?a,b?上一定能取到最大值与最小值,即存在x1,x2??a,b?,f(x1)?M,f(x2)?m,使得对一切x??a,b?,都有m?f(x)?M。
推论1 若f(x)在闭区间?a,b?上连续,则f(x)在?a,b?上有界。
定理(根的存在定理或零值点定理)若函数f(x)在闭区间?a,b?上连续,f(a)f(b)?0,则至少存在一点??(a,b),使f(?)?0。
推论1 若函数f(x)在闭区间?a,b?上连续,且f(a)?f(b),c为介于f(a),f(b)之间的任何常数,则至少存在一点??(a,b),使f(?)?c。
?a,b?上连续,则值域R(f)??m,M?。 推论2 若函数f(x)在闭区间
这几个定理非常重要,请大家要记住这些定理的条件与结论,并会运用这些定理去解决问题。
七、重要的函数极限与重要的等价量
利用初等函数的连续性及极限符号与外函数的可交换性及等价量替换,夹逼定理可得到下面的·20 ·
重要的函数极限。
sinx?1. 2. lim(1?x)x?e. 1.limx?0x?0x1
ln(1?x)13.lim?limln(1?x)?limln(1?x)x?lnlim(1?x)x?lne?1. x?0x?0xx?0x?0x
ex?1t1设ex?1?tlim?lim?1. 4.limx?0t?0ln(x1?t)t?0ln(1?t)
t11
ax?1exlna?1?lim?lna?lna(a?0,a?1为常数). 5. limx?0x?0xxlna
(1?x)b?1ebln(1?x)?1ln(1?x)6、lim?lim??b?b(b为常数,b?0). x?0x?0xbln(1?x)x
7.limx?0arcsinxt1设arcsinx?tlim?lim?1. t?0sintt?0sintx
t
arctanxtt设arctanx?tlim?lim?cost?1?1?1. x?0t?0t?0xtantsint
lnx?0(k?0常数). 9. limx???xk8.lim
xk
10. limx?0(a?1常数,k为常数). x???a
11.若limu(x)?a?0,limv(x)?b(a,b均为常数),则 x?x0x?x0
x?x0limu(x)V(x)?limex?x0
v(x)V(x)lnu(x)?ex?x0limV(x)lnu(x)=ex?x0limV(x)?limlnu(x)x?x0?eblna?elna?ab b即 limu(x)x?x0?ab。
注:不仅要记住这些公式的标准形式,更要明白一般形式。即上面公式中的x可换成f(x),只要x?xo时,f(x)?0,结论依然成立。
利用上述重要极限,我们可以得到下列对应的重要的等价无穷小量,在解题中经常要利用他们 当x?0时,sinx~x,ln(1?x)~x,e?1~x,a?1~xlna(a?0,a?1,常数). xx
·21·
(1?x)b?1~bx(b?0,常数),arcsinx~x,arctanx~x,1?cosx~12x. 2
注:上式中的x可换成f(x),只要x?x0时,f(x)?0.结论依然成立。
例如 sinf(x)~f(x)(若x?x0时,f(x)?0)。
此外,若limf(x)?A(常数)?0,f(x)~A(x?x0). x?x0
§2.3 解题基本方法与技巧
一、求函数极限的有关定理
等价量替换定理,若
(1)f(x)~f1(x),g(x)~g1(x),h(x)~h1?x?(x?x0);
(2)limx?x0f1(x)g1(x)f(x)g1(x)f(x)g(x),则lim?A(或?);?lim1?A(或?). x?xx?x00h1(x)h(x)h1(x)
证limx?x0f(x)g1(x)f(x)g(x)h1(x)f(x)g(x)?lim1???A?1?1?1?A(或?), x?x0h(x)h1(x)f1(x)g1(x)h(x)
即limx?x0f(x)g1(x)f(x)g(x)?lim1?A(或?). x?x0h(x)h1(x)
这个定理告诉我们,在求函数极限时,分子、分母中的因式可用它的简单的等价的量来替换,以便化简,容易计算。但替换以后函数极限要存在或为无穷大。需要注意的是,分子、分母中加减的项不能替换,应分解因式,用因式替换,包括用等价无穷小量、等价无穷大量或一般的等价量来替换。
夹逼定理 若 limf(x)?limg(x)?A,且存在x0的某空心邻域U(x0,??),使得对一切x?x0x?x00
x?U(x0,??),都有f(x)?h(x)?g(x),则 limh(x)?A。 x?x00
f(x)存在。单调有界定理(1)若f(x)在U?(x0)内递增(或递减)有下界(或上界),则lim ?x?x00
(2)若f(x)在(??,a)内递增(或递减)有下界(或上界),则limf(x)存在。 x???
请读者给出x?x0,x???的叙述。函数的单调有界定理应用的较少,大家只要了解就可以。 ?
)法则I 设 洛必达(L?Hospital
(1)limf(x)?0,limg(x)?0; x?x0x?x0
·22 ·
(2)存在x0的某邻域U(x0),当x?U(x0)时,f?(x),g?(x)都存在,且 g?(x)?0;
(3)limx?x000f?(x)f(x)f?(x)?A(或?),则lim?lim?A(或?). x?x0g(x)x?x0g?(x)g?(x)
洛必达(L?Hospital)法则II,设
(1)limf(x)??,limg(x)??; x?x0x?x0
(2)存在x0的某邻域U(x0),当x?U(x0)时,f?(x),g?(x)都存在且 g?(x)?0;
(3)limx?x000f?(x)f(x)f?(x)?A(或?),则lim?lim?A(或?). x?xx?x0g(x)0g?(x)g?(x)
??1.上述两个法则中的x?x0改成x?x0,x?x0,x??,x???,x???时,条件(2)
只须作相应的修改,结论依然成立。
2.在用洛必达法则求极限之前,应尽可能把函数化简,或把较复杂的因式用简单等价的因式来替换,以达到简化,再利用洛必达法则。
3.利用洛必达法则求极限时,可在计算的过程中论证是否满足洛必达法则的条件,若满足洛必达法则的条件,结果即可求出;若不满足,说明不能使用洛必达法则,则需用其它求极限的方法。此外,可重复使用洛必达法则,但只能用有限次。
注:洛比达法则是第三章内容。
二、函数极限的类型
1. 若f(x)是初等函数,x0?f(x)的定义域,由初等函数的连续性知limf(x)?f(x0). x?x0
2.若limf(x)?A,limg(x)?B,则 x?x0x?x0
?AA常数,B常数?0,?B,
?0,A?0,B??,?f(x)??,A??,B?0,??(1)lim 0x?x0g(x)?"",A?0,B?0,0???A??,B??.?"",??
?AB,?(2)limf(x)g(x)???,x?x0?"0?",?
A常数,B常数,A?常数?0,B??, A?0,B??.·23·
A?0,B??时,limf(x)?g(x)(0,?)lim
x?x0
x?x0
f(x)0g(x)?
()或lim()??,???.
x?x0101?
g(x)f(x)
对于因式中含有对数函数,反三角函数时,一般放在分子、否则利用洛必达法则很繁,或求不出来。
?A?B,
????
(3)lim(f(x)?g(x))??
x?x0
?????"???"
x?x0
A常数,B常数,
A、B中有一个是常数,另一个是无穷大,A、B为异号无穷大,A、B为同号无穷大,
当A??,B??,且A、B同号时,lim??f?x??g?x??.
这时,把f?x?,g?x?化成分式,通分、化简,化成“
0?
”或“”,再利用洛必达法则。 0?
lim
(4)x?x0
f?x?
g?x?
?AB,???"1",?"00",???0
"??",??0,???,?
A常数?0,B常数,A?1,B??A?0,B?0A??,B?0,A?0,B???A?0,B???
(i)当A?1,B??时,
lim
我们有两种方法求该未定式的极限,一种方法利用重要极限x?0
?1?x?
1x
来计算,另一种方法,
化为以e为底的指数函数,再利用洛必达法则。即
解法一
limx?x0
f?x?
g?x?
?1??
?
limx?x0
?fx?1?????1??f?x??1???????
1
?f?x??1?g?x?
?ex?x0
lim?f?x??1?g?x??0.??
.
再根据具体情况化成""或"
0?"。 ?
解法二
limx?x0
f?x?
g?x?
?1??
?
limx?x0
elnf?x?
g?x?
g?x?lnf?x?
?lim?ex?x0e
x?x0
lim
lnf?x??0?
???0?gx.
这两种方法,我们经常还是利用解法一方便。
(ii)当A?0,B?0时,(iii)当A??,B?0时
这时,只有化成以e为底的指数函数,再利用洛必达法则。即
·24 ·
x?x0limf(x)g(x)(00)(?0)?limeg(x)lnf(x)?ex?x0x?x0limg(x)lnf(x)(0??)(0??)?elnf(x)??()()1x?x0??g(x)lim.
而A?0,B???或A?0,B???时不属于未定式,因为
x?x0limf(x)
limf(x)g(x)(0)?limex?x0??g(x)lnf(x)?e?ex?x0limg(x)lnf(x)????(??)??e???0。 ?e?????。 g(x)
x?x0(0)?limex?x0??g(x)lnf(x)x?x0limg(x)lnf(x)????(??)?
三、已知函数的表达式,求函数的极限
1.求函数极限的四种重要方法
(1)极限的四则运算;(2)等价量替换;(3)变量替换;(4)洛必达法则。
对于未定式的极限,先用等价量替换或变量替换或极限的四则运算化简,再利用洛必达法则求极限。很多情况下,这几种方法常常综合运用。
例1 求limx?0x?arcsinx. 3x
解 lix?0x?arcsixn0()=lim3x?00x1??12(1?x)2(?2x)21?x0()?lim??。 2x?006x63x13
例2 求lim?x?01?cosxx(1?cosx).
解 lim?x?001?cosx()?lim, x?0?x(1?cosx(1?cosx)0x)(1?osx)1?x
1由x?0时,1?cosx~2,1?cosx~2x?2xx2
?,1?cosx~,得 22
x2
?1。 原式=limx?0?x2x??22
注:本题虽然是未定式,但巧妙地用变量替换,并没用洛必法则就直接求出了极限。
例3 求limx?0?tanx??sinx。 2xln(1?x)?x
tanx?sinx
xln1(?x)?x?tanx??sinx解 原式?limx?0
·25·
?limx?0sinx(1?cosx), xln(1?x)?x?tanx??sinxcosxx2
,由x?0时,sinx~x,1?cosx~2?tanx??sinx~2,cosx~1,得
x2
x?1x20?lim() 原式?limx?02xln(1?x)?x4x?0ln(1?x)?x0
?12x1x(1?x)1lim?lim??。 4x?012x?0?x2?11?x?x2?cosx例4 求lim. x?0(x?x2sinx)
解 原式?limx?01?x2?cosx(x?x)sinx(?x?cosx)22, 由x?0时,sinx~x,?x2?x~2,得
1?x2?cosx11?x2?cosx0原式?lim?lim() 23x?02(x?x2)?xx?020x?x
?12x?sinx012?cosx133li()?li???. 2x?02x?3x202x?02?6x224
xsinx?sin2x例5 求lim. x?0x4
12xsinxx?sinxx?sinx01?cosx01??li()解 原式?li. ?lim()?lim?x?0xx?0x?0x?03x2x3x3063x20
(1?x)(1?x)?(1?x)例6 求lim. x?1(1?x)n?1
1n?1?x(1?x)01()?li?,故 解法一 由lix?1(1?x)x?10?1n1
1?x1?x1?x1111??原式?lim=???. x?11?x1?x1?x23nn!
·26 ·
(1??t)(1??t)?(1??t)解法二 原式设1?x?tlim, n?1t?0t
1?由(1??t)????1?(?t)n?n2
xttt??1t??1. ?1?~?(?t)?(t?0),得原式?limt?0nnn!tn?1?
例7 求lime?(1?x). x?0x
e?e
x?0x22ln(1?x)x2解法一 原式?lim??e2limx?0e2ln(1?x)?2x?1x,
2ln(1?x)且x?0时,?2?0,知ex2ln(1?x)?2x?1~2ln(1?x)?2,得 x
2ln(1?x)?2ln(1?x)?x02原式=?elim??2e2lim() 2x?0x?0x0x
1?1?x12??2elim??e2lim?e2lim?e2. x?0x?0x(1?x)x?01?x2x
解法二 原式?lime?e
x?0x
2
x?022ln1?(x)x0()??limex?002ln1?(x)x1?x?ln1(?x) ?22x ??2elimx?(1?x)ln(1?x)x?(1?x)ln1(?x)02??2elim() 22x?00x(1?x)x
??2elim
例8 求lim(x?021?ln(1?x)?1ln1(?x)?e2lim?e2. x?0x?02xx1?cot2x). 2x
221cos2xsinx?x2co2sxsinx?x2co2sx)(???)?li?li解 原式?lim(2? 2x?0xx?0x?0sin2xx2sinxx4
sinx?xcosxsinx?xcosx? 3x?0xx
sinx?xcosxsinx?lim(?cosx)?2。得 由limx?0x?0xx
sinx?xcosx0cosx?cosx?xsinx2sinx2()?2lim?lim?. 原式?2limx?0x?003x?0x3x33x2?lim
·27·
cos(sinx)?cosx. x?0x4
sinx?xsinx?x?2sisi解 原式?lim 4x?0x
sinx?xsinx?xsinx?xsinx?x~~由x?0时,sin,,sin,得 2222
sinx?xsinx?x?2??1sinx?xsinx?x原式?lim ??lim?43x?0x?02xxx
12x1?cosxsinx?xx?sinx01limlim?()????lim. ?limx?0x?0x?0x?03x2063x2x3x3例9 求lim
例10 求limx(x?2?2x?1?x???32x).
解 原式111?tlim(?2?2?1?) 3?t?0xtttt2
2
?lim?t?0?2t?2?t?102?2t2?t()?lim 0t?0?2tt2?2
?1?t??2t1?t??2t0lim?lim() ??t?0t?02t0t?2t??t2
112111lim(?)?(?1)??. ?t?022242?t2?2t?
lnxln(1?x). 例11 求lim?x?1
1
?lnt?t?limt?0. ln(1?t)lnt?lim?tlnt?lim()?lim解 原式令1?x?tlim?1????t?0t?0t?0t?01t?0??t?2t?
ex
例12 求lim100. x?0x
1t50?50!解 原式设2?tlimt()用50次洛必达法则limt?0. t???et???e?x?12
·28 ·
sinxx2
例13 求lim().
x?0x
?
sinx???
?1)?解法一 原式?lim??1?(
x?0x????
sinx?x0lim()x?00x1
sinx
?1x
1
?????
(
sinx1
?1)2xx
?e?ex?0
lim
cosx?13x
?e
1
?x2
lim2()x?03x0
?e
?
16
.
xcoxs?sinxli2
x?02xsinx
ln
解法二 原式?lime
x?0
sinx
x(0)20x
?e
lnsinx?lnx0
()
x?00x2lim
?e
6x2
coxs1
?lix?02x
?e
lim
?e
例14 求lim(sin
x??
xcosx?sinx?0?
??
x?02x3?0?lim
?e
x?0
lim
cosx?xsinx?cosx
?e
?sinx
x?06x
?e
?
16
.
21?cos)x. xx
1
1ln(si2nt?cost)
解 原式令?tlim(sin2t?cost)t?lime
t?0t?0xt
?e
t?0
lim
liln(s2itn?cots)?t?0si2nt?cots
()?e?e2.
t?
2co2st?sitn
?1?
例15 求lim)?.
x?0???x?
xlnln?1?0x
解 lim )(?)?lime??x?0??x?0x??
lnlntlim1
设?tlimet?et???
t???x
1
lnlnt?
()t?
1
t???tlntlim
x
x1
?e
?e0?1.
x例16 求lim?
x?0
sinx
.
x?0?
解 limx?
x?0
sinx
?0??e
limsinxlnx
?e
x?0?
limxlnx
?e
lnx??????1?x?0x???lim
x?0?
lim
?e
?
1
xx?e
?limx
x?0?
?e0?1.
·29·
ex?e2x???enx
x例17 求lim(). x?0n
ex?e2x???enx
x?解 lim()(1) x?0n
ln(e?ex2z11
?ex?0lim???exnxex?2e2x???nenxlim)?lnn0x2xnx()?ex?0e?e???e
?e1?2?3???n
n?en(n?1)
2n?en?1
2.
?1tf(xt)dt. 例18 设f(x)在x?0的某邻域内连续,f(0)?0,f?(0)?2,求lim0
x?0x
解 ?0tf(xt)dt令xt?u?01xu11xf(u)du?2?0uf(u)du,于是 xxx
x?ouf(u)du0f(x)?f(0)12xf(x)f(x)1?lim?f(0)?原式?lim()?lim?lim= 32x?0x?0x?0x?03x3303xx3x
2x?sinx. x??3x?cosx
2x?sinx?2?cosx()?lim(极限不存在),分析 因为lim所以洛必达法则不适用,宜改x??3x?cosx?x???3?sinx例19 求lim
用其它方法。
12?sinx2?02x解 原式?lim??. x??13?033?cosxx
ex?cosx例20 求limx. x???e?sinx
ex?cosx?ex?sinx?ex?cosx?分析由于limx)?limx)?limx)??, x???e?sinx?x???e?cosx?x???e?sinx?
无限循环,所以不能用洛必达法则.
1cosxx1?0解 原式?lim??1. x???11?01?xsinxe1?
2.利用泰勒公式求函数极限。
·30 ·
若f(x)?Axk?o(xk),A?0常数(x?0),则f(x)~Axk。事实上,
f(x)Axk?o(xk)1o(xk)lim?lim?lim(1??k)?1. x?0Axkx?0x?0AxAxk
因此,利用带有佩亚诺余项的泰勒公式可以求出某些函数极限,当x?0时,若
f(x)?Axk?o(xk)~Axk(A?0).
g(x)?Bxm?o(xm)~Bxm(B?0). ??,?kf(x)Ax?A则lim?limm??,x?0g(x)x?0Bx?B
?0,?
cosx?e
x?0x4
?x2
2?x22k?m,k?m, k?m.例21 求lim. 解 由于cosx?ex2x4x21x4
4?(1???o(x))?(1???o(x4), 2!4!22!4
?x2
2(1141cosx?e?)x?0(x4)~?x4(x?0),所以 limx?04!812x414x1. ?lim??4x?012x?
对于求x?x0时的函数极限,若用泰勒公式求极限,可令x?x0?t,变成求t?0时的t的函数极限,再利用上述的方法去解决。
3.利用夹逼定理求函数极限。
x[]. 例22 求lim?x?01x
解 1?1?1?1????,且x?0,两边同乘x以,得1?x?xxx??
?1?
???1?x???1. ?x?(1?x)?1,lim1?1,根据夹逼定理知,lim由limx?1. x?0?x?0?x?0??x?
例23 求limx?0sintdt
x???x.
分析 本题虽然属于"?"型,但不能用洛必达法则,因为 ?
·31·
x???limx?0sinxdtx?limsinx不存在。 x???
因此,用其它方法,
n?解 对任意自然数 n,有 ?0sintdt?n???2n, 0sintdt
x?0sintdt2(n?1)2n当n??x?(n?1)?时,成立不等式 . ??(n?1)?xn?
由lim2n2n22(n?1)2(n?1)2?lim?,lim?lim?.根据夹逼定理知原式x???(n?1)?n??(n?1)?n???x???n?n??
=2
?. 注:这里2n2n,n??x?(n?1)?. 是x的函数,是分段函数,即f(x)?(n?1)?(n?1)?
4.利用定义证明函数极限的存在
利用函数极限定义证明函数极限与利用数列极限定义证明数列极限存在完全类似,在这里我们就不再重复了,一般情况,能不用尽量不用。除非要求用定义证,且考研出这种题的可能性较小。
例24 用定义证明lim?x?1,其中n?N。 x?0
证 不妨设0?x?1,则?x?1?x
(?x)n?1?(?x)n?2???(?x)?1?x,
任给??0,要使?x?1??,由?x??x(0?x?1), 只要x??,取??min? 1,??,当0?x??时,都有?x???,由定义知lim?x?1。x?0
注:这里用了公式(a?b)(an?1?an?2b???bn?1)
?an?an?1b??abn?1?an?1b???abn?1?bn?an?bn。
至于用函数极限的单调有界定理求函数极限的可能性更小。
四、已知函数极限且函数表达式中含有字母常数,确定字母常数数值。
这种题型考的可能性更大,因为这种题型更能考察考生运用无穷小量阶的比较和洛必达法则分析问题,解决问题的能力。
例25 求lim[(x?7x?2)?x]?b?0,求常数a, b. x???54a
解 令1?t,当x???时,t?0?,于是 x
·32 ·
原式?limt?0?[(1t5?7t)a?1?(1?7t?2t5)a1?
4?2t]?limt?0???t5a?t??
?limt1?5a(1?7t?2t5)a?1?b?0, t?0?t
由limt?0?t?0,知分子当t?0时,是分母的同阶无穷小量,所以
tlim1?5a?0??t(1?7t?2t5)a?1??0. 得1?5a?0,即a?1
5,从而 1
?7t?2t5
?lim(1)5
原式?11
5
t?0??lim?1?(7t?2t5)?1tt?0?t
1(7t?2t5)
?lim147t?0?t?5tlim?0?(7?2t)?5。 例26 设limln(1?x)?(ax?bx2)
x?0x2?2,求常数a,b.
1
ln(1?x)?(ax?bx2
解 lim)0?(a?2bx)
x?0x2(0)?limx?02x?2, 由lim2x?0,知分子是分母的同阶无穷小量,得?1x?0limx?0??1?x?a?2bx????0?1?a.
11
有a?1,于是lim?1?2bx
x?02x(0?2?2b
0)?lim(1?x)
x?02?2??1?2b
2, 解得b??5.故a?1,b??5
22。
例27 试确定常数k1c,使得当x???时,arcsin(x2?x?x)~c
xk。
解 由题意知arcsx(2?x?x)
xl?i??c?1. xk
由于arcsin(x2?x?x)=arcsinx
x2~x?x?xx2 ?x?x
33· ·
?x?x1?1
x3
2~?111?(x???), 21x2
11?122x2?x?x)1xkx所以lim?lim?lim1?1, x???x???xcc2c???2xxkxk
1111?1,因此c?,k?. 必有k?,此时,22c22
?
例28 已知limx?01f(x)?1xkx?0?c?0,c为常数,求常数a和k,使时,??fx~ax. 2x
?
解 lix?01f?x??1xx2?0,知 ?c,由limx?0x
lim(?x?01f(x)f(x)?1)?0,必有lim?0,从而 x?0xx
1f(x)?1x?limx?0x21f(x)f(x)x?lim3?c(常数), x?02x12x(?f(x)?1)x?limx?0
得limx?0f(x)3?1,即f(x)~2cx,所以k?3,a?2c. 32cx
例29 确定常数a,b,c的值,使limax?sinx?c?0, 3x?0ln(1?t)x?bdtt
解 由x?0时,ax?sinx?0,且极限c?0, 知分子、分母是同阶无穷小量有
ln(1?t3)lim?dt?0,必有b?0.由于 x?0txblimax?sinx0a?cosxa?cosx()?lim?lim?c?0, 332x?0x?0ln((x?00ln(1?t)1?x))xx?0dttx
·34 ·
且limx?0,知lim(a?cosx)?0?a?1,得a?1,从而 x?0x?02
12x1?cosx1lim?lim??c 22x?0x?02xx
1故a?1,b?0,c?, 2
ln(1?t3)1?t3)0ln(dt??bdt?0 (1) 注:lim?x?0ttx
b
必有b?0,因为b?0,
ln(1?t3)1?t3)0ln(t?[b,0]时,ln(1?t)?0,t?0,有?0,有?bdt?0 tt3
与(1)矛盾,若b?0.
ln(1?t3)1?t3)1?t3)0ln(bln(lim?dt??bdt???0dt?0与(1)矛盾。 x?0tttx
b
故b?0。
例30 设f(x)在x?0存在二阶导数,且 limf(x)?4,求f(0),f?(0),f??(0)。 x?01?cosx
分析:这里表面上没有字母常数,实际上f(0),f?(0),f??(0) 就是待求的字母常数。 解法一 由limf(x)f(x)f(x)?lim2?4,得li2?2. x?0xx?01?cosxx?0x
2
x?0由limx?0,得limf(x)?0?f(0)(f(x)在x?0处连续)。于是 x?02
limx?0
x?0x?0f(x)0f?(x)()?lim?2。 2x?002xx由lim2x?0,得limf?(x)?0?f?(0)(f?(x)在x?0处连续)。从而
limx?0f?(x)1f?(x)?f?(0)1?lim?f??(0)?2, x?02x2x2
得f??(0)?4,
注:求f??(0)时不能用下述方法,limx?0f??x??0?f??(x)f???0?,?f???0??4。虽?2????limx?02x?0?22
然结论对了,但过程是错的。因为f??(0)存在,推不出在x?0的某空心邻域内f??(x)存在且f??(x)
·35·
在x?0不知是否连续,所以limf??(x)?f??(0)。 x?0
解法二 由lix?0f(x)?2, 2x
利用在x?0处的带有二阶余项的佩亚诺展开式,得
f(0)?f?(0)x?
limx?0xf??(0)2x?0(x2)2limx?0,得 由?2.2x?0
f??(0)2??lim?f(0)?f?(0)x?x?o(x2)??0?f(0). x?02!??
f?(0)x?
从而limx?0f??(0)2f??(0)x?0(x2)f?(0)?x?o(x)?lim?2 2x?0xx
f??(0)?x?o(x)??0?f?(0)。于是 2?又limx?0,得lim?f?(0)?x?0x?0??
f??(0)x?o(x)f??(0),所以f??(0)?4. lim?2?x?0x2
五、判断函数极限不存在的方法。
??x0,limxn???x0,limf(xn?)?A,limf(xn??)?B,且A?B,则 1.若limxnn??n??n??n??
极限limf(x)不存在。 x?x0
例31 讨论极限limsinx. x???
??2n?,limxn????,limsin2n??lim0?0, 解 取xnn??n??n??
???2n??取xn
x????2?????,limsin(2n??,limxnn??n???2)?lim1?1, n??而0?1,知limsinx不存在。
2.若limxn?x0,limf(xn)??,则极限limf(x)不存在. n??n??x?x0
sin
例32 讨论极限limx?0x1.
·36 ·
sin
1
2n??112n???lim(2n???)???, n??2解 取xn?2,limxn?0.limn??n??12n??2
sin
知limx?0x1x不存在。
六、关于函数连续性的应用和间断点的讨论。
1.函数连续性的应用
例33 设f(x)在区间X上的连续,且在有理点处都等于0,则f(x)?0。
证?x0?X,取有理数列?rn?,使rn?x0,由f(rn)?0,根据归结原则知limf(rn)?f(x0)?0,故f(x)?0。 n??
例34 若f(x)在区间X上连续,当r1,r2?X且r1?r2,其中r1,r2为有理数,f(r1)?f(r2),则f(x)在区间X递增。
证?x1,x2?x,且x1?x2,取有理数列?rn??,rn??x1,使limrn??x1,取有理数列n??
?rn???,rn???x2,使xlimrn???x2.由rn??x1?x2?rn??, 根据条件有f(rn?)???,
由于f(x)在x?x1处连续,根据归结原则知 f(rn??).(1)
limf(rn?)?f(x1),limf(rn??)?f(x2),在不等式(1)中,令n??,得f(x1)?f(x2)。 n??n??
所以f(x)在区间X是递增函数。
注:这里区间X可以是闭区间、开区间、半闭半开区间或无穷区间。
例35 设f(x)在?a,b?上连续,x1,x2,?xn??a,b?,若
?1,?2,??n?0且满足?1??2????n?1,证明:存在一???a,b?,使
f(?)??1f(x1)??2f(x2)???nf(xn)。
证 由f(x)闭区间?a,b?上连续,则f(x)在?a,b?一定能取到最小值m,最大值M,且值域 ·37·
R(f)?[m,M],又x1,x2,?,xn?[a,b],有
m?f(x1)?M,m?f(x2)?M,?m?f(xn)?M,
又?i?0(i?1,2,?n),且?1??2????n?1,于是
m?m(?1??2????n)??1f(x1)??2f(x2)????nf(xn)?(?1??2???n)M?M。 故至少存在一点???a,b?,使得?1f(x1)??2f(x2)????nf(xn)?f(?)。
例36 证明:若函数f(x)在?a,b?上连续,且对任何x??a,b?,存在相应的y??a,b?, 1f(y),则f(x)?0。 2
1f(y1),同样存在y2??a,b? 证 ?x0??a,b?,由条件知存在y1??a,b?,使f(x0)?2
111f(y1)?2f(y2),如此下去?,存在数列?yn???a,b?,使f(x0)?nf(yn),使f(x0)?222使得f(x)?
由f(x)在?a,b?上连续,则f(x)在?a,b?上有界,于是存在M?0, 对于一切x?[a,b],都有f(x)?M,从而f(x0)?1M。 2n
令n??,得f(x0)?0?f(x0)?0?f(x0)?0,由x0是?a,b?上任意一点,故f(x)?0。
例37 设f(x)在R上有定义且在x?0,1两点连续。证明:若对任何x?R,都有f(x2)?f(x),则f(x)为常值函数。
证 (i)当x?1时,由条件得
f(x)?f(x2)?f(x4)???f(x2n),知f(x2n)是常值数列。
又limxn??2n???0,且f(x)在x?0处连续,由归结原则,f(x)?limf(x2n)?f(0) n??
(ii)当x?1时,由条件得
111??????2222422f(x)?f(x)?f?(x)??f?(x)????f?(x)?是常值数列。 ????????
由x2?1,得1?(x)1
22n?(x)1
2n,而lim1?1,lim(x)?1,知lim(x)n??n??n??21n212n?1,且
·38 ·
?221n?f(x)在x?1处连续,根据归结原则知f(x)?limf?(x)??f(1). n????
f(x)?f(1)?f(0), 由0?x?1时,f(x)?f(0),知lim?1x?1
f(?1)?f(?1)2?f(1),知?x?R.都有f(x)?f(0),x?R。
2.间断点的讨论
如果f(x)是初等函数,若f(x)在x?x0处没有定义,但在x0一侧或两侧有定义,则x?x0是间断点,再根据在x?x0处左右极限来确定是第几类间断点。如果f(x)是分段函数,分界点是间断点的怀疑点。 ??
sintsint?sinx例38 求极限lim(,记此极限为f(x),求函数f(x)的间断点并指出其类型。 )t?xsinx
?t??sin?1??1解 f(x)?lim?t?x?x??sin???sinxsitn?sinxx?????xsinx?exsinx,
由于f(x)在x?k?处没定义,而在k?两侧有定义,故x?k?是间断点。 x
sinx又limf(x)?limex?0x?0?e,所以x?0是函数f(x)的第一类(可去)间断点。
x?k?(k??1,?2,?)是f(x)的第二类(无穷)间断点。
例39 讨论f?x??e的间断点,并指出间断点的类型。 1
x
e???,lime?0,所以x?0是第二类间断点。 解 由于f(x)在点x?0处无定义且lim??x?0x?01x1x
x?etx
例40 讨论f(x)?lim的间断点,并指出类型。 t???1?etx
?x,x?0,??1解 由于f(x)??,x?0,知x?0时,f(x)显然连续. 2??1,x?0.?
·39·
f(x)?limx?0,limf(x)?lim1?1.0?1,所以x?0是跳跃间断点。 且lim????x?0x?0x?0x?0
七、关于分段函数在分界点连续性的讨论。
?a?bx2,x?0,?在x?0处连续,求常数a与b的关系。 例41 设f(x)??sinbx,x?0??x
解 由f(x)在x?0处连续 ,知f(x)在x?0处既是左连续又是续右。连
2limf(x)?lim(a?bx)?a?f(0)?a, ??x?0x?0
x?0limf(x)?lim??x?0sinbxbx?lim?b?f(0)?a,故a?b。 x?0?xx
注:由x?0,即x?(??,0]时,f(x)?a?bx2是初等函数表达式。在x?0处有意义知连续且为左连续,以后遇到类似情况,我可直接得出左连续,从而只要右连续即可。
1?2?(cosx)x,x?0
?例42 已知f(x)??在x?0处连续,求常数a.
?x?0?a,
?
1cosx?11
2解 因为limf(x)?lim(cosx)x
x?0
1
2x?0??lim??1?(coxs?1)?x?0?1cosx?1???x?e??f?0??a。 所以a?e?。
八、杂题
例43 若limsin6x?xf(x)6?f(x)?0,求lim。 32x?0x?0xx
(6x)3
6x?6x??o(x3),故 解法一 由于sin3!
lim
从而limsin6x?xf(x)?6?f(x)??lim?36?0 32??x?0x?0x?x?6?f(x)?36。 x?0x2
6?f(x)6x?xf(x)?li解法二 li x?0x?0x2x3
·40 ·
sin6x?xf(x)6x?sin6x6x?sin6x0?)?lim() x?0x?00x3x3x3
1(6x)2
6?6cos6x?lim?2lim?36. 22x?0x?03xx
f(u)d?A,求lim?1例44 设f(u)在u?0的某邻域内连续,且lim0f(xt)dt. u?0x?0dxu?lim(
x?0f(u)du11,又 解 令xt?u,dt?du,得?0(xt)dt?xx
xxf(u)duxf(x)??0f(u)dud1d?0?0f(xt)dt?()?, 2dxdxxx
x?0f(u)du0AAf(x)A?A??。 ()?lim?于是 lim, 故 原式0x?0x?02x222x2
例45 设f?(0)?0,f??(0)存在,证明lim?x?0f?x??f?ln?1?x??1?f???0?. 32x
证:由f??(0)存在,知??0?0,当x??0,?0?时,f?(x)存在。当x充分小时,?ln(1?x),x???0,?0?,在?ln(1?x),x?上对f(x)应用拉格朗日定理得f(x)?f(ln(1?x))?f?(?x)(x?ln(1?x)),其中ln(1?x)??x?x。
f(x)?f(ln(1?x))f?(?x)(x?ln(1?x))lim?limx?0?x?0?x3x3
?lim? x?ln(1?x)f?(?x)?f?(0)?x ??2x?0?xxx
f?(?x)?f?(0)?f??(0), 由x?0时,ln(1?x)?0,知?x?0,有limx?0?x
ln?1?x??xln?1?x??x??1,且lim?1,由夹逼定理知lim?1. x?0x?0xxxx
而 limx?0x?ln(1?x)0()?limx?00x21?1x1?lim?, x?02x(1?x)2x2故 lim?f(x)?f(ln(1?x))??f??(0). x?02x3
tan(tanx)?sin(sinx)例46 求lim. x?0tanx?sinx
·41·
分析 这题虽然是“0”型,但直接用洛必达法则或等价量替代,都不能求出结果。然而从被0
求的式子构成形式,启发我们用微分中值定理
解原式 ?limtan(taxn)?tan(sixn)?tan(sixn)?sin(six)n x?0tanx?sinx
tan(tanx)?tan(sinx)tan(sinx)?tan(sinx)cos(sinx)?lim?lim x?0x?0tanx?sinxtanx?sinx
tan(sinx)1?cosx(sinx)?limsec2?x?lim? x?0x?0tanx1?cosx
12sinxsinx2?limsec?x?lim??1?1?2. ?x?0x?012xx2
sinx?0,tanx?0,注:由于?x介于sinx,tanx之间,当x?0时,根据夹逼定理知?x?0
ex?esinx
例47 lim. x?0x?sinx
e解原式 ?limx?0sinxxex?sin?1?1?1?1. x?sinx
注:此题也可用微分中值定理去求。
·42 ·
第三节 数列极限
数列极限内容网络图
数列极限的定义
直接证法
用定义证明数列极限的方法
间接证法 唯一性 有界性
收敛数列的性质
不等式 保号性 四则运算
夹逼定理
判断数列收敛的准则
数 单调有界定理
列 极 两个子列极限存在但不相等
限
判断数列发散的准则
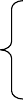
有一个子列发散 数列无界
lim1
n??
n
k?0(k>0常数) limnn??
q?0(|q|<1常数)
limn??
a?1(a>0常数) lim重要的数列极限
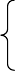
n??n?1
lim(1?1
n??
n
n?e
limlnnn??
nk?0?k?0常数? n
k
limn??a
n?0?a?1,a,k为常数?
43·
§3.1
·
§3.2 内容提要与释疑解难
一、数列极限的概念
定义 设{an}是一个数列,a是一个确定的常数,若对任意给定的正数ε,总存在一个自然数N,使得n>N时,都有an?a??,则称数列{an}的极限是a,或者说数列{an}收敛于a,记作lim n??an?a。
注意:
1. ε的任意性,ε的作用在于衡量an与a的接近程度,从而限制ε小于某一个正常数,不影响衡量an与a接近的程度,但不能限制大于某一个正常数,定义中的ε可用2ε、或ε2等本质上是任意的正常数来替代,同样也可把“<”号换成“≤”号。
2. N的相应性。一般说,N是随着ε的变小而变大,但并不是由ε唯一确定,因为给定ε,确定N,当n>N,有an?a??,则N+1,N+2,?同样也符合要求。此外,n>N中的N只是下标的一个界线,要求n是自然数,故N可以是实数,而且n>N也可改成n≥N。
3.几何意义:lim表明a的任何给定的ε邻域中都含有数列{an}中除了有限项以外的全n??an?a,
有项。
二、收敛数列的性质
性质1 (唯一性)若数列{an}极限存在,则极限值是唯一的。
性质2 改变数列的有限项,不改变数列的收敛性与极限。
有了性质2,对于判定数列敛散性的定理中要求从第一项就具有某种性质的条件可减弱为从某一项开始具有该性质,结论依然成立。
性质3(有界性)数列{an}收敛,则{an}为有界数列,即存在某正常数M,使得对一切正整数n,都有an?M。
推论 若数列{an}无界,则数列{an}发散。
该推论是判断数列{an}发散的一个简单有效的办法。
lim性质4 设lim则存在N0,当n>N0时(即n充分大时),都有an<bn。 n??an?a,n??bn?b且 a<b,
推论(保号性),若lim
n??an?a?0(a?0),则对于满足0<η<a(a<η<0)的任何常数η,存在
N,当n>N时,都有an>η>0(an<η<0)。
性质5(不等式)若n??an?a,n??bn?b,且存在N0,当n>N0时,都有an≥bn,则a≥b. 注意在性质5中,即使存在N0,当n>N0时,都有an>bn,也不能保证a>b.
例如 an?limlimlim11,bn??,an>bn(n=1,2,?), nn但n??an?0,n??bn?0,而0=0。
性质6 数列{an}收敛的充要条件是:数列{an}的任何一个子数列都收敛且极限相等。 ·44 · lim
逆否定理 若数列{an}有两个子数列极限存在不相等或有一个子数列极限不存在,则数列{an}发散。
该定理是判断数列{an}发散的一个重要方法。
lim性质7 (数列极限的四则运算)若lim
n??an?a,n??bn?b,则数列{an±bn},{anbn},??an??b?n?
(b≠0)的极限都存在,且
limlimlimlimlim(1)lim
n??(an?bn)?n??an?n??bn?a?b; (2)n??(an?bn)?n??an?n??bn?a?b;
lim特别地,当k为常数时,有lim
n??kan?kn??an?ka;
(3)lim
n??an?bnlinn??limn??ana?bnb(b?0).
注意:数列极限的四则运算前提是两个数列极限都存在,并可把数列极限推广到有限项极限的四则运算,但数列极限的运算法则不能推广到无限项.
例 n???
lim1?1lim11?11lim??????1?lim?????0。 n??n??n??nnnnnn??
§3.3 解题方法与技巧
一、求数列极限的方法
1.利用数列极限定义证明数列极限存在
要证lim
n??an?a,即证明???0,?N,当n>N时,都有an?a??.由定义可知,n>N是an?a??成立的充分条件,从而有
(1)直接证法(充要条件)
???0,找出使an?a??成立的充要条件(当然也是充分条件)n?N(?),即和中学解一般不等式的方法相同,由an?a???n?N???。
n例1 证明 lim
n??q?0(|q|<1,且q为常数).
证(i)当q=0时,知q????0?为常值数列,有nlim
n??0?0.
nn(ii)当0?q?1时,???0,要使q?0???q???lnq?ln??nlnq?ln?n
(由lnq为负数)?n?ln?ln?nn,取N?,当n>N时,都有q?0??,所以lim
n??a?0,lnqlnq
·45·
n总之lim
n??q?0。
(2)适当放大法(充分条件)
有时从an?a??中等价解出n?N???很困难。这时我们就可用适当放大法,使得
。只要g?n????n?N2(?),取N?max?N1,N2????,当n>N时,有an?a?g(n)(n?N1)
an?a?g?n???。
在使用适当放大法时,我们要求:
①放大以后的g(n)要尽可能简单,从g(n)<ε中等价解出n>N2(ε)容易 ②lim
n??g(n)?0,即放大以后的式子必须以0为极限 (a)直接放大,把an?a化简一步一步放大,使an?a?g?n??n?N1?. (b)间接放大,有时从an?a直接放大不容易,我们可借助于其它公式如二项式公式及各种不等式等辅助工具来达到放大的目的。
例2 证明
证 设 limn??n?1。 n(n?1)2nhn???hn 2nn??n?1?hn,可得n??1?hn??1?nhn?
?1?
可推出hn?2n(n?1)2hn(n?1), 22,即hn?n2,于是nn?1?2.所以,???0,要使nn?1??,只要
222?2??????2?n?2,取N?max?1,2?,当n>N时,都有nn????limn??n?1??,所以n?1.
2.利用重要数列极限和极限四则运算求极限
例3 求lim
n??a0nm?a1nm?1???am?1n?am kk?1b0n?b1n???bk?1n?bk
111???aam?1m?1mmnmn ?111nkb0?b1???bk?1k?1?bkknnna0?a1其中a0,a1,?,am,b0,b1,?,bk均为常数且a0≠0,b0≠0。 解 原式?n??lim
·46 ·
?0,??a ??0,
?b0
???,m?k,m?k, m?k.
这个例子表明当分子最高次幂小于分母最高次幂时,分式极限为零;当分子最高次幂等于分母最高次幂时,分式极限就是分子、分母最高次幂的系数之比;当分子最高次幂大于分母最高次幂时,分式的极限为?,以后该例题的结果可以作为结论用,同理可证对分子、分母的每一项幂指数是正数时结果仍成立,例如。
lim
n??2n?2n?4n?5
3n?7n?2n?64
31243132?. 3
例4 求 lim
n????n?3n?n?n??. ??
解 原式?n??lim??n?3n?n?n????n?3n?n?n??????
n?3n?n?n
=n??lim4
?3
n??1
n?4?2. 1?1
3. 利用夹逼定理求极限
lim夹逼定理 设{an},{bn}为收敛数列,且lim
n??an?a,n??bn?a,若存在N0,当n>N0时,
都有an?cn?bn,则数列{cn}收敛,且lim
n??cn?a.
夹逼定理适合数列的项有多项相加或相乘式n??时,有无穷项相加或相乘,且不能化简,不能利用极限的四则运算,此时可尝试用夹逼定理。夹逼定理不仅能证明数列极限并可求出极限的值。
例5 求极限 limn??na1?a2???am,其中a1,a2,?,am均为正常数 nn
解 不妨设a1?ma?xa1,a2,?,am?,由于
na1?a1?a2???am?m?a1?a1m, nnn
且lim
n??a1?a1,
lim
n??nnlimn??a1m?a1,由夹逼定理知. na1?a2???am?a1?max?a1,a2,?,am?.
例6 求
limn????1?n?a?na??0?a?1且为常数?. ·47·
解 由 0??1?a?
limlim
n??a??1?a???1??1?n?n??1???1??na??1???1??1?a, ??n??n????n??aa且n??0?0,
例7 1n1?aa?0(1-a>0且为常数),根据夹逼定理知lim1?n??na?0. n?????lim求n????2n(n?1)?2?3??. ????2?n2?1n2?2n?n???
解 设In?n(n?1)?22?3,由于 ????222n?1n?2n?n
12nn?n?1?1??????, 222n?nn?nn?n2n(n?1)2In?
In?
11?,2223n?1(n?3)n?????, n2?1n2?1n2?12(n2?1)lim
n??且n??limn(n?3)1?,根据夹逼定理知 22(n?1)2
lim
n??In?lim,
n??((n?1)?22?31????)?. 2222n?1n?2n?n
1352n?1???. 2462n
1352n?12462n????解 由于???,所以 2462n3572n?1例8 求n??lim
132n?1242n11?132n?1? ???????, ????2n?242n352n?12n?1n?24
即 0?2132n?11???, 242nn
且n??0?0,limlim
n??1n?0,由夹逼定理知
lim
n??132n?1???0. 242n
lim例9 u1?1,u2?2,当n≥3时,un?un?1?un?2,求n??
解法一 由条件知{un}递增,知
·48 · 1。 un
un?un?1?un?2?un?1?un?1?2un?1
13un?un?1?un?2?un?1?un?1?un?1 22
?3??3?从而 un???un?2????2??2?
且lim
n??0?0,lim?2?
n?????3?n?12n?1?3?u1????2?n?11?2?, 得 0????un?3?1?0. unn?1 ?0,根据夹逼定理知limn??
解法二 由条件知un>0,显然{un}递增,知??1??1?1递减,且,由单调有界定理知?0???收uun?n??un?敛,设lim11?l,有l?0. 若不然l?0, 有limun?, n??n??uln
111??, lll又un?un?1?un?2,令n??,有
得=0,与1
l11?0相矛盾,故假设不成立,所以lim?0. n??lun
2????sinsin?sin??nn例10 求lim??????. n??n?111?n?n???2n???
?2?sisi?n?n???sin解 设In?,由 11n?1n?n?2n
n1?2?n?1ni?1i?In?(sin?sin???sin)??sin??sinnnnnni?1nni?1n
1?2?n?In?(sin?sin???sin) n?1nnn
n1ni?nn1i????sin?sin.?n?1ni?1nn?1i?1nn
在和式111i?1?1??x?,有b?a?n??1f(x)?sin?x中,。, sin???a,a?i?1??nnnnnn??i?1n
令n??,0?[a,a]知a?0,b?1且f(x)在[0,1]上连续必可积。而
1i?是f(x)在sin?ni?1nn·49·
[0,1]上,把区间[0,1]n等分,?i取每个小区间左端点得到的和式,由定积分定义知
1n1ni?21i??1?12lim?sin??sin?dx???cos?x?0? ,且lim??sin?,根据夹逼定0n??n??n?1ni?1n?n????i?1nn
2?
????sin?]?2。 理知limIn?lim[n??n??n?111?n?n?2nsinsin
xn
例11 求lim?dx. n??1?x
xn112解法一 由0??dx??0xndx??()n?1, 1?xn?12
11n?1xn
2?()=0,根据夹逼定理知 lim?0且lim0=0,limdx=0。 n??n??n?1n??21?x11201120?
?nn11xn
解法二 由?dx=?,其中0??n?, 21?x1??n2
而120211为有界量,又 ??1,知31??n1??n
10??nn?()n,根据夹逼定理知lim?nn?0。 n??2
从而原式?limn??2?1??nn?0(有界量乘以无穷小量仍是无穷小量). 1??n
4.利用单调有界定理证明数列?an?递增(递减)有上界(下界),则数列?an?收敛,即单调有界数列有极限。
单调有界定理适合数列的项用递推关系式给出的数列。单调有界定理仅能证明数列极限存在,至于数列极限的值是多少只能用别的方法去解决。
例12 设c?0为常数,证明xn?
分析 由于xn?1?c?c???c极限存在,并求limxn。 n个根号n??c?xn,容易观察出?xn?是递增的,并可用数学归纳法证明。关键是证明它有上界,哪一个数是?xn?的上界呢?我们观察不出来。由于?xn?是递增的,所以,若?xn?极限·50 ·
存在,则极限值一定是它的一个上界,若?xn?有极限,设limxn=a,由于xn?1?n??c?xn, 令n??,有a?c?a,两边平方得a2?a?c?0,解得
a?1??4c1??4c。由题意知a?0,所以a?,由于a太复杂,我们对它作适当放大,22
有a?1??4c?4c1?(1?2c)??1?c,则必有xn?1?c。 22
c?x2?c?c,即n?1证 显然xn?0,我们先证?xn?递增的,即xn?xn?1。由于x1?
时不等式成立。假设n?k时,xk?xk?1成立。当n?k?1时,由xk?xk?1,
?0?c?xk?c?xk?1?c?xk?c?xk?1?xk?1?xk?2,即n?k?1时不等式也成立,由数学归纳法知xn?xn?1,知?xn?递增。再证?xn?有上界,用数学归纳法证明:由x1?假设c?1?c,时, n?k时,xk?1?c,当n?k?1xk?1?c?xk?c?1?c?c?1?2c?1?c。即n?k?1时也成立,由数学归纳法知对一切n?N,都有xn?1?。根据单调有界定理知?xn?收敛。 由xn?1?设limxn?a.n??c?xn,令n??,有a??a?a2?c?a?a2?a?c?0,解得a?1??4c,知a?0, 2
知a?1??4c1??4c1??4c,由条件知a?。知limxn?。 n??222
在上题证明了数列有界时,我们也可用下面方法证。
我们已经证明了?xn?严格递增,即
2xn?xn?1?c?xn?xn?xn?c?0?1??4c1??4c1??4c,故xn?。?xn?222
从而?xn?有上界。
注:在求由递推关系式给出数列的极限时,一定要先证明数列极限存在,再求极限,否则就犯了逻辑性错误。
·51·
例如 数列(?1)n是发散的。如果我们不去判断它的收敛性,直接求极限会怎么样呢?设??
an?a,令n??有a??a,即2a?0得a?0,于是an?(?1)n,an?1?(?1)n?1??an,设limn??
lim(?1)n?0。这里犯错误的原因是没有证明an的极限是否存在,便假设liman?a。在错误的假n??n??
设下,当然推出错误的结论。因此,一定要证明?an?收敛后,再设liman?a。 n??
32xn?1?1例13 设x0?2,xn?,(n?1,2,?)证明limxn存在,并计算此极限。 2n??3xn?1
31?xn2?1,且3xn??1?0,所以要判断?xn?是否单调,关键是判断分式的23xn?1分析 由于xn?xn?1
分子中x3
n?1与32xn?1?11之间的大小,即xn?1与1之间的大小。若?xn?收敛,设liman?a,对xn?,2n??3xn?1
2a3?1令n??有a?解得a=1,若xn?1,则xn?xn?1?0。即?xn?递减,若xn?1,则?xn?递23a
增。
32xn111?1?1?(x?x?)?x?x?1,证 由于xn?所以?xn?有下界,而 n?1n?1n?1n?1223xn?1xn?13xn?1
31?xn?1??0。 23xn?1xn?xn?1
32xn?1?1知?xn?递减。由单调有界定理知,?xn?收敛,设liman?a,对xn?,令n??有2n??3xn?1
2a3?1a?,解得a?1.因此limxn?1。 2n??3a
例14 设xn?sinsin?sinx(x为常数)。求limxn。 ???????n??n个
解 设an?xn?sin sin?sinx,由不等式sinx?x且等号仅x当?0时成立知
又an?0,从而?an?递减有下界,故?an?an?1?sinsinsin?sinx?sinsinsin?sinx?an,
n?1个n个
收敛。
设liman?c,由于an?1?sinsinsin?sinx?sinsinsin?sinx?sinan n??n?1个n个
·52 ·
令n??,有c?sinc,且c?0,c?sinc,由前面不等式性质知c?0。知liman?limxn?0,所以limxn?0。 n??n??n??
nk
xn. 例15 设xn?n(a?1为常数,k常数),求limn??a
a解 设an?xn,lim?n?1?limxn??n??an?n?1?kanka1?limn??a1?1???1????1 a?n?k
由极限的不等式性质知,存在N0,当n?N0时,都有an?1?1或an?1?an, an
11(1?)kan,令an知?an?递减且an?0。由单调有界定理知?an?收敛,设liman?c,由an?1?n??
n??,有c?1?c,化简有(a?1)c?0,由a?1?0,得c?0,知liman?0,故limxn?0. n??n??a?xn(b?0),n?1,2,?,证明?xn?收敛于方程x2?x?b?0的例16 设x1?a?0,xn?1?
正根。
证(i) 若a?a?b,由x1?a?a?b?x2,
假设n?k时,xk?xk?1?0成立,当n?k?1时,b?xk?b?xk?1?0, 两边开二次方根有xk?1??xk??xk?1?xk?2,
即n?k?1时,不等式xk?1?xk?2成立,由数学归纳法知?xn?递减且xn?0,根据单调有界定理知?xn?收敛。
(ii)a?a?b,由x1?a?a?b?x2
假设n?k时,xk?xk?1成立,当n?k?1时,0?b?xk?b?xk?1, 有xk?1?
增。
下面再证?xn?有上界,由
b?xk?b?xk?1?xk?2,即n?k?1时,xk?1?xk?2成立。由数学归纳法知?xn?递·53·
2
?xn?b?0?xn?xn?1??xn?xn
1??4b1??4b1??4b
。 ?xn??xn?
222
即?xn?有上界,故?xn?收敛。
设limxn?c,由xn?1?
n??
?xn,令n??,有c??c?c2?c?b?0且c?0,故?xn?收
敛于x?x?b的正根。
例17 证明xn?(1?
2
111
)(1?2)?(1?n)收敛。 222
12
n?1
解 由于xn?1?xn?(1?
)?xn,知?xn?递增,又xn?e
1
11?2
lnxn
?e
111ln(1?)(1?2)?(1?n)
222
?e
111
????n2222
?e
111
????n??2222
?e?e。
知?xn?有界,由单调有界定理知?xn?收敛。
注:1. 此数列虽然我们证明它收敛,但此极限值用上述的方法就求不出来。用其它方法也不好
求。
2. 在证明此数列有界的过程中,用到了不等式当x?0时,4.利用函数极限求数列极限。
由数列?an?中的通项是n的表达式,即an?f(n).而limf(n)与limf(x)是特殊与一般的关
n??
x??
x
?ln(1?x)?x。 1?x
系,由归纳原则知
x???
limf(x)?A(?)?limf(n)?A(?). (1)
n??
反之不一定。
从而,当求极限limf(n)时,若f(n)的极限属于未定式时,对数列极限当然不能用洛比达法
n??
则,因为f(n)作为函数在图象上是离散的点,既不连续,更不可导,但我们可用结论(1),转化为函数极限,对于求函数极限,便可以利用洛必达法则去求,当然也利用求函数极限的其它方法。
例18 求limn[(1?
n??
1n
)?e]. n
1x1(1?t)?e0e)?e]?tlim()?lim
t?0?xxt0t?0?
1
t
ln1?(t)t
解 原式?limx[(1?
x???
?e
t
·54 ·
=lime?
t?0
ln(1?t)
t
t
?ln(1?t)
t?(1?t)ln(1?t)
?lim e??2
t?0?t2(1?t)t
=lime??
t?0
1?ln(1?t)?1et?(1?t)ln(1?t)?0?elim??=. ??
t?0?2t20t2??
n
例19 求limtan(
n??
?
2
?). 4n
x
解法一 原式?limtan(
x???
?
2?) 4x
2
2?t
[tan(?t)] ?tlim?limet?0?t?0?x4
2lntan(?t)
4t
?
?0??? ?0?
?e
t?0?
lim
2ln?t)lim04t?0?
()?e
t0
?
2?t)
4
?
?sec2(?t)?e4.
4
2
?2
?
22ta?ta???nnn
??112???2????2?1?ta22???2tan?n?2?tan?n????????解法二 原式?lim?lim??(1?ta)????(1?ta)???? ?n??n??2nn?1?ta???????????????n??????????????
e2
??2?e4。 e
注:在解法二中利用了函数的重要极限lim(1?x)?e.
x?0
1x
5.利用级数的收敛,求数列极限或证明数列收敛。(此种方法对数学一、三要求,对数学二、四不要求)
(1)若
?a
n?1
?
n
收敛,则liman?0。
n??
n!an
例20 求limn(0?a?e常数)
n??nn!ann!an
解 对于一般级数?n,un?,由 n
nnn?1
?
·55·
limn?un?1un(n?1)!an?1?limn??(n?1)n?1n!a
nnn?lima?n??1(1?1n)n?ae?1, n!ann!an
知?n绝对收敛,因此limn?0。 n??nn?1n?
例21 求lim
?n??11n2(1?). nn4
解 由11n211n2u?(1?), 为正项级数,设(1?)n?nnn4nn?14
limun?limn??n??
?11n211ne(1?)?lim(1?)??1, nn??n4n44
知11n211n2lim(1?)?0. 收敛,因此,(1?)?nnn??n4nn?14
(2)?an?收敛?a0?
??(an?1?n?an?1)
由于?(a
n?1
?n?an?1)前n项和为(a1?a0)?(a2?a1)???(an?an?1)?an?a0,
?an?1)的收敛性等价于?an?的收敛性。若?(an?an?1)收敛,则
n?1?因此?(an?1n
liman?n???(an?1?n?an?1)?a0。
11(x0?x1),?,xn?(xn?1?xn?2),求limxn,其中n??22例22 设x0?a,x1?b,x2?
a,b为任意常数。
分析 由题设条件可看出x1?x0,x2?x1,? 具有递归规律,因此,可考虑用级数求和方法来解。
解 由xn?11(xn?1?xn?2), 得xn?xn?1??(xn?1?xn?2)。 22
11x1?x0?b?a,x2?x1??(b?a),x3?x2?(?)2(b?a), 22
·56 ·
1?,xn?xn?1?(?)n?1(b?a),于是 2
1limxn?a??(?)n?1(b?a)?a?(b?a)n??2n?1?111?(?)2a?2a?2b(b?a)?. 33
6.利用等价量替换来求数列极限。
由于在求函数极限时,可对分式分子、分母中的复杂因式用简单的等价量来替换。而数列也是特殊的函数,故在求数列极限时,也可用等价量替换。
na
例23 已知limb?2003,且a,b.为常数,求a,b。 n??n?(n?1)b
解 limn??na1nb[1?(1?)b]n?na??1?????n??1?(?)??1?n??????bb,
利用 (1?x)b?1~bx(x?0),有 1na?1
?lim?b?2003, 原式?limn??n??b1n?nb?b(?)n
知a?1?b,na112002?2003,解得b?,a??. b20032003
7.利用和式极限化为定积分求数列极限。
例24 求limn??n!. n
1112nln??)lim112nn!n!nnennn=en??ln(??) ?lim(n)?lim解 原式lin??nn??n??nnnnn
=en??limlimn1nii1?1n??ln?e?ln??e0lnxdx?e(xlnx?x)?ni?1nnni?110
?e?1?lim(xlnx?x)x?0?e?1?0?e?1.
1注:因为 ?0lnxdx是广义积分,x?0是瑕点,所以下限x?0代入原函数是指原函数在x?0
处的极限。
二、判断数列极限不存在的方法
1.若数列{an}有两个子数列极限存在但不相等,则{an}发散
·57·
例25 判断数列?sin?
?n???的收敛性 4?
解 取n?8k?2。得子数列?sin?2k???
????????lim?lim?2k????k??1?1, ??,k??sin2?2???
?
?n???发散。 4?lim取n=8k,得子数列?sin2k??,limsin2k??k??k??0?0,由1?0,知数列?sin
2.若数列{an}无界,则数列{an}发散 例26 判断数列??1?n2的收敛性。 n?
n?解 设an???1?n2,?M?0,?n?
{an}无界
·58 · M,有n2?M,知an?n2?M,从而{an}无界,故
