离散数学学期总结
离散数学是描绘一些离散量与量之间的相互逻辑结构及关系的学科。它的思想方法及内容渗透到计算机学科的各个领域中。因此它成为计算机及相关专业的一门重要专业基础课。主要内容包括:集合论、关系、代数系统、图论和数理逻辑五个部分。结构上,从集合论入手,后介绍数理逻辑,便于学生学习。为了能很好的消化理解内容,列举了大量的较为典型、易于接受、说明问题的例题,配备了相当数量的习题,也列举了部分实际应用问题。
一. 知识点
第一章.集合论
集合论或集论是研究集合(由一堆抽象物件构成的整体)的数学理论,包含集合、元素和成员关系等最基本数学概念。在大多数现代数学的公式化中,集合论提供了要如何描述数学物件的语言。
本章主要介绍集合的基本概念、运算及幂集合和笛卡尔乘积。这章是本书的基础部分,要学好离散数学就必须很好的掌握集合的内容。集合论的概念和方法已经渗透到所有的数学分支,因而各数学分支的完整体系,都是在所取集合上。
第二章.关系
关系在我们日常生活中经常会遇到关系这一概念。但在数学中关系表示集合中元素间的联系。本章主要学习关系的基本概念、关系的性质、闭包运算、次序关系、等价关系,本章学习的重点:关系的性质、闭包运算、次序关系。
关系这一章是集合论这一章的延伸,对集合论的理解程度对学习关系这一章是非常有影响的。而关系又是学习下一章代数系统必不可少的,所以本章是非常重要的章节。
第三章.代数系统
代数结构也叫做抽象代数,主要研究抽象的代数系统。抽象代数研究的中心问题就是一种很重要的数学结构--代数系统:半群、群等等。
本章主要学习了运算与半群、群。学习本章需要学会判断是否是代数系统、群和半群,以及判断代数系统具有哪些运算规律,如:结合、交换律等及单位元、逆元。这些都在我们计算机编码中体现出重要的作用。
第四章.图论
图论〔Graph Theory〕起源于著名的柯尼斯堡七桥问题,以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
本章主要学习图的基本概念、路径与回路、图的矩阵表示、平面图和二部图、以及树。学习的重点:图的矩阵表示、平面图和二部图、以及树。
第五章.数理逻辑
数理逻辑又称符号逻辑、理论逻辑。它既是数学的一个分支,也是逻辑学的一个分支。是用数学方法研究逻辑或形式逻辑。数理逻辑是数学基础的一个不可缺少的组成部分。虽然名称中有逻辑两字,但并不属于单纯逻辑学范畴。
数理逻辑与计算机科学有着密切的关系,它已成为计算机科学的基础理论。
本章学习的重点:命题及联结词、命题公式及公式的等值和蕴含关系、对偶与范式、命题演算的推理规则、谓词逻辑简介。
二.学习情况
离散数学作为一门必修课,其地位是非常重要的。学习好这门课对于我们也是颇有益处。而且离散数学还是一门有很深内涵的学科。
集合论是本书的这一章节,我们在以前已经学习过集合,为什么现在还要学习呢,这就足见集合在离散数学这门课程中的重要,把集合的知识作为一个基础的知识点,来作铺垫。所以说要想学习好离散数学就必须先将集合的知识掌握好。
关系是集合知识点的延伸,关系是相对于集合而言的。关系也是一个重要的知识点,对后续知识的学习也有重要的作用。后面的代数系统就必须依赖关系才存在的。如果一个系统里不存在关系,那么这个系统也是不存在的。系统里必然存在某种关系,这才使系统存在有意义。
代数系统的学习是对前面的集合论与关系的以个总结。学习了集合论与关系有什么用,在这一章节我们就可以看出来。通过学习这一章,对前面两章有了更深的理解,也对前面所学知识有了一个总结。但同时本章也是本书中比较难以了理解的章节,在本章的学习中遇到一些问题,但是在同学的帮助下都一一解决了。
图论的学习对于我们计算机专业的学生来说是非常的重要的,因为它与我们计算机专业的关系最密切。在学习中,图不再是我们以前接触的图,而是学习的事如何在点与点之间连结的问题。这对于发散我们的思维有很大的帮助。
数理逻辑是本书最重要的章节,它是培养我们的抽象思维,让我们能在其他学科能够运用一定的思维方式来解决问题。对于计算机专业来说,数理逻辑提高了计算机的工作效率。数理逻辑在计算机专业方面起到了重要的作用。
三.学习体会
学习了离散数学这门课程,对于一个爱好数学的人来说,我是非常受益的。同时,离散数学作为一门与计算机学科相关的专业基础课,对我学专业知识也有很大的帮助。
学习离散数学,可以培养我们的逻辑思维方式,对于我们学习计算机方向的学生来说是非常有用的。尤其是在计算机编程方面对逻辑思维就有一定的要求。离散数学这门课程,是一门比较难学的课程,它有太多的概念、定义,需要我们有很好的记忆力,但是要完全记住这么多的概念、定义是非常困难的。所以说我们在有好的记忆力之外,还要运用理解记忆的方法来解决,这样我们就不必花费过多的时间和精力去记忆这么多的概念和定义了。离散数学作为一门理科学科,在我看来最好的学习方法就是多动手、多做题,在做题得过程中,慢慢积累做题得经验,同时也可以对概念和定义有一个更深层次的理解。
学习各个学科都有其各自的学习方法与思维方式,只有运用对了学习方法才能更好的学习这门课程。学习一门课程都是为了解决实际问题,学习离散数学也不例外。学通了一门课程才能在解决问题的时候不会走弯路。
上面说到了离散数学是一门比较难学的课程,在学习的过程中,也肯定会遇到许多的问题,比如在第三章学习的代数系统中的半群与运算,关于单位元与逆元素这两个知识点遇到一些问题。但是通过反复的理解概念及做练习题和与同学交流,最后还是解决了这些问题。当解决问题的时候心中有一种成就感。
学习离散数学的过程中,也有许多的乐趣。但在轻松学习的过程中,还得从中学到东西,学到道理。我在学习这门课程之后,对我的专业知识方面有了很大的帮助,让我的思维有了进一步的发散,使我在其他的学科中受益匪浅。
第二篇:离散数学复习总结+试题
离散数学
第一章:命题逻辑
目标语言:表达判断的一些语言的汇集。
判断:对事物有肯定或否定的一种思维模式。
命题:能表达判断语言的陈述句。
原子命题:不能分解为更简单陈述句的语句
复合命题:由联结词,标点符号和原子命题复合构成的命题,称作复合命题。
命题标识符:表示命题的符号。
命题变元:只表示命题位置标志的命题标识符。
原子变元:当命题变元表示原子命题的时候。
否定:
合式公式:命题推演的合式公式规定为:
(1) 单个命题边缘本省是一个合式公式。
(2) 如果A是合式公式,那么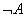 是合式公式
是合式公式
(3) 如果A和B都是合式公式,那么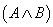 ,
, ,
,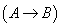 和
和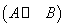 都是合式公式。?
都是合式公式。?
(4) 当且仅当能够有限次地应用(1)、(2)、(3)所得到的包含命题的变元,联结词和括号的符号串是合式公式。
翻译:把自然语言中有些语句翻译成数理逻辑中的形式符号。
优先次序:联结词运算的优先次序为: 。
。
真值表:在命题公式中,根据分量指派真值的各种可能组合,旧确定了这个命题公式的各种真值情况,把它们汇列成表,就是命题的真值表。
逻辑相等:给定两个命题公式 和
和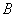 ,设
,设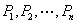 为任一组真值指派,
为任一组真值指派, 和
和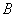 的真值都相同,则称
的真值都相同,则称 和
和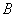 是等价的或逻辑相等,记作:
是等价的或逻辑相等,记作: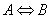
子公式:如果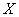 是合式公式
是合式公式 的一部分,且
的一部分,且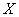 本身也是一个合式公式,则称
本身也是一个合式公式,则称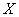 为公式
为公式 的子公式。
的子公式。
定理:设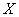 是合式公式
是合式公式 的子公式,若
的子公式,若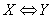 ,则将
,则将 中的
中的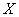 用
用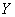 来置换,所得公式B与公式A等价,即
来置换,所得公式B与公式A等价,即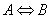 。
。
重言式:给定一个命题公式,若无论对分量进行怎样的指派,其对应的真值永为真,则称命题公式为重言式或永真公式。
矛盾式:给定一个命题公式,若无论对分量进行怎样的指派,其对应的真值永为假,则称命题公式为矛盾式或永假公式。
蕴涵式:当且仅当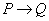 是一个重言式时,称
是一个重言式时,称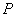 蕴涵
蕴涵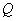 ,并记作
,并记作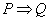 。
。
逆转式:对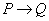 来说,
来说,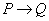 称为其逆转式。
称为其逆转式。
反换式:对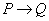 来说,
来说,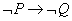 称为其反换式。
称为其反换式。
逆反式:对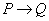 来说,
来说, 称为其逆反式。
称为其逆反式。
定理:任何两个重言式的合取或析取时一个重言式。
定理:一个重言式,对同一分量都用任何合取公式置换,其结果仍为一重言式。
定理:设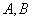 是两个命题公式,
是两个命题公式,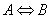 当且仅当
当且仅当 为一个重言式。
为一个重言式。
定理:设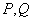 是两个命题公式,
是两个命题公式,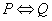 的充要条件是
的充要条件是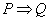 ,且
,且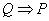
最小联结词组:对于任何一个命题公式,都能由仅含这些连接词的命题公式等价代换,而比这些联结词再少的命题公式不能对给定的公式作等价代换,这样的连接词组就是最小联结词。
对偶式:在给定的命题公式 中,使联结词
中,使联结词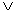 变为
变为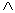
第二章:谓词公式
谓词:在反应判断的句子中,用以刻画客体的性质或关系。
谓词填式:把谓词字母后填以客体所得的式子称为谓词填式。
n元谓词: 由n个客体插入到固定位置上的谓词填式称为n元谓词。
命题函数:由一个谓词,一些客体变元组成的表达式称为简单命题函数。命题函数不是一个命题,只有当客体变元取特定一个名称时才成为命题。
复合命题函数:由一个或n个简单命题函数以及括号、逻辑连接词组成的表达式成为复合命题函数。
个体域:在命题函数中,命题变元的论述称为个体域。
全总个体域:把各种个体域综合在一起,作为论述范围的域,成为全总个体域。
全称量词:符号“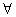 ”称为全称量词,表示“对于所有的”,“每一个”,“至少有一个”,“对任意一个”,“凡”,“一切”等词。
”称为全称量词,表示“对于所有的”,“每一个”,“至少有一个”,“对任意一个”,“凡”,“一切”等词。
存在量词:符号“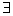 ”称为存在量词,用以表达“某个”,“存在一些”,“至少有一个”,“对于一些”等词。
”称为存在量词,用以表达“某个”,“存在一些”,“至少有一个”,“对于一些”等词。
存在唯一量词:符号“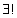 ”称为存在唯一量词,用以表达“恰有一个”,“存在唯一一个”等词。
”称为存在唯一量词,用以表达“恰有一个”,“存在唯一一个”等词。
特性谓词:使用全总个体域,限定客体变元变化范围的量词,称为特性谓词。
原子公式:把形如 称为谓词演算的原子公式,其中,
称为谓词演算的原子公式,其中,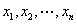 是客体变元。
是客体变元。
合式公式:谓词演算的合式公式由如下各条组成:
(1) 原子谓词公式是合式公式
(2) 若 是合式公式,则
是合式公式,则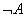 是一个合适公式
是一个合适公式
(3) 若 和
和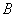 都是合适公式,则
都是合适公式,则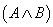 ,
, ,
,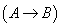 和
和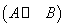 是合适公式
是合适公式
(4) 如果 是合适公式,
是合适公式,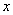 是中出现的任何变元,则
是中出现的任何变元,则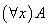 ,
,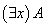 和
和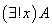 都是合式公式。
都是合式公式。
(5) 只有经过有限次的应用(1)、(2)、(3)、(4)所得到的公式才是合式公式。
指导变元:给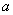 定为一个谓词公式,其中有一部分公式形式为
定为一个谓词公式,其中有一部分公式形式为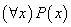 ,或
,或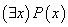 ,或
,或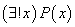 。这里
。这里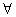 ,
,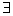 ,
,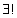 的后面跟
的后面跟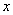 的称为相应量词的指导变元
的称为相应量词的指导变元
辖域:给定谓词公式中,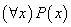 ,
,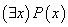 和
和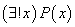 中的
中的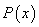 称为相应量词的辖域。
称为相应量词的辖域。
约束变元:在作用域中,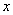 的一切出现,称为
的一切出现,称为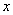 在公式
在公式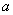 中的约束出现,所有约束出现的变元。
中的约束出现,所有约束出现的变元。
自由变元:在谓词公式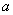 中,除去约束变元以外所出现的变元。
中,除去约束变元以外所出现的变元。
换名:对公式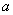 中的约束变元,遵照一定的规则跟该名称符号。
中的约束变元,遵照一定的规则跟该名称符号。
代入:是对自由变元代以式子,代入后的结果式是原式的特例。
赋值:在谓词公式中常包含命令变元和课题变元,当客体变元由确定的课题所取代,命题变元用确定的命题所取代时,就称为对谓词公式赋值。一个谓词公式经过赋值以后,就称为具有确定真值的命题。
等价:给定任何两个谓词公式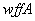 和
和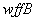 ,设它们有共同的个体域
,设它们有共同的个体域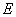 ,若对
,若对 和
和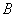 的任一组变元进行赋值所得命题的真值相同,则称谓词公式
的任一组变元进行赋值所得命题的真值相同,则称谓词公式 和
和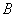 在
在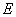 上是等价的,并记为
上是等价的,并记为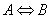 。
。
有效:给定任意谓词公式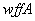 ,对于其个体域
,对于其个体域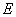 ,对于
,对于 的所有赋值,
的所有赋值,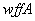 为真,则称
为真,则称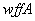 在
在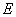 上是有效的(或永真的)。
上是有效的(或永真的)。
不可满足的:一个谓词公式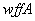 ,如果在所有赋值下都为假,则称该
,如果在所有赋值下都为假,则称该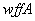 为不可满足的(或、永假的)。
为不可满足的(或、永假的)。
可满足的:一个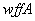 ,如果至少在一种赋值下为真,则称该
,如果至少在一种赋值下为真,则称该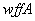 为可满足的。
为可满足的。
谓词演算中的等价公式和蕴涵公式:命题演算中的等加工时表和蕴涵公式表都可推广到谓词演算中的使用,此外还有如下一些谓词公式的等价公式和蕴涵公式。
(1) 蕴涵公式:
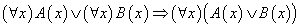

(2) 等价公式:
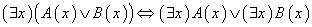 ,
,
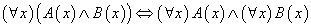 ,
,
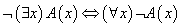 ,
,
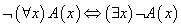 ,
,
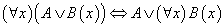 ,
,
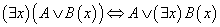 ,
,
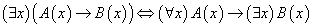 ,
,
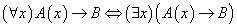 ,
,
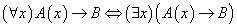 ,
,
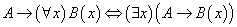 ,
,
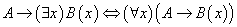 。
。
前束范式:一个公式如果量词均包含在全式的开头,它们的作用域延伸到整个公式的末尾,则该公式叫做前束范式,其形式为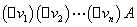 ,其中
,其中 是量词,
是量词,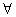 或
或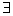 ,
,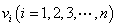 是客体变元,
是客体变元, 是没有量词的谓词公式。
是没有量词的谓词公式。
前束合取范式:一个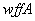 如果具有如下形式,则称为前束合取范式:
如果具有如下形式,则称为前束合取范式:
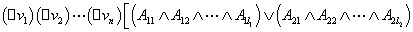
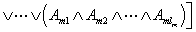
其中 是量词,
是量词,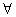 或
或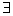 ,
,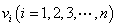 是客体变元,
是客体变元,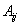 是原子公式或其否定。
是原子公式或其否定。
前束析取范式:一个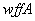 如果具有如下形式,则称为前束合取范式:
如果具有如下形式,则称为前束合取范式:
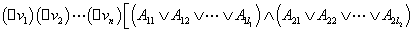

其中 是量词,
是量词,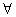 或
或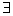 ,
,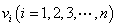 是客体变元,
是客体变元,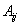 是原子公式或其否定。
是原子公式或其否定。
定理:任意一个谓词公式均和一个前束范式等价。
定理:每一个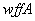 都可以转化为与其等价的前束合取范式。
都可以转化为与其等价的前束合取范式。
定理:每一个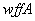 都可以转化为与其等价的前束析取范式。
都可以转化为与其等价的前束析取范式。
全称指定规则:如果对论域中所指的客体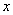 ,
,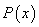 成立,则对论域中某个任意客体
成立,则对论域中某个任意客体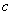 ,有
,有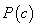 成立。这个规则可表示为
成立。这个规则可表示为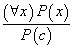 ,简称US。
,简称US。
全程推广规则:如果能够证明对论域中每一个客体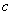 断言
断言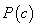 都成立,则可得到结论对论域
都成立,则可得到结论对论域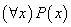 。这个规则可表示为
。这个规则可表示为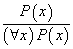 ,简称UG。
,简称UG。
存在指定规则:如果对论域中某些客体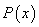 成立,则对论域中某个制定客体
成立,则对论域中某个制定客体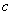 ,使得
,使得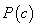 成立。这个规则可表示为
成立。这个规则可表示为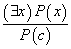 ,简称ES。
,简称ES。
存在推广规则:如果能够证明对论域中每一个客体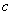 ,有
,有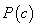 成立,则在论域中必存在
成立,则在论域中必存在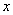 ,使得
,使得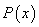 成立。这个规则可表示为
成立。这个规则可表示为 ,简称EG。
,简称EG。
带有量词蕴含公式和等价公式
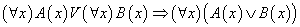
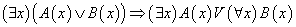
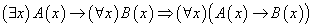
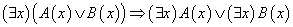
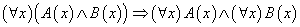
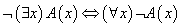
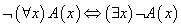
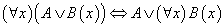
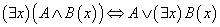
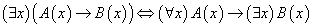

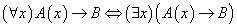
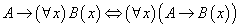
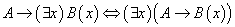
图论:
图:三元有序组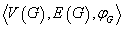 称为图,其中
称为图,其中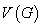 是非空结点集,
是非空结点集,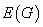 是连接结点的边集,
是连接结点的边集,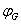 是边集到节点无序偶(有序偶)集合上的函数。因每条边总是关联连个节点,故图常记为
是边集到节点无序偶(有序偶)集合上的函数。因每条边总是关联连个节点,故图常记为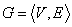 。
。
无向边:边是两个点的无序偶对。
有向边:边是两个点的序偶。
有向图:每一条边都是有向边的图。
无向图:每一条边都是无向边的图。
混合图:图既有有向边又有无向边的图。在此暂不讨论。
邻接点:若两个点有边(有向或无向)相连,则称这两个点邻接。
邻接边:若两条边有公共点,则称这两条边邻接。
环:只与一个结点关联的边(可以作为有向边,也可以作为无向边)
结点的度:与结点v关联的边数(约定:对于环,度加2)。记为deg(v)
图 的最大度:
的最大度: 。
。
图 的最小度:
的最小度: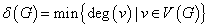
出度:在有向图中,由一个结点射出的边数称为该结点的出度。
入度:在有向图中,射入一个结点的边数称为该结点的入度。
定理1: 每个无向图,结点度数的总和等于边数的两倍。即: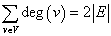
定理2:在任何图中,度数为奇数的结点个数必定是偶数。
定理3:在有向图中,所有结点的入度之和等于所有结点的出度之和。
关联:边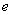 连接了点
连接了点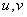 ,则称点
,则称点 和边
和边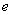 关联,或称边
关联,或称边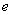 和点
和点 关联
关联
注意:邻接是指点点或边边的关系,关联是指点边的关系
孤立点:在图中不与任何其他结点邻接的点。
零图:仅由孤立点组成的图(可以有多个结点),即E是空集。
平凡图:只有一个孤立点组成的图,即只有一个结点的零图。
图是序偶,序偶元素是集合,第二个集合是第一个集合的元素的偶对的集合。
注意:1)图不同于图解,图解是在平面上用点、边表示点的集合及其点点之间的关系。
2)对于同一个图,可以画出不同形状的图解,但这些图解的一定是同构的。
3)对于同一个图解,可以写出用不同符号表示的图(G = < V, E >的形式),但这些图也是彼此同构的
平行边:连接于同一对结点间的多条边。
多重图:含有平行边的图。
简单图:不含有平行边的图。以后只讨论简单图。
完全图:每一对结点见都有边相连的简单图。有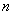 个结点的完全图记为
个结点的完全图记为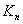 。
。
定理4: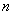 个结点的无向完全图
个结点的无向完全图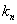 的边数为
的边数为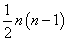 。
。
相对与完全图的补图:由图 中所有节点以及所有能使
中所有节点以及所有能使 成为完全图的添加边组成图,称为
成为完全图的添加边组成图,称为 相对于完全图的补图,简称
相对于完全图的补图,简称 的补图,记作
的补图,记作 。换句话说,是完全图去掉G的边形成的图。
。换句话说,是完全图去掉G的边形成的图。
子图:点的子集,以及相应的边的子集,叫原图的子图。
生成子图:如果 的子图包含的所有结点,称该子图为
的子图包含的所有结点,称该子图为 的生成子图。
的生成子图。
相对于图 的补图:设
的补图:设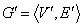 是图
是图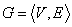 的子图,若有图
的子图,若有图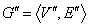 使
使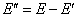 ,且
,且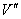 中仅包含
中仅包含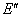 的边所关联的结点,则
的边所关联的结点,则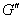 是子图
是子图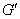 `相对于图
`相对于图 的补图。
的补图。
图的同构:设图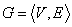 及
及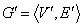 ,如果存在一一对应的映射
,如果存在一一对应的映射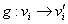 ,且
,且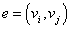 或
或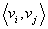 是
是 的一条边,当且仅当
的一条边,当且仅当 或
或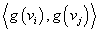 是
是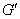 的一条边,则
的一条边,则 同
同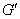 同构,记为
同构,记为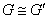
两图的同构的判断方法:
1)结点数、边数要相同。
2)度数相同的结点数目相等。
3)有相同的特性:
a. 都有长度为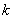 的回路。
的回路。
b. 度为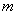 的点正好和度为
的点正好和度为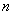 的点有边相连
的点有边相连
c. 有环的点(或其他特征)与最大度数的点的距离相同。
注意:同构的图本质上是同一个图,只不过结点的编号不同而已。
因此,对于同一个图,可以画出不同形状的图解,但这些图解的一定是同构的。对于同一个图解,可以对结点进行不同的编号,得到不同的图的表示,这些图同构。
路:设 是关联于结点
是关联于结点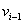 和
和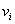 的边,交替序列
的边,交替序列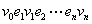 称为连接
称为连接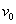 到
到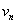 的路。
的路。
回路:在交替序列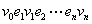 中,当
中,当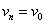 时称此交替序列为回路
时称此交替序列为回路
迹:所有边均不相同的一条路。
圈:在通路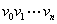 中,
中,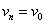 。即:闭的通路;
。即:闭的通路;
通路:所有结点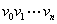 均不相同的一条路。
均不相同的一条路。
连通:在无向图 中,结点
中,结点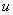 和
和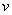 之间若存在一条路,则称结点
之间若存在一条路,则称结点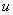 和结点
和结点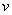 两点连通;
两点连通;
连通分支:结点之间的连通性是结点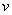 上的等价关系,由该等价关系可将
上的等价关系,由该等价关系可将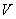 分成非空子集
分成非空子集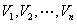 ,每一个非空子集
,每一个非空子集 确定了一个连通子图记为
确定了一个连通子图记为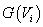 。
。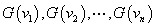 称为图
称为图 的连通分支。图
的连通分支。图 的连通分支数记为
的连通分支数记为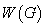 。
。
连通图:无向图 只有一个连通分支。换句话说,任意两点都连通的无向图叫连通图。
只有一个连通分支。换句话说,任意两点都连通的无向图叫连通图。
点割集:设无向图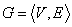 为连通图,若有点集
为连通图,若有点集 ,使图
,使图 删除了
删除了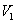 中的所有结点后所得子图是不连通的,而删除了
中的所有结点后所得子图是不连通的,而删除了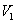 的任何真子集后,所得的子图仍是连通图,则称
的任何真子集后,所得的子图仍是连通图,则称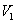 是
是 的一个点割集。
的一个点割集。
割点:点割集只有一个点;换句话说,连通图G去掉该点后,变得不连通了;
点连通度:在图 中为了产生一个不连通图需要删去的点的最少数目称为点连通度,记为
中为了产生一个不连通图需要删去的点的最少数目称为点连通度,记为
 。若
。若 不连通,
不连通,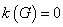 ;若
;若 有割点,
有割点, 。
。
边割集:设无向图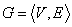 为连通图,若有边集
为连通图,若有边集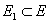 ,使图
,使图 删除了
删除了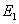 中的所有边后所得子图是不连通的,而删除了
中的所有边后所得子图是不连通的,而删除了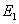 的任何真子集后,所得的子图仍是连通图,则称
的任何真子集后,所得的子图仍是连通图,则称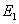 是
是 的一个边割集。
的一个边割集。
割边:由一条边构成的边割集,称该边为割边(或桥)。换句话说,G去掉该边后,变得不连通了;
边连通度:了产生一个不连通图需要删去的边的最少数目称为边连通度,记为
 。若G不连通,
。若G不连通,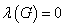 。
。
可达:在有向图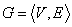 中从结点
中从结点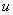 到
到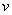 有一条路,称从
有一条路,称从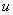 到
到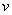 可达。
可达。
单侧连通:在简单有向图 中,任何一对结点间,至少从一个结点到另一个结点是可达的。
中,任何一对结点间,至少从一个结点到另一个结点是可达的。
强连通:在简单有向图 中,任何一对结点的两者之间相互可达。
中,任何一对结点的两者之间相互可达。
弱连通:在简单有向图 中,略去边的方向,将它看成无向图后,图是连通的。
中,略去边的方向,将它看成无向图后,图是连通的。
强分图:在简单有向图中,具有强连通性质的最大子图。
弱分图:在简单有向图中,具有弱连通性质的最大子图。
单侧分图:在简单有向图中,具有单侧连通连通性质的最大子图。
定理5:在一个具有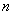 个结点的图中,如果从结点
个结点的图中,如果从结点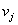 到结点
到结点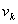 存在一条路,则从结点
存在一条路,则从结点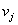 到结点
到结点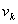 必存在一条不多于
必存在一条不多于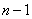 条边的路。
条边的路。
定理6:对于任何一个图 ,有
,有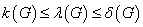 。
。
定理7:一个连通无向图中的结点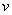 为割点的充分必要条件是存在两个结点
为割点的充分必要条件是存在两个结点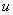 和
和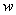 ,使结点
,使结点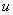 和
和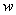 的每一条路都是通过
的每一条路都是通过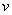 。
。
定理8:一个有向图是强连通的,当且仅当 中有一个回路,它至少包含每个结点一次。
中有一个回路,它至少包含每个结点一次。
定理9:在有向图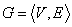 中,它的每一个结点位于且只位于一个强分图中。
中,它的每一个结点位于且只位于一个强分图中。
3. 图的表示方法:
邻接距阵:设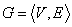 是一个有
是一个有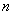 个结点的简单图,即
个结点的简单图,即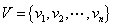 ,
,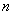 阶方阵
阶方阵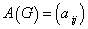 ,其中
,其中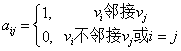 ,称
,称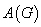 为图
为图 的邻接距阵。
的邻接距阵。
可达性距阵:令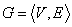 是一个简单有向图,假定
是一个简单有向图,假定 的结点已编好序,即
的结点已编好序,即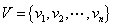 ,则
,则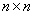 距阵
距阵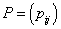 ,其中
,其中 ,称
,称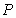 是图
是图 的可达性距阵。
的可达性距阵。
完全关联距阵:给定无向图 ,令
,令 和
和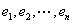 分别是
分别是 的结点和边,则距阵
的结点和边,则距阵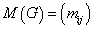 ,其中
,其中 ,则称
,则称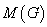 为无向图
为无向图 的完全关联距阵。
的完全关联距阵。
若给定有向图 ,则距阵
,则距阵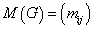 ,其中
,其中 ,则称
,则称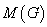 为无向图
为无向图 的完全关联距阵。
的完全关联距阵。
定理10:设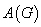 是图
是图 的邻接距阵,则
的邻接距阵,则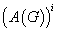 中的
中的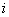 行
行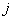 列元素
列元素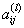 等于
等于 中连接
中连接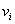 与
与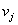 的长度为
的长度为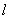 的路的数目。
的路的数目。
定理11:如果连通图 有
有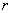 个结点,则其完全关联距阵
个结点,则其完全关联距阵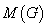 的秩为
的秩为 ,即
,即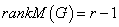 。
。
欧拉路(回路):在无孤立结点的图 中,存在一条路(回路),经过图
中,存在一条路(回路),经过图 中每条边一次且仅一次。
中每条边一次且仅一次。
单向欧拉路(回路):给定有向图 中,存在通过图
中,存在通过图 中每条边一次且仅一次的一条单向路(回路)。
中每条边一次且仅一次的一条单向路(回路)。
汉密尔顿路(回路):给定图 ,存在一条路(回路)经过图中每个结点一次且仅一次。
,存在一条路(回路)经过图中每个结点一次且仅一次。
判断哈密顿图的充分条件:
1)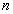 个结点的简单图,如果
个结点的简单图,如果 中每一对结点度数之和大于等于
中每一对结点度数之和大于等于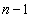 ,则图中存在一条哈密顿路;(证明比较复杂,思路是:不断地加长已找到的路,直到这条路包含了所有结点,由于有了上述条件,故可以通过破圈的方法延长路,为此,要先证明满足该条件的图一定是连通图)
,则图中存在一条哈密顿路;(证明比较复杂,思路是:不断地加长已找到的路,直到这条路包含了所有结点,由于有了上述条件,故可以通过破圈的方法延长路,为此,要先证明满足该条件的图一定是连通图)
2)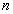 个结点的简单图,如果
个结点的简单图,如果 每一对结点度数之和大于等于
每一对结点度数之和大于等于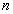 ,则图中存在一条哈密顿回路;
,则图中存在一条哈密顿回路;
图 的闭包:给定图
的闭包:给定图 有
有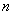 个结点,若将图
个结点,若将图 中度数之和至少是
中度数之和至少是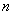 的非邻接点连接起来得图
的非邻接点连接起来得图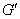 ,对图
,对图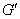 重复上述步骤,直到不再有这样的结点对存在为止,此时得到的图称为原图
重复上述步骤,直到不再有这样的结点对存在为止,此时得到的图称为原图 的闭包,记作
的闭包,记作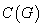 。
。
欧拉图:具有欧拉回路的图。
汉密尔顿图:具有汉密尔顿回路的图。
定理12:无向图 具有一条欧拉路,当且仅当是连通的,且有零个或两个奇数度结点。
具有一条欧拉路,当且仅当是连通的,且有零个或两个奇数度结点。
推论:  是欧拉图当且仅当
是欧拉图当且仅当 连通且均为偶数度结点。
连通且均为偶数度结点。
定理13:有向图 具有一条单向欧拉回路,当且仅当是连通的,且每个结点入度等于出度。有向图
具有一条单向欧拉回路,当且仅当是连通的,且每个结点入度等于出度。有向图 具有单向欧拉路,当且仅当是连通的,且有两个结点,其中一个结点的入度比出度大1,另一个结点的入度比出度小1,其他结点的出度等于入度。
具有单向欧拉路,当且仅当是连通的,且有两个结点,其中一个结点的入度比出度大1,另一个结点的入度比出度小1,其他结点的出度等于入度。
定理14:若图 具有汉密顿回路,则对于结点集的每个非空子集,均有
具有汉密顿回路,则对于结点集的每个非空子集,均有 成立,其中
成立,其中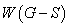 是
是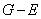 中的连通分支数。
中的连通分支数。
定理15: 设 是具有
是具有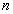 个结点的简单图,如果
个结点的简单图,如果 中每一对结点度数之和大于等于
中每一对结点度数之和大于等于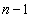 ,则在
,则在 中存在一条汉密尔顿路。
中存在一条汉密尔顿路。
定理16:设 是具有
是具有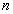 个结点的简单图,如果
个结点的简单图,如果 中每一对结点度数之和大于等于
中每一对结点度数之和大于等于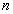 ,则在
,则在 中存在一条汉密尔顿回路。
中存在一条汉密尔顿回路。
定理17:当且仅当一个简单图的闭包是汉密尔顿图时,这个简单图是汉密尔顿图。
可嵌入平面 一个图 ,如果能把
,如果能把 的所有结点和边画在平面上,且使得任何两条边除了端点外没有其他的交点,则称
的所有结点和边画在平面上,且使得任何两条边除了端点外没有其他的交点,则称 是可嵌入平面,或简称
是可嵌入平面,或简称 是平面图。
是平面图。
面 设 是一连通平面图,由图中的边所包围的区域,在区域内既不包含图的结点,也不包含图的边,这样的区域称为
是一连通平面图,由图中的边所包围的区域,在区域内既不包含图的结点,也不包含图的边,这样的区域称为 的一个面。(一个面的边界的回路长度称为该面的次数。)
的一个面。(一个面的边界的回路长度称为该面的次数。)
2度结点内同构 给定两图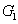 和
和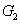 ,如果它们是同构的,或者通过反复插入或除去度数为2的结点后,使
,如果它们是同构的,或者通过反复插入或除去度数为2的结点后,使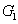 与
与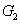 同构,则称该图是2度结点内同构。
同构,则称该图是2度结点内同构。
定理18 一个有限平面图,面的次数之和等于其边数的两倍。
定理19 设连通的平面图 ,共有个
,共有个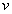 结点,
结点,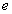 条边和
条边和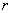 个面,则欧拉公式
个面,则欧拉公式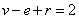 成立。
成立。
定理20 设 是一个有个结点和条边的连通简单平面图,若
是一个有个结点和条边的连通简单平面图,若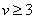 ,则
,则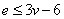 。
。
定理21 一个图是平面图当且仅当它不包含与 或
或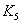 在2 度结点内同构的子图。
在2 度结点内同构的子图。
判断平面图的方法:
1. 证明不满足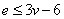
2. 包含了库拉托夫斯基图子图
3. 证明经边收缩,变成库拉托夫斯基图;
对偶图::给定平面图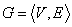 ,它具有面
,它具有面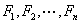 。若有图
。若有图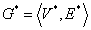 满足下述条件:则称图
满足下述条件:则称图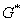 是图
是图 的对偶图。
的对偶图。
a)对于图 的任一个面
的任一个面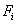 ,内部有且仅有一个结点
,内部有且仅有一个结点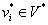 。
。
b)对于图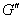 的面
的面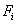 ,
,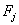 的公共边界
的公共边界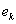 ,存在且仅存在一条边
,存在且仅存在一条边 ,使
,使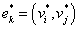 ,且与
,且与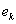 相交。
相交。
c)当且仅当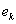 只是一个面
只是一个面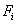 的边界时,存在一个关联于
的边界时,存在一个关联于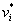 的环
的环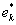 与
与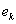 相交。
相交。
自对偶图:如果图 的对偶图
的对偶图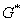 同构于
同构于 ,称
,称 是自对偶图。
是自对偶图。
正常着色:图 的每一个结点指定一种颜色,使得没有两个邻接的点有同一种颜色。
的每一个结点指定一种颜色,使得没有两个邻接的点有同一种颜色。
着色数:对于图 着色时,需要的最少颜色数称为
着色时,需要的最少颜色数称为 的着色数,记作
的着色数,记作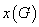 。
。
定理22:对于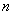 个结点的完全图
个结点的完全图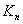 ,有
,有 。
。
定理23:设 为一个至少具有三个结点的简单连通平面图,则
为一个至少具有三个结点的简单连通平面图,则 中必有一结点
中必有一结点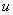 ,使
,使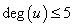 。
。
定理24:任意平面图 最多是五色的。
最多是五色的。
树:一个连通无回路的无向图。
树叶:树中度数为1的节点。
内点:度数大于1的节点称内点或分支点。
森林:一个无回路的无向图称为森林,它的每一个连通分图是树。
生成树:如果图 的生成子图是一棵树,该树称为图G的生成树。记为
的生成子图是一棵树,该树称为图G的生成树。记为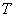
树枝:图 的一颗生成树
的一颗生成树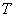 ,树
,树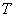 的边称作树枝。
的边称作树枝。
弦:图 的不在生成树
的不在生成树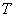 的边称作弦,所有弦的集合称为生成树
的边称作弦,所有弦的集合称为生成树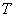 的补。
的补。
树权:带权树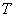 中所有边权之和称为树权。
中所有边权之和称为树权。
最小生成树:图 的所有生成树中,树权最小的生成树。
的所有生成树中,树权最小的生成树。
定理25:给定图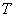 ,以下关于图的定义是等价的:
,以下关于图的定义是等价的:
1) 连通无回路。
2) 无回路且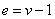 ,其中
,其中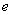 是边数,
是边数,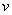 是节点数。
是节点数。
3) 连通且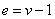 。
。
4) 无回路,但增加一条新边,得到一个且仅有一个回路。
5) 连通但删去任一边后便不连通。
6) 每一对节点之间有且仅有一条路。
定理26:任一树至少有两片树叶。
定理27:连通图至少有一颗生成树。
定理28:一条回路和任何一颗生成树的补至少有一条公共边。
定理29:一个边割集和任何生成树至少有一条公共边。
定理30:在图G中有n个节点,其最小生成树算法如下:
a) 选取最小边权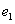 ,置边数
,置边数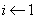 ;
;
b) 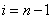 结束,否则转c);
结束,否则转c);
c) 设已选择边为,在 中选取不同于
中选取不同于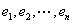 的边
的边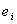 ,使
,使 中无回路且是满足此条件的最小边。
中无回路且是满足此条件的最小边。
d) 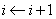 ,转b)。
,转b)。
定理31:设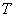 是连通图
是连通图 的生成树,令
的生成树,令 ,但
,但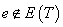 ,则
,则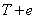 包含
包含 中唯一的一个圈。
中唯一的一个圈。
有向树:如果一个有向图在不考虑边的方向时是一棵树,则称该有向图为有向树。
根树:一颗有向树如果恰有一个节点的入度为0,其余所有节点的入度都为1,则称它为根树。
根:入度为0的结点。
叶:出度为0的结点。
有序树:根树中结点或边的次序被指定,称此根树为有序树。
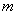 杈树 :每一结点的出度小于或等于
杈树 :每一结点的出度小于或等于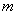 的根树。
的根树。
完全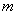 杈树:每一结点的出度恰好等于
杈树:每一结点的出度恰好等于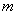 或0的根树。
或0的根树。
正则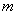 杈树 :在完全
杈树 :在完全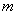 杈树中,所有树叶层次相同。
杈树中,所有树叶层次相同。
通路长度:在根树中,从树根到某结点的通路中的边数称为此结点的长度。
内部通路长度:分支点的通路长度。
外部通路长度:树叶的通路长度。
二杈树的权:一颗二杈树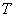 ,如果每一片树叶都带权,带权为
,如果每一片树叶都带权,带权为 的树叶,其通路长度为
的树叶,其通路长度为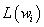 ,
,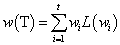 称为带权二杈树的权。
称为带权二杈树的权。
最优树:在所有带权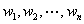 的二杈树中,
的二杈树中,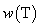 最小的那棵树,称为最优树。
最小的那棵树,称为最优树。
前缀码:给定一个序列的集合,若没有一个序列是另一个序列的前缀,该序列记和称为前缀码。
定理32:设有完全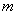 叉树,其树叶树为
叉树,其树叶树为 ,分支点数为
,分支点数为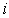 ,则
,则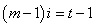
定理33:若完全二叉树有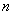 个分支点,且内部通路长度的总和为
个分支点,且内部通路长度的总和为 ,外部通路长度的总和为
,外部通路长度的总和为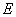 ,则
,则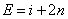
定理34:设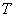 为带权
为带权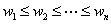 的最优树,则
的最优树,则
a) 带权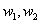 的树叶
的树叶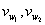 是兄弟;
是兄弟;
b) 以树叶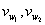 为儿子的分支点,其通路长度最长。
为儿子的分支点,其通路长度最长。
定理35:设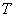 为带权
为带权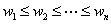 的最优树,若将带权
的最优树,若将带权 和
和 的树叶为儿子的分支点改为
的树叶为儿子的分支点改为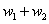 带权的树叶,得到一颗新树
带权的树叶,得到一颗新树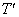 ,则
,则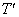 也是最优树。
也是最优树。
定理36:任何一颗二叉树的树叶可对应一个前缀码。
定理37:任何一个前缀码都对应一颗二叉树。
有关图论的证明题:
集合论、数理逻辑的大多数证明题大多数要按某些固定的“框架”来叙述,严格套用相应的定义的每个条件,例如证明某个关系是等价关系、证明某个代数系统是群等。而图论的证明则没有规律可循,用归纳法、抽屉原理、代数演算法、分类说明法等等,视问题的内容而定,总之,要说清楚,特别是很直观的问题,更应描述得简洁清晰,如P272、P280定理的证明;有时,甚至一、两句话就可以证明完毕;有时,则要分几步,先证明一些后面要用得到的结果,如哈密顿定理的证明;因此,要做好图论的证明题,必须:熟悉相关的定理,以及这些定理的证明方法(通过证明过程理解定理),有时需用另类思路,如8*8个小格子去掉对角两个小格子后,不能被31个1*2的长方块所覆盖。
思考:连通关系是等价关系吗?
无向图是否具有欧拉通路或回路的判定:
 有欧拉通路
有欧拉通路 连通,
连通, 中只有两个奇度顶点(它们分别是欧拉通路的两个端点)。
中只有两个奇度顶点(它们分别是欧拉通路的两个端点)。
 有欧拉回路(
有欧拉回路( 为欧拉图)
为欧拉图)  连通,
连通, 中均为偶度顶点。
中均为偶度顶点。
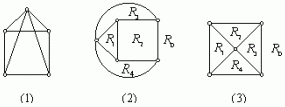
例1、以下图形能否一笔画成?

解:(1)有4个奇度顶点,无欧拉回路或通路,不能一笔画成。
(2)与(3)都是2个奇度顶点,其余均为偶度顶点,具有欧拉通路,可一笔画成。
(4)图中均为偶度顶点,具有欧拉回路,可一笔画成。
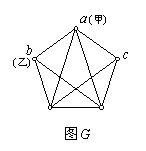 例2、“两只蚂蚁比赛问题”。两只蚂蚁甲、乙分别处在图
例2、“两只蚂蚁比赛问题”。两只蚂蚁甲、乙分别处在图 中的顶点
中的顶点 处,并设图中各边长度相等。甲提出同乙比赛:从它们所在顶点出发,走过图中所有边最后到达顶点
处,并设图中各边长度相等。甲提出同乙比赛:从它们所在顶点出发,走过图中所有边最后到达顶点 处。如果它们速度相同,问谁最先到达目的地?
处。如果它们速度相同,问谁最先到达目的地?
解:图 中,有两个奇度顶点
中,有两个奇度顶点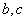 ,因此存在从
,因此存在从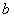 到
到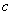 的欧拉通路,蚂蚁乙走到
的欧拉通路,蚂蚁乙走到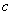 只要走一条欧拉通路,边数为9,而蚂蚁甲要想走完图中所有边到达
只要走一条欧拉通路,边数为9,而蚂蚁甲要想走完图中所有边到达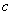 ,至少要先走一条边到达
,至少要先走一条边到达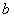 ,再走一条欧拉通路,故它至少要走10条边到达
,再走一条欧拉通路,故它至少要走10条边到达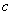 ,所以乙必胜。
,所以乙必胜。
有向图是否具有欧拉通路或回路的判定:
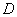 有欧拉通路
有欧拉通路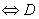 连通,除两个顶点外,其余顶点的入度均等于出度,这两个特殊的顶点中,一个顶点的入度比出度大1,另一个顶点的入度比出度小1。
连通,除两个顶点外,其余顶点的入度均等于出度,这两个特殊的顶点中,一个顶点的入度比出度大1,另一个顶点的入度比出度小1。

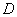 有欧拉回路(
有欧拉回路(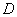 为欧拉图)
为欧拉图) 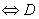 连通,
连通,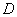 中所有顶点的入度等于出度。
中所有顶点的入度等于出度。
例3、判断以下有向图是否欧拉图。
解:(1)不是欧拉图,也无欧拉通路,(2)不是欧拉图,但有欧拉通路,(3)是欧拉图。
判定哈密尔顿回路和通路:
 遗憾的是至今尚未找到一个判别哈密尔顿回路和通路的充分必要条件。虽然有些充分非必要,或必要非充分条件,但在大部分情况下,还是采用尝试的办法。
遗憾的是至今尚未找到一个判别哈密尔顿回路和通路的充分必要条件。虽然有些充分非必要,或必要非充分条件,但在大部分情况下,还是采用尝试的办法。
例1、判断下图是否具有哈密尔顿回路,通路。
解:(1) 存在哈密尔顿通路,但不存在哈密尔顿回路。(2) 是哈密尔顿图,存在哈密尔顿回路和通路。(3) 不存在哈密尔顿回路,也不存在哈密尔顿通路。
 例2、画一个无向图,使它
例2、画一个无向图,使它
(1) 具有欧拉回路和哈密尔顿回路,
(2) 具有欧拉回路而没有哈密尔顿回路,
(3) 具有哈密尔顿回路而没有欧拉回路,
(4) 既没有欧拉回路,也没有哈密尔顿回路。
解:所要的图分别如右:
平面图
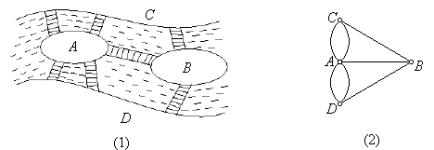
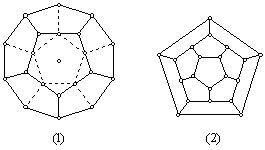
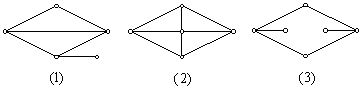
例1、判断以下图形是不是平面图:
 以上图中,(1)即
以上图中,(1)即 图,(2)是(1)的平面嵌入,故(1)是平面图。
图,(2)是(1)的平面嵌入,故(1)是平面图。
(4)是(3)的平面嵌入,故(3)是平面图。
(5)即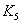 图,无论怎样画,都不可能将交叉的边全去掉,(6)是(5)的一种画法。同样,(7)即
图,无论怎样画,都不可能将交叉的边全去掉,(6)是(5)的一种画法。同样,(7)即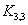 图,无论怎样画,也不可能将交叉的边全去掉,(8)是(7)的一种画法。故
图,无论怎样画,也不可能将交叉的边全去掉,(8)是(7)的一种画法。故 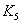 和
和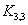 都不是平面图。
都不是平面图。
例2、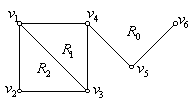 如右图所示的连通平面图,共有 3个面
如右图所示的连通平面图,共有 3个面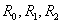 ,其中
,其中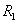 的边界
的边界 ,
,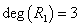 ,
, 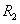 的边界
的边界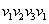 ,
,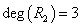 ,
,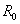 的边界为复杂回路
的边界为复杂回路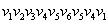 ,
,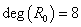 。
。
注意:(1) 一个平面图的无限面只有一个。
(2) 同一个平面图可以有不同形状的平面嵌入 (互相同构)。
 (3) 不同的平面嵌入可能将某个有限面变成无限面,而将无限面变成有限面。
(3) 不同的平面嵌入可能将某个有限面变成无限面,而将无限面变成有限面。
例3、 图(2),(3)都是图(1)的平面嵌入,图(2)中, ,图(3)中,
,图(3)中,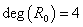 ,它们虽然形状不同,但都与(1)同构
,它们虽然形状不同,但都与(1)同构
