数学物理方程小结
第七章 数学物理定解问题
数学物理定解问题包含两个部分:数学物理方程(即泛定方程)和定解条件。
§7.1数学物理方程的导出
一般方法: 第一确定所要研究的物理量u ,第二 分析体系中的任意一个小的部分与邻近部分的相互作用,根据物理规律, 抓住主要矛盾, 忽略次要矛盾。(在数学上为忽略高级小量.)第三 然后再把物理量u随时间,空间的变为通过数学算式表示出来, 此表示式即为数学物理方程。
(一)三类典型的数学物理方程
(1)波动方程: 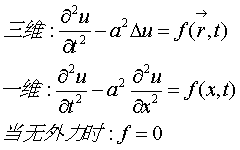
此方程 适用于各类波动问题。(特别是微小振动情况.)
(2)输运方程: 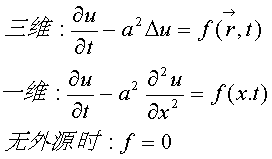
此方程 适用于热传导问题、扩散问题。
(3)Laplace 方程: 
稳定的温度和浓度分布适用的数学物理方程为Laplace 方程, 静电势u在电荷密度为零处也满足Laplace 方程 。
§7.2定解条件
定解条件包含初始条件与边界条件。
(1) 初始条件的个数等于方程中对时间最高次导数的次数。例如波动方程应有二个初始条件, 一般选初始位移u(x,o)和初始速度ut(x,0)。而输运方程只有一个初始条件选为初始分布u(x,o),而Laplace 方程没有初始条件。
…… …… 余下全文





 等.
等.

 。
。 则方程变为:
则方程变为: ,
, (8’)由边值条件可得:
(8’)由边值条件可得:
 。
。
 。
。 为常数
为常数 代于方程得:
代于方程得: ,
, (8’)
(8’) ,
,


 ,
,

 具有狄利克雷边界条件的初边值问题解的唯一性与稳定性. (15分)
具有狄利克雷边界条件的初边值问题解的唯一性与稳定性. (15分) 代入方程:
代入方程:
 都是方程的解设
都是方程的解设 代入方程得:
代入方程得: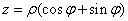 和
和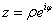
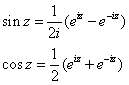
 (其中f(z)=u+iv)
(其中f(z)=u+iv) 及其领域上处处可导,则称f(z)在
及其领域上处处可导,则称f(z)在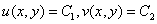 (
(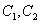 为常数)是B上的两组正交曲线族.
为常数)是B上的两组正交曲线族.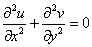
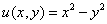 ,求虚部和这个解析函数.
,求虚部和这个解析函数.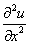 =2;
=2;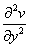 =-2;则
=-2;则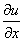 =2x;
=2x;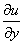 =-2y.根据C-R条件有:
=-2y.根据C-R条件有: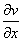 =2y;
=2y;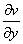 =2x.
=2x.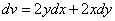 ;
;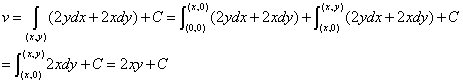 凑全微分显式法 由上式可知
凑全微分显式法 由上式可知 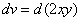
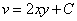
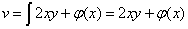 .
.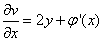 ,而由C-R条件可知
,而由C-R条件可知 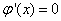 ,
,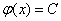 .故 v=2xy+C.
.故 v=2xy+C.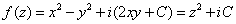
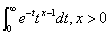 ;又称为第二类欧拉积分的为:
;又称为第二类欧拉积分的为: 。
。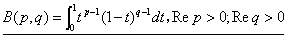 ;B函数与Г函数之间的重要关系为:
;B函数与Г函数之间的重要关系为:
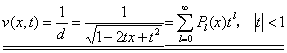 (B卷)
(B卷) ;其积分形式为:
;其积分形式为: (B卷)
(B卷)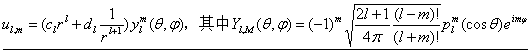
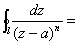

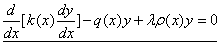
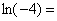
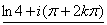
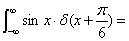
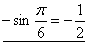
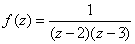 在
在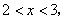 可展开为洛朗级数:
可展开为洛朗级数: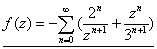
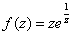 在z=0处的奇点类型为本性奇点,其留数为:
在z=0处的奇点类型为本性奇点,其留数为: 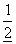 。
。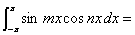 0 。
0 。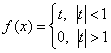 的傅里叶变换为:
的傅里叶变换为:  。
。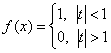 的傅里叶变换为:
的傅里叶变换为: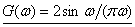 。
。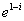 的模为
的模为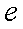 ,主辐角为: -1 。(B卷)
,主辐角为: -1 。(B卷)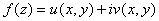 的虚部
的虚部 且
且 ,则解析函数为
,则解析函数为  。
。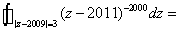 0 。
0 。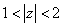 的环域上,函数
的环域上,函数 的洛朗级数展开为
的洛朗级数展开为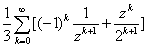
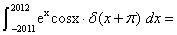
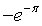 。
。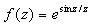 在
在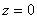 的奇点类型为 可去奇点 ,其留数为 0 。
的奇点类型为 可去奇点 ,其留数为 0 。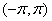 这个周期上,
这个周期上,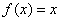 。其傅里叶级数展开为
。其傅里叶级数展开为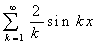
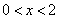 时,
时,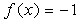 ;当
;当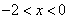 时,
时,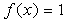 ;当
;当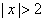 时,
时,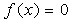 。则函数的
。则函数的 傅里叶变换为
傅里叶变换为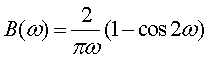
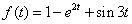 的拉普拉斯变换为
的拉普拉斯变换为 。
。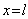 )固定的弦,用手在离弦左端长为
)固定的弦,用手在离弦左端长为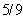 处把弦朝横向拨开距离
处把弦朝横向拨开距离 ,然后放手任其振动。横向位移
,然后放手任其振动。横向位移 的初始条件为
的初始条件为 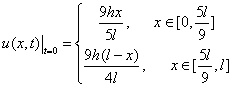 。
。 满足方程
满足方程
 为杆的密度,
为杆的密度, 为杨氏模量。
为杨氏模量。 与
与
 。现在计算这段杆在时刻
。现在计算这段杆在时刻 的相对伸长。在时刻
的相对伸长。在时刻


 ,取极限得在点
,取极限得在点
 。由虎克定律,张力
。由虎克定律,张力 等于
等于
 是在点
是在点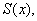 则作用在杆段
则作用在杆段 两端的力分别为
两端的力分别为

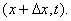







 常量,则得
常量,则得 =
=
 两点则相应的边界条件为
两点则相应的边界条件为
 为自由端,则杆在
为自由端,则杆在 |
| 等于零,因此相应的边界条件为
等于零,因此相应的边界条件为  |
| 为自由端,则相应的边界条件为
为自由端,则相应的边界条件为 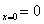
 给出,则在
给出,则在 。由虎克定律有
。由虎克定律有