数学实验报告

第二篇：Mathematica——常微分方程、拉氏变换与级数实验

§13.5                        常微分方程、拉氏变换与级数实验

[学习目标]

1.        会用Mathematica求解微分方程（组）；

2.        能用Mathematica求微分方程（组）的数值解；

3.        会利用Mathematica进行拉氏变换与逆变换；

4.        能进行幂级数和傅里叶级数的展开。

一、   常微分方程（组）

    Mathematica能求常微分方程（组）的准确解，能求解的类型大致覆盖了人工求解的范围，功能很强。但不如人灵活（例如在隐函数和隐方程的处理方面），输出的结果与教材上的答案可能在形式上不同。另外，Mathematica求数值解也很方便，且有利于作出解的图形。在本节中，使用Laplace变换解常微分方程（组）的例子也是十分成功的，过去敬而远之的方法如今可以轻而易举的实现了。

    求准确解的函数调用格式如下：

    DSolve[eqn，y[x]，x]                                      求方程eqn的通解y（x），其中自变量是x。

    DSolve[{eqn，y[x₀]= =y₀}，y[x]，x]                       求满足初始条件y（x₀）= y₀的特解y（x）。

    DSolve[{eqn1，eqn2，…}，{y₁[x]，y₂[x]，…}，x]           求方程组的通解。

    DSolve[{equ1，…，y₁[x₀]= =y₁₀，…}，{y₁[x]，y₂[x]，…}，x]  求方程组的特解。

    说明：应当特别注意，方程及各项参数的表述方式很严格，容易出现输入错误。微分方程的表示法只有通过例题才能说清楚。

例1           解下列常微分方程（组）：

    （1），（2）， （3）  ，

    （4）的通解及满足初始条件y（0）=0，z（0）=1的特解。

  解：In[1]：=DSolve[y′[x]= =2y[x]/（x+1）+（x+1）^（5/2），

                y[x]，x]

        Out[1]=

        In[2]：=DSolve[y′[x]= =（1+y[x]^2）/((x+x^3）y[x])，y[x]，x]

        Out[2]={{}， {}}

        In[3]：=DSolve[{y′[x]= =z[x]，z′[x]= = -y[x]}，

                 {y[x]，z[x]}，x]

        Out[3]={{y[x]→C[1]Cos[x]+ C[2]Sin[x]，

                z[x]→C[2]Cos[x]- C[1]Sin[x]}}

    In[4]：=DSolve[{y′[x]= =z[x]，z′[x]= = -y[x]，y[0]= =0，z[0]= =1}，

             {y[x]，z[x]}，x]

        Out[4]={{y[x]→Sin[x]，z[x]→Cos[x]}}

    提示：认真观察上例，可以从中学习输入格式，未知函数总带有自变量，等号用连续键入两个等号表示，这两点由于不习惯会出错！导数符号用键盘上的撇号，连续两撇表示二阶导数，这与习惯相同。自变量、未知量、初始值的表示法与普通变量相同。

    说明：输出结果总是尽量用显式解表出，有时反而会使表达式变得复杂，这与教科书的习惯不同。当求显式解遇到问题时，会给出提示。通解中的任意常数用C[1]，C[2]，…表示。

例2           求解下列微分方程：

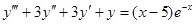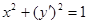  （1），（2），（3）。

解：In[1]：=DSolve[+3y″[x] +3y′[x] + y[x] = =（x - 5）Exp[-x]，

              y[x]，x]

        Out[1]={{

                    }}

        In[2]：=Simplify[%]

        Out[2]={{}}

        In[3]：=DSolve[x^2 + y′[x]^2 = = 1，y[x]，x]

        Out[3]={{}，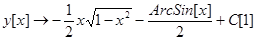

               {}}

        In[4]：=DSolve[Sqrt[y′[x]] = = x y[x]，y[x]，x]

        Out[4]={{}}

    说明：由以上可以看出对方程的类型并无限制，但是输出的答案未必符合习惯，例如第一个方程的答案需要化简，有时即使化简后也未必与教材上的答案一致。

例3           求微分方程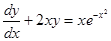的通解。

     解：In[1]：=DSolve[y^′[x]+2x y[x]= = x E^（-x^2），y[x]，x]

         Out[1]={{y[x]→}}

    这就是所给微分方程的通解。式中的C[1]是通解中的任意常数。

    上述命令也可以输入为：DSolve[D[y[x]] + 2x y[x]= =x E^（ - x^2），y[x]，x]。

例4           求微分方程xy^′+ y - e^x = 0在初始条件y|_x=1 = 2e下的特解。

     解：In[1]：=DSolve[x*y^′[x]+y[x]-E^x= =0，y[1]= =2E，y[x]，x]

         Out[1]= {{y[x]→}}

二、 常微分方程（组）的数值解

    函数NDSolve用于求给定初值条件或边界条件的常微分方程（组）的近似解，其调用格式如下：

    NDSolve[eqns，{y₁，y₂，…}，{x，xmin，xmax}]        求常微分方程（组）的近似解。

    其中微分方程和初值条件的表示法如同DSolve，未知函数仍有带自变量和不带自变量两种形式，通常使用后一种更方便。初值点x₀可以取在区间[xmin，xmax]上的任何一点处，得到插值函数InterpolatingFunction[domain，table]类型的近似解，近似解的定义域domain一般为[domain，table]，也有可能缩小。

例5           求常微分方程y′= x² + y²，满足初始条件y（0）= 0的数值解。

解：In[1]：=s1=NDSolve[{y′[x]= =x^2+y[x]^2，y[0]= =0}，

                  y，{x，-2，2}]

        Out[1]={{y→InterpolatingFunction[{{-2.，2.}}，< >]}}

        In[2]：=  y=y / . s1[[1]]

        Out[2]=InterpolatingFunction[{{-2.，2.}}，< >]

        In[3]：=Plot[y[x]，{x，-2，2}，AspectRatio→Automatic，

                PlotRange→{-1.5，1.5}]

图13-43  微分方程的解曲线

        Out[3]= -Graphics-

    上例中包含许多值得学习的实用内容，其中第二项参数使用y而不是y[x]，比用y[x]好。如果求解区间改为{x，-3，3}，就会出现警告提示，实际得不到[-3，3]上的解。Out[1]表明返回的解放在一个表中，不便使用，实际的解就是插值函数：

    InterpolatingFunction[{{-2.，2.}}，< >]

    In[2]的结果是用y表示解函数的名字，因此In[3]顺利画出解曲线如图13-43所示。

例6           求常微分方程组：

                       

 满足初始条件x（0）=0，y（0）=1的数值解。 

    解：In[1]：=s1=NDSolve[{x′[t]= = y[t] -（x[t]^3/3 - x[t]），

                        y′[t]= = - x[t]，x[0]= =0，y[0]= =1}，

                        {x，y}，{t，-15，15}]

        Out[1]={{x→InterpolatingFunction[{{-15.，15.}}，< >]，

                y→InterpolatingFunction[{{-15.，15.}}，< >]}}

        In[2]：= x=x / . s1[[1，1]]

               y=y / . s1[[1，2]]

        Out[2]=InterpolatingFunction[{{-15.，15.}}，< >]

        Out[3]=InterpolatingFunction[{{-15.，15.}}，< >]

        In[4]：=ParametricPlot[{x[t]，y[t]}，{t，-15，15}，

                   AspectRatio→Automatic]

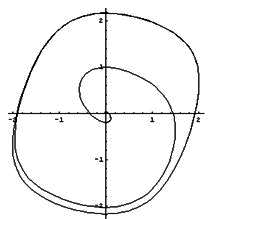
图13-44  解的相轨线

        Out[3]= -Graphics-

    说明：上例是求一个著名方程组的近似解，其中In[2]也可以改用一个赋值式{x，y}={x，y} / . Flatten[s1]，一次得到两个函数。通过求数值解容易得到它的相图，In[4]绘制了解的相轨线如图13-44所示，图中表明原点是奇点，极限环的形状也已经得到。

    为了应付复杂的情况，需要设置可选参数：

    WorkingPrecision           参见数值积分部分的介绍。

    AccuracyGoal              计算结果的绝对误差。

    PrecisionGoal               计算结果的相对误差。

    MaxSteps                  最大步数。

    StartingStepSize             初始步长。

    以上可选参数的默认值都为Automatic，其中AccuracyGoal和PrecisionGoal的默认值比WorkingPrecision小10，当解趋于0时应将AccuracyGoal取成Infinity。对于常微分方程，最大步长默认值为1000。这个函数也可以解偏微分方程，最大步长默认值为200。

例7           解下列微分方程（组）：

（1），满足初始条件y（0）=1的特解；

（2），满足初始条件x（0）=z（0）=0，y（0）=1的特解。

    解：In[1]：=NDSolve[{y′[x]= =I/4y[x]，y[0]= =1}，y，{x，1}，

                   AccuracyGoal→20，PrecisionGoal→20，WorkingPrecision→25]

        Out[1]={{y→InterpolatingFunction[

                  {{0，1.000000000000000000000000000}}，< >]}

        In[2]：=y[1] / . %

        Out[2]={0.968912424710644784118519 +

                 0.2474039592545229296234109ⅱ}

        In[3]：=NDSolve[{x′[t]= = -3（x[t] -y[t]），

                   y′[t] = = -x[t] z[t]+36.5x[t] -y[t]，

                   z′[t] = = x[t] y[t]- z[t]，

                   x[0] = = z[0] = = 0，y[0]= =1}，

                   {x，y，z}，{t，0，20}，MaxSteps→3000]

        Out[3]={{x→InterpolatingFunction[{{0.，20.}}，< >]，

                y→InterpolatingFunction[{{0.，20.}}，< >]，

                z→InterpolatingFunction[{{0.，20.}}，< >]}}，

        In[4]：=ParametricPlot3D[Evaluate[{x[t]，y[t]，z[t]} / . %]，

                   {t，0，20}，PlotPoints →1000]

图13-45  3维相轨线

        Out[3]= -Graphics3D-

说明：以上范例中In[1]取高精度，而且是复系数方程。In[2]是求解在x=1时的近似值，求精确解能得到准确值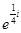，读者可以求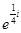的近似值与Out[2]的结果比较，验证近似解的精确度确实很高。In[3]在求解时增大步数，成功地得到了由In[4]绘制的如图13-45所示的解的相轨线。In[4]所示的绘图语句与前面例子中的不同，现在只要会模仿使用它们就行了，要想弄清原理请参阅相关Mathematica书籍。

三、 拉氏变换

    Mathematica可以进行拉普拉斯变换，其变换使用的函数调用格式如下：

    LaplaceTransform[f，t，s]              求函数f（t）的Laplace变换，返回自变量为s的函数。

    InverseLaplaceTransform[F，s，t]        求函数F（s）的Laplace逆变换，返回自变量为t的函数。

    其中函数f（t）和F（s）也可以是函数表，这样可一次变换多个函数。

例8           求函数t ⁴和e^t sint的拉氏变换。

    解：In[1]：=LaplaceTransform[t^4，t，s]

        Out[1]=

        In[2]：=LaplaceTransform[Exp[t] Sin[t]，t，s]

        Out[2]=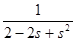

        In[3]：=InverseLaplaceTransform[%1，s，t]

        Out[3]=t⁴

        In[4]：=InverseLaplaceTransform[%2，s，t]

        Out[4]=

        In[5]：=FullSimplify[%]

        Out[5]=e^t Sin[t]

例9           求函数f（t）= t³ e^at的拉氏变换。

    解：In[1]：= LaplaceTransform[t^3 Exp[a t]，t，s]

        Out[1]=

    以上只是直接进行拉氏变换和逆变换的例子。以下使用拉氏变换解常微分方程，解法原理见本书理论篇，这里完全实现了计算机求解。

例10        用拉氏变换解微分方程：

          + 3x″+ 3x′+ x = 1满足条件x″(0) = x′(0) = x(0) = 0的解。

解：In[1]：=f1=LaplaceTransform[ [t] +3x″[t]+ 3x′[t]+x[t]，

                            t，s]

        Out[1]=LaplaceTransform[x[t]，t，s] +

                      s³LaplaceTransform[x[t]，t，s] +

                      3（sLaplaceTransform[x[t]，t，s] - x[0]）- s²x[0] +

                      3（s²LaplaceTransform[x[t]，t，s] - s x[0] - x′[0]）-

                      s x′[0]- x″[0]

        In[2]：=s1=LaplaceTransform[1，t，s]

        Out[2]=

        In[3]：= x″[0]= x′[0]= x[0]=0；

                Solve[f1= =s1，LaplaceTransform[x[t]，t，s]]

        Out[4]={{}}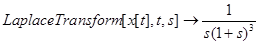

        In[5]：=InverseLaplaceTransform[，s，t]

        Out[5]=

    说明：上例中的LaplaceTransform[x[t]，t，s]就是教材中的X（s），In[3]解出X（s），其余过程与教科书完全相同。现在可以将一切计算留给计算机，学生只要弄清解法原理及过程。

    技巧：充分利用复制、粘贴功能，可以加快输入速度，避免键入错误。上例中In[5]就可以从Out[4]中将表达式复制过来。

例11  求微分方程组：

                       

           满足条件x（0）=3，x^′（0）=2，y（0）=0的特解。

解：In[1]：=f1=LaplaceTransform[

                   {x″[t] - 2x′[t] - y′[t] + 2y[t]，x′[t] + y′[t] - 2x[t]}，

                    t，s]；

        In[2]：=s1=LaplaceTransform[{0，- 2Exp[-t]}，t，s]；

        In[3]：= x[0]=3； x′[0]= 2；y[0]=0；

                Solve[{f1= =s1}，{LaplaceTransform[x[t]，t，s]，

                LaplaceTransform[y[t]，t，s]}]；

        In[5]：=InverseLaplaceTransform[

                 Flatten[

                  {LaplaceTransform[x[t]，t，s]，

                   LaplaceTransform[y[t]，t，s]} / . %]，s，t]

        Out[5]={5 - e^-t - 3e^t + 2e^2t，e^-t（- 1 +  e^t）²（1 + 2 e^t）}

        In[6]：=Simplify[%]

        Out[6]= {5 - e^-t - 3e^t + 2e^2t，e^-t - 3e^t + 2e^2t }

    说明：在上例中，不显示任何中间结果，语句比较简练。其中，In[1]和In[2]分别对方程组的左边和右边进行拉氏变换，In[3]解出X（s）和Y（s）。In[5]比较难懂，可以参看前面的例题，这里是从Out[3]中自动将解X（s）和Y（s）提取出来，再进行拉氏逆变换。Out[5]是{x（t），y（t）}，Out[6]将答案化简。本例已经将求解过程一般化，只需改变方程组和初值的数据，就可以解其它方程组了。

四、 级数

1．   求和与求积

    求有限或无穷和、积的函数是：

    Sum[f，{i，imin，imax}]                         求，其中imin可以是-∞，imax可以是∞（即+∞），但是必须满足imin≤imax。基本输入模板中也有求和专用的符号，使用模板输入更方便。

    Sum[f，{i，imin，imax}，{j，jmin，jmax}，…]    求多重和，也可以使用基本输入模板连续多次输入求和符号得到。

    Product[f，{i，imin，imax}]                      求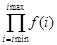，基本输入模板中也有求积符号。

    Product[f，{i，imin，imax}，{j，jmin，jmax}，…]   求多重积 ，也可以使用基本输入模板连续多次输入求积符号得到。

例12       求下列级数的和与积：

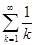  （1），（2） ，（3） ，（4） 。

    解：In[1]：=Sum[k^2，{k，1，n}]

        Out[1]=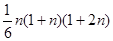

        In[2]：=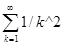

        Out[2]=

        In[3]：=

              Sum：：div：Sum does not converge.

        Out[3]=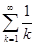

        In[4]：=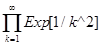

        Out[4]=

    说明：上例中第三个级数发散，Mathematica给出提示，并在不能给出结果时将输入的式子作为输出。

    NSum和NProduct得到数值解。

2．   将函数展开为幂级数

将函数展开为幂级数的函数调用格式如下：

    Series[f，{x，x₀，n}]                  将函数f（x）在x₀ 处展成幂级数直到n次项为止。

    Series[f，{x，x₀，n}，{y，y₀，m}]      将函数f（x，y）先对y后对x展开。

例13       展开下列函数为幂级数：

（1） y=tgx，（2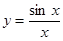） ， （3）y = f（x），（4）y = e^xy。  

    解：In[1]：=Series[Tan[x]，{x，0，9}]

        Out[1]=

        In[2]：=Series[Sin[x] /x，{x，0，9}]

        Out[2]=

        In[3]：=Series[f[x]，{x，1，7}]

        Out[3]=

              

              

        In[4]：=Series[Exp[x y]，{x，0，3}，{y，0，2}]

        Out[4]=

    说明：上例中In[3]表明也可以展开抽象的函数。

    对已经展开的幂级数进行操作的两个函数是：

    Normal[expr]                 将幂级数expr去掉余项转换成多项式。

    SeriesCoefficient[expr，n]      找出幂级数expr的n次项系数。

例14       将y = arcsinx展开为幂级数，只取前9项并去掉余项。

    解：In[1]：=Series[ArcSin[x]，{x，0，9}]

        Out[1]=

        In[2]：=Normal[%]

        Out[2]=

        In[3]：=SeriesCoefficient[%1，5]

        Out[3]=

3．   傅里叶级数

    求傅里叶级数就是求出傅里叶系数，傅里叶系数是一个积分表达式，所以利用积分函数Integrate就可以实现。

例如，设周期矩形脉冲信号的脉冲宽度为τ，脉冲幅度为E，周期为T，这种信号在一个周期[，]内的表达式为

                

    求其傅里叶级数时，可以先求出傅利叶系数。为了和Mathematica中的常数E相区分，以下用Ee表示脉冲幅度，用tao表示脉冲宽度τ，根据傅利叶系数的积分表达式，输入以下语句：

a0= 2/T Integrate[Ee，

          {t，-tao/2，tao/2}]

a[n_ ]=2/T Integrate[Ee Cos[2n Pi t/T]，

          {t，-tao/2，tao/2}]

b[n_ ]=2/T Integrate[Ee Sin[2n Pi t/T]，

           {t，-tao/2，tao/2}]

    可得到下面三个输出，即分别是a₀，a_n与b_n，即

    a₀=，a_n =与b_n=0

    从而可写出给定的傅利叶级数为：

   

习题13.5

1．求下列一阶微分方程的通解或特解。

（1）y′- 3xy = 2x；    （2）xy′+ y - e^x= 0，y|_x=a=b。

2．求下列二阶微分方程的通解或特解。

   （1）y″- 2y′+5y = 5x+2；

   （2）y″+ 2y′+2y = - e ^-x，y（0）= y′(0) = 0。

3．用拉氏变换解微分方程组：

        

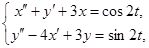
4．展开下列函数为x幂级数，并求其收敛区间。

；（2）y = cos²x；（3）y =（1 - x）ln（1 - x）

5．将函数

               

分别展开成正弦级数和余弦级数。

6．求下列函数的拉氏变换：

（1）t² + 6t - 3；（2）e^-4tsin3tcos2t；（3）。

7．求下列像函数的拉氏逆变换：

（1）F（p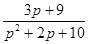）=；（2）F（p）=；

（3）F（p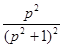）=。