实验一
一、 代码:
x=0:12;
y=0.5*erfc(sqrt(10.^(0.1*x)));
semilogy(x,y,'color','black','linewidth',2)
set(gca,'xgrid','on','ygrid','on','xcolor','red','ycolor','red');
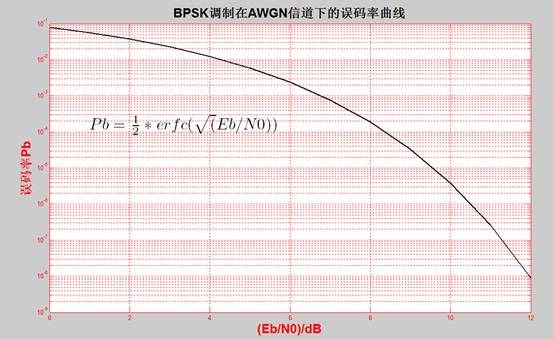
title('\bf\fontsize{20}BPSK调制在AWGN信道下的误码率曲线');
xlabel('\bf\fontsize{20} (Eb/N0)/dB');
ylabel('\bf\fontsize{20}误码率Pb');
text(1,10^-3.8,'$Pb={\frac{1}{2}}*erfc(\sqrt(Eb/N0))$','interpreter','latex',...
'fontsize',25,'color','black','FontWeight','bold')
二、 实验过程:
实验二
一、 代码:
n= 150;%阶数
fc = 5; %截止频率为5MHz
r=0.22; %滚降系数为0.22
fs= 30.72; %采样率为30.72MHz
h = firrcos(n,fc,r,fs,'rolloff','sqrt');%平方根升余弦滤波器
freqz(h) %频率响应
rand;
x=10000;
xw=randn(x,1);%高斯白噪声
figure;
plot(xw);
yw=conv(xw,h);%高斯噪声通过上述滤波器
hs = spectrum.periodogram;
psd(hs,yw)%周期图法分析其功率谱
二、 实验过程
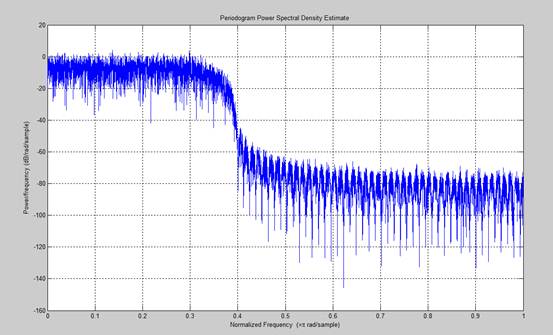
采样率为30.72MHz,截止频率为5MHz,滚降因子为0.22的平方根升余弦滤波器的幅频特性和相频特性。(上图为幅频特性,下图为相频特性)

将高斯噪声通过上述滤波器,用周期图法分析其功率谱
第二篇:现代谱估计计算机仿真实验报告
现代谱估计计算机仿真实验报告
胡敏
在许多工程应用中,利用观测到的一组样本数据估计并分析一个平稳随机信号的功率谱密度是十分重要的。例如,在雷达信号处理中,由回波信号的功率谱密度、谱峰的宽度、高度和位置,可以确定目标的位距离和运动速度;在阵列信号处理中,空间功率谱描述了信号功率随空间角度的分布情况。在许多信号处理应用中,谐波过程经常会遇到,它对应的功率谱为线谱,谐波过程的功率谱估计就是要确定谐波的个数,频率和功率(合称谐波恢复)。为了更好的学习现代信号处理中该部分的内容,我们做了相应的计算机仿真实验。
1 实验目的
1、深入理解现代谱估计和谐波恢复的基本理论,包括ARMA模型,ARMA谱估计,ARMA模型识别,Pisarenko谐波分解,信号子空间和噪声子空间,旋转不变技术(ESPRIT);
2、熟悉与上述谱估计和谐波恢复理论相关的数学方法以及各自的特点,包括最小二乘估计(LS),奇异值分解(SVD),总体最小二乘估计(TLS),特征值分解和广义特征值分解;
3、体会ARMA功率谱估计中的Cadzow谱估计子和Kaveh谱估计子,ARMA模型的识别方法,Pisarenko谐波恢复方法,ARMA建模谐波恢复方法,MUSIC方法进行谐波恢复,两种ESPRIT方法(LS-ESPRIT和TLS-ESPRIT进行谐波恢复;
2 实验原理
2.1 ARMA谱估计
相当多的平稳随机过程都可以通过用白噪声激励线性时不变系统来产生,而线性系统又可以用线性差分方程进行描述,这种差分模型就是自回归—滑动平均(ARMA)模型。而且,任何一个有理式的功率谱密度都可以用一个ARMA随机过程的功率谱密度精确逼近。ARMA随机过程定义为服足下列线性差分方程的离散随机过程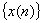 :
:
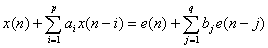 (1)
(1)
式中 是一离散白噪声;式(1)所示的差分方程称为ARMA模型,系统
是一离散白噪声;式(1)所示的差分方程称为ARMA模型,系统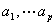 和
和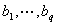 分别称为自回归(AR)参数和滑动平均(MA)参数,而
分别称为自回归(AR)参数和滑动平均(MA)参数,而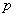 和
和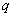 分别叫做AR阶数和MA阶数。ARMA过程
分别叫做AR阶数和MA阶数。ARMA过程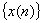 可以简记为ARMA
可以简记为ARMA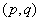 ,使用移位算子
,使用移位算子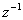 可以把它写作如下形式:
可以把它写作如下形式:
 (2)
(2)
其中: 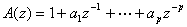
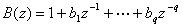
若 ,则平稳ARMA
,则平稳ARMA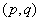 过程的功率谱密度为:
过程的功率谱密度为:
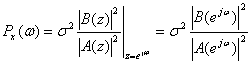 (3)
(3)
用(3)式进行谱估计必须事先辨识ARMA 模型和激励噪声的方差 ,而MA参数的估计需要求解非线性方程。为了避开非线性运算,Cadzow和Kaveh分别提出了一种线性谱估计子:
,而MA参数的估计需要求解非线性方程。为了避开非线性运算,Cadzow和Kaveh分别提出了一种线性谱估计子:
1、Cadzow谱估计子
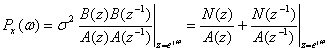 (4)
(4)
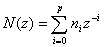 (5)
(5)
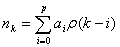
 (6)
(6)
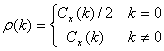 (7)
(7)
其中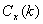 为
为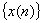 的协方差函数。因此用Cadzow谱估计子只需要确定AR阶数和AR参数就能进行ARMA谱估计。
的协方差函数。因此用Cadzow谱估计子只需要确定AR阶数和AR参数就能进行ARMA谱估计。
2、Kaveh谱估计子
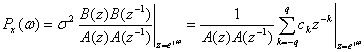 (8)
(8)
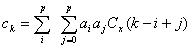
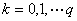 (9)
(9)
Kaveh谱估计子需要确定AR阶数,AR参数和MA阶数来进行ARMA谱估计。
3、AR阶数和参数的确定
对于一个ARMA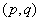 过程,可以推出其相关函数满足如下方程:
过程,可以推出其相关函数满足如下方程:
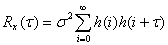 (10)
(10)
其中 为系统的冲激响应,根据其定义可以得到:
为系统的冲激响应,根据其定义可以得到:
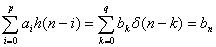 (11)
(11)
由(10)式和(11)式就能推导得到著名的修正Yule-Walker方程,简称MYW方程:
 ,
, (12)
(12)
若已知AR阶数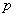 ,就能通过求解
,就能通过求解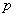 个MYW方程来求解AR参数:
个MYW方程来求解AR参数:
 (13)
(13)
其中: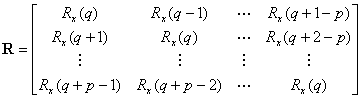

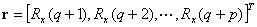
该方程可以用最小二乘法估计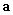 的值:
的值:
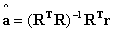 (14)
(14)
而实际问题中,AR阶数往往是未知的,此时可用奇异值分解法确定AR阶数,总体最小二乘估计AR参数,合称SVD-TLS算法。考虑超定方程:
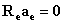 (15)
(15)
其中: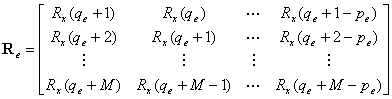

 ,
,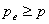 ,
, 。若
。若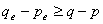 ,就可以通过对
,就可以通过对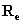 奇异值分解:
奇异值分解:
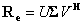 (16)
(16)
 中包含
中包含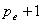 个奇异值,将其归一化:
个奇异值,将其归一化:
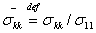 ,
, (17)
(17)
选择一个接近于零的数作为阈值,把 大于此值得最大整数
大于此值得最大整数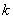 作为有效秩
作为有效秩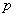 ,它就是AR阶数。
,它就是AR阶数。
根据总体最小二乘方法可以得到矩阵:
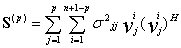 (18)
(18)
其中: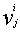 是酉矩阵
是酉矩阵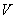 第
第 列的一个加窗段,定义为:
列的一个加窗段,定义为:
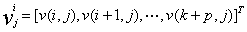 (19)
(19)
由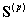 的
的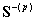 可以估计AR参数为:
可以估计AR参数为:
 ,
,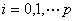 (20)
(20)
4、MA阶数和参数的确定
在AR定阶和参数估计的SVD-TLS算法中,取 ,令
,令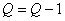 ,构造超定矩阵:
,构造超定矩阵:

 。计算其SVD,计算比值:
。计算其SVD,计算比值:
 (21)
(21)
式中 是
是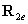 对应
对应 的第
的第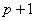 个奇异值,若
个奇异值,若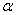 大于某个给定的阈值,则接受
大于某个给定的阈值,则接受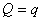 。
。
在推导Kaveh估计子的过程中可以得到一组非线性方程组,使用Newton-Raphson算法求解该方程组可以得到MA参数,其过程如下:
(1)、令MA参数的初始值为: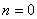 ,
,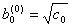 ,
, ,
,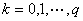
(2)、计算 迭代的拟合误差函数:
迭代的拟合误差函数:
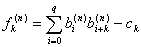 ,
,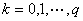 (22)
(22)
式中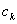 可由(9)式求解。
可由(9)式求解。
(3)计算矩阵:
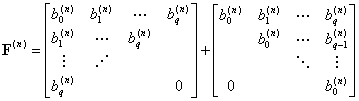
(4)更新MA参数估计向量:
 (23)
(23)
(5)判断MA参数估计向量是否收敛,若收敛,则迭代停止,若发散,令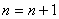 返回(2)计算,直到MA参数估计收敛为止。
返回(2)计算,直到MA参数估计收敛为止。
2.2 Pisarenko谐波分解理论
考虑由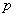 个无重复频率的正弦波组成的过程:
个无重复频率的正弦波组成的过程:
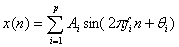 (24)
(24)
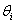 是在
是在 内均匀分布的随机数,则其
内均匀分布的随机数,则其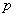 个频率由特征多项式:
个频率由特征多项式:
 ,
,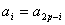 ,
,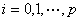 (25)
(25)
的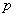 对共轭复根决定。一般在加性白噪声
对共轭复根决定。一般在加性白噪声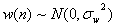 中观测该过程,所以观测过程
中观测该过程,所以观测过程 是一个特殊的ARMA
是一个特殊的ARMA 过程,且AR参数和MA参数完全相等。在使用
过程,且AR参数和MA参数完全相等。在使用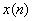 和
和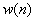 统计独立的假设下,可以得到一个重要的法方程:
统计独立的假设下,可以得到一个重要的法方程:
 (26)
(26)
其中: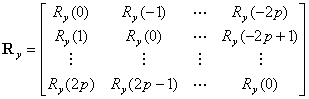

这表明 是观测过程
是观测过程 的自相关矩阵
的自相关矩阵 的特征值,其对应的特征向量正好是特征多项式(25)的系数,Pisarenko谐波分解法的思想就是找出
的特征值,其对应的特征向量正好是特征多项式(25)的系数,Pisarenko谐波分解法的思想就是找出 最小的特征值并将其对应的特征向量代入(25)式以求得
最小的特征值并将其对应的特征向量代入(25)式以求得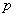 对共轭复根,再由下式确定频率:
对共轭复根,再由下式确定频率:
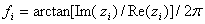 (27)
(27)
2.3 ARMA建模法谐波恢复
2.2中分析的ARMA 过程不满足MYW方程的条件,但可以推导出其服从的法方程和MYW方程的形式是一致的,所以谐波恢复的ARMA建模算法如下:
过程不满足MYW方程的条件,但可以推导出其服从的法方程和MYW方程的形式是一致的,所以谐波恢复的ARMA建模算法如下:
(1)利用观测数据计算样本自相关矩阵:

其中: ,
, ;
;
(2)用SVD-TLS算法确定AR阶数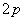 和系数向量
和系数向量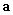 的总体最小二乘估计;
的总体最小二乘估计;
(3)计算特征多项式(25)的共轭根对(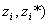 ,有(27)式确定频率。
,有(27)式确定频率。
2.4 MUSIC方法
考虑白噪声中的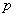 个谐波信号
个谐波信号
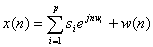 ,
,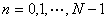 (28)
(28)
 ,引入以下向量:
,引入以下向量:
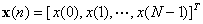

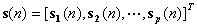
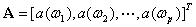
则有:
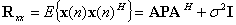 (29)
(29)

对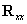 进行特征值分解得到:
进行特征值分解得到:
 (30)
(30)
式中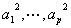 是无加性噪声时信号自相关矩阵的特征值。所以
是无加性噪声时信号自相关矩阵的特征值。所以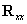 的特征值由
的特征值由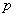 个信号特征值和
个信号特征值和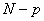 个噪声特征值组成,与此对应把特征向量矩阵的列向量分为两部分,即
个噪声特征值组成,与此对应把特征向量矩阵的列向量分为两部分,即

分别称为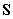 和
和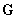 分别由信号特征向量和噪声特征向量组成;由
分别由信号特征向量和噪声特征向量组成;由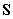 和
和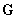 分别张成的空间分别叫做信号子空间和噪声子空间。
分别张成的空间分别叫做信号子空间和噪声子空间。
可以推导出:
 (31)
(31)
所以用MUSIC方法进行谐波恢复的思想是:以很小的步长对 进行搜索,寻找
进行搜索,寻找
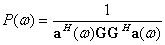 (32)
(32)
或 (33)
(33)
的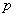 个极大值点,其对应的频率就是所求的谐波频率。
个极大值点,其对应的频率就是所求的谐波频率。
2.5 旋转不变技术ESPRIT
2.4中描述的问题,引入向量:





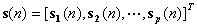

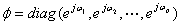
于是有:
 (34)
(34)
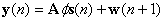 (35)
(35)
酉矩阵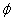 称为旋转算符,在上面描述的过程
称为旋转算符,在上面描述的过程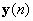 是
是 平移的结果,可以看作是最简单的旋转。
平移的结果,可以看作是最简单的旋转。
向量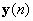 和
和 的互相关矩阵为:
的互相关矩阵为:
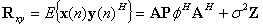 (36)
(36)
其中: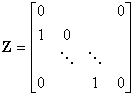
因为平移保持了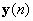 和
和 信号子空间的不变性,所以可以构造矩阵束
信号子空间的不变性,所以可以构造矩阵束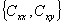 :
:
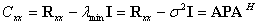
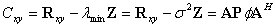
其中 是
是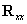 的最小特征值。对矩阵束
的最小特征值。对矩阵束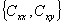 进行广义特征值分解,其特征值矩阵
进行广义特征值分解,其特征值矩阵 与矩阵
与矩阵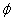 有如下关系:
有如下关系:
 (37)
(37)
基本ESPRIT算法(LS-ESPRIT算法)的思想就是用矩阵束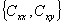 的广义特征值矩阵的前
的广义特征值矩阵的前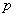 个特征值来估计谐波频率,计算公式使用(27)式。
个特征值来估计谐波频率,计算公式使用(27)式。
TLS-ESPRIT算法的思想是:对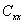 进行奇异值分解,确定有效秩
进行奇异值分解,确定有效秩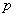 ,并存储与
,并存储与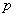 个主奇异值对应的
个主奇异值对应的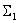 ,
,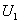 和
和 ;求
;求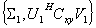 的广义特征值分解,得到
的广义特征值分解,得到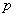 个广义特征值,它们给出了
个广义特征值,它们给出了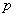 个谐波频率。
个谐波频率。
3 实验内容
仿真的观测数据由下式给出:
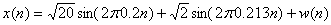
其中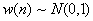 是一列高斯白噪声,
是一列高斯白噪声,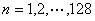 。进行如下各项实验:
。进行如下各项实验:
1、 取AR阶数分别为4和6,用最小二乘法估计AR参数,然后使用Cadzow谱估计子进行功率谱估计,并试根据该谱确定谐波频率;
2、 假定AR阶数未知,用SVD-TLS方法确定AR阶数和参数,然后使用Cadzow谱估计子进行功率谱估计,并试根据该谱确定谐波频率;
3、 用ZHANG方法确定MA阶数,用Kaveh谱估计子进行功率谱估计,用Newton-Raphson方法估计MA参数,结合2确定ARMA模型,计算ARMA功率谱,并试根据该谱确定谐波频率;
4、 用Pisarenko谐波恢复方法确定谐波频率;
5、 用ARMA建模谐波恢复方法确定谐波频率;
6、 用MUSIC方法确定谐波频率;
7、 用LS-ESPRIT方法确定谐波频率;
8、 用TLS-ESPRIT方法确定谐波频率。
4 实验过程
1、编写基于最小二乘法和Cadzow谱估计子的计算机仿真程序lsestimate.m(代码见附录1),独立运行程序5次,表1给出了频率的估计数据。从表中数据可以看出第三次程序运行效果比较理想,图1所示的是这次仿真得到的功率谱估计结果。
表1 LS法+Cadzow估计子得到的频率估计数据

取出奇点0.3125,0.2891,0.2578,0.2656,0.1484后,计算数据计算方差和均值得到:
均值:m=0.2015
方差:s=0.0032
2、编写用SVD-TLS方法确定AR阶数和参数,ZHANG方法确定MA阶数,Newton-Raphson方法估计MA参数,用Cadzow谱估计子,Kaveh谱估计子,ARMA模型三种方法估计功率谱的程序svdtls.m(代码见附录2)。表2给出了独立运行计算机仿真程序20次的结果。图2给出了程序第二次运行和第十八次运行得到的用三种方法估计的功率谱。
去除奇点计算数据均值和方差:
均值:m_Cadzow=0.2008, m_ARMA=0.2013, m_Kaveh=0.2013
方差:s_Cadzow=0.0032, s_ARMA=0, s_Kaveh=0

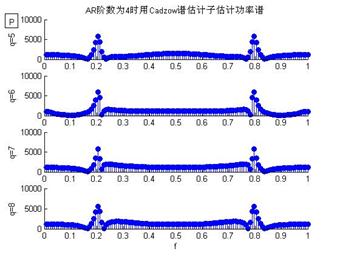
图1 AR阶数为4和6时,LS+Cadzow估计子得到的功率谱
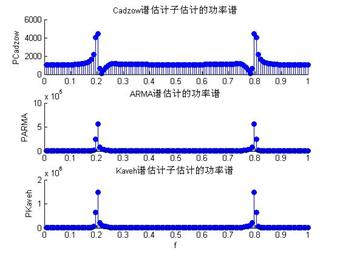
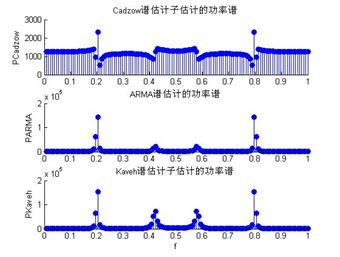
图2 TLS+Cadzow估计子+Kaveh估计子+ARMA得到的功率谱
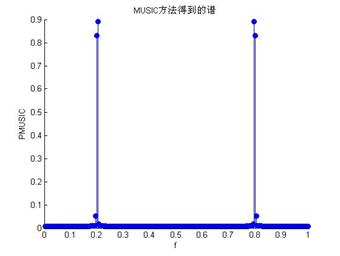
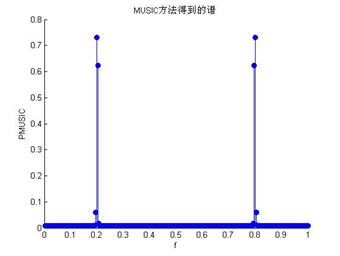
图3 MUSIC方法得到的谱
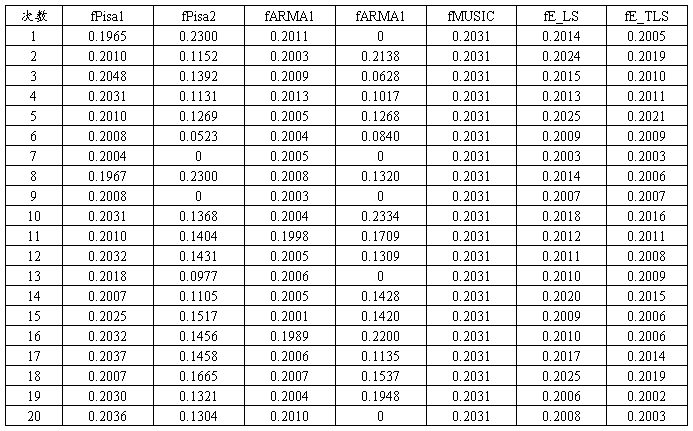
3、编写基于Pisarenko谐波分解,ARMA建模方法、MUSIC方法、ESPRIT方法估计谐波频率的计算机仿真程序sinrecover.m(代码见附录3),独立运行程序20次,表一给出了每次的频率估计结果。图3两次仿真中用MUSIC方法得到的谱。
去除奇点计算数据均值和方差:
均值:
m_Pisarenko=0.2016,m_ARMA=0.2005,m_MUSIC=0.2031,m_ESPRIT_LS=0.2014, m_ESPRIT_TLS=0.2010
方差:s_Pisarenko=0.0021,s_ARMA=0.0005,s_MUSIC=0,s_ESPRIT_LS=0.0006,s_ESPRIT_TLS=0.0005
表2、20次运行svdtls.m得到数据
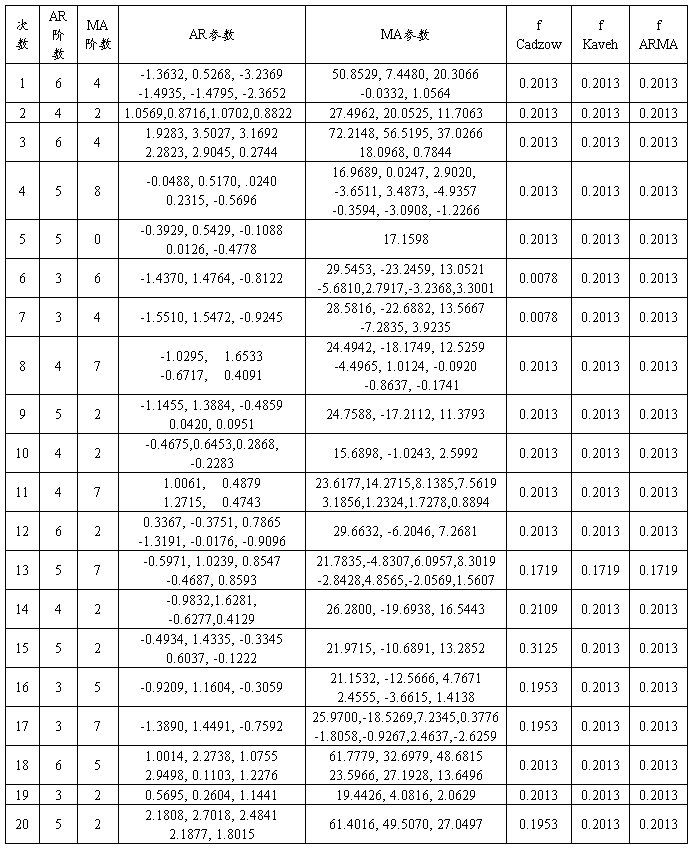
表3、20次运行程序sinrecover.m得到的频率估计数据
5 实验讨论
5.1 一般最小二乘估计和总体最小二乘估计的比较
实验过程中发现的第一个问题是,LS估计的数值稳定性不如TLS。LS方法估计的结果出现歧点的频率比较高,而TLS方法后频率估计只出现一次歧点。在实验程序中增加三种试验:1、减少噪声的影响(将噪声电平减少十倍),发现这样对LS法的数值稳定性改变很小;2、把样本数量增加一倍后,运行结果出现歧点的次数明显减少。分析原因,是因为样本数量的增加提高自相关矩阵估计的精确度,因为LS法中使用的矩阵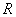 理论上是满秩的,但自相关函数计算所使用的估计子是渐进无偏估计,加上噪声的影响,可能导致矩阵
理论上是满秩的,但自相关函数计算所使用的估计子是渐进无偏估计,加上噪声的影响,可能导致矩阵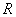 亏缺,致使最终结果的不稳定,所以大样本可提高估计准确度;3、增大
亏缺,致使最终结果的不稳定,所以大样本可提高估计准确度;3、增大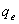 ,估计错误率的提高,使用MYW方程时,
,估计错误率的提高,使用MYW方程时,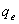 选择(即方程组选择的起点)理论上只要大于实际的
选择(即方程组选择的起点)理论上只要大于实际的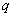 值就能进行准确估计,但实验结果并非如此,究其原因还是跟自相关函数估计子有关,因为随着数据间隔的增加,实际参加计算的样本数在减少,而自相关函数估计子中使用的样本数
值就能进行准确估计,但实验结果并非如此,究其原因还是跟自相关函数估计子有关,因为随着数据间隔的增加,实际参加计算的样本数在减少,而自相关函数估计子中使用的样本数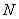 是不变的,所以当自相关函数偏离零点越远是,估计值就越小于实际值,而且受噪声的影响就越大。
是不变的,所以当自相关函数偏离零点越远是,估计值就越小于实际值,而且受噪声的影响就越大。
TLS法的合理的原因就在于同时考虑了MYW方程中样本相关矩阵的误差和方程右边样本相关向量的误差(LS法中只认为方程右边样本相关向量含有误差),也就是考虑了总体的误差,实验结果也证明了这么做的合理性。在后面ARMA建模或TLS-ESPRIT谐波恢复方法的应用中也证明了TLS这种合理性,可以看出TLS-ESPRIT估计的频率偏差和方差明显优于LS-ESPRIT得到的结果。
5.2 三种功率谱估计方法的比较
比较几幅图像,首先看到是Cadzow估计子有明显的能量泄漏(或者称频率泄漏)现象,即频谱上没有出现正弦波应有理想线谱,而在整个频域内都有能量分布,第一个原因当然有噪声的影响,但是从后面的Kaveh估计子和ARMA模型估计的频谱中可以看出,在如此高的信噪比条件(10dB)下噪声的影响是很小的,所以主要原因肯定是由算法导致的:
对于Cadzow估计子,从(4)可以看出它为了避开MA参数估计的非线性计算,把噪声方差和MA参数都整合到另外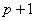 个参数
个参数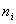 (
(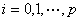 )中,这样做的缺陷是忽略了MA阶数的影响,在
)中,这样做的缺陷是忽略了MA阶数的影响,在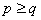 的情况下可以把这个过程理解为有理式的部分分式分解,但如果
的情况下可以把这个过程理解为有理式的部分分式分解,但如果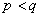 ,这么做显然是不合理的,至少对增加
,这么做显然是不合理的,至少对增加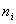 的个数来使(4)式成立。
的个数来使(4)式成立。
Kaveh估计子在这方面做了改进,至少考虑了MA阶数的影响,从(8)式可以看出Kaveh估计子把噪声方差和MA参数都整合到另外 个参数
个参数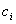 (
( )中。考虑到实验中的噪声方差是1,这部分的影响也可以忽略,所以其效果可以达到与ARMA模型(考虑AR阶数和系数,MA阶数和系数)相比拟的程度。在实验中改变噪声方差后,就能发现Kaveh 估计子不如ARMA模型理想。
)中。考虑到实验中的噪声方差是1,这部分的影响也可以忽略,所以其效果可以达到与ARMA模型(考虑AR阶数和系数,MA阶数和系数)相比拟的程度。在实验中改变噪声方差后,就能发现Kaveh 估计子不如ARMA模型理想。
5.3 四种谐波恢复方法的比较
首先注意到实验中的谐波信号是确定性信号,不能满足平稳随机过程的条件,而且是相关的。所以用平稳随机过程和不相关信号的处理方法来估计信号功率是行不通的,所以实验中的谐波恢复只是估计了谐波的频率。
Pisarenko谐波分解法遇到问题是在矩阵 的所有特征值中如何确定哪个是噪声方差对应的特征值,实验程序中的方法是选最小的那个特征值,这样做显然是不合理的,从信号子空间和噪声子空间的理论分析中可知,对于实验中的信号,谐波信号对应的特征值只有四个,如果事先不知道谐波个数的话,就必须构造超定的矩阵
的所有特征值中如何确定哪个是噪声方差对应的特征值,实验程序中的方法是选最小的那个特征值,这样做显然是不合理的,从信号子空间和噪声子空间的理论分析中可知,对于实验中的信号,谐波信号对应的特征值只有四个,如果事先不知道谐波个数的话,就必须构造超定的矩阵 来进行处理,其对应有多个最小的特征值,所以就必须逐步进行降维处理,直到只有一个最小的特征值,这个过程的实现是相当困难的,因为只有一个最小的判定条件根本就无法量化,但实验程序中假设谐波个数已知的条件下,发现其估计准确率还是很高的。
来进行处理,其对应有多个最小的特征值,所以就必须逐步进行降维处理,直到只有一个最小的特征值,这个过程的实现是相当困难的,因为只有一个最小的判定条件根本就无法量化,但实验程序中假设谐波个数已知的条件下,发现其估计准确率还是很高的。
ARMA建模法可以取得较好的效果,得益于SVD较好估计了谐波的个数,TLS能较好估计特征多项式的系数向量。
MUSIC方法和ESPRIT的方法能准确地估计谐波的频率,但是MUSIC方法对噪声处理能力不如ESPRIT方法,这点在5.5中讨论。
5.4 关于频率分辨率
提高第二个谐波的幅度跟第一个谐波一致,进行实验,发现从功率谱上还是不能发现第二个谐波,所以谱估计对频率的分辨率是有限的,这个限度一方面跟谱估计子有关,一方面跟计算谱值的点数有关,点数增加可以提高分辨率。将第二频率提高到0.25以上,就能实现较好的分离,图四给出了提高频率间隔前后的谱估计图像。
相比之下,几种谐波恢复方法(除了Pisarenko方法)的频率分辨率都比较高,特别是在增加样本数据点的情况下,除了Pisarenko方法经常出现歧点(我觉得原因开自方法本身的局限性)外,其它几种方法都能准确地进行频率估计。
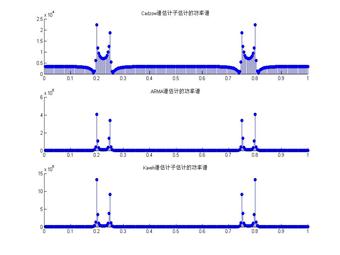

图3 提高频率间隔前后的功率谱估计图
5.5 关于信噪比
提高另一个谐波的频率到0.313,观察信噪比对上述方法的影响。实际上,模拟观测信号中,第二个谐波与噪声的信噪比是0dB,但发现三种谱估计方法有较强的去噪声能力,图4中给出了三种谱估计方法在信噪比0dB的条件下发现信号的情景。
相比之下,四种谐波恢复方法噪声背景的处理能力比较弱。特别是MUSIC方法,只有当信噪比提高到5dB以上才能进行正确的频率分离。图5给出了提高信噪比到10dB后,MUSIC方法得到的谱。
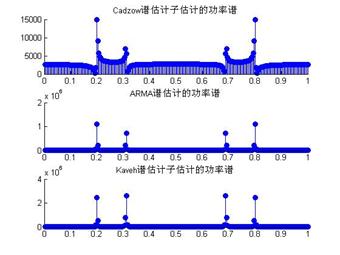
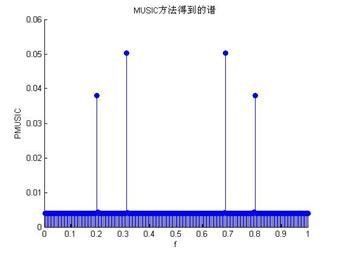
图4 谱估计方法在信噪比0dB下发现信号 图5 MUSIC方法在提高信噪比后发现信号
5.6 关于几个阈值的选取
程序编写中发现阈值的取法并没有固定的标准,教材上给出阈值的例子在实验中计算效果并不很理想,所以阈值应该针对特点的问题来选取,本实验中确定阈值的方法是:先运行几次程序,观察实验数据,选择一个可行的数作为阈值,然后经过多次尝试调整之后取定的。
附录
1、程序lsestimate.m
clc,clear;
t=1:128;%数据时间向量
N=length(t);%数据个数
f=t/N;%频率向量
w=2*pi*f;%角频率向量
z=exp(j*w);
randn('state',sum(100*clock));%每次计算给随机数产生设置不同的起点
wn=randn(size(t));%功率为1的高斯白噪声
x=sqrt(20)*sin(2*pi*0.2*t)+sqrt(2)*sin(2*pi*0.213*t)+wn;%观测数据
%估计自相关函数
R=xcorr(x);
%估计协方差函数
COR=xcov(x);
CORP=COR;
CORP(N)=COR(N)/2;
%用一般最小二乘法估计功率谱和谐波频率
pls=4;%AR模型的阶数取4
for qels=5:8;%选取修正Yule-Walker方程的起点
%以下求相关函数估计值组成的Hankel矩阵
RLS4=R(qels:(qels+pls-1));
for k=1:(pls-1)
RLS4=[R((qels-k):(qels-k+pls-1));RLS4];
end
bls4=-R((qels+1):(qels+pls));%Yule-Walker方程右边的值
als4(:,(qels-pls))=(RLS4'*RLS4)^(-1)*RLS4'*(bls4)';%最小二乘估计公式
end
display('AR阶数为4,qe取5,6,7,8时,用一般最小二乘法估计的AR参数:')
als4=als4(pls:-1:1,:)
%采用Cadzow谱估计子进行功率谱估计
als4=[ones(1,4);als4];
als4=als4';
CCadzowp4=CORP(N:N+pls);
for i=1:pls
CCadzowp4=[CCadzowp4;CORP(N-i:N-i+pls)];
end
nCadzowp4=als4*CCadzowp4;
Nzp4=zeros(4,N);
Azp4=zeros(4,N);
Nnzp4=zeros(4,N);
Anzp4=zeros(4,N);
for k=0:pls
Nzp4=Nzp4+nCadzowp4(:,k+1)*(z.^(-k));
Azp4=Azp4+als4(:,k+1)*(z.^(-k));
Nnzp4=Nnzp4+nCadzowp4(:,k+1)*(z.^k);
Anzp4=Anzp4+als4(:,k+1)*(z.^k);
end
PWxCadzowp4=Nzp4./Azp4+Nnzp4./Anzp4;
PWxCadzowp4=abs(PWxCadzowp4);
figure(1);
for i=1:4
subplot(4,1,i);
stem(f,PWxCadzowp4(i,:),'filled');
flsp4(i)=find(PWxCadzowp4(i,1:(N/2-1))==max(PWxCadzowp4(i,1:(N/2-1))))/N;
end
display('AR阶数为6,qe取7,6,7,8时,用Cadzow谱估计子估计频率:')
flsp4
pls=6;%AR模型的阶数取6
for qels=7:10;%选取修正Yule-Walker方程的起点
%以下求相关函数估计值组成的Hankel矩阵
RLS6=R(qels:(qels+pls-1));
for k=1:(pls-1)
RLS6=[R((qels-k):(qels-k+pls-1));RLS6];
end
bls6=-R((qels+1):(qels+pls));%Yule-Walker方程右边的值
als6(:,(qels-pls))=(RLS6'*RLS6)^(-1)*RLS6'*(bls6)';%最小二乘估计公式
end
display('AR阶数为6,qe取7,8,9,10时,用一般最小二乘法估计的AR参数:')
als6=als6(pls:-1:1,:)
%采用Cadzow谱估计子进行功率谱估计
als6=[ones(1,4);als6];
als6=als6';
CCadzowp6=CORP(N:N+pls);
for i=1:pls
CCadzowp6=[CCadzowp6;CORP(N-i:N-i+pls)];
end
nCadzowp6=als6*CCadzowp6;
Nzp6=zeros(4,N);
Azp6=zeros(4,N);
Nnzp6=zeros(4,N);
Anzp6=zeros(4,N);
for k=0:pls
Nzp6=Nzp6+nCadzowp6(:,k+1)*(z.^(-k));
Azp6=Azp6+als6(:,k+1)*(z.^(-k));
Nnzp6=Nnzp6+nCadzowp6(:,k+1)*(z.^k);
Anzp6=Anzp6+als6(:,k+1)*(z.^k);
end
PWxCadzowp6=Nzp6./Azp6+Nnzp6./Anzp6;
PWxCadzowp6=abs(PWxCadzowp6);
figure(2);
for i=1:4
subplot(4,1,i);
stem(f,PWxCadzowp6(i,:),'filled');
flsp6(i)=find(PWxCadzowp6(i,1:(N/2-1))==max(PWxCadzowp6(i,1:(N/2-1))))/N;
end
display('AR阶数为6,qe取7,8,9,10时,用Cadzow谱估计子估计频率:')
flsp6
2、程序svdtls.m
clc,clear;
t=1:128;%数据时间向量
N=length(t);%数据个数
f=t/N;%频率向量
w=2*pi*f;%角频率向量
z=exp(j*w);
randn('state',sum(100*clock));%每次计算给随机数产生设置不同的起点
wn=randn(size(t));%功率为1的高斯白噪声
x=sqrt(20)*sin(2*pi*0.2*t)+sqrt(2)*sin(2*pi*0.213*t)+wn;%观测数据
%估计自相关函数
R=xcorr(x);
%估计协方差函数
COR=xcov(x);
CORP=COR;
CORP(N)=COR(N)/2;
%用SVD-TLS法估计功率谱和谐波频率
peTLS=6;
qeTLS=10;%选取修正Yule-Walker方程的起点
%以下求增广矩阵
RTLS=R((N+qeTLS+1):-1:(N+qeTLS+1-peTLS));
for k=2:(peTLS+2)
RTLS=[RTLS;R((N+qeTLS+k):-1:(N+qeTLS+k-peTLS))];
end
%以下对RTLS做奇异值分解SVD
[UTLS STLS VTLS]=svd(RTLS);
%奇异值归一化,并确定有效秩p
STLS1=STLS/STLS(1,1);
pTLS=0;
k=peTLS;
while pTLS==0
if STLS1(k,k)>=0.005
pTLS=k;
else
k=k-1;
end
end
display('SVD-TLS法确定的AR阶数为:')
pTLS
%计算Sp
SpTLS=zeros(pTLS+1,pTLS+1);
for i=1:pTLS
for k=1:(peTLS+1-pTLS)
SpTLS=SpTLS+STLS(i,i)*VTLS(k:k+pTLS,i)*(VTLS(k:k+pTLS,i))';
end
end
%AR参数的估计值为:
SpnTLS=SpTLS^(-1);
aTLS=SpnTLS(:,1)/SpnTLS(1,1);
display('SVD-TLS法确定的AR参数为:')
aTLS
%采用Cadzow谱估计子进行功率谱估计
CCadzow=CORP(N:N+pTLS);
for i=1:pTLS
CCadzow=[CCadzow;CORP(N-i:N-i+pTLS)];
end
nCadzow=aTLS'*CCadzow;
Nz=zeros(1,N);
Az=zeros(1,N);
Nnz=zeros(1,N);
Anz=zeros(1,N);
for k=0:pTLS
Nz=Nz+nCadzow(k+1)*(z.^(-k));
Az=Az+aTLS(k+1)*(z.^(-k));
Nnz=Nnz+nCadzow(k+1)*(z.^k);
Anz=Anz+aTLS(k+1)*(z.^k);
end
PWxCadzow=Nz./Az+Nnz./Anz;
PWxCadzow=abs(PWxCadzow);
subplot(3,1,1);
stem(f,PWxCadzow,'filled');
title('Cadzow谱估计子估计的功率谱');
%通过功率谱估计频率
display('Cadzow谱估计子估计的频率:')
fCadzow=find(PWxCadzow(1:(N/2-1))==max(PWxCadzow(1:(N/2-1))))/N
%MA阶数和参数的辨识
Q=qeTLS;%Q=qe>q
%以下求增广矩阵
RTLStemp=R((N+Q):-1:(N+Q-pTLS));
for i=1:(pTLS+5) % 使RTLStemp为超定矩阵
RTLStemp=[RTLStemp;R((N+Q+i):-1:(N+Q+i-pTLS))];
end
[UTLStemp STLStemp VTLStemp]=svd(RTLStemp);
OQ1=STLStemp(pTLS+1,pTLS+1);
flag=0;
while flag<=0.3
%以下求增广矩阵
Q=Q-1;
RTLStemp=R((N+Q):-1:(N+Q-pTLS));
for i=1:(pTLS+5) % 使RTLStemp为超定矩阵
RTLStemp=[RTLStemp;R((N+Q+i):-1:(N+Q+i-pTLS))];
end
[UTLStemp STLStemp VTLStemp]=svd(RTLStemp);
OQ2=STLStemp(pTLS+1,pTLS+1);
flag=abs((OQ1-OQ2)/OQ2);
qTLS=Q;
end
display('zhang方法确定的MA阶数为:')
qTLS
%Kaveh估计子系数和Newton-Raphson算法估计MA系数
ck=zeros(qTLS+1,1);
for k=1:(qTLS+1)
for m=1:pTLS+1
for n=1:pTLS+1
ck(k)=ck(k)+aTLS(m)*conj(aTLS(n))*COR(N+k-1+n-m);
end
end
end
%Newton-Raphson算法
bNewton=zeros(qTLS+1,1);
%以下是MA系数的初始值
biNewton=[ck(1)^(1/2);zeros(qTLS,1)];
while min(abs(bNewton))==0
%以下是第i次的拟合误差函数
I=find(abs(bNewton)~=0);
biNewton(I)=0;
biNewton=biNewton+bNewton;
fki=-ck;
for k=1:qTLS+1
for m=1:(qTLS+2-k)
fki(k)=fki(k)+biNewton(m)*biNewton(m+k-1);
end
end
Fi=hankel(biNewton)+rot90(hankel(biNewton(qTLS+1:-1:1)),3);
%以下是第i+1次跌代的MA系数
bi1=biNewton-Fi^(-1)*fki;
bNewton=bi1;
%判断第i+1次跌代的MA系数的收敛性
for k=1:qTLS+1
if abs((bi1(k)-biNewton(k))/bi1(k))<=0.05
bNewton(k)=bi1(k);
end
end
biNewton=bi1;
end
display('Newton-Raphson算法确定的MA参数为:')
bNewton
%用ARMA模型和Kaveh估计子进行功率谱估计
Bz=zeros(1,N);
Cz=zeros(1,N);
Bnz=zeros(1,N);
Cnz=zeros(1,N);
for k=0:qTLS
Bz=Bz+bNewton(k+1)*(z.^(-k));
Cz=Cz+ck(k+1)*(z.^(-k));
Bnz=Bnz+bNewton(k+1)*(z.^k);
Cnz=Cnz+ck(k+1)*(z.^k);
end
Cz(1)=Cz(1)/2;
Cnz(1)=Cnz(1)/2;
%ARMA模型功率谱估计
PWxzARMA=(Bz.*Bnz)./(Az.*Anz);
PWx=abs(PWxzARMA);
subplot(3,1,2);
stem(f,PWx,'filled');
title('ARMA谱估计的功率谱');
%通过功率谱估计频率
display('ARMA谱估计的频率:')
fARMAP=find(PWx(1:(N/2-1))==max(PWx(1:(N/2-1))))/N
%Kaveh估计子功率谱估计
PWxzKaveh=(Cz+Cnz)./(Az.^2);
PWx=abs(PWxzKaveh);
subplot(3,1,3);
stem(f,PWx,'filled');
title('Kaveh谱估计子估计的功率谱');
%通过功率谱估计频率
display('Kaveh谱估计子估计的频率:')
fKaveh=find(PWx(1:(N/2-1))==max(PWx(1:(N/2-1))))/N
3、程序sinrecover.m
clc,clear;
t=1:128;%数据时间向量
N=length(t);%数据个数
randn('state',sum(100*clock));%每次计算给随机数产生设置不同的起点
wn=randn(size(t));%功率为1的高斯白噪声
x=sqrt(20)*sin(2*pi*0.2*t)+sqrt(2)*sin(2*pi*0.213*t)+wn;%观测数据
%估计自相关函数
R=xcorr(x);
%Pisarenko谐波分解及恢复
psin=2;%若已知正弦波个数为2
%以下求观测数据相关函数矩阵
RPisa=rot90(hankel(R((N+2*psin):-1:N),R(N:-1:(N-2*psin))));
[XPisa,DPisa]=eig(RPisa);
aPisa=XPisa(:,2*psin+1);
rPisa=roots(aPisa);
fPisa=atan(abs(imag(rPisa)./real(rPisa)))/(2*pi)
%ARMA建模法谐波恢复
pe=6;
M=10;%M>>p
%以下求增广矩阵
RARMA=R((N+pe+1):-1:(N+1));
for i=2:M
RARMA=[RARMA;R((N+pe+i):-1:(N+i))];
end
%以下对RARMA做奇异值分解SVD
[UA SA VA]=svd(RARMA);
%奇异值归一化,并确定有效秩p
SA1=SA/SA(1,1);
pARMA=0;
i=pe;
while pARMA==0
if SA1(i,i)>=0.01
pARMA=i;
else
i=i-2;
end
end
%计算Sp
SpARMA=zeros(pARMA+1,pARMA+1);
for i=1:pARMA
for k=1:(pe-pARMA+1)
SpARMA=SpARMA+SA(i,i)*VA(k:k+pARMA,i)*(VA(k:k+pARMA,i))';
end
end
%AR参数的估计值为:
SpnARMA=SpARMA^(-1);
aARMA=SpnARMA(:,1)/SpnARMA(1,1);
rARMA=roots(aARMA);
fARMA=atan(abs(imag(rARMA)./real(rARMA)))/(2*pi)
%MUSIC方法实现谐波恢复
%以下求观测数据相关函数矩阵
RMUSIC=rot90(hankel(R((2*N-1):-1:N),R(N:-1:1)));
[XMUSIC,DMUSIC]=eig(RMUSIC);
%以下寻找谐波个数
pm=0;%谐波个数
k=1;
while pm==0
if (DMUSIC(k,k)-DMUSIC(k+1,k+1))/DMUSIC(k+1,k+1)>=1.2
pm=k;
else
k=k+1;
end
end
display('谐波个数为:')
pm=4
S=XMUSIC(:,1:pm);
SHconj=S';
Ps=S*SHconj;
NMUSIC=256;%分段数量
wiMUSIC=2*pi/NMUSIC;%频率搜索步长
ww=1:NMUSIC;
f=ww/NMUSIC;%频率向量
%以下构造A矩阵
NN=t'*ww;
awi=exp(j*wiMUSIC*NN);
awic=awi';
fMUSIC=0;
PWxMUSIC=zeros(1,NMUSIC);
for k=1:NMUSIC
PWxMUSIC(k)=1/(awic(k,:)*(eye(N,N)-Ps)*awi(:,k));
%搜索极大值
if k>=2&&k<NMUSIC/2
if PWxMUSIC(k)>fMUSIC
fMUSIC=k/NMUSIC;
end
end
end
display('MUSIC方法估计的频率:')
fMUSIC
figure(1);
stem(f,abs(PWxMUSIC),'filled');
title('MUSIC方法得到的谱');
xlabel('f');
ylabel('PMUSIC');
%ESPRIT方法实现谐波恢复
%第一步构造自相关矩阵Rxx和Rxy
mESPRIT=4;
Rxx=rot90(hankel(R(N+mESPRIT-1:-1:N),conj(R(N:N+mESPRIT-1))));
Rxy=rot90(hankel(R(N-mESPRIT:N-1),R(N-1:N+mESPRIT-2)),3);
[XESPRIT,DESPRIT]=eig(Rxx);
Q2ESPRIT=min(diag(DESPRIT));
Cxx=Rxx-Q2ESPRIT*eye(size(Rxx));
Cxy=Rxy-Q2ESPRIT*diag(ones(1,mESPRIT-1),-1);
%LS-ESPRIT算法
[XESPRIT,DESPRIT]=eig(Cxx,Cxy);
display('LS-ESPRIT方法估计的频率:')
fESPRIT_LS=atan(abs(imag(diag(DESPRIT))./real(diag(DESPRIT))))/(2*pi)
%TLS-ESPRIT算法
[UESPRIT,SESPRIT,VESPRIT]=svd(Cxx);
%奇异值归一化,并确定有效秩p
SESPRIT1=SESPRIT/SESPRIT(1,1);
pESPRIT=0;
k=mESPRIT;
while pESPRIT==0
if abs(SESPRIT1(k,k))>=0.002
pESPRIT=k;
else
k=k-1;
end
end
UESPRITp=UESPRIT(:,1:pESPRIT);
SESPRITp=SESPRIT(1:pESPRIT,1:pESPRIT);
VESPRITp=VESPRIT(:,1:pESPRIT);
Cxyp=UESPRITp'*Cxy*VESPRITp;
[XESPRITp,DESPRITp]=eig(SESPRITp,Cxyp);
display('TLS-ESPRIT方法估计的频率:')
fESPRIT_TLS=atan(abs(imag(diag(DESPRITp))./real(diag(DESPRITp))))/(2*pi)
