课程名称：  数字逻辑电路与系统    

     院    系：  电子与信息工程学院   

     班    级：      1205102           

     姓    名：                  

     学    号：       1120510      

     教    师：        吴芝路           

哈尔滨工业大学

20##年12月

实验二时序逻辑电路的设计与仿真

3.1 实验要求

本实验练习在Maxplus II环境下时序逻辑电路的设计与仿真，共包括6个子实验，要求如下：

3.2 同步计数器实验

3.2.1 实验目的

1. 练习使用计数器设计简单的时序电路

2. 熟悉用MAXPLUS II仿真时序电路的方法

3.2.2 实验预习要求

1. 预习教材《6-3 计数器》

2. 了解本次实验的目的、电路设计要求

3.2.3 实验原理

计数器是最基本、最常用的时序逻辑电路之一，有很多品种。按计数后的输出数码来分，有二进制及BCD码等区别；按计数操作是否有公共外时钟控制来分，可分为异步及同步两类；此外，还有计数器的初始状态可否预置，计数长度（模）可否改变，以及可否双向等区别。

本实验用集成同步4位二进制加法计数器74LS161设计N分频电路，使输出信号CPO的频率为输入时钟信号CP频率的1/N，其中N=(学号后两位mod 8)+8。下表为74LS161的功能表。

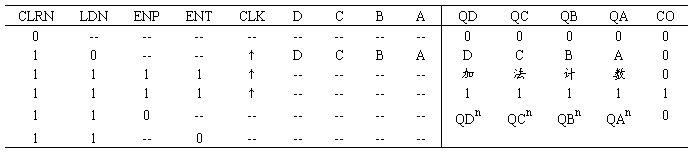
3.2.4 实验步骤

1. 打开MAXPLUS II, 新建一个原理图文件，命名为EXP3_2.gdf。

2. 按照实验要求设计电路，将电路原理图填入下表。

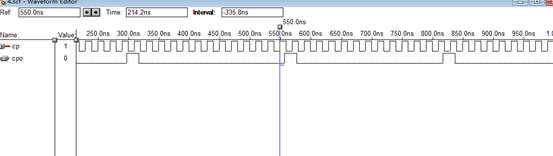
3. 新建一个波形仿真文件，命名为EXP3_2.scf，加入时钟输入信号CP及输出信号CPO，并点击MAXPLUS II左侧工具条上的时钟按钮，将CP的波形设置为周期性方波。

4. 运行仿真器得到输出信号CPO的波形，将完整的仿真波形图（包括全部输入输出信号）附于下表。

3.3 时序电路分析实验

3.3.1 实验目的

练习用 MAXPLUS II 进行时序逻辑电路的分析。

3.3.2 实验预习要求

1.  预习教材《6-3-1 异步二进制计数器》

2.  了解本次实验的目的、电路分析要求

3.3.3 实验原理

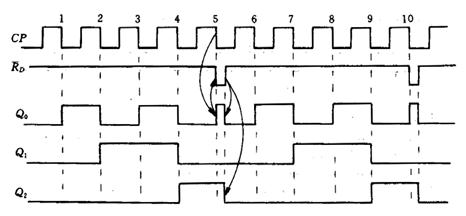
分析如下时序电路的功能，并判断给出的波形图是否正确。

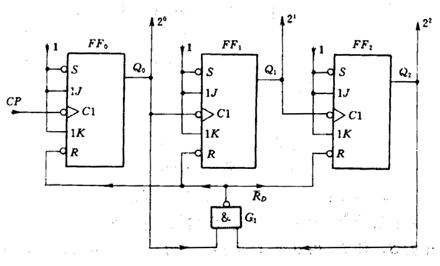
3.3.4 实验原理

  1.打开 MAXPLUS II,  新建一个原理图文件，命名为 EXP3_3.gdf。

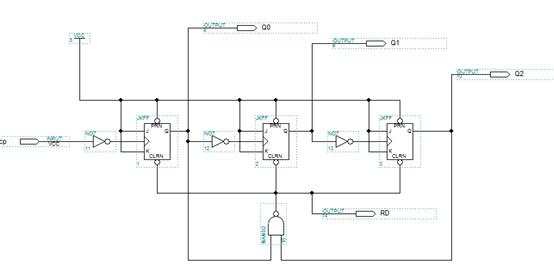
2.将给出的电路图输入 MAXPLUS II 的原理图中，其中 JK 触发器在 MAXPLUSII 中的符号位 JKFF。

3.新建一个波形仿真文件，命名为 EXP3_3.scf，加入所有输入输出信号，并按照给出的波形图绘制输入信号 CP、 RD的波形。

 4.运行仿真器得到输出信号 Q0 , Q1 , Q2 的波形，将完整的仿真波形图（包括全部输入输出信号）附于下表。

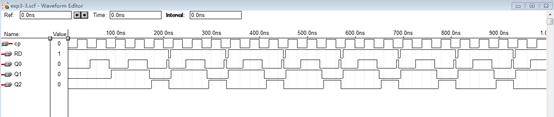
5.  对比实验原理中给出的波形与 MAXPLUS II 仿真得出的波形，指出两者的异同，并分析原因。

  答：可以发现实验仿真图和书本上的不一样，主要体现在归零信号产生之。

因为当归零信号到来的时候，第二个触发器会被清零，第一个触发器由于有延迟，使得输出延迟，从而开始的“1”输出将被清零后的第二个触发器获得，从而最后结果为2。

3.4移位寄存器实验

3.4.1 实验目的

练习使用移位寄存器设计简单的时序电路。

3.4.2 实验预习要求

1. 预习教材《6-4 移位寄存器》

2. 了解本次实验的目的、电路设计要求

3.4.3 实验原理

数据的移位寄存是一种常见的算数和逻辑动作，例如在进行算数的乘法或除法过程中，就需要将部分积进行先移位，再相加或相减的操作。移位寄存器从结构上看，是将若干个触发器级联起来，按数据输入方式来分，有串行和并行两种，而移位方向则有左移和右移之区别，同时数据输出也有并出和串出之分。

请用4位双向通用移存器74LS194设计一个序列检测器，功能为：在时钟CP的驱动下，数据输入端D每个时钟周期输入1 bit二进制数，形成一个二进制序列，当序列中出现’1011’时，输出端F输出一个时钟周期的高电平，否则为低电平。

3.4.4 实验步骤

1. 打开MAXPLUS II, 新建一个原理图文件，命名为EXP3_4.gdf。

2. 按照实验要求设计电路，将电路原理图填入下表。

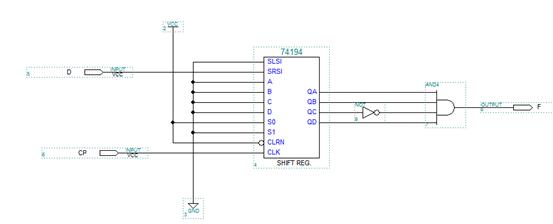
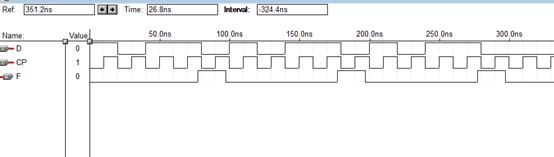
3. 新建一个波形仿真文件，命名为EXP3_4.scf，加入所有输入输出信号，并绘制输入信号CP、D的波形。

4. 运行仿真器得到输出信号F的波形，将完整的仿真波形图（包括全部输入输出信号）附于下表。

3.5 三人抢答器实验

3.5.1 实验目的

练习使用触发器设计简单的时序电路。

3.5.2 实验预习要求

1. 预习教材《第五章 触发器》

2. 了解本次实验的目的、电路设计要求

3.5.3 实验原理

设计一个如下图所示的抢答器。

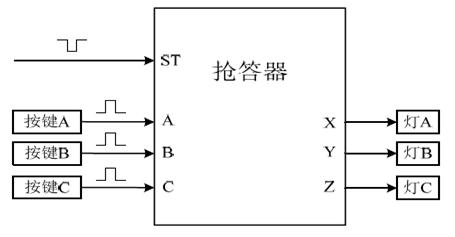
其中A、B、C 为三个抢答按键，ST 为起始信号，X、Y、Z 分别为A、B、

C 对应的输出。在ST 的一个负脉冲后，ABC 中最先按下（由’0’变为’1’）的按

键对应的输出端变为有效（由’0’变为’1’），其它输出端不变。

3.5.4 实验步骤

1. 打开MAXPLUS II, 新建一个原理图文件，命名为EXP3_5.gdf。

2. 按照实验要求设计电路，将电路原理图填入下表。

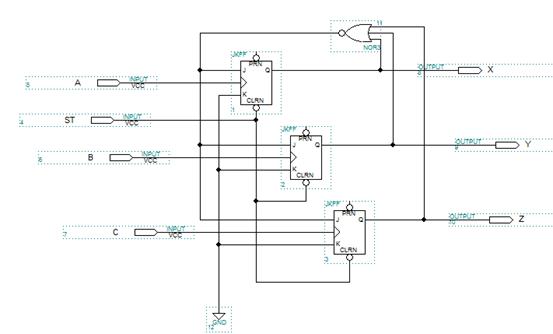
3. 新建一个波形仿真文件，命名为EXP3_5.scf，加入所有输入输出信号，并绘

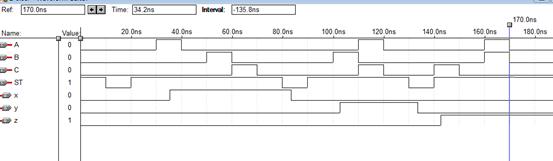
制输入信号ST、A、B、C 的波形。

4. 运行仿真器得到输出信号X、Y、Z 的波形，将完整的仿真波形图（包括全部

输入输出信号）附于下表。

心得体会：

经过这次实验，我对第六章的内容有了更深刻的理解，在实验中一点小错误就会导致最终结果的极大偏差，当结果出错时，往往都是课本知识使自己快速找到错误，也坚定了进一步学号数电理论知识的决心。

第二篇：哈工大-数值分析上机实验报告

实验报告一

题目： 非线性方程求解

摘要：非线性方程的解析解通常很难给出，因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。

前言：（目的和意义）

掌握二分法与Newton法的基本原理和应用。

数学原理：

对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法：二分法和Newton法。

对于二分法，其数学实质就是说对于给定的待求解的方程f(x)，其在[a,b]上连续，f(a)f(b)<0，且f(x)在[a,b]内仅有一个实根x*，取区间中点c，若，则c恰为其根，否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个，从而得出新区间，仍称为[a,b]。重复运行计算，直至满足精度为止。这就是二分法的计算思想。

Newton法通常预先要给出一个猜测初值x0，然后根据其迭代公式

xk?1?xk?f(xk) 'f(xk)

产生逼近解x*的迭代数列{xk}，这就是Newton法的思想。当x0接近x*时收敛很快，但是当x0选择不好时，可能会发散，因此初值的选取很重要。另外，若将该迭代公式改进为

xk?1?xk?rf(xk) f'(xk)

其中r为要求的方程的根的重数，这就是改进的Newton法，当求解已知重数的方程的根时，在同种条件下其收敛速度要比Newton法快的多。

程序设计：

本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式，如下

function y=f(x);

y=-x*x-sin(x);

写成如上形式即可，下面给出主程序。

二分法源程序：

clear

.1.

%%%给定求解区间

b=1.5;

a=0;

%%%误差

R=1;

k=0;%迭代次数初值

while (R>5e-6) ;

c=(a+b)/2;

if f12(a)*f12(c)>0;

a=c;

else

b=c;

end

R=b-a;%求出误差

k=k+1;

end

x=c%给出解

Newton法及改进的Newton法源程序：

clear

%%%% 输入函数

f=input('请输入需要求解函数>>','s')

%%%求解f(x)的导数

df=diff(f);

%%%改进常数或重根数

miu=2;

%%%初始值x0

x0=input('input initial value x0>>');

k=0;%迭代次数

max=100;%最大迭代次数

R=eval(subs(f,'x0','x'));%求解f(x0)，以确定初值x0时否就是解 while (abs(R)>1e-8)

x1=x0-miu*eval(subs(f,'x0','x'))/eval(subs(df,'x0','x')); R=x1-x0;

x0=x1;

k=k+1;

if (eval(subs(f,'x0','x'))<1e-10);

.2.

break

end

if k>max;%如果迭代次数大于给定值，认为迭代不收敛，重新输入初值 ss=input('maybe result is error,choose a new x0,y/n?>>','s');

if strcmp(ss,'y')

x0=input('input initial value x0>>');

k=0;

else

break

end

end

end

k;%给出迭代次数

x=x0；%给出解

结果分析和讨论：

x2

?0在[1，2]内的根。(??5*10?6,下同) 1. 用二分法计算方程sinx?2

计算结果为

x= 1.40441513061523；

f(x)= -3.797205105904311e-007；

k=18；

由f(x)知结果满足要求，但迭代次数比较多，方法收敛速度比较慢。

2. 用二分法计算方程x3?x?1?0在[1，1.5]内的根。

计算结果为

x= 1.32471847534180；

f(x)= 2.209494846194815e-006；

k=17；

由f(x)知结果满足要求，但迭代次数还是比较多。

3. 用Newton法求解下列方程

a) xex?1?0 x0=0.5；

计算结果为

x= 0.56714329040978；

f(x)= 2.220446049250313e-016；

k=4；

由f(x)知结果满足要求，而且又迭代次数只有4次看出收敛速度很快。

.3.

b) x3?x?1?0 x0=1；

c) (x?1)2(2x?1)?0 x0=0.45, x0=0.65；

当x0=0.45时，计算结果为

x= 0.49999999999983；

f(x)= -8.362754932994584e-014；

k=4；

由f(x)知结果满足要求，而且又迭代次数只有4次看出收敛速度很快，实际上该方程确实有真解x=0.5。

当x0=0.65时，计算结果为

x= 0.50000000000000；

f(x)=0；

k=9；

由f(x)知结果满足要求，实际上该方程确实有真解x=0.5，但迭代次数增多，实际上当取x0〉0.68时，x≈1，就变成了方程的另一个解，这说明Newton法收敛与初值很有关系，有的时候甚至可能不收敛。

4. 用改进的Newton法求解，有2重根，取??2

(x?1)2(2x?1)?0 x0=0.55；并与3.中的c)比较结果。

当x0=0.55时，程序死循环，无法计算，也就是说不收敛。改??1.5时，结果收敛为

x=0.50000087704286；

f(x)=4.385198907621127e-007；

k=16；

显然这个结果不是很好，而且也不是收敛至方程的2重根上。

当x0=0.85时，结果收敛为

x= 1.00000000000489；

f(x)= 2.394337647718737e-023；

k=4；

这次达到了预期的结果，这说明初值的选取很重要，直接关系到方法的收敛性，实际上直接用Newton法，在给定同样的条件和精度要求下，可得其迭代次数k=15，这说明改进后的Newton法法速度确实比较快。

结论：

对于二分法，只要能够保证在给定的区间内有根，使能够收敛的，当时收敛的速度和给定的区间有关，二且总体上来说速度比较慢。Newton法，收敛速度要比二分法快，但是最终其收敛的结果与初值的选取有关，初值不同，收敛的结果也可能不一样，也就是结果可能不时预期需要得结果。改进的Newton法求解重根问题时，如果初值不当，可能会不收敛，这一点非常重要，当然初值合适，相同情况下其速度要比Newton法快得多。

.4.

实验报告二

题目： Gauss列主元消去法

摘要：求解线性方程组的方法很多，主要分为直接法和间接法。本实验运用直接法的Guass消去法,并采用选主元的方法对方程组进行求解。

前言：（目的和意义）

1. 学习Gauss消去法的原理。

2. 了解列主元的意义。 3. 确定什么时候系数阵要选主元

数学原理：

(k?1)由于一般线性方程在使用Gauss消去法求解时，从求解的过程中可以看到，若akk=0，

(k?1)则必须进行行交换，才能使消去过程进行下去。有的时候即使akk?0，但是其绝对值非

常小，由于机器舍入误差的影响，消去过程也会出现不稳定得现象，导致结果不正确。因此有必要进行列主元技术，以最大可能的消除这种现象。这一技术要寻找行r，使得

(k?1)(k?1)|ark|?maxaik i?k

(k?1)并将第r行和第k行的元素进行交换，以使得当前的akk的数值比0要大的多。这种列主

元的消去法的主要步骤如下：

1. 消元过程

对k=1,2,…,n-1,进行如下步骤。

1) 选主元，记

|ark|?aik i?k

若|ark|很小，这说明方程的系数矩阵严重病态，给出警告，提示结果可能不对。

2) 交换增广阵A的r，k两行的元素。

arj?akj (j=k,…,n+1)

3) 计算消元

aij?aij?aikakj/akk (i=k+1,…,n; j=k+1,……,n+1)

2. 回代过程

对k= n, n-1,…,1,进行如下计算

.5.

xk?(ak,n?1?

至此，完成了整个方程组的求解。

程序设计：

本实验采用Matlab的M文件编写。

Gauss消去法源程序：

clear

a=input('输入系数阵：>>\n')

b=input('输入列阵b：>>\n')

n=length(b);

A=[a b]

x=zeros(n,1);

%%%函数主体

for k=1:n-1;

%%%是否进行主元选取 j?k?1?ankjxj/akk)

if abs(A(k,k))<yipusilong;%事先给定的认为有必要选主元的小数

yzhuyuan=1;

else yzhuyuan=0;

end

if yzhuyuan;

%%%%选主元

t=A(k,k);

for r=k+1:n;

if abs(A(r,k))>abs(t)

p=r;

else p=k;

end

end

%%%交换元素

if p~=k;

for q=k:n+1;

s=A(k,q);

A(k,q)=A(p,q);

A(p,q)=s;

end

.6.

end

end

%%%判断系数矩阵是否奇异或病态非常严重

if abs(A(k,k))< yipusilong

disp(‘矩阵奇异，解可能不正确’)

end

%%%%计算消元,得三角阵

for r=k+1:n;

m=A(r,k)/A(k,k);

for q=k:n+1;

A(r,q)=A(r,q)-A(k,q)*m;

end

end

end

%%%%求解x

x(n)=A(n,n+1)/A(n,n);

for k=n-1:-1:1;

s=0;

for r=k+1:n;

s=s+A(k,r)*x(r);

end

t=(A(k,n+1)-s)

x(k)=(A(k,n+1)-s)/A(k,k)

end

结果分析和讨论：

??26??x??22???y???34?。其中为一小数，当?5?10?14?20575例：求解方程?时，??10,10,10,10?????????321????z????10??

分别采用列主元和不列主元的Gauss消去法求解，并比较结果。

记Emax为求出的解代入方程后的最大误差，按要求，计算结果如下：

当??10?5时，不选主元和选主元的计算结果如下，其中前一列为不选主元结果，后一列为选主元结果，下同。

0.99999934768391 0.99999934782651

2.00000217421972 2.00000217391163

2.99999760859451 2.99999760869721

.7.

Emax= 9.301857062382624e-010，0

此时，由于?不是很小，机器误差就不是很大，由Emax可以看出不选主元的计算结果精度还可以，因此此时可以考虑不选主元以减少计算量。

当??10?10时，不选主元和选主元的计算结果如下

1.00001784630877 0.99999999999348

1.99998009720807 2.00000000002174

3.00000663424731 2.99999999997609

Emax= 2.036758973744668e-005，0

此时由Emax可以看出不选主元的计算精度就不好了，误差开始增大。

当??10?14时，不选主元和选主元的计算结果如下

1.42108547152020 1.00000000000000

1.66666666666666 2.00000000000000

3.11111111111111 300000000000000

Emax= 0.70770085900503，0

此时由Emax可以看出，不选主元的结果应该可以说是不正确了，这是由机器误差引起的。

当??10?20时，不选主元和选主元的计算结果如下

NaN 1

NaN 2

NaN 3

Emax=NaN, 0

不选主元时，程序报错：Warning: Divide by zero.。这是因为机器计算的最小精度为10-15，所以此时的??10?20就认为是0，故出现了错误现象。而选主元时则没有这种现象，而且由Emax可以看出选主元时的结果应该是精确解。

结论：

采用Gauss消去法时，如果在消元时对角线上的元素始终较大（假如大于10-5），那么本方法不需要进行列主元计算，计算结果一般就可以达到要求，否则必须进行列主元这一步，以减少机器误差带来的影响，使方法得出的结果正确。

.8.

实验报告三

题目： Rung现象产生和克服

摘要：由于高次多项式插值不收敛，会产生Runge现象，本实验在给出具体的实例后，采用分段线性插值和三次样条插值的方法有效的克服了这一现象，而且还取的很好的插值效果。

前言：（目的和意义）

1. 深刻认识多项式插值的缺点。

2. 明确插值的不收敛性怎样克服。

3. 明确精度与节点和插值方法的关系。

数学原理：

在给定n+1个节点和相应的函数值以后构造n次的Lagrange插值多项式，实验结果表明（见后面的图）这种多项式并不是随着次数的升高对函数的逼近越来越好，这种现象就是Rung现象。

解决Rung现象的方法通常有分段线性插值、三次样条插值等方法。

分段线性插值：

设在区间[a, b]上，给定n+1个插值节点

a=x0<x1<…<xn=b

和相应的函数值y0，y1，…，yn，，求作一个插值函数?(x)，具有如下性质：

1) ?(xj)?yj，j=0，1，…，n。

2) ?(x)在每个区间[xi, xj]上是线性连续函数。则插值函数?(x)称为区间[a, b]上对应n个数据点的分段线性插值函数。

三次样条插值：

给定区间[a, b]一个分划

⊿：a=x0<x1<…<xN=b

若函数S(x)满足下列条件：

1) S(x)在每个区间[xi, xj]上是不高于3次的多项式。

2) S(x)及其2阶导数在[a, b]上连续。则称S(x)使关于分划⊿的三次样条函数。

程序设计：

本实验采用Matlab的M文件编写。其中待插值的方程写成function的方式，如下

function y=f(x);

.9.

y=1/（1+25*x*x）;

写成如上形式即可，下面给出主程序

Lagrange插值源程序：

n=input('将区间分为的等份数输入：\n');

s=[-1+2/n*[0:n]];%%%给定的定点，Rf为给定的函数 x=-1:0.01:1;

f=0;

for q=1:n+1;

l=1;%求插值基函数

for k=1:n+1;

if k~=q;

l=l.*(x-s(k))./(s(q)-s(k));

else

l=l;

end

end

f=f+Rf(s(q))*l;%求插值函数

end

plot(x,f,'r')%作出插值函数曲线

grid on

hold on

分段线性插值源程序

clear

n=input('将区间分为的等份数输入：\n');

s=[-1+2/n*[0:n]];%%%给定的定点，Rf为给定的函数 m=0;

hh=0.001;

for x=-1:hh:1;

ff=0;

for k=1:n+1;%%%求插值基函数

switch k

case 1

if x<=s(2);

l=(x-s(2))./(s(1)-s(2));

else

l=0;

.10.

end

case n+1

if x>s(n);

l=(x-s(n))./(s(n+1)-s(n));

else

l=0;

end

otherwise

if x>=s(k-1)&x<=s(k);

l=(x-s(k-1))./(s(k)-s(k-1));

else if x>=s(k)&x<=s(k+1);

l=(x-s(k+1))./(s(k)-s(k+1));

else

l=0;

end

end

end

ff=ff+Rf(s(k))*l;%%求插值函数值

end

m=m+1;

f(m)=ff;

end

%%%作出曲线

x=-1:hh:1;

plot(x,f,'r');

grid on

hold on

三次样条插值源程序：（采用第一边界条件）

clear

n=input('将区间分为的等份数输入：\n');

%%%插值区间

a=-1;

b=1;

hh=0.001;%画图的步长

s=[a+(b-a)/n*[0:n]];%%%给定的定点，Rf为给定的函数 %%%%第一边界条件Rf"(-1),Rf"(1)

.11.

v=5000*1/(1+25*a*a)^3-50/(1+25*a*a)^4;

for k=1:n;%取出节点间距

h(k)=s(k+1)-s(k);

end

for k=1:n-1;%求出系数向量lamuda,miu

la(k)=h(k+1)/(h(k+1)+h(k));

miu(k)=1-la(k);

end

%%%%赋值系数矩阵A

for k=1:n-1;

for p=1:n-1;

switch p

case k

A(k,p)=2;

case k-1

A(k,p)=miu(p+1);

case k+1

A(k,p)=la(p-1);

otherwise

A(k,p)=0;

end

end

end

%%%%求出d阵

for k=1:n-1;

switch k

case 1

d(k)=6*f2c([s(k) s(k+1) s(k+2)])-miu(k)*v; case n-1

d(k)=6*f2c([s(k) s(k+1) s(k+2)])-la(k)*v; otherwise

d(k)=6*f2c([s(k) s(k+1) s(k+2)]);

end

end

%%%%求解M阵

M=A\d';

.12.

M=[v;M;v];

%%%%

m=0;

f=0;

for x=a:hh:b;

if x==a;

p=1;

else

p=ceil((x-s(1))/((b-a)/n));

end

ff1=0;

ff2=0;

ff3=0;

ff4=0;

m=m+1;

ff1=1/h(p)*(s(p+1)-x)^3*M(p)/6;

ff2=1/h(p)*(x-s(p))^3*M(p+1)/6;

ff3=((Rf(s(p+1))-Rf(s(p)))/h(p)-h(p)*(M(p+1)-M(p))/6)*(x-s(p));

ff4=Rf(s(p))-M(p)*h(p)*h(p)/6;

f(m)=ff1+ff2+ff3+ff4 ;

end

%%%作出插值图形

x=a:hh:b;

plot(x,f,'k')

hold on

grid on

结果分析和讨论：

本实验采用函数f(x)?1进行数值插值，插值区间为[-1，1]，给定节点为 21?25x

xj=-1+jh,h=0.1，j=0,…，n。下面分别给出Lagrange插值，三次样条插值，线性插值的函数曲线和数据表。图中只标出Lagrange插值的十次多项式的曲线，其它曲线没有标出，从数据表中可以看出具体的误差。

.13.

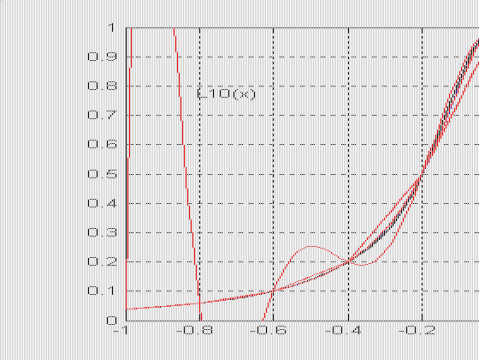
表中，L10(x)为Lagrange插值的10次多项式，S10(x)，S40(x)分别代表n=10，40的三次样条插值函数，X10(x)，X40(x)分别代表n=10，40的线性分段插值函数。

x f(x) L10(x) S10(x) S40(x) X10(x) X40(x) -1.00000000000000 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 -0.95000000000000 0.04244031830239 1.92363114971920 0.04240833151040 0.04244031830239 0.04355203619910 0.04244031830239 -0.90000000000000 0.04705882352941 1.57872099034926 0.04709697585458 0.04705882352941 0.04864253393665 0.04705882352941 -0.85000000000000 0.05245901639344 0.71945912837982 0.05255839923979 0.05245901639344 0.05373303167421 0.05245901639344 -0.80000000000000 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 -0.75000000000000 0.06639004149378 -0.23146174989674 0.06603986172744 0.06639004149378 0.06911764705882 0.06639004149378 -0.70000000000000 0.07547169811321 -0.22619628906250 0.07482116198866 0.07547169811321 0.07941176470588 0.07547169811321 -0.65000000000000 0.08648648648649 -0.07260420322418 0.08589776360849 0.08648648648649 0.08970588235294 0.08648648648649 -0.60000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 -0.55000000000000 0.11678832116788 0.21559187891257 0.11783833017713 0.11678832116788 0.12500000000000 0.11678832116788 -0.50000000000000 0.13793103448276 0.25375545726103 0.14004371555730 0.13793103448276 0.15000000000000 0.13793103448276 -0.45000000000000 0.16494845360825 0.23496854305267 0.16722724315883 0.16494845360825 0.17500000000000 0.16494845360825 -0.40000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 -0.35000000000000 0.24615384615385 0.19058046675376 0.24054799403464 0.24615384615385 0.27500000000000 0.24615384615385 -0.30000000000000 0.30769230769231 0.23534659131080 0.29735691695860 0.30769230769231 0.35000000000000 0.30769230769231 -0.25000000000000 0.39024390243902 0.34264123439789 0.38048738140327 0.39024390243902 0.42500000000000 0.39024390243902 -0.20000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 -0.15000000000000 0.64000000000000 0.67898957729340 0.65746969368431 0.64000000000000 0.62500000000000 0.64000000000000 -0.10000000000000 0.80000000000000 0.84340742982890 0.82052861660828 0.80000000000000 0.75000000000000 0.80000000000000 -0.05000000000000 0.94117647058824 0.95862704866073 0.94832323122810 0.94117647058824 0.87500000000000 0.94117647058824 0 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 1.00000000000000 0.05000000000000 0.94117647058824 0.95862704866073 0.94832323122810 0.94117647058824 0.87500000000000 0.94117647058824 0.10000000000000 0.80000000000000 0.84340742982890 0.82052861660828 0.80000000000000 0.75000000000000 0.80000000000000 0.15000000000000 0.64000000000000 0.67898957729340 0.65746969368431 0.64000000000000 0.62500000000000 0.64000000000000 0.20000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.50000000000000 0.25000000000000 0.39024390243902 0.34264123439789 0.38048738140327 0.39024390243902 0.42500000000000 0.39024390243902 0.30000000000000 0.30769230769231 0.23534659131080 0.29735691695860 0.30769230769231 0.35000000000000 0.30769230769231 0.35000000000000 0.24615384615385 0.19058046675376 0.24054799403464 0.24615384615385 0.27500000000000 0.24615384615385 0.40000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.20000000000000 0.45000000000000 0.16494845360825 0.23496854305267 0.16722724315883 0.16494845360825 0.17500000000000 0.16494845360825 0.50000000000000 0.13793103448276 0.25375545726103 0.14004371555730 0.13793103448276 0.15000000000000 0.13793103448276

.14.

0.60000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.10000000000000 0.65000000000000 0.08648648648649 -0.07260420322418 0.08589776360849 0.08648648648649 0.08970588235294 0.08648648648649 0.70000000000000 0.07547169811321 -0.22619628906250 0.07482116198866 0.07547169811321 0.07941176470588 0.07547169811321 0.75000000000000 0.06639004149378 -0.23146174989674 0.06603986172744 0.06639004149378 0.06911764705882 0.06639004149378 0.80000000000000 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.05882352941176 0.85000000000000 0.05245901639344 0.71945912837982 0.05255839923979 0.05245901639344 0.05373303167421 0.05245901639344 0.90000000000000 0.04705882352941 1.57872099034926 0.04709697585458 0.04705882352941 0.04864253393665 0.04705882352941 0.95000000000000 0.04244031830239 1.92363114971920 0.04240833151040 0.04244031830239 0.04355203619910 0.04244031830239 1.00000000000000 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154 0.03846153846154

从以上结果可以看到，用三次样条插值和线性分段插值，不会出现多项式插值是出现的Runge现象，插值效果明显提高。进一步说，为了提高插值精度，用三次样条插值和线性分段插值是可以增加插值节点的办法来满足要求，而用多项式插值函数时，节点数的增加必然会使多项式的次数增加，这样会引起数值不稳定，所以说这两种插值要比多项式插值好的多。而且在给定节点数的条件下，三次样条插值的精度要优于线性分段插值，曲线的光滑性也要好一些。

.15.

实验报告四

题目： 多项式最小二乘法

摘要：对于具体实验时，通常不是先给出函数的解析式，再进行实验，而是通过实验的观察和测量给出离散的一些点，再来求出具体的函数解析式。又因为测量误差的存在，实际真实的解析式曲线并不一定通过测量给出的所有点。最小二乘法是求解这一问题的很好的方法，本实验运用这一方法实现对给定数据的拟合。

前言：（目的和意义）

1. 学习使用最小二成法的原理

2. 了解法方程的特性

数学原理：

对于给定的测量数据(xi,fi)(i=1,2,…，n)，设函数分布为

m

y(x)??aj?j(x)

j?0

特别的，取?j(x)为多项式

?j(x)?xj (j=0, 1,…，m)

则根据最小二乘法原理，可以构造泛函

H(a0,a1,?,am)??(fi??aj?j(xi))

i?1j?0nm

令

?H?0 (k=0, 1,…，m) ?ak

则可以得到法方程

?(?0,?0)(?1,?0)?(?m,?0)??a0??(f,?0)??(?,?)(?,?)?(?,?)??a??(f,?)?

11m1??1?1??01?? ?????????????????(?,?)(?,?)?(?,?)a(f,?)1mmm??m?m??0m?

求该解方程组，则可以得到解a0,a1,?,am，因此可得到数据的最小二乘解

f(x)??aj?j(x)

j?0m

.16.

程序设计：

本实验采用Matlab的M文件编写。其中多项式函数?j?xj写成function的方式，如下

function y=fai(x,j)

y=1;

for i=1:j

y=x.*y;

end

写成如上形式即可，下面给出主程序。

多项式最小二乘法源程序

clear

%%%给定测量数据点(s,f)

s=[3 4 5 6 7 8 9];

f=[2.01 2.98 3.50 5.02 5.47 6.02 7.05];

%%%计算给定的数据点的数目

n=length(f);

%%%给定需要拟合的数据的最高次多项式的次数 m=10;

%%%程序主体

for k=0:m;

g=zeros(1,m+1);

for j=0:m;

t=0;

for i=1:n;%计算内积(fai(si),fai(si))

t=t+fai(s(i),j)*fai(s(i),k);

end

g(j+1)=t;

end

A(k+1,:)=g;%法方程的系数矩阵

t=0;

for i=1:n;%计算内积(f(si),fai(si))

t=t+f(i)*fai(s(i),k);

end

b(k+1,1)=t;

end

.17.

a=A\b%求出多项式系数

x=[s(1):0.01:s(n)]';

y=0;

for i=0:m;

y=y+a(i+1)*fai(x,i);

end

plot(x,y)%作出拟合成的多项式的曲线

grid on

hold on

plot(s,f,'rx') %在上图中标记给定的点

结果分析和讨论：

例 用最小二乘法处理下面的实验数据.

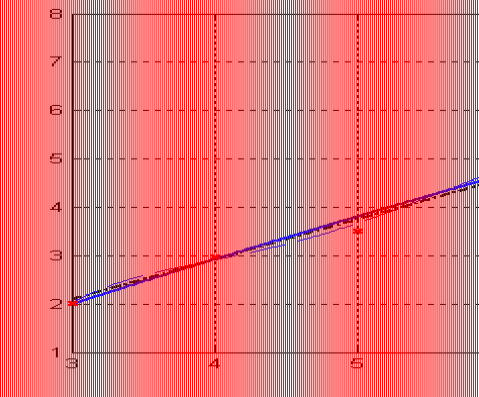
并作出f(x)的近似分布图。

分别采用一次，二次和五次多项式来拟合数据得到相应的拟合多项式为：

y1=-0.38643+0.82750x；

y2=-1.03024+1.06893x-0.02012x2；

y5=-50.75309+51.53527x-19.65947x2+3.66585x3-0.32886x4+0.01137x5；

分别作出它们的曲线图，图中点划线为y1曲线，实线为y2曲线，虚线为y5曲线。’x’为给定的数据点。从图中可以看出并不是多项式次数越高越好，次数高了，曲线越能给定点处和实际吻合，但别的地方就很差了。因此，本例选用一次和两次的多项式拟合应该就可以了。

.18.

实验报告五

题目： Romberg积分法

摘要：对于实际的工程积分问题，很难应用Newton-Leibnitz公式去求解。因此应用数值方法进行求解积分问题已经有着很广泛的应用，本文基于Romberg积分法来解决一类积分问题。

前言：（目的和意义）

1. 理解和掌握Romberg积分法的原理；

2. 学会使用Romberg积分法；

3. 明确Romberg积分法的收敛速度及应用时容易出现的问题。

数学原理：

考虑积分I(f)??f(x)dx，欲求其近似值，通常有复化的梯形公式、Simpsion公式和ab

Cotes公式。但是给定一个精度，这些公式达到要求的速度很缓慢。如何提高收敛速度，自然是人们极为关心的课题。为此，记T1,k为将区间[a,b]进行2k等分的复化的梯形公式计算结果，记T2,k为将区间[a,b]进行2k等分的复化的Simpsion公式计算结果，记T3,k为将区间[a,b]进行2k等分的复化的Cotes公式计算结果。根据Richardson外推加速方法，可以得到收敛速度较快的Romberg积分法。其具体的计算公式为：

1. 准备初值，计算

T1,1?a?b[f(a)?f(b)] 2

k?12. 按梯形公式的递推关系，计算

T1,k?11b?a2?1b?a?T1,k?k?f(a?k?1(i?0.5)) 222i?04m?1Tm?1,k?1?m?Tm?1,k?m

4m?1?13. 按Romberg积分公式计算加速值 Tm,k?m? m=2,…，k

4. 精度控制。对给定的精度R，若

m,1?Tm?1,1?R

则终止计算，并取Tm,1为所求结果；否则返回2重复计算，直至满足要求的精度为止。

.19.

程序设计：

本实验采用Matlab的M文件编写。其中待积分的函数写成function的方式，例如如下

function yy=f(x,y);

yy=x.^3;

写成如上形式即可，下面给出主程序

Romberg积分法源程序

%%% Romberg积分法

clear

%%%积分区间

b=3;

a=1;

%%%精度要求

R=1e-5;

%%%应用梯形公式准备初值

T(1,1)=(b-a)*(f(b)+f(a))/2;

T(1,2)=T(1,1)/2+(b-a)/2*f((b+a)/2);

T(2,1)=(4*T(1,2)-T(1,1))/(4-1);

j=2;

m=2;

%%%主程序体%%%

while(abs(T(m,1)-T(m-1,1))>R);%%%精度控制

j=j+1;

s=0;

for p=1:2^(j-2);

s=s+f(a+(2*p-1)*h/(2^(j-1)));

end

T(1,j)=T(1,j-1)/2+h*s/(2^(j-1)); %%%梯形公式应用

for m=2:j;

k=(j-m+1);

T(m,k)=((4^(m-1))*T(m-1,k+1)-T(m-1,k))/(4^(m-1)-1);

end

end

%%%给出 Romberg积分法的函数表

I=T(m,1)

.20.

结果分析和讨论：

进行具体的积分时，精度取R=1e-8。

1. 求积分?100

6x3dx。精确解I= 24999676。

运行程序得Romberg积分法的函数表为

1.0e+007 *

4.70101520000000 3.05022950000000 2.63753307500000

2.49996760000000 2.49996760000000 0

2.49996760000000 0 0

由函数表知Romberg积分给出的结果为2.4999676*10^7，与精确没有误差，

精度很高。

2. 求积分?3

11dx。精确解I=ln3= 1.09861228866811。 x

运行程序得Romberg积分法的函数表为

1.33333333333333 1.16666666666667 1.11666666666667 1.10321067821068 1.09976770156303 1.09890151516846 1.09868461878559

1.11111111111111 1.10000000000000 1.09872534872535 1.09862004268048 1.09861278637027 1.09861231999130 0 1.09925925925926 1.09864037197371 1.09861302227749 1.09861230261625 1.09861228889937 0 0 1.09863054836600 1.09861258815533 1.09861229119306 1.09861228868164 0 0 0 1.09861251772313 1.09861229002850 1.09861228867179 0 0 0 0 1.09861228980593 1.09861228867046 0 0 0 0 0 1.09861228867019 0 0 0 0 0 0

从积分表中可以看出程序运行的结果为1.09861228867019，取8位有效数字，满足要求。

3. 求积分?sinxdx。 0x1

直接按前面方法进行积分，会发现系统报错，出现了0为除数的现象。出现这种情况的原因就是当x=0时，被积函数分母出现了0，如果用一个适当的小数?（最好不要小于程序给定的最小误差值，但是不能小于机器的最大精度）来代替，可以避免这个问题。本实验取??R，可得函数表为：

0.92073548319659 0.93979327500190 0.94451351171417 0.94569085359489 0.94598501993743

0.94614587227034 0.94608692395160 0.94608330088846 0.94608307538495 0

0.94608299406368 0.94608305935092 0.94608306035138 0 0

0.94608306038722 0.94608306036726 0 0 0

0.94608306036718 0 0 0 0

故该函数的积分为0.94608306036718，取8位有效数字。

4. 求积分?sinx2dx 01

本题的解析解很难给出，但运用Romberg积分可以很容易给出近似解，函数表为： 0.42073549240395 0.33406972582924 0.31597536075922 0.31168023948094 0.31062036680949 0.31035626065456

.21.

0.30518113697100 0.30994390573588 0.31024853238818 0.31026707591900 0.31026822526959 0

0.31026142365354 0.31026884083167 0.31026831215439 0.31026830189296 0 0

0.31026895856465 0.31026830376269 0.31026830173008 0 0 0

0.31026830119484 0.31026830172211 0 0 0 0

0.31026830172262 0 0 0 0 0

故该函数的积分为0.31026830172262，取8位有效数字。

结论：

Romberg积分通常要求被积函数在积分区间上没有奇点。如有奇点，且奇点为第一间断点，那么采用例3的方法，还是能够求出来的，否则，必须采用其它的积分方法。当然，Romberg积分的收敛速度还是比较快的。

.22.

实验报告六

题目： 常微分方程初值问题的数值解法

摘要：本实验主要采用经典四阶的R-K方法和四阶Adams预测-校正方法来求解常微分方程的数值解。

前言：（目的和意义）

通过编写程序，进行上机计算，使得对常微分方程初值问题的数值解法有更深刻的理解，掌握单步法和线性多步法是如何进行实际计算的及两类方法的适用范围和优缺点，特别是对这两类方法中最有代表性的方法:R-K方法和Adams方法及预测-校正方法有更好的理解。通过这两种方法的配合使用，掌握不同的方法如何配合在一起，解决实际问题。

数学原理：

对于一阶常微分方程初值问题

?dy/dx?f(x,y) （1） ??y(x0)?y0

的数值解法是近似计算中很中的一部分。

常微分方程的数值解法通常就是给出定义域上的n个等距节点，求出所对应的函数值yn。通常其数值解法可分为两大类：

1. 单步法：这类方法在计算yn+1的值时，只需要知道xn+1、xn和yn即可，就可算出。

这类方法典型有欧拉法和R-K法。

2. 多步法：这类方法在计算yn+1的值时，除了需要知道xn+1、xn和yn值外，还需要

知道前k步的值。典型的方法如Adams法。

经典的R-K法是一个四阶的方法。它最大的优点就是它是单步法，精度高，计算过程便于改变步长。其缺点也很明显，计算量大，每前进一步就要计算四次函数值f。它的具体的计算公式如式（2）所示。

四阶Adams预测-校正方法是一个线性多步法，它是由Adams显式公式

?yn?1?yn?(K1?2K2?2K3?K4)h/6?K1?f(xn,yn)??K2?f(xn?h/2,yn?K1h/2) （2） ??K3?f(xn?h/2,yn?K2h/2)??K4?f(xn?h,yn?K3h)?

和隐式公式组成，其计算公式如式（3）所示。

.23.

预测 n?1?yn?(55fn?59fn?1?37fn?2?9fn?3)h/24 （3a）

求导 n?1?f(xn?1,n?1) （3b）

校正 yn?1?yn?(9n?1?19fn?5fn?1?fn?2)h/24 （3c）

求导 fn?1?f(xn?1,yn?1) （3d）

将局部截断误差用预测值和校正值来表示，在预测和校正的公式中分别以它们各自的阶段误差来进行弥补，可期望的到精度更高的修正的预测-校正公式为：

预测 pn?1?yn?(55fn?59fn?1?37fn?2?9fn?3)h/24

修正 mn?1?pn?1?(cn?pn)251/270

求导 n?1?f(xn?1,mn?1)

校正 cn?1?yn?(9n?1?19fn?5fn?1?fn?2)h/24

修正 yn?1?cn?1?(cn?1?pn?1)19/270

求导 fn?1?f(xn?1,yn?1)

由于开始时无预测值和校正值可以利用，故令p0=c0=0，以后按上面进行计算。此方法的优点是可以减少计算量；缺点是它不是自开始的，需要先知道前面的四个点的值y0,y1,y2,y3，因此不能单独使用。另外，它也不便于改变步长。

程序设计：

本实验采用Matlab的M文件编写。其中待求的微分方程写成function的方式，如下

function yy=g(x,y);

yy=-x*x-y*y;

写成如上形式即可，下面给出主程序。

经典四阶的R-K方法源程序

clear

%%%步长选取

h=0.1;

%%%初始条件，即x=0时，y=1。

y(1)=1;

%%%求解区间

a=0;

b=2;

%%%迭代公式

for x=a:h:b-h;

k1=g(x,y((x-a)/h+1));%%g(x)?y'(x)，下同。

k2=g(x+h/2,y((x-a)/h+1)+h/2*k1);

k3=g(x+h/2,y((x-a)/h+1)+h/2*k2);

k4=g(x+h,y((x-a)/h+1)+h*k3);

y((x-a)/h+2)=y((x-a)/h+1)+h*(k1+2*k2+2*k3+k4)/6;

.24.

end

四阶Adams预测-校正方法源程序

%%%步长选取

h=0.1;

%%%初始条件

y(1)=1;

%%%求解区间

a=0;

b=2;

%%%应用RK迭代公式计算初始值y0,y1,y2,y3

for x=a:h:a+2*h;

k1=g(x,y((x-a)/h+1));

k2=g(x+h/2,y((x-a)/h+1)+h/2*k1);

k3=g(x+h/2,y((x-a)/h+1)+h/2*k2);

k4=g(x+h,y((x-a)/h+1)+h*k3);

y((x-a)/h+2)=y((x-a)/h+1)+h*(k1+2*k2+2*k3+k4)/6; end

%%%应用预测校正法求解

c(4)=0;%%%校正初值

p(4)=0;%%%预测初值

f(1)=g(a+0*h,y(1)); g(x)?y'(x)，且将该值存在数组f中。 f(2)=g(a+1*h,y(2));

f(3)=g(a+2*h,y(3));

f(4)=g(a+3*h,y(4));

for n=4:(b-a)/h;

%%%P预测

p(n+1)=y(n)+h/24*(55*f(n)-59*f(n-1)+37*f(n-2)-9*f(n-3)); %%%M修正

m(n+1)=p(n+1)+251/270*(c(n)-p(n));

%%%E求导

f(n+1)=g(a+(n+1-1)*h,m(n+1));

%%%C校正

c(n+1)=y(n)+h/24*(9*f(n+1)+19*f(n)-5*f(n-1)+f(n-2)); %%%M修正

y(n+1)=c(n+1)-19/270*(c(n+1)-p(n+1));

%%%E求导

.25.

f(n+1)=g(a+(n+1-1)*h,y(n+1));

end

结果分析和讨论：

?y'?x2?y2

计算实例一：对初值问题?取步长h=0.1;计算在[-1，0]上的数值解。

?y(?1)?0

在计算机上，运用所编的程序进行了运算，结果如下，其中第一列为在区间上的等分点，第二列为运用R-K法的计算结果，第三列为Adams预测-校正法计算结果。由于本题的解析解很难求出，无法看出精度如何，为此进行第二实例计算。

第一实例计算结果

-1.00000000000000 0 0

-0.90000000000000 0.09004735746240 0.09004735746240

-0.80000000000000 0.16072688390128 0.16072688390128

-0.70000000000000 0.21348265038268 0.21348265038268

-0.60000000000000 0.25036836954459 0.25036768670937

-0.50000000000000 0.27377524760451 0.27377644362732

-0.40000000000000 0.28622191831814 0.28622489850956

-0.30000000000000 0.29021334157377 0.29021772444822

-0.20000000000000 0.28816017093689 0.28816545338237

-0.10000000000000 0.28234366396114 0.28234937949911

0 0.27491051923462 0.27491630159737

?y'?y?2x/y计算实例二：对初值问题?取步长h=0.1;计算在[0，1.5]上的数值解。本

?y(0)?1

题的解析解为y??2x。

同样在计算机上，运用所编的程序进行了运算，结果如下，其中第一列为在区间上的等分点，第二列为运用R-K法的计算结果，第三列为Adams预测-校正法计算结果，第四列为精确解。

第二实例计算结果

0 1.00000000000000 1.00000000000000 1.00000000000000

0.10000000000000 1.09544553169309 1.09544553169309 1.09544511501033

0.20000000000000 1.18321674550599 1.18321674550599 1.18321595661992

0.30000000000000 1.26491222834039 1.26491222834039 1.26491106406735

0.40000000000000 1.34164235375037 1.34163505213867 1.34164078649987

0.50000000000000 1.41421557789009 1.41420723934048 1.41421356237310

0.60000000000000 1.48324222277199 1.48323305700166 1.48323969741913

0.70000000000000 1.54919645230214 1.54918577363467 1.54919333848297

0.80000000000000 1.61245534965899 1.61244282116642 1.61245154965971

.26.

0.90000000000000 1.67332465901626 1.67330987517170 1.67332005306815

1.00000000000000 1.73205636516557 1.73203885072786 1.73205080756888

1.10000000000000 1.78886106772579 1.78884027572849 1.78885438199983

1.20000000000000 1.84391691853791 1.84389219922183 1.84390889145858

1.30000000000000 1.89737622177080 1.89734679793772 1.89736659610103

1.40000000000000 1.94937040329812 1.94933534308208 1.94935886896179

1.50000000000000 2.00001381661027 1.99997200061724 2.00000000000000

根据计算结果，发现两种方法的结果与精确解很接近，精度均达到5位有效数字，但是R-K法运算是占用的内存要比Adams预测-校正法多，即其对计算机的要求要高一些，这与理论分析吻合。当然，四阶Adams预测-校正法的启动要由R-K法给出，即y0,y1,y2,y3的值需预先知道。

.27.