实验四  主成分分析与聚类分析

一、   实验目的

深入理解主成分分析的降维作用，熟练掌握用SPSS进行主成分分析的操作方法，对主成分的信息量、主成分载荷、主成分得分等概念有清晰的把握。

掌握地理对象聚类分析的基本原理，掌握不同聚类方法的操作方法和步骤，学会比较不同聚类方法的结果。

理解主成份分析在聚类分析中的应用。

二、   实验要求

1.          实验设备和仪器

a)         硬件：每人一台计算机，要求能够顺畅地运行SPPS软件

b)        软件：SPSS、EXCEL。

2.          实验数据

a)         21个农业区的经济生态数据；

上述该数据保存在“实验四数据.xls”文件中。

3.          实验报告

a)         完成实验内容及练习，按照规定的内容书写实验报告，要求阐明实验内容和结果，并对结果进行讨论。

三、   基本原理

1.        主成分分析的基本原理与计算步骤

（1）基本原理

主成分分析是一种通过线性变换构建综合性指标的方法，并对这些综合性指标依据信息量的大小进行排序，从而可以只选取信息量大的少数综合指标来反映地理系统，而抛弃信息量不多的其它指标，使得在信息量损失不多的情况下能够降低数据量，抓住系统主要特征。

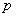假定有个地理样本，每个样本共有个变量，构成一个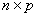阶的地理数据矩阵：

                                                                                        (4-1)

则我们希望通过线性变换的方法来构造一系列新的综合指标：

                                                                                   (4-2)

采用主成分分析方法，确定各个系数使得

①与相互无关（独立）；

②是的一切线性组合中方差最大者， 是与不相关的的所有线性组合中方差最大者；…；是与都不相关的的所有线性组合中方差最大者。

则新变量指标分别称为原变量指标的第1，第2，…，第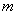主成分。

（2）主成份分析的计算步骤

主成分分析的计算步骤简列如下：

a)         计算相关系数矩阵；

b)        计算特征值与特征向量：

①       计算得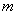个特征值；

②       对每个特征值，计算出相应的特征向量；

③       按特征值的大小排序，计算累计贡献率，当累计贡献率达85％y以上时，前几位的特征值所对应的第1、第2、第3、…主成份保留，其它可以忽略；

④       计算主成分载荷；

⑤       计算主成分得分。

2.        聚类分析

聚类分析是指根据地理事物各种要素取值的异同，采用某种数学方法定量地确定地理事物的距离，并按照这种距离对地理事物进行聚类。

（1）聚类分析之前的数据处理

在地理分类和分区研究中，被聚类的对象常常是多个要素构成的。不同要素的数据往往具有不同的单位和量纲，其数值的变异可能是很大的，这就会对分类结果产生影响。因此当分类要素的对象确定之后，在进行聚类分析之前，首先要对聚类要素进行数据处理。

①       总和标准化。

                                                               (4-3)

②       标准差标准化

                                                    (4-4)

③       极大值标准化

                                            (4-5)

④       极差的标准化

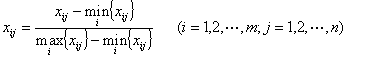                                       (4-6)

（2）距离的计算

经过标准化后，可以计算各个地理数据之间的距离，作为聚类的依据。通常用得比较多得距离有绝对距离和欧氏距离。

①       绝对值距离

                                                                     (4-7)

②       欧氏距离

                                                                           (4-8)

注意到，对于个地理对象，可以求得每一对对象之间的距离，从而构造出距离矩阵。

(3) 聚类方法

有了距离矩阵后，可以采用不同的方法进行聚类，一般有直接聚类法、最短距离聚类法、最远距离聚类法等等。可参见徐建华的《计量地理学》（徐建华，2006）。

四、   实验内容

1.        聚类分析

徐建华《计量地理学》附录光盘中“practice”文件夹中的“PDF”子文件夹中有一个“8.pdf”，是关于聚类分析的。打开该文件，按照其用SPSS进行聚类分析的步骤进行实验。注意：其中的数据采用农业区数据。关于在SPSS中如何进行聚类分析，以及相关参数设置的意义，见PPT《用SPSS进行聚类分析》。

2.        主成分分析

按9.pdf进行。数据同上。并参见《用SPSS进行因子分析》。

3.        主成分分析与聚类分析结合进行综合分析

既然主成分能够尽量地用较少的变量来反映大部分的信息，并且这些变量相互独立，分别描述地理事物的一个方面的内容，因此，我们在对地理事物进行聚类之前，可以先进行主成分分析，然后再根据前面几个主成分开展聚类分析。

先根据9.dbf进行主成分分析，再利用前3个主成分进行聚类分析。将结果与单独进行聚类分析的结果进行比较，回答以下问题：

（1）       最先三次的聚类是否不同？分别是由哪些区聚为一类的？

（2）       全部聚成一大类的聚类距离分别是多少？

（3）       你认为哪种聚类更合理？为什么？

参考文献：

1、  徐建华，计量地理学，高等教育出版社，2006，北京

第二篇：主成分分析与因子分析聚类分析

分类号 密 级 编 号1 0 4 8 6 U D C

武汉大学

硕士学位论文

主成分分析、因子分析和聚类

分析的比较与应用

研 究 生 姓 名：杨 武

学 号：200722010063

指导教师姓名、职称：冯 慧 教 授

学 科 、专 业 名称：计 算 数 学

研 究 方 向：数值分析及其应用

二零零九 年 五 月 日

The comparison and application of principal component analysis, factor

analysis and cluster analysis

Yang wu

郑 重 声 明

本人的学位论文是在导师指导下独立撰写并完成的，学位论文没有剽窃、抄袭、造假等违反学术道德、学术规范和侵权行为，否则,本人愿意承担由此而产生的法律责任和法律后果，特此郑重声明。

学位论文作者（签名）：

年 月 日

摘 要

主成分分析就是将多项指标转化为少数几项不相关的综合指标，在尽量保留原始信息的基础上用综合指标来解释多变量的方差-协方差结构；因子分析是研究如何以最少的信息丢失，将众多原始变量浓缩成少数几个因子变量，以及如何使因子变量具有较强的解释性的一种多元统计方法；聚类分析是依据数据本身所具有的定性或定量的特征来对数据分组归类以了解数据集的内在结构，并且对每个数据集进行描述的过程。它们在数据分析中有着广泛的应用。

本文主要作了如下的工作：

（1）介绍了主成分分析、因子分析和聚类分析的基本理论及应用过程、步骤；

（2）应用以上三种方法作一具体的实例分析，通过分析结果的对比，指出主成

分分析中的综合评价函数使用的局限性；

（3）在实例分析的过程当中及结束语中，对主成分分析、因子分析及聚类分析

的区别和联系给出了笔者的见解。

关键词：主成分分析 因子分析 聚类分析 综合评价函数 得分

I

ABSTRACT

Principal component analysis translated Multi-indicators into some un related composite indicators, and use these composite indicators to explain the multi-variable variance - covariance structure In the basis of retaining the original information as much as possible. Factor analysis is a multivariate statistical method which study on how to condense large number of original variables into a few enrichment factor variables at the least loss of information, and make the factor can be explained easily. Cluster analysis clustering the data based on the qualitative or quantitative characteristics of the data itself to describe and understand the internal structure of data sets. they are widely used in data analysis.

The main Content of this paper are as follows:

(1)Introduced the basic theory and application process of principal component analysis, factor analysis and cluster analysis;

(2) Analysis are made on a specific example with the three methods,

and pointed out the limitations of the comprehensive evaluation function in the principal component analysis By the contrast of the result produced above.

(3)In the process of analysis about the example and the last chapter, the difference and affiliation of principal component analysis, factor analysis and cluster analysis are given by the author.

Key words: principal component analysis, factor analysis, cluster analysis, comprehensive evaluation function, scores.

II

目 录

摘要 ……………………………………………………………………………………………Ⅰ ABSTRACT………………………………………………………………………………….Ⅱ 1 绪论……………………………………………………………………………………………1

1.1 研究背景及意义……………………………………………………………………………1

1.2 主成分分析、因子分析和聚类分析简介 ……………………………………………1

1.3 本文的主要工作……………………………………………………………………………4 2 主成分分析…………………………………………………………………………………5

2.1 主成分分析的数学模型及几何解释 ………………………………………………….5

2.2 总体主成分………………………………………………………………………………….6

2.3 样本主成分及其得分…………………………………………………………………….10 3 因子分析 ………………………………………………………………………………….12

3.1 因子分析的数学模型及其性质 ………………………………………………………12

3.2 因子载荷矩阵A=(aij)pm的统计意义.……………………………………………….13

3.3 因子载荷矩阵的求解 …………………………………………………………………14

3.4 因子旋转 ………………………………………………………………………………….18

3.5 因子得分 ………………………………………………………………………………….19 4 聚类分析 ………………………………………………………………………………….22

4.1 样品间相近性的度量…………………………………………………………………….22

4.2 类的几个定义和类的特征 …………………………………………………………….23

4.3 类间距离 ………………………………………………………………………………….24

4.4 类的各种统计量…………………………………………………………………………..27

4.5 谱系聚类法(系统聚类法)……………………………………………………………….29 5 实例分析 …………………………………………………………………………………30

5.1 指标及原始数据的初步处理 …………………………………………………………30

5.2 主成分分析 ………………………………………………………………………………35

5.3 因子分析 …………………………………………………………………………………39

5.4 聚类分 析…………………………………………………………………………………49 6 结束语 …………………………………………………………………………………….61

6.1 本文总结 ………………………………………………………………………………….61

6.2 建议与展望 ………………………………………………………………………………64 参考文献 …………………………………………………………………………………….65 致谢……………………………………………………………………………………………..67

第1章 绪论

1.1 研究背景及意义

主成分分析、因子分析和聚类分析是三种比较有价值的传统的多元统计方法，被广泛地应用于各行各业的数据分析当中。从政府管理决策、商业经营、科学研究到工业决策支持等各个领域都有它的用武之地。如基于客户数据库的市场营销，其中包括零售业的市场营销、信用卡业的市场营销、电信业的市场营销、保险业及其他企业的营销和客户关系管理等，通过应用这些方法将产品或顾客分类，从而以更好的服务留住客户、用更低的成本争取到新的客户并扩大市场份额，放弃信用差的客户，降低运营成本和风险；风险和欺诈检测，它可以协助进行风险评估、财务计划及资产评价、资源计划和竞争策略选择等；以及在体育、教育、军事、医药和生物、传媒、科学实验及在其它许多场合的应用等。正是因为应用范围之广，有关这三种方法的应用的论文也是非常之多，只是更换了一下数据即是。因此，正确使用主成分分析、因子分析和聚类分析就显得尤其重要。然而，目前的现状是，由于这些方法操作上的简单，以致不怎么了解该方法的理论与原理而仅仅依靠某些统计分析或数据挖掘软件就进行相关分析，这样的做法是不可取的。在某些文章当中，甚至将主成分分析和因子分析两者都用混了。还有，主成分分析中的一种流行的所谓的综合评价函数的方法，笔者认为此法缺乏足够的理论支持，至少笔者查阅了较多相关资料，没有找到理论上的证明，同时应用此法写作论文的作者们也没有给出相关分析。但是，这种综合评价函数却得到大量使用。有鉴于此，本文希望通过一个实例分析，对该方法的应用过程及其原理作一阐述，并在某些问题上提出自己的一些理解，笔者认为这项工作有一定的实际意义。

1.2 主成分分析、因子分析和聚类分析简介

这里先对这三种方法作一概括性的介绍，然后再在接下来的三章就基于统计方法的这三类分析法分别作较详细地介绍。

1.2.1主成分分析一瞥

主成分概念首先由Karl parson在19xx年引进，不过当时只对非随机变量来

1

讨论的。19xx年Hotelling将这个概念推广到随机向量。

在实际问题中，研究多指标(变量)问题是经常遇到的，且不同指标之间有一定相关性。由于指标较多再加上指标之间有一定的相关性，势必增加了分析问题的复杂性。主成分分析就是设法将原来指标重新组合成一组新的不相关的几个综合指标来代替原来指标，同时根据实际需要从中取几个较少的综合指标来尽可能多地反映原来指标的信息。这种将多个指标化为少数互不相关的综合指标的统计方法叫做主成分分析或称主分量分析。它也是数学上处理降维的一种方法。

主成分分析就是设法将原来众多具有一定相关性的指标(比如p个指标)，重新组合成一组新的相互无关的综合指标来代替原来指标，其最简单的形式就是取原来变量指标的线性组合。如果将选取的第一个线性组合即第一个综合指标记为F1，则希望F1尽可能多的反映原来指标的信息，这里的“信息”用方差来表达，即Var(F1)越大， 包含的信息越多。因此在所有的线性组合中所选取的F1应该是方差最大的，F1称为第一主成分。如果F1不足以代表原来p个指标的信息，再考虑选取F2即选第二个线性组合，为有效地反映原来信息， 已有的信息就不需要再出现在F2中，即（F1，F2）＝0，且F2的方差尽量大，称F2为第二主成分。依此类推可以构造第三，四，…，第p主成分。这些主成分之间不仅不相关，而且它们的方差依次递减。因此在实际应用中，就挑选前几个主成分，虽然这样做会损失一部分信息，但是由于它使我们抓住了主要矛盾，并从原始数据中进一步提取了某些新的信息。

1.2.2 因子分析一瞥

因子分析在其全部历史上时时机激起相当激烈的争论，它的现代起源在20世纪早期，K.皮尔逊（Pearson）,C.斯皮尔曼（Spearman）及其他一些学者，为定义和测定智力所作的努力。因为与智力这类概念早有联系，主要由对心理测量学有兴趣的科学家们，培育和发展了因子分析。对几个早期的心理学解释的争论以及缺乏强有力的计算工具，阻碍了它作为统计学方法的发展。伴随着计算机技术的高速发展，已经重新引发对因子分析的理论和计算方面的兴趣。原先的大部分技巧已经被抛弃，而紧随新近的发展，早期的争论也消退了。

因子分析（Factor Analysis）是主成分分析的推广，它也是从研究相关矩阵内部的依赖关系出发，把一些具有错综复杂关系的变量归结为少数几个综合因子

2

的一种多变量统计分析方法。具体地说，就是要找出某个问题中可直接测量的、具有一定相关性的诸指标，如何受少数几个在专业中有意义，又不可直接测量到，且相对独立的因子支配的规律，从而可用诸指标的测定来间接确定诸因子的状态。因子分析的目的是用有限个不可观察的潜在变量来解释原变量间的相关性或协方差关系。不可观察的潜在变量称为公共因子（common factor），它是所有变量共同具有的，除此每个变量还有不能用公共因子来表达的部分，称为特殊因子，它是每个原始变量独自具有的。因子分析是要利用少数几个公共因子去解释较多个观测变量中存在的复杂关系，它和主成分分析不同，不是对原始变量的重新组合，而是对原始变量进行分解，即分解为公共因子与特殊因子。由于因子分析是寻找潜在的起支配作用的因子即公共因子，而忽视了特殊因子，所以因子分析只能解释部分变异，而主成分分析可以解释所有变异。

1.2.3 聚类分析一瞥

聚类分析又称群分析，它是研究（样品或指标）分类问题的一种多元统计方法。所谓类，就是指相似元素的集合。聚类分析起源于分类学，在考古的分类学中，人们主要依靠经验和专业知识来实现分类。随着生产技术和科学的发展，人类的认识不断加深，分类越来越细，要求也越来越高，有时光凭经验和专业知识是不能进行确切分类的，往往需要定性和定量分析结合起来去分类，于是数学工具逐渐被引进分类学中，形成了数值分类学。19xx年，由Robert Sokal和Peter

of Numerical Taxonomy》一书对聚类的研究起了很大Sneath合著的《Principles

的推动和促进作用。后来随着多元分析的引进，聚类分析又逐渐从数值分类学中分离出来而形成一个相对独立的分支。

传统的聚类方法主要基于统计学和模式识别。聚类分析作为统计学得一个分支，主要研究方法是基于距离的聚类，以统计分析为基础的AutoClass就是这类方法的代表。在模式识别中，聚类分析常被称为非监督的学习或者概念聚类，它不仅考虑对象间的距离，还要求同类的对象具有某种共同的内涵。从这个意义上看，聚类分析就是将一组数据分组，使其具有最大的组内相似性和最小的组间相似性。

聚类分析是多元统计分析中研究“物以类聚”的一种方法，用于对事物的类别面貌尚不清楚，甚至在事前连总共有几类都不能确定的情况下进行分类的场合。聚类分析把分类对象按一定规则分成组或类，这些组或类不是事先给定的而是根据数据特征而定的。

聚类分析一般有两种类型，即按样品聚类和按变量聚类，其基本思想是通过定义样品或变量间“接近程度”的度量，以此为基础，将“相近”的样品或变量

3

归为一类。在一个给定的类里的这些对象在某种意义上倾向于彼此相似，而在不同类里的这些对象倾向于不相似。

迄今为止，人们已经提出了许多聚类的算法，如一些传统的聚类方法，空间数据的聚类方法和统计学中的聚类算法等，而且还不断地有新的算法被提出来，如神经网络、遗传算法、模糊聚类等等。近年来，聚类作为一种基本的数据分析、挖掘方法被广泛地应用于相似搜索、顾客划分、趋势分析、金融投资，地理信息系统、遥感图像和信息检索等领域中，对促进经济和科学研究事业的发展起着重要的作用。

1.3 本文的主要工作

正如1.1节所说，在目前还存在着主成分分析和因子分析法混淆的情况。某些统计分析件如SPSS，没有独立的主成分分析模块，而是将它放在因子分析模块中，调用两种分析都是使用FACTOR过程。在这个过程中，若全部采用默认状态或仅仅改变提取公因子个数一项，进行的将是主成分分析。而且，在根据具体数据求解因子模型的相关参数时，主成分法可以作为因子分析的一种方法出现，利用主成分法求得的因子载荷矩阵也就很容易认为是主成分分析模型的系数矩阵，事实上主成分分析的系数矩阵和因子分析的因子载荷矩阵的确很相似。两者还有许多步骤也是相同的，如指标的正向化、标准化，计算相关系数矩阵及其特征值、特征向量，用累计贡献率确定主成分个数及因子个数，单个主成分与综合主成分的分析评价、单因子与综合因子的分析评价步骤等。而聚类分析之所以在这里并提，是因为聚类分析是通过一个大的对称矩阵来探索相关关系，并据此分类，使类间的相关性尽量小，类内的相关性尽量大，对变量的聚类，和因子分

析有着较大的相似性。主成分得分和因子得分也可以作为聚类分析的数据来源。

为此，本文主要作了如下的工作：

（1）介绍了主成分分析、因子分析和聚类分析的基本理论及应用过程、步骤； （2）应用以上三种方法作一具体的实例分析，通过分析结果的对比，指出主成

分分析中的综合评价函数的使用局限性；

（3）在实例分析的过程当中及结束语中，对主成分分析、因子分析及聚类分析

的区别和联系给出了笔者的见解。

4

第2章 主成分分析

2.1主成分分析的数学模型及几何解释

设有n个样品，每个样品有p项指标(变量)，我们把这p个指标看作p个随机变量，记为X1，X2，…，XP,并记X=(X1,X2,L,,Xp)T,则X为随机向量。设第i个样品的第j个指标的观测值为xij，则原始数据资料阵为

?x11??x21 ?M??x?n1x12Kx1p??x22Lx2p? （2.1） MMM??xn2Lxnp??

每个观测到的样本可记为xi=(xi1,xi2,L,xip)T,i=1,2,Ln。

主成分分析就是要把这p个指标的问题，转变为讨论p个指标的线性组合的问题，而这些新的指标F1，F2，…，Fk (k≤p），按照保留主要信息量的原则充分反映原指标的信息，并且互不相关。即：

T?F1=a1X=a11X1+a12X2+L+a1pXp?T?F2=a2X=a21X1+a22X2+L+a2pXp?L??Fp=aT

pX=ap1X1+ap2X2+L+appXp? （2.2）

Cov(Fi,Fj)=0(i,j=1,2,Lp,i≠j),

Var(F1)≥Var(F2)≥L≥Var(Fp)

为了方便，讨论p=2时主成分的几何意义。 设有n个样品，每个样品有两个指标X1和X2，在由变量X1和X2所确定的二维平面中, n个样本点所散布的情况如椭圆状(若X~N(?,∑),即二元正态分布)。

5

（图2.1） 由图可知这n个样本点无论是沿着X1轴方向或X2轴方向都具有较大的离散性，其离散的程度可以分别用观测变量X1的方差和X2的方差定量地表示。如果只考虑X1或X2中的任何一个，那么包含在原始数据中的信息将会有较大的损失。由于在椭圆的长轴方向数据具有最大的分散性，即该方向上所反映的数据间的差异的信息最多，若取椭圆长轴方向为F1方向，椭圆短轴方向为F2方向，则这相当于在平面上作一个坐标变换，即按逆时针方向旋转某一角度，记为θ，根据旋轴变换公式新老坐标之间有关系，有

?F1??cosθ?F1=X1cosθ+X2sinθ?，即 ???F??=?FXsinθXcosθ=?+12?2???sinθ?2sinθ??X1????X??=PX （2.3） cosθ???2?

?cosθP=???sinθ?sinθ??为正交矩阵。 ?cosθ?

忽略如果上图的椭圆是相当扁平的，那么我们可以只考虑F1方向上的波动，

F2方向的波动。一般地，p个变量组成p维空间，n个样本就是p维空间的n个点，对p元正态分布变量，找主成分的问题就是找p维空间中椭球体的主轴问题。

2.2 总体主成分

2.2.1．总体主成分的定义

设X=(X1,X2,LXP)T为p维随机向量，其协方差矩阵为：

Cov(X)=∑=(σij)pp=E[(X?E(X))(X?E(X)T)] （2.4）

6

它是一个p阶非负定矩阵，按照主成分分析的思想，首先构造 X1,X2,L,Xp的线性组合

TX=a11X1+a12X2+L+a1pXP （2.5） F1=a1

TT确定a1=(a11,a12La1p)T，使得Var(F1)=Var(a1X)=a1Σa1达到最大。由于求主成

分实际上是对原坐标轴作正交旋转，可设a1为单位向量。由此a1确定的随机变量式2.5称为X的第一主成分。

如果第一主成分F1在a1上的分散性还不足以反映原变量的分散性（或称为信息），则再构造X1，X2，…，Xp的线性组合

T F2=a2X=a21X1+a22X2+L+a2pXP （2.6）

为使F1、F2反映的原变量的信息不重叠，要求F1、F2不相关，即

TTTCov(F2,F1)=Cov(a2X,a1X)=a2Σa1=0

由此单位向量a2确定的随机变量式2.6称为X的第二主成分。

一般地，若F1，F2…Fk?1还不足以反映原变量的信息，则继续构造X1，X2，…，Xp的线性组合

T Fk=akX=ak1X1+ak2X2+L+akpXP （2.7）

TTT在约束条件akak=1及akΣai=0（i=1,2,L,k?1）下，求ak使Var(Fk)=akΣak达

到最大。由此ak确定的随机变量式2.7称为X的第k主成分。 按上述方法，我们可以构造出p个方差大于零的主成分。

2.2.2 总体主成分的求法

关于总体主成分有如下结论：设X=(X1,X2,LXP)T的协方差矩阵∑的特征

相应的正交单位化特征向量为e1,e2,Lep，则X的第k值为λ1≥λ2≥L≥λp≥0，

个主成分可表示为

7

T Fk=ekX=ek1X1+ek2X2+L+ekpXP（k=1,2,Lp） （2.8）

其中ek=(ek1,ek2,Lekp)T ，且有

TT??Var(Fk)=ek∑ek=λkekek=λk,k=1,2,Lp?TTCovFF=e∑e=e(,)λ?jkjkkjek=0,j≠k （2.9） ?

证明：令P=(e1,e2,Lep)，则P为正交矩阵，且PT∑P=Λ=Diang(λ1,λ2,Lλp)

TT若F1=a1X=a11X1+a12X2+L+a1pXP为X的第一主成分，其中a1a1=1，令

TTTz1=PTa1=(z11,z12,L,z1p)T，则z1z1=a1PPTa1=a1a1=1，且

TTTTVar(F1)=Var(a1X)=a1Σa1=z1P∑Pz1

T22=λ1z11+λ2z12+Lλpz12p≤λ1z1z1=λ1

T且当z1=(1,0L,0)T时，等号成立，这时a1=Pz1=e1。所以在约束条件a1a1=1之

下，当a1=e1时Var(F1)达到最大，且

TTmax{var()}F=Var(eX)=eΣe1=λ1 111Ta1a1=1

T设F2=a2X为X的第二主成分，则应有

TTTTTa2a2=1且Cov(F2,F1)=Cov(a2X,e1X)=a2Σe1=λ1a2e1=0

T首先选择a2与e1正交，即a2e1=0，令z2=PTa2=(z21,z22,L,z2p)T，则

TTTTz2z2=a2PPTa2=a2a2=1，而由a2e1=0即有

TTTTTa2e1=z2Pe1=z21e1e1+z22e2e2+…+z2peT

pep=z21=0

所以

TTTTVar(F2)=Var(a2X)=a2Σa2=z2P∑Pz2

T222Λz2=λ1z21+λ2z22+Lλpz2=z2p

T22=λ2z22+Lλpz2p≤λ2z2z2=λ2

T当z2=(0,1,0,L,0)T时，即a2=Pz2=e2时，满足a2a2=1，且

TTTTCov(F2,F1)=Cov(a2X,e1X)=a2Σe1=λ1a2e1=0，并且使Var(F2)达到最大。同理，

8

X的各主成分都可按上述过程求得。

即求X的主成分等价于求它的协方差矩阵∑的所有特征值和相应的单位正交化特征向量。按特征值由大到小所对应的单位正交化特征向量为组合系数的X1,X2,L,Xp的线性组合分别为X的第一、第二、直至第p个主成分，而各主成分的方差等于相应的特征值。

2.2.3 总体主成分的性质

1.5.3.1主成分的协方差矩阵及总方差

记F=(F1,F2,L,Fp)T为p个主成分构成的随机向量, P=(e1,e2,L,ep)为∑的p个单位正交化特征向量构成的正交矩阵，则

F=PTX，Cov(F)=Cov(PTX)=PT∑P=Diang(λ1,λ2,L,λp)

∑Var(F)=∑λk

k=1ppkk=1=Tr(∑)=∑Var(Xk) （2.10） k=1

pp

主成分分析把p个原始变量X1,X2,L,Xp的总方差∑Var(Xk)分解成p个不相

k=1

关变量F1,F2,L,Fp的方差和，且使得Var(Fk)=λk，k=1,2,Lp

1.5.3.2主成分的贡献率与累计贡献率

λi/∑λi=Var(Fk)/∑Var(Xi) （2.11）

i=1i=1pp

称为Fk的贡献率，它描述了Fk提取的X1,X2,L,Xp的总（分散性）信息的份额。由λ1≥λ2≥L≥λp≥0知，F1,F2,L,Fp综合原始变量的能力依次递减。 ∑λ/∑λ=∑Var(F)/∑Var(Xiii

i=1i=1i=1k=1mpmpp) （2.12）

称为F1,F2,L,Fm的累计贡献率，它描述了F1,F2,L,Fp综合X1,X2,L,Xp的总（分散性）信息的能力。在应用中常取m≤p，使F1,F2,L,Fm的累计贡献率达

，则用F1,F2,L,Fp代替X1,X2,L,Xp不但可以使到一定的比例（如80%—90%）

原变量的维数降低，而且也不至于损失原始变量中太多的信息。

9

2.2.4 标准化变量的主成分

不同的变量往往有不同的量纲，从而引起各变量取值的分散程度差异较大，这时变量的总方差主要受方差较大的变量控制。为了消除原始变量彼此方差差异过大的影响，通常将原始变量进行标准化再做主成分分析。

对于X=(X1,X2,L,Xp)T，设?k=E(Xk)，σkk=Var(Xk)，k=1,2,Lp，则其标准化变量为

?= XkXk??kkk，k=1,2,Lp （2.13）

????T则E(Xk)=0，Var(Xk) =1，k=1,2,Lp。令X?=(X1?,Xk,L,Xk)，ρ为其协方差矩阵，则

ρ=(ρij)pp=Cov(X?)，ρij =E(Xi?X?

j)=Cov(Xi,Xj)

iijj （2.14）

即ρ为X的相关系数矩阵。对标准化向量X?作主成分分析即求X的相关系数矩阵ρ的特征值及相应的单位正交化特征向量。

2.3 样本主成分及其得分

在实际问题中，总体X=(X1,X2,L,Xp)T的协方差矩阵∑（或相关系数矩阵R）一般是未知的，具有的资料只是来自于X的一个容量为n的样本观测数据 xi=(xi1,xi2,L,xip)T,i=1,2,Ln。这时我们用其样本协方差矩阵S或其样本相关系数矩阵R分别作为∑或ρ的估计进行主成分分析,而由S或R求得的主成分称为样本主成分。其中

sjk1nTS=(sjk)pp=∑(xi?x)(xi?x),R=(rij)pp=(sspp n?1i=1jjkk

1n

x=(x1,x2,L,xp)，xj=∑xij，j=1,2,Lp （2.15） ni=1T

1n

sjk=(xij?xj)(xik?xk)T，j,k=1,2,Lp ∑n?1i=1

10