专业实习报告
题 目: 基于马氏距离的K-均值聚类法
院 系: 数学与计算机科学学院
专 业: 数学与应用数学 ____ _
年 级: 2009级 ______
学 号: 030901439
姓 名: 曾丹萍
指导教师: 吕书龙 _
实习地点: 福州大学 __
20##年01月12日
基于马氏距离的K-均值聚类方法
摘要:K-均值聚类算法为大样本聚类问题提供了较优的解决方案,但是它将样本矢量对聚类结果的贡献看做是一样的,这在处理属性高相关的数据集时,出错的概率自然就增大了。针对这个问题,本文简单设计了一种基于马氏距离的K-均值聚类方法,利用马氏距离的优点对属性高相关的数据集进行更有效的分类。再有K-均值聚类对初始凝聚点比较敏感,本文提出用样本间距离散点图的方法选取初始凝聚点,并同时确定类间最小距离C和类内最大距离R。实验证明想法是对,但基于马氏距离里的协方差阵并不是都可逆,替代后效果并不是太理想,且计算时间偏慢,这只能待以后再研究。
关键词:K-均值聚类,马氏距离,初始凝聚点
一、引言
聚类分析是一种重要的数据分析技术,它是将物理或抽象对象的集合分组成为由类似的对象组成的多个类的过程。目前常用的聚类算法可分为以下几种:分裂法,如K-means、K-medoid算法等;层次法,代表性算法如CURE算法等;基于密度的方法,典型算法有DBSCAN算法、OPTICS算法等;基于网格的方法,如STING算法、CLIQUE算法等;于模型的方法,如SOM算法等。其中,K-means算法由于其方法简单,已成为当前最流行的聚类算法之一。K-means是一种基于划分的聚类算法,目的是通过在完备数据空间的不完全搜索,使得目标函数取得最大值。
K-均值聚类算法对初始凝聚点敏感,从不同的初始凝聚点出发,得到的聚类结果也不一样。如何选取较好的初始凝聚点,从而获得更好聚类效果,是本文的一个出发点。
K-均值聚类使用的是欧氏距离,即假定待分析样本矢量的各维特征对分类贡献均匀,不考虑各个特征重要度对分类的影响。然而实际应用中,类属性数据和混合型数据的样本分布是非均匀或非对称的,属性对分类的贡献是不均匀的,甚至有些属性起到冗余作用。本文采用马氏距离作为计算样本到凝聚点的距离
二、K-均值聚类法
2.1 K-均值聚类的思想
K-均值聚类法是J.B.MacQueen 在 1967 年提出,是动态聚类的一种,又可称逐个修改法。其基本思想是,开始先粗略地的分一下类,然后按照某种最有的原则修改不合理的凝聚点,然后对每一个样品进行分类后,立即改变凝聚点,再考虑下个样品,直至类分得比较合理为止,这样就形成了一个最终的分类结果。
用数学语言表达可以说,K-均值聚类算法是基于划分的聚类方法,采用聚类误差平方和函数E作为聚类准则函数,其中,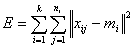 ,
,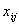 是第
是第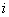 类第
类第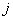 个样本,
个样本,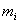 是第
是第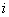 类的聚类中心或称质心,
类的聚类中心或称质心,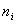 是第
是第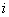 类样本个数。K-均值聚类算法实质就是通过反复迭代寻找
类样本个数。K-均值聚类算法实质就是通过反复迭代寻找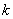 个最佳的聚类中心,将全体
个最佳的聚类中心,将全体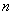 个样本点分配到离它最近的聚类中心,使聚类误差平方和
个样本点分配到离它最近的聚类中心,使聚类误差平方和 最小。
最小。
2.2 K-均值聚类的步骤
步骤1:规定样品间的距离,人为地定出三个数:K(分类数),C(类间距离的最小值)和R(类内距离的最大值);取前K个样品点作为凝聚点。
步骤2:计算着K个凝聚点两两之间的距离,如最小的距离<C,则将相应的两个凝聚点合并,用这两个点的重心作为新的凝聚点,再重复步骤2,直至所有凝聚点之间的距离均≥C为止。
步骤3:将剩下的n-K个样品逐个归类,对每一个样品,计算该样品与所用凝聚点的距离,如最小距离>R,则该样品作为新的凝聚点;如最小距离≤R,则将该样品归入与它距离最近的凝聚点所在的类,随即重新计算这一类的重心,以重心作为新的凝聚点。如凝聚点之间的距离都≥C,则考虑下一个样品,否则用步骤2进行合并后再考虑下一个样品,直至所有样品都归了类。
步骤4:将样品从头至尾再逐个按步骤3进行归类,不同之处是:某个样品归类后,如分类和原来的一致,则重心不必计算;如分类与原来不同,则涉及到的两类重心重新计算。如果新的分类与上一次相同,则聚类过程结束,否则重复步骤4。
2.3 K-均值聚类的优缺点
当数据样本集较大时,系统聚类过程往往会占据大量的计算机内存,并且所需的计算时间也很多,这就为应用带来一定的不变。因而K-均值聚类法以其方法思想的简单、计算量较少、占用计算机内存较少的优点应运而生,并已成为一种最常用的聚类算法之一。
但它的缺点也是很明显的。K-均值聚类算法对初始凝聚点敏感,从不同的初始凝聚点出发,得到的聚类结果也不一样,而往往它又是简单的样本前K个为初始凝聚点,这使得最终分类的不确定性更明显了。
2.4 样本距离散点图
由前面的分析可以知道样本的初始凝聚点对其最终的分类是有较大的影响,简单的选取前K个样品为初始凝聚点是蛮不合理的,最好选择些有代表的点,因此较准确地选择初始凝聚点是非常有用的。
通常选择初始凝聚点的方法有:①人为选择,即根据经验选择。显然这对大多数新学聚类的人来说是不适用的。②将样品分为K类,计算每类重心,以重心为初始凝聚点。③随机选择。这种不确定性也比较大。④用密度法选凝聚点等。
因为对图形直观表现力的偏爱,我想或许也可以用图来直观的选取初始凝聚点。于是,本文的初是凝聚点的选取将借助样本点间的距离散点图。具体步骤如下:①随意选取一个样本点(为方便,就选第一个样本点),计算该点到其他n-1个样品的距离。②画出距离散点图。③根据情况,适当调整图形,选择初始凝聚点,并确定分类数K、类间距离的最小值C和类内距离的最大值R。实验证明该方法可以较快较好的选择初始凝聚点。
三、马氏距离
3.1马氏距离
我们熟悉的欧氏距离虽然很有用,但也有明显的缺点。它将样品的不同属性(即各指标或各变量)之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中,经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。因此,有时需要采用不同的距离函数。
于是,印度统计学家马哈拉诺比斯(P.C.Mahalanobis)提出了马氏距离,它表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法,并且是尺度无关的(scale-invariant),即独立于测量尺度。
设总体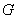 为
为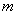 元总体,则样品
元总体,则样品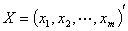 到总体
到总体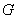 的马氏距离定义为:
的马氏距离定义为:
 ,
,
其中 是总体
是总体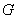 的均值向量,
的均值向量,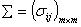 是总体
是总体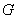 的协方差阵。
的协方差阵。
当 时,
时,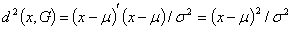 ,即标准化的欧氏距离。
,即标准化的欧氏距离。
3.2改进的马氏距离
有时,特别是样本数不够多的时候,这里的协方差矩阵 可能是奇异的,这将导致无法直接求马氏距离。有人提出此时,用欧氏距离代替,可这好像是回到的原点,不符合本文的立意。只好另找出路了。
可能是奇异的,这将导致无法直接求马氏距离。有人提出此时,用欧氏距离代替,可这好像是回到的原点,不符合本文的立意。只好另找出路了。
根据矩阵理论,任一秩为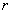 的实对称半正定矩阵都可以按下述方式分解:
的实对称半正定矩阵都可以按下述方式分解:
 为实对称半正定矩阵,设
为实对称半正定矩阵,设 的秩为
的秩为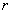 ,则可
,则可 以分解为
以分解为 ,
,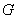 为
为 的对角阵,它由
的对角阵,它由 的非0特征值构成,
的非0特征值构成,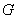 是非奇异的。
是非奇异的。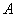 为
为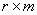 矩阵,由
矩阵,由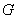 中特征值所对应的特征向量构成,它张成了
中特征值所对应的特征向量构成,它张成了 的非退化子空间,且
的非退化子空间,且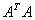 为
为 的单位阵。有了这一分解,便可根据
的单位阵。有了这一分解,便可根据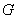 的逆来求
的逆来求 的伪逆:
的伪逆: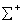 =
=
这样马氏距离就转化为: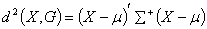 。
。
当然,还可以有其他的处理办法,就不再介绍了。
四、实例实验结果及方法比较
实验1:iris数据的聚类
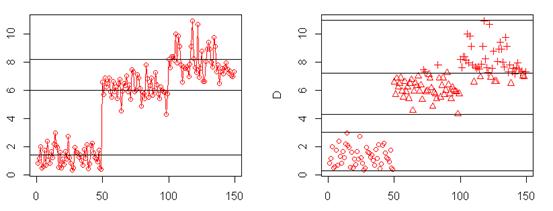 1.画样本距离散点图,确定分类数K、类间距离的最小值C、类内距离的最大值R及初始凝聚点。
1.画样本距离散点图,确定分类数K、类间距离的最小值C、类内距离的最大值R及初始凝聚点。
从图可以非常直观的看出,样本集可以分为3类,即初步确定K=3。再进步细分就可以估算出类间的最小距离和类内的最大距离,即确定C=2.2,R=3.8。并粗略选择初始凝聚点X[34,],X[76,],X[101,]
2.进行K-均值聚类
将选定的初始凝聚点排列到样本的最前面,再调用自编写的函数K_means(X,K,C,R),得到结果:
> km = K_means(X,K,C,R)#system.time(K_means(X,K,C,R))
>kk = kmeans(X,3);
> sum(kk$cl == rep(c(2,1,3),each = 100))/150*100
[1] 67.33333
>sum(km$G == rep(c(3,5,1),each = 50))/150*100
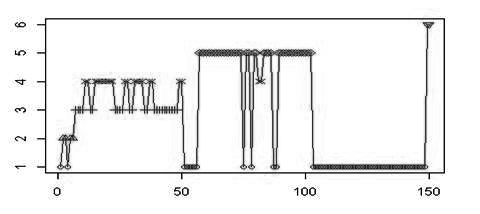
[1] 72
由结果的图和数据可以看出,最终的聚类效果还是比较接近原数据的分类情况的。且与常规的K-均值聚类比起准确率还提高了4.7%。这说明,基于马氏距离的K-均值聚类方法还是比较适合这组属性相关的iris样本集的。
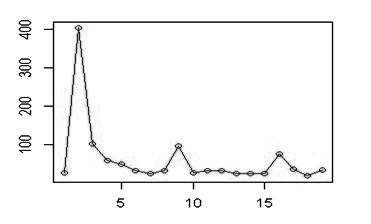
实验2:成绩数据的聚类
步骤基本与实验1一致,就不重复了。
由图看出第二个点特别突出,影响了其他点的观察,现将其暂时剔除,得到修正图:
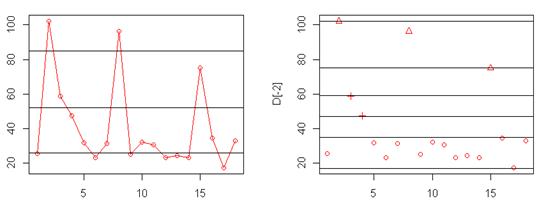
通过对这些图的分析得到,K = 4;,C = 27, R = 27,初始凝聚点定为X[2,],X[3,],X[5,], X[9,]。
> km = K_means(X,K,C,R)#system.time(K_means(X,K,C,R))
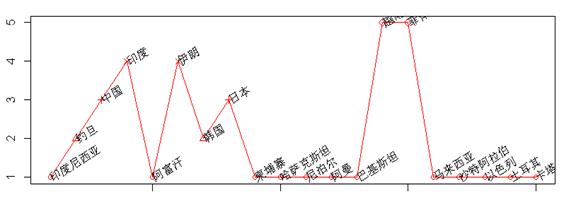
进行聚类后得到:
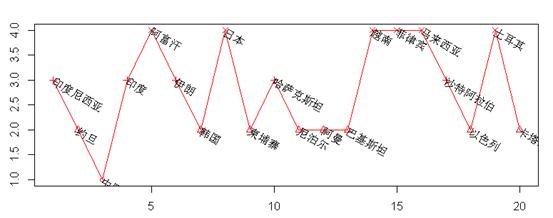
而常规的K-均值聚类结果为:
对比可以发现,两者间的聚类结果还是有许多交叉处的。但是自编的K_means()聚类函数,在聚类过程会根据规定的C、R进行调整分类个数,而常规的则没有。所以两者结果不尽相同,不同的人有不同的看法。而该数据本身也不具有非常明显的分类,所以对于这组数据谁好谁坏不好确定,也就不再深入研究了。
六、结论
本文针对K-均值聚类对初始凝聚点的敏感性,提出来距离散点图粗选初始凝聚点,通过实验证明,这还是种不错的尝试,且效果还不错。
基于欧式距离对属性相关数据部敏感的缺点,本文提出的用马氏距离代替计算距离,效果不是特别明显,对iris数据集也只多出了4.7%的正确率。对这个,与因马氏距离计算中的协方差阵 并不是均可逆,而采取了特征矩阵、特征值来代替有一定的关系。
并不是均可逆,而采取了特征矩阵、特征值来代替有一定的关系。
总之,虽然本文提出的方法并不是对大类数据样本集都有很好的效果,但却也是自己思考的结果,还是有一定的意义的,且对某些样本集效果还是可观的。
参考文献:
[1] 王慧,申石磊.一种改进的特征加权K-means聚类算法.微电子学与计算机.20##-07
[2] 谢娟英,蒋帅等.一种改进的全局K-均值聚类算法.陕西师范大学学报(自然科学版).20##-03
[3] 蔡静颖,谢福鼎等.基于马氏距离特征加权的模糊聚类新算法.计算机工程与应用.2012,48(5)
[4] 张翔,王士同.一种基于马氏距离的可能性聚类方法.数据采集与处理.20##-01
[5] 高惠璇.应用多元统计分析.北京大学出版社.2005
[6] 李庆扬,王能超,易大义.数值分析(第5版).清华大学出版社.2008
附录:
1.数据:
平均寿命 识字率 综合入学率 人均GDP 面积 人口
阿富汗 44.637 32.69196 54.07206 1419.003 652300 22000
柬埔寨 62.168 78.2879 58.07544 1952.26 181035 11430
中国 73.474 94.2301 68.005 7206.118 9600000 1295330
印度 64.352 68.2926 62.60772 3354.394 2974700 1020000
印度尼西亚 71.493 93.78223 74.51548 4394.326 1904443 210000
伊朗 71.91 85.23285 74.03589 11891.32 1645000 63900
韩国 79.8 99 99.84531 29325.77 99600 48022
日本 83.166 99 87.29832 33648.66 377800 127310
约旦 73.107 93.10328 78.26715 5700.399 89340 5040
哈萨克斯坦 65.364 99 90.93078 11927.25 2717300 14821
尼泊尔 67.459 60.3039 57.47862 1189.24 147181 23000
阿曼 76.142 86.2734 66.16027 26258.11 30950 2325
巴基斯坦 67.164 57.83466 41.53325 2624.715 11500 8797
越南 74.908 92.13669 63.71198 3096.957 329556 77680
菲律宾 72.339 93.6732 78.02884 3600.9 300000 80080
马来西亚 74.732 92.898 69.76717 14410.43 329735 23275
沙特阿拉伯 73.305 86.746 80.16356 24208.17 2250000 22760
以色列 81.153 98.42512 90.86705 28291.88 14900 6458
土耳其 72.23 90.03958 74.26163 13359.24 779450 66500
卡塔尔 75.966 94.34211 60.97165 77177.68 11437 580
2.程序代码:
##1
X = iris[,-5]
##2
#X = read.table("clipboard", header = TRUE)
X = as.matrix(X)
#############################################0
Mahalanobis = function(X,Y,Cov)
{
ok = complete.cases(Cov);
n1 = length(Cov); n0 = length(Cov[ok]);
if(n0 == n1)
{
t = eigen(Cov)
ve = t$vectors; va = t$values
m = length(va[va != 0])
G = matrix(0,nrow = m, ncol = m)
for(i in 1:m){ G[i,i] = 1/va[va != 0][i]; }
A = ve[va != 0,]
if(length(G) == 1){ S = t(A)%*%A*G; }
if(length(G) > 1) { S = t(A)%*%G%*%A; }
if(length(S) == 1){ D = t(X-Y)%*%(X-Y)*S; }
if(length(S) > 1){ D = t(X-Y)%*%S%*%(X-Y); }
}#if
else{ D = t(X-Y)%*%(X-Y);}
sqrt(abs(D));
}
##############################2
fun_Xt = function(i,j)
{
t = NA
t = X[i,]; X[i,] = X[j,]; X[j,] = t
t = NA
t = rownames(X)[i]; rownames(X)[i] = rownames(X)[j]; rownames(X)[j] = t
X
}
##############################################1
n = length(X[,1]); m = length(X[1,])
D = NA
for( i in 2:n){ D[i] = Mahalanobis(X[1,],X[i,],cov(X)); }
D = D[-1]
#par(mfrow = c(1,2))
plot(D, type = "o", col = "red");
##1
#plot(D[1:49), type = "o", col = "red");
#plot(D[50:99], type = "o", col = "red");
#plot(D[100:149], type = "o", col = "red");
#abline(h = c(1.4,6,8.2))
#plot(D, pch = c(rep(1,49),rep(2,22),3,3,rep(2,9),3,rep(2,16),rep(3,10),2,rep(3,4),2,rep(3,7),2,3,3,2,2,rep(3,10),2,rep(3,8),2,2,3), col = "red")
#abline(h = c(0.3,3,4.3,7.2,11))
#K = 3; C = 2.2; R = 3.8;
#X[34,],X[76,],X[101,]
#X = fun_Xt(1,34); X = fun_Xt(2,76); X = fun_Xt(3,101);
##2
#plot(D[-2], type = "o", col = "red");
#abline(h= c(85,52,26))
#plot(D[-c(2,3,9,16)], type = "o", col = "red");
#plot(D[-2], pch = c(1,2,3,3,1,1,1,2,1,1,1,1,1,1,2,1,1,1), col = "red")
#abline(h= c(102,75,59,47,35,17))
#K = 4; C = 27; R = 27;
#X[2,],X[3,],X[5,], X[9,]
#X = fun_Xt(1,5); X = fun_Xt(2,9)
##############################################3
fun_G = function(GX,GN,G,C)
{
ok = complete.cases(G);
k = length(GN); m = length(GX[1,]); n = length(G[ok]);
if( k == 1){return(list(GX = GX, GN = GN, G = G));}
D = matrix(NA, nrow = k-1, ncol = k);
for(i in 1:(k-1))
{
for(j in (i+1):k){ D[i,j] = Mahalanobis(GX[i,],GX[j,],cov(GX)); }
}#for i
min_d = min(D[!is.na(D)]);
#s = 0
while(k>1 && min_d < C)
{
for(i in 1:(k-1))
{
find = 0;
for(j in (i+1):k)
{
if(D[i,j] == min_d)
{
GX[i,] = (GX[i,]*GN[i] + GX[j,]*GN[j])/(GN[i] + GN[j])
GN[i] = GN[i] + GN[j]
if(j < k){ for(r in j:(k-1)){ GX[r,] = GX[r+1,]; GN[r] = GN[r+1]; }}
GX = GX[-k,]; GN = GN[-k];
for(r in 1:n)
{
if(G[r] == j){ G[r] = i; }
if(G[r] > j){ G[r] = G[r]-1; }
}
GX = matrix(GX, ncol = m)
k = k-1;
find = 1; break;
}#if
}#for j
if(find == 1){ break; }
}#for i
if(k == 1){ break; }
D = matrix(NA, nrow = k-1, ncol = k);
for(i in 1:(k-1))
{
for(j in (i+1):k)
{
D[i,j] = Mahalanobis(GX[i,],GX[j,],cov(GX))
}#for j
}#for i
min_d = min(D[!is.na(D)])
#s = s+1
#if(s>100){break;}
}#while
list(GX = GX, GN = GN, G = G)
}#fun_G
##########################################4
fun_X = function(X,K,C,R)
{
m = length(X[1,]); n = length(X[,1]);
GX = matrix(NA, nrow = K, ncol = m); GN = rep(1, K); G = rep(NA, n)
for(i in 1:K){ GX[i,] = X[i,] }
G[1:K] = 1:K;
fun_G0 = fun_G(GX,GN,G,C)
GX = fun_G0$GX; GN = fun_G0$GN; G = fun_G0$G;
for(i in (K+1):n)
{
k = length(GN);
D = rep(NA, k);
for(j in 1:k)
{
D[j] = Mahalanobis(X[i,],GX[j,],cov(as.matrix(X[!is.na(G == j) & G == j,])));
}#for j
min_d = min(D);
if(min_d > R)
{
GX = rbind(GX,X[i]); GN = c(GN,1); G[i] = k+1; k = k+1;
}#if
else
{
for(j in 1:k)
{
if(D[j] == min_d)
{
GX[j,] = ( GX[j,]*GN[j] + X[i,])/(1 + GN[j]);
GN[j] = 1 + GN[j];
G[i] = j;
}#if
}#for j
}#else GX;GN;G
G1 = fun_G(GX,GN,G,C);
GX = G1$GX; GN = G1$GN; G = G1$G;
}#for
list(GX = GX, GN = GN, G = G)
}#fun_X
###########################################5
fun_all_X = function(X,GX,GN,G)
{
n = length(X[,1]);k = length(GN);
if( k == 1){return(list(GX = GX, GN = GN, G = G));}
for(i in 1:n)
{
find = 0
D = rep(NA,k)
for(j in 1:k)
{
D[j] = Mahalanobis(X[i,],GX[j,],cov(as.matrix(X[!is.na(G == j) & G == j,])));
}#for j
min_d = min(D); r = G[i];
if(D[r] != min_d)
{
for(j in 1:k)
{
if(D[j] == min_d)
{
t = min(r,j); s = abs(r-j)
GX[t,] = ( GX[t,]*GN[t] + GX[t+s,]*GN[t+s])/(GN[t] + GN[t+s]);
GN[t] = GN[t] + GN[t+s];
if((t+s) < k){ for(p in (t+s):(k-1)){ GX[p,] = GX[p+1,]; GN[p] = GN[p+1];}}
GX = as.matrix(GX[-k,]); GN = GN[-k];
k = k-1; find = 1;
for(p in 1:n)
{
if(G[p] == r || G[p] == j){ G[p] = t; }
if(G[p] > (t+s)){ G[p] = G[p]-1; }
}#for p
}#if
}#for j
}#if
if(find == 1){ break; }
k = length(GN);
}#for
list(GX = GX, GN = GN, G = G);
}#fun_all_X
#############################################6
K_means = function(X,K,C,R)
{
G1 = fun_X(X,K,C,R)
GX = G1$GX; GN = G1$GN; G = G1$G;
G2 = fun_all_X(X,GX,GN,G)
#t = 0
while(length(G == G2$G) != length(X[,1]) )
{
GX = G2$GX; GN = G2$GN; G = G2$G;
G2 = fun_all_X(X,GX,GN,G)
#t = t+1;
#if(t > 100){ break; }
}#while
GX = G2$GX; GN = G2$GN; G = G2$G;
D = rep(0,length(GX[,1]))
for(i in 1:length(GX[,1]))
{
Y = as.matrix(X[!is.na(G == i) & G == i,]);
for(j in 1:length(X[G == i,1])){D[i] = D[i] + Mahalanobis(Y[j,],GX[i,],cov(Y)); }
}
colnames(GX) = colnames(X)
rownames(GX) = paste("G",1:length(G2$GX[,1]))
names(G) = rownames(X)
list(GX = GX, GN = GN, G = G,D = D);
}#K_means
#########################
km = K_means(X,K,C,R) #system.time(K_means(X,K,C,R))
km
##1
#K_means(X,K,3.4,3.1)
#plot(km$G, col = "red", type = 'o', pch = km$G)
#sum(km$G == rep(c(3,5,1),each = 50))/150*100
#kk = kmeans(X,3); sum(kk$cl == rep(c(3,2,1),each = 100))/300*100
#sum(cc$G == rep(c(1,2,3),each = 50))/150*100
##2
#K_means(X,K,30,17)
#plot(km$G, col = "red", type = 'o', pch = km$G)
#par(srt = 30)
#text(1:length(km$G),km$G, names(km$G),0)
# kk = kmeans(X,4);plot(kk$cl, col = "red", type = 'o', pch = kk$cl)
#par(srt = -30)
#text(1:length(kk$cl),kk$cl, names(kk$cl),0)
