椭圆与双曲线的对偶性质总结
椭 圆
1. 点P处的切线PT平分△PF1F2在点P处的外角.
2. PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相离.
4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.
5. 若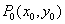 在椭圆
在椭圆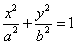 上,则过
上,则过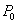 的椭圆的切线方程是
的椭圆的切线方程是 .
.
6. 若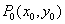 在椭圆
在椭圆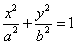 外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是 .
.
7. 椭圆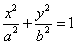 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点
(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点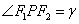 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为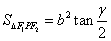 .
.
8. 椭圆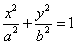 (a>b>0)的焦半径公式:
(a>b>0)的焦半径公式:
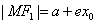 ,
,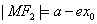 (
(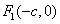 ,
, 
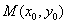 ).
).
9. 设过椭圆焦点F作直线与椭圆相交 P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.
10. 过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是椭圆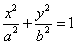 的不平行于对称轴的弦,M
的不平行于对称轴的弦,M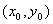 为AB的中点,则
为AB的中点,则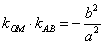 , 即
, 即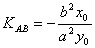 。
。
12. 若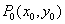 在椭圆
在椭圆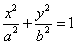 内,则被Po所平分的中点弦的方程是
内,则被Po所平分的中点弦的方程是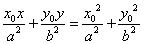 .
.
13. 若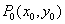 在椭圆
在椭圆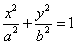 内,则过Po的弦中点的轨迹方程是
内,则过Po的弦中点的轨迹方程是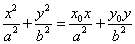 .
.
双曲线
1. 点P处的切线PT平分△PF1F2在点P处的内角.
2. PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相交.
4. 以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)
5. 若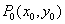 在双曲线
在双曲线 (a>0,b>0)上,则过
(a>0,b>0)上,则过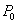 的双曲线的切线方程是
的双曲线的切线方程是 .
.
6. 若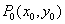 在双曲线
在双曲线 (a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
(a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是 .
.
7. 双曲线 (a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点
(a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点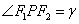 ,则双曲线的焦点角形的面积为
,则双曲线的焦点角形的面积为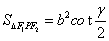 .
.
8. 双曲线 (a>0,b>o)的焦半径公式:(
(a>0,b>o)的焦半径公式:(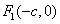 ,
, 
当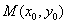 在右支上时,
在右支上时,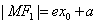 ,
,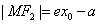 .
.
当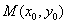 在左支上时,
在左支上时,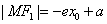 ,
,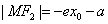
9. 设过双曲线焦点F作直线与双曲线相交 P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.
10. 过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是双曲线 (a>0,b>0)的不平行于对称轴的弦,M
(a>0,b>0)的不平行于对称轴的弦,M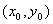 为AB的中点,则
为AB的中点,则 ,即
,即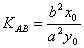 。
。
12. 若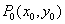 在双曲线
在双曲线 (a>0,b>0)内,则被Po所平分的中点弦的方程是
(a>0,b>0)内,则被Po所平分的中点弦的方程是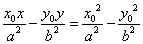 .
.
13. 若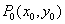 在双曲线
在双曲线 (a>0,b>0)内,则过Po的弦中点的轨迹方程是
(a>0,b>0)内,则过Po的弦中点的轨迹方程是 .
.
椭圆与双曲线的经典结论
椭 圆
1. 椭圆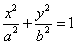 (a>b>o)的两个顶点为
(a>b>o)的两个顶点为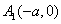 ,
,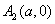 ,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是 .
.
2. 过椭圆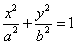 (a>0, b>0)上任一点
(a>0, b>0)上任一点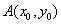 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且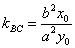 (常数).
(常数).
3. 若P为椭圆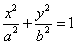 (a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,
(a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,  ,
, 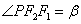 ,则
,则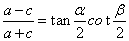 .
.
4. 设椭圆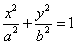 (a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记
(a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记 ,
, 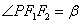 ,
, ,则有
,则有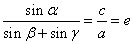 .
.
5. 若椭圆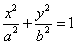 (a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤
(a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤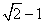 时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为椭圆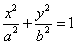 (a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则
(a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则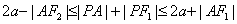 ,当且仅当
,当且仅当 三点共线时,等号成立.
三点共线时,等号成立.
7. 椭圆 与直线
与直线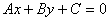 有公共点的充要条件是
有公共点的充要条件是 .
.
8. 已知椭圆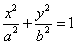 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且
(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且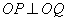 .(1)
.(1)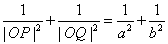 ;(2)|OP|2+|OQ|2的最大值为
;(2)|OP|2+|OQ|2的最大值为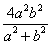 ;(3)
;(3)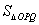 的最小值是
的最小值是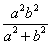 .
.
9. 过椭圆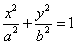 (a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则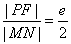 .
.
10. 已知椭圆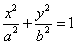 ( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点
( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点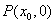 , 则
, 则 .
.
11. 设P点是椭圆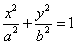 ( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记
( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记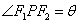 ,则(1)
,则(1)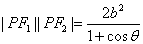 .(2)
.(2) 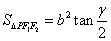 .
.
12. 设A、B是椭圆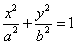 ( a>b>0)的长轴两端点,P是椭圆上的一点,
( a>b>0)的长轴两端点,P是椭圆上的一点,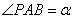 ,
, 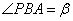 ,
,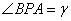 ,c、e分别是椭圆的半焦距离心率,则有(1)
,c、e分别是椭圆的半焦距离心率,则有(1)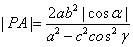 .(2)
.(2) 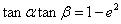 .(3)
.(3) 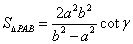 .
.
13. 已知椭圆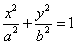 ( a>b>0)的右准线
( a>b>0)的右准线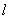 与x轴相交于点
与x轴相交于点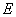 ,过椭圆右焦点
,过椭圆右焦点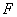 的直线与椭圆相交于A、B两点,点
的直线与椭圆相交于A、B两点,点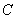 在右准线
在右准线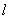 上,且
上,且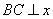 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.)
17. 椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.
18. 椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.
双曲线
1. 双曲线 (a>0,b>0)的两个顶点为
(a>0,b>0)的两个顶点为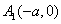 ,
,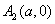 ,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是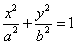 .
.
2. 过双曲线 (a>0,b>o)上任一点
(a>0,b>o)上任一点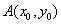 任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且 (常数).
(常数).
3. 若P为双曲线 (a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点,
(a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点,  ,
, 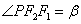 ,则
,则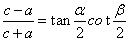 (或
(或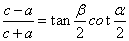 ).
).
4. 设双曲线 (a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记
(a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记 ,
, 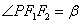 ,
, ,则有
,则有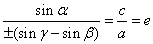 .
.
5. 若双曲线 (a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤
(a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤ 时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为双曲线 (a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则
(a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则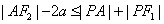 ,当且仅当
,当且仅当 三点共线且
三点共线且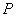 和
和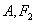 在y轴同侧时,等号成立.
在y轴同侧时,等号成立.
7. 双曲线 (a>0,b>0)与直线
(a>0,b>0)与直线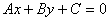 有公共点的充要条件是
有公共点的充要条件是 .
.
8. 已知双曲线 (b>a >0),O为坐标原点,P、Q为双曲线上两动点,且
(b>a >0),O为坐标原点,P、Q为双曲线上两动点,且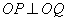 .
.
(1)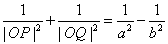 ;(2)|OP|2+|OQ|2的最小值为
;(2)|OP|2+|OQ|2的最小值为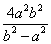 ;(3)
;(3)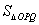 的最小值是
的最小值是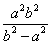 .
.
9. 过双曲线 (a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则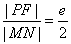 .
.
10. 已知双曲线 (a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点
(a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点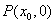 , 则
, 则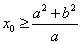 或
或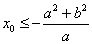 .
.
11. 设P点是双曲线 (a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记
(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记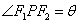 ,则(1)
,则(1)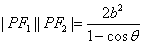 .(2)
.(2) 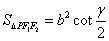 .
.
12. 设A、B是双曲线 (a>0,b>0)的长轴两端点,P是双曲线上的一点,
(a>0,b>0)的长轴两端点,P是双曲线上的一点,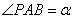 ,
, 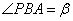 ,
,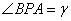 ,c、e分别是双曲线的半焦距离心率,则有(1)
,c、e分别是双曲线的半焦距离心率,则有(1) .
.
(2) 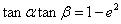 .(3)
.(3) 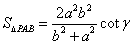 .
.
13. 已知双曲线 (a>0,b>0)的右准线
(a>0,b>0)的右准线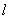 与x轴相交于点
与x轴相交于点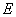 ,过双曲线右焦点
,过双曲线右焦点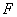 的直线与双曲线相交于A、B两点,点
的直线与双曲线相交于A、B两点,点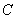 在右准线
在右准线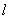 上,且
上,且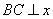 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点).
17. 双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.
双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项
第二篇:解圆锥曲线问题常用方法+椭圆与双曲线的经典结论+椭圆与双曲线的对偶性质总结
解圆锥曲线问题常用方法+椭圆与双曲线的经典结论+椭圆与双曲线的对偶性质总结
解圆锥曲线问题常用以下方法:
1、定义法
(1)椭圆有两种定义。第一定义中,r1+r2=2a。第二定义中,r1=ed1 r2=ed2。
(2)双曲线有两种定义。第一定义中,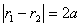 ,当r1>r2时,注意r2的最小值为c-a:第二定义中,r1=ed1,r2=ed2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
,当r1>r2时,注意r2的最小值为c-a:第二定义中,r1=ed1,r2=ed2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
(3)抛物线只有一种定义,而此定义的作用较椭圆、双曲线更大,很多抛物线问题用定义解决更直接简明。
2、韦达定理法
因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用。
3、解析几何的运算中,常设一些量而并不解解出这些量,利用这些量过渡使问题得以解决,这种方法称为“设而不求法”。设而不求法对于直线与圆锥曲线相交而产生的弦中点问题,常用“点差法”,即设弦的两个端点A(x1,y1),B(x2,y2),弦AB中点为M(x0,y0),将点A、B坐标代入圆锥曲线方程,作差后,产生弦中点与弦斜率的关系,这是一种常见的“设而不求”法,具体有:
(1)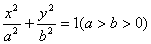 与直线相交于A、B,设弦AB中点为M(x0,y0),则有
与直线相交于A、B,设弦AB中点为M(x0,y0),则有 。
。
(2)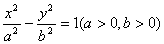 与直线l相交于A、B,设弦AB中点为M(x0,y0)则有
与直线l相交于A、B,设弦AB中点为M(x0,y0)则有
(3)y2=2px(p>0)与直线l相交于A、B设弦AB中点为M(x0,y0),则有2y0k=2p,即y0k=p.
【典型例题】
例1、(1)抛物线C:y2=4x上一点P到点A(3,4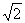 )与到准线的距离和最小,则点 P的坐标为______________
)与到准线的距离和最小,则点 P的坐标为______________
(2)抛物线C: y2=4x上一点Q到点B(4,1)与到焦点F的距离和最小,则点Q的坐标为 。
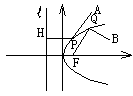 分析:(1)A在抛物线外,如图,连PF,则
分析:(1)A在抛物线外,如图,连PF,则 ,因而易发现,当A、P、F三点共线时,距离和最小。
,因而易发现,当A、P、F三点共线时,距离和最小。
(2)B在抛物线内,如图,作QR⊥l交于R,则当B、Q、R三点共线时,距离和最小。
解:(1)(2,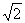 )
)
连PF,当A、P、F三点共线时,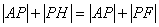 最小,此时AF的方程为
最小,此时AF的方程为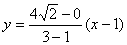 即 y=2
即 y=2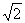 (x-1),代入y2=4x得P(2,2
(x-1),代入y2=4x得P(2,2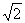 ),(注:另一交点为(
),(注:另一交点为(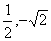 ),它为直线AF与抛物线的另一交点,舍去)
),它为直线AF与抛物线的另一交点,舍去)
(2)(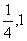 )
)
过Q作QR⊥l交于R,当B、Q、R三点共线时, 最小,此时Q点的纵坐标为1,代入y2=4x得x=
最小,此时Q点的纵坐标为1,代入y2=4x得x= ,∴Q(
,∴Q(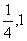 )
)
点评:这是利用定义将“点点距离”与“点线距离”互相转化的一个典型例题,请仔细体会。
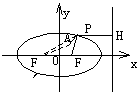 例2、F是椭圆
例2、F是椭圆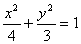 的右焦点,A(1,1)为椭圆内一定点,P为椭圆上一动点。
的右焦点,A(1,1)为椭圆内一定点,P为椭圆上一动点。
(1)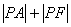 的最小值为
的最小值为
(2)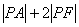 的最小值为
的最小值为
分析:PF为椭圆的一个焦半径,常需将另一焦半径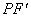 或准线作出来考虑问题。
或准线作出来考虑问题。
解:(1)4-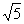
设另一焦点为 ,则
,则 (-1,0)连A
(-1,0)连A ,P
,P

当P是 A的延长线与椭圆的交点时,
A的延长线与椭圆的交点时, 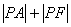 取得最小值为4-
取得最小值为4-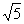 。
。
(2)3
作出右准线l,作PH⊥l交于H,因a2=4,b2=3,c2=1, a=2,c=1,e=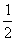 ,
,
∴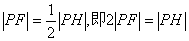
∴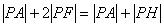
当A、P、H三点共线时,其和最小,最小值为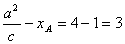
例3、动圆M与圆C1:(x+1)2+y2=36内切,与圆C2:(x-1)2+y2=4外切,求圆心M的轨迹方程。
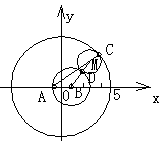 分析:作图时,要注意相切时的“图形特征”:两个圆心与切点这三点共线(如图中的A、M、C共线,B、D、M共线)。列式的主要途径是动圆的“半径等于半径”(如图中的
分析:作图时,要注意相切时的“图形特征”:两个圆心与切点这三点共线(如图中的A、M、C共线,B、D、M共线)。列式的主要途径是动圆的“半径等于半径”(如图中的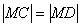 )。
)。
解:如图,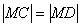 ,
,
∴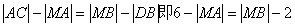
∴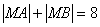 (*)
(*)
∴点M的轨迹为椭圆,2a=8,a=4,c=1,b2=15轨迹方程为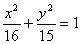
点评:得到方程(*)后,应直接利用椭圆的定义写出方程,而无需再用距离公式列式求解,即列出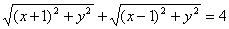 ,再移项,平方,…相当于将椭圆标准方程推导了一遍,较繁琐!
,再移项,平方,…相当于将椭圆标准方程推导了一遍,较繁琐!
例4、△ABC中,B(-5,0),C(5,0),且sinC-sinB=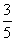 sinA,求点A的轨迹方程。
sinA,求点A的轨迹方程。
分析:由于sinA、sinB、sinC的关系为一次齐次式,两边乘以2R(R为外接圆半径),可转化为边长的关系。
解:sinC-sinB=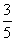 sinA 2RsinC-2RsinB=
sinA 2RsinC-2RsinB=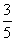 ·2RsinA
·2RsinA
∴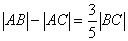
即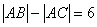 (*)
(*)
∴点A的轨迹为双曲线的右支(去掉顶点)
∵2a=6,2c=10
∴a=3, c=5, b=4
所求轨迹方程为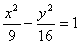 (x>3)
(x>3)
点评:要注意利用定义直接解题,这里由(*)式直接用定义说明了轨迹(双曲线右支)
例5、定长为3的线段AB的两个端点在y=x2上移动,AB中点为M,求点M到x轴的最短距离。
分析:(1)可直接利用抛物线设点,如设A(x1,x12),B(x2,X22),又设AB中点为M(x0y0)用弦长公式及中点公式得出y0关于x0的函数表达式,再用函数思想求出最短距离。
(2)M到x轴的距离是一种“点线距离”,可先考虑M到准线的距离,想到用定义法。
解法一:设A(x1,x12),B(x2,x22),AB中点M(x0,y0)
 则
则

由①得(x1-x2)2[1+(x1+x2)2]=9
即[(x1+x2)2-4x1x2]·[1+(x1+x2)2]=9 ④
由②、③得2x1x2=(2x0)2-2y0=4x02-2y0
代入④得 [(2x0)2-(8x02-4y0)]·[1+(2x0)2]=9
∴ ,
,
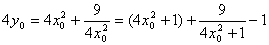
≥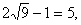
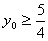
当4x02+1=3 即 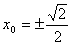 时,
时,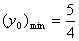 此时
此时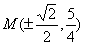
法二:如图,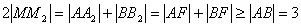
 ∴
∴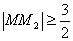 , 即
, 即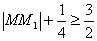 ,
,
∴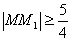 , 当AB经过焦点F时取得最小值。
, 当AB经过焦点F时取得最小值。
∴M到x轴的最短距离为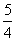
点评:解法一是列出方程组,利用整体消元思想消x1,x2,从而形成y0关于x0的函数,这是一种“设而不求”的方法。而解法二充分利用了抛物线的定义,巧妙地将中点M到x轴的距离转化为它到准线的距离,再利用梯形的中位线,转化为A、B到准线的距离和,结合定义与三角形中两边之和大于第三边(当三角形“压扁”时,两边之和等于第三边)的属性,简捷地求解出结果的,但此解法中有缺点,即没有验证AB是否能经过焦点F,而且点M的坐标也不能直接得出。
例6、已知椭圆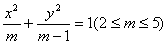 过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D、设f(m)=
过其左焦点且斜率为1的直线与椭圆及准线从左到右依次变于A、B、C、D、设f(m)= ,(1)求f(m),(2)求f(m)的最值。
,(1)求f(m),(2)求f(m)的最值。
分析:此题初看很复杂,对f(m)的结构不知如何运算,因A、B来源于“不同系统”,A在准线上,B在椭圆上,同样C在椭圆上,D在准线上,可见直接求解较繁,将这些线段“投影”到x轴上,立即可得防

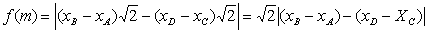

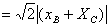
此时问题已明朗化,只需用韦达定理即可。
解:(1)椭圆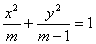 中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
中,a2=m,b2=m-1,c2=1,左焦点F1(-1,0)
则BC:y=x+1,代入椭圆方程即(m-1)x2+my2-m(m-1)=0
得(m-1)x2+m(x+1)2-m2+m=0
∴(2m-1)x2+2mx+2m-m2=0
设B(x1,y1),C(x2,y2),则x1+x2=-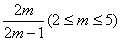
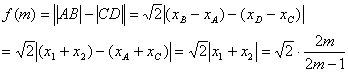
(2)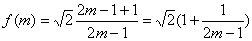
∴当m=5时,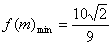
当m=2时,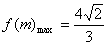
点评:此题因最终需求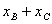 ,而BC斜率已知为1,故可也用“点差法”设BC中点为M(x0,y0),通过将B、C坐标代入作差,得
,而BC斜率已知为1,故可也用“点差法”设BC中点为M(x0,y0),通过将B、C坐标代入作差,得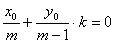 ,将y0=x0+1,k=1代入得
,将y0=x0+1,k=1代入得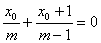 ,∴
,∴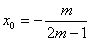 ,可见
,可见
当然,解本题的关键在于对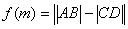 的认识,通过线段在x轴的“投影”发现
的认识,通过线段在x轴的“投影”发现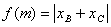 是解此题的要点。
是解此题的要点。
【同步练习】
1、已知:F1,F2是双曲线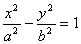 的左、右焦点,过F1作直线交双曲线左支于点A、B,若
的左、右焦点,过F1作直线交双曲线左支于点A、B,若 ,△ABF2的周长为( )
,△ABF2的周长为( )
A、4a B、4a+m C、4a+2m D、4a-m
2、若点P到点F(4,0)的距离比它到直线x+5=0的距离小1,则P点的轨迹方程是
( )
A、y2=-16x B、y2=-32x C、y2=16x D、y2=32x
3、已知△ABC的三边AB、BC、AC的长依次成等差数列,且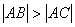 ,点B、C的坐标分别为(-1,0),(1,0),则顶点A的轨迹方程是( )
,点B、C的坐标分别为(-1,0),(1,0),则顶点A的轨迹方程是( )
A、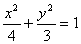 B、
B、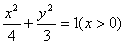
C、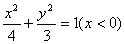 D、
D、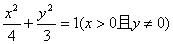
4、过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则椭圆中心的轨迹方程是
( )
A、 B、
B、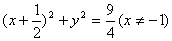
C、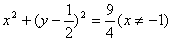 D、
D、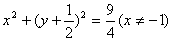
5、已知双曲线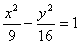 上一点M的横坐标为4,则点M到左焦点的距离是
上一点M的横坐标为4,则点M到左焦点的距离是
6、抛物线y=2x2截一组斜率为2的平行直线,所得弦中点的轨迹方程是
7、已知抛物线y2=2x的弦AB所在直线过定点p(-2,0),则弦AB中点的轨迹方程是
8、过双曲线x2-y2=4的焦点且平行于虚轴的弦长为
9、直线y=kx+1与双曲线x2-y2=1的交点个数只有一个,则k=
10、设点P是椭圆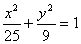 上的动点,F1,F2是椭圆的两个焦点,求sin∠F1PF2的最大值。
上的动点,F1,F2是椭圆的两个焦点,求sin∠F1PF2的最大值。
11、已知椭圆的中心在原点,焦点在x轴上,左焦点到坐标原点、右焦点、右准线的距离依次成等差数列,若直线l与此椭圆相交于A、B两点,且AB中点M为(-2,1),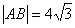 ,求直线l的方程和椭圆方程。
,求直线l的方程和椭圆方程。
12、已知直线l和双曲线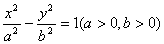 及其渐近线的交点从左到右依次为A、B、C、D。求证:
及其渐近线的交点从左到右依次为A、B、C、D。求证: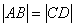 。
。
【参考答案】
1、C
 ,
,
∴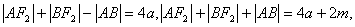 选C
选C
2、C
点P到F与到x+4=0等距离,P点轨迹为抛物线 p=8开口向右,则方程为y2=16x,选C
3、D
∵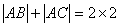 ,且
,且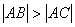
∵点A的轨迹为椭圆在y轴右方的部分、又A、B、C三点不共线,即y≠0,故选D。
4、A
设中心为(x,y),则另一焦点为(2x-1,2y),则原点到两焦点距离和为4得 ,∴
,∴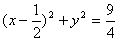
①又c<a,∴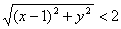
∴(x-1)2+y2<4 ②,由①,②得x≠-1,选A
5、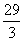
左准线为x=-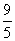 ,M到左准线距离为
,M到左准线距离为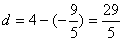 则M到左焦点的距离为
则M到左焦点的距离为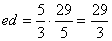
6、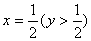
设弦为AB,A(x1,y1),B(x2,y2)AB中点为(x,y),则y1=2x12,y2=2x22,y1-y2=2(x12-x22)
∴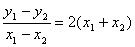 ∴2=2·2x,
∴2=2·2x,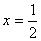
将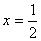 代入y=2x2得
代入y=2x2得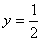 ,轨迹方程是
,轨迹方程是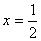 (y>
(y>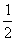 )
)
7、y2=x+2(x>2)
设A(x1,y1),B(x2,y2),AB中点M(x,y),则

∵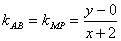 ,∴
,∴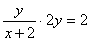 ,即y2=x+2
,即y2=x+2
又弦中点在已知抛物线内P,即y2<2x,即x+2<2x,∴x>2
8、4
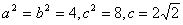 ,令
,令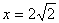 代入方程得8-y2=4
代入方程得8-y2=4
∴y2=4,y=±2,弦长为4
9、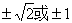
y=kx+1代入x2-y2=1得x2-(kx+1)2-1=0
∴(1-k2)x2-2kx-2=0
①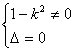 得4k2+8(1-k2)=0,k=
得4k2+8(1-k2)=0,k=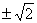
②1-k2=0得k=±1
 10、解:a2=25,b2=9,c2=16
10、解:a2=25,b2=9,c2=16
 设F
1、F
2为左、右焦点,则F
1(-4,0)F
2(4,0)
设F
1、F
2为左、右焦点,则F
1(-4,0)F
2(4,0)
设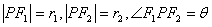
则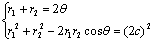
①2-②得2r1r2(1+cosθ)=4b2
∴1+cosθ=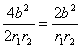 ∵r1+r2
∵r1+r2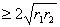 , ∴r1r2的最大值为a2
, ∴r1r2的最大值为a2
∴1+cosθ的最小值为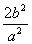 ,即1+cosθ
,即1+cosθ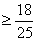
cosθ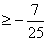 ,
, 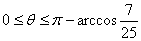 则当
则当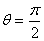 时,sinθ取值得最大值1,
时,sinθ取值得最大值1,
即sin∠F1PF2的最大值为1。
11、设椭圆方程为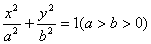
由题意:C、2C、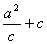 成等差数列,
成等差数列,
∴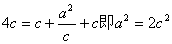 ,
,
∴a2=2(a2-b22DDFFF2+2222222大案要案 000),∴a2=2b2
椭圆方程为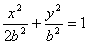 ,设A(x1,y1),B(x2,y2)
,设A(x1,y1),B(x2,y2)
则 ①
① 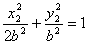 ②
②
①-②得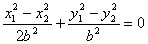
2222222∴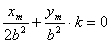
即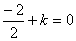 ∴k=1
∴k=1
直线AB方程为y-1=x+2即y=x+3, 代入椭圆方程即x2+2y2-2b2=0得x2+2(x+3)2-2b2=0
∴3x2+12x+18-2b2=0, 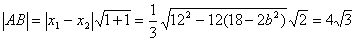
解得b2=12, ∴椭圆方程为 ,直线l方程为x-y+3=0
,直线l方程为x-y+3=0
12、证明:设A(x1,y1),D(x2,y2),AD中点为M(x0,y0)直线l的斜率为k,则

 ①-②得
①-②得
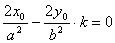 ③
③
设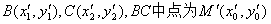 ,
,
 则
则

④-⑤得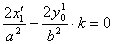 ⑥
⑥
由③、⑥知M、 均在直线
均在直线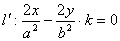 上,而M、
上,而M、 又在直线l上 ,
又在直线l上 ,
若l过原点,则B、C重合于原点,命题成立
若l与x轴垂直,则由对称性知命题成立
若l不过原点且与x轴不垂直,则M与 重合
重合
∴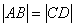
椭圆与双曲线的对偶性质总结
椭 圆
1. 点P处的切线PT平分△PF1F2在点P处的外角.
2. PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相离.
4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.
5. 若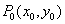 在椭圆
在椭圆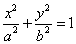 上,则过
上,则过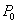 的椭圆的切线方程是
的椭圆的切线方程是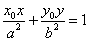 .
.
6. 若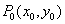 在椭圆
在椭圆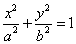 外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
外 ,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是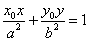 .
.
7. 椭圆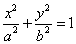 (a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点
(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点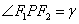 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为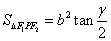 .
.
8. 椭圆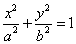 (a>b>0)的焦半径公式:
(a>b>0)的焦半径公式:
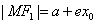 ,
,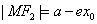 (
(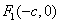 ,
, 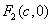
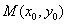 ).
).
9. 设过椭圆焦点F作直线与椭圆相交 P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.
10. 过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是椭圆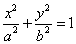 的不平行于对称轴的弦,M
的不平行于对称轴的弦,M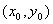 为AB的中点,则
为AB的中点,则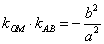 ,
,
即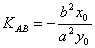 。
。
12. 若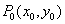 在椭圆
在椭圆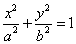 内,则被Po所平分的中点弦的方程是
内,则被Po所平分的中点弦的方程是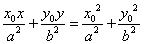 .
.
13. 若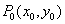 在椭圆
在椭圆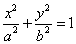 内,则过Po的弦中点的轨迹方程是
内,则过Po的弦中点的轨迹方程是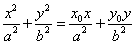 .
.
双曲线
1. 点P处的切线PT平分△PF1F2在点P处的内角.
2. PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3. 以焦点弦PQ为直径的圆必与对应准线相交.
4. 以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)
5. 若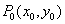 在双曲线
在双曲线 (a>0,b>0)上,则过
(a>0,b>0)上,则过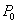 的双曲线的切线方程是
的双曲线的切线方程是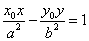 .
.
6. 若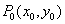 在双曲线
在双曲线 (a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是
(a>0,b>0)外 ,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是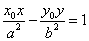 .
.
7. 双曲线 (a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点
(a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点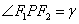 ,则双曲线的焦点角形的面积为
,则双曲线的焦点角形的面积为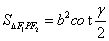 .
.
8. 双曲线 (a>0,b>o)的焦半径公式:(
(a>0,b>o)的焦半径公式:(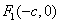 ,
, 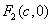
当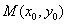 在右支上时,
在右支上时,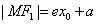 ,
,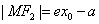 .
.
当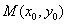 在左支上时,
在左支上时, ,
,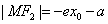
9. 设过双曲线焦点F作直线与双曲线相交 P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.
10. 过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11. AB是双曲线 (a>0,b>0)的不平行于对称轴的弦,M
(a>0,b>0)的不平行于对称轴的弦,M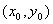 为AB的中点,则
为AB的中点,则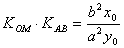 ,即
,即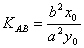 。
。
12. 若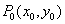 在双曲线
在双曲线 (a>0,b>0)内,则被Po所平分的中点弦的方程是
(a>0,b>0)内,则被Po所平分的中点弦的方程是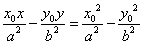 .
.
13. 若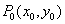 在双曲线
在双曲线 (a>0,b>0)内,则过Po的弦中点的轨迹方程是
(a>0,b>0)内,则过Po的弦中点的轨迹方程是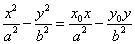 .
.
椭圆与双曲线的经典结论
椭 圆
1. 椭圆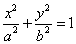 (a>b>o)的两个顶点为
(a>b>o)的两个顶点为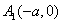 ,
,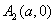 ,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是 .
.
2. 过椭圆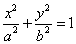 (a>0, b>0)上任一点
(a>0, b>0)上任一点 任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且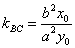 (常数).
(常数).
3. 若P为椭圆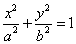 (a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,
(a>b>0)上异于长轴端点的任一点,F1, F 2是焦点, 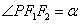 ,
, 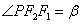 ,则
,则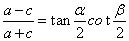 .
.
4. 设椭圆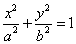 (a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记
(a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记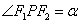 ,
,  ,
,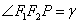 ,则有
,则有 .
.
5. 若椭圆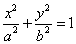 (a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤
(a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤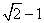 时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为椭圆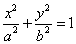 (a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则
(a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则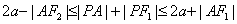 ,当且仅当
,当且仅当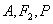 三点共线时,等号成立.
三点共线时,等号成立.
7. 椭圆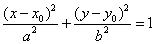 与直线
与直线 有公共点的充要条件是
有公共点的充要条件是 .
.
8. 已知椭圆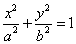 (a>b>0),O为坐标原点,P、Q为椭圆上两动点,且
(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且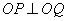 .(1)
.(1)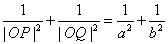 ;(2)|OP|2+|OQ|2的最大值为
;(2)|OP|2+|OQ|2的最大值为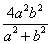 ;(3)
;(3)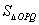 的最小值是
的最小值是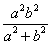 .
.
9. 过椭圆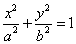 (a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则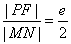 .
.
10. 已知椭圆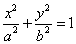 ( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点
( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点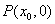 , 则
, 则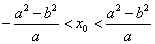 .
.
11. 设P点是椭圆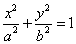 ( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记
( a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记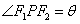 ,则(1)
,则(1)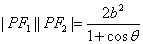 .(2)
.(2) 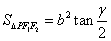 .
.
12. 设A、B是椭圆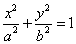 ( a>b>0)的长轴两端点,P是椭圆上的一点,
( a>b>0)的长轴两端点,P是椭圆上的一点,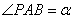 ,
, 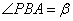 ,
,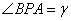 ,c、e分别是椭圆的半焦距离心率,则有(1)
,c、e分别是椭圆的半焦距离心率,则有(1) .(2)
.(2) 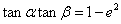 .(3)
.(3) 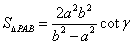 .
.
13. 已知椭圆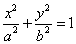 ( a>b>0)的右准线
( a>b>0)的右准线 与x轴相交于点
与x轴相交于点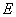 ,过椭圆右焦点
,过椭圆右焦点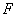 的直线与椭圆相交于A、B两点,点
的直线与椭圆相交于A、B两点,点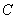 在右准线
在右准线 上,且
上,且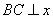 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.)
17. 椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.
18. 椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.
双曲线
1. 双曲线 (a>0,b>0)的两个顶点为
(a>0,b>0)的两个顶点为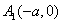 ,
,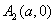 ,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是
,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是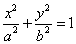 .
.
2. 过双曲线 (a>0,b>o)上任一点
(a>0,b>o)上任一点 任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且
任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且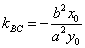 (常数).
(常数).
3. 若P为双曲线 (a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点,
(a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点, 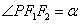 ,
, 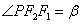 ,则
,则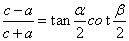 (或
(或 ).
).
4. 设双曲线 (a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记
(a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记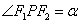 ,
,  ,
,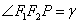 ,则有
,则有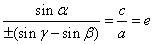 .
.
5. 若双曲线 (a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤
(a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤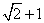 时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6. P为双曲线 (a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则
(a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则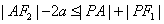 ,当且仅当
,当且仅当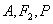 三点共线且
三点共线且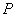 和
和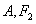 在y轴同侧时,等号成立.
在y轴同侧时,等号成立.
7. 双曲线 (a>0,b>0)与直线
(a>0,b>0)与直线 有公共点的充要条件是
有公共点的充要条件是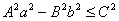 .
.
8. 已知双曲线 (b>a >0),O为坐标原点,P、Q为双曲线上两动点,且
(b>a >0),O为坐标原点,P、Q为双曲线上两动点,且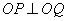 .
.
(1)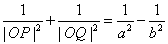 ;(2)|OP|2+|OQ|2的最小值为
;(2)|OP|2+|OQ|2的最小值为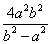 ;(3)
;(3)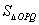 的最小值是
的最小值是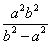 .
.
9. 过双曲线 (a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则
(a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则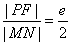 .
.
10. 已知双曲线 (a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点
(a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点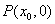 , 则
, 则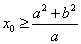 或
或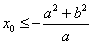 .
.
11. 设P点是双曲线 (a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记
(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记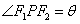 ,则(1)
,则(1)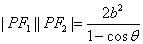 .(2)
.(2) 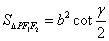 .
.
12. 设A、B是双曲线 (a>0,b>0)的长轴两端点,P是双曲线上的一点,
(a>0,b>0)的长轴两端点,P是双曲线上的一点,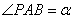 ,
, 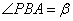 ,
,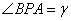 ,c、e分别是双曲线的半焦距离心率,则有(1)
,c、e分别是双曲线的半焦距离心率,则有(1)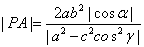 .
.
(2) 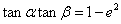 .(3)
.(3) 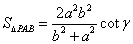 .
.
13. 已知双曲线 (a>0,b>0)的右准线
(a>0,b>0)的右准线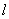 与x轴相交于点
与x轴相交于点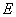 ,过双曲线右焦点
,过双曲线右焦点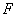 的直线与双曲线相交于A、B两点,点
的直线与双曲线相交于A、B两点,点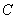 在右准线
在右准线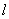 上,且
上,且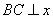 轴,则直线AC经过线段EF 的中点.
轴,则直线AC经过线段EF 的中点.
14. 过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15. 过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点).
17. 双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.
18. 双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.
