高三复数专题复习:
一、复数的概念及运算:
1、复数的概念:(1)虚数单位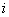 ;
;
(2)实部: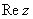 ,虚部:
,虚部: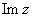 ;
;
(3)复数的分类(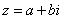 )
) ;
;
(4)相等的复数:
2、复数的加、减、乘、除法则:
(1)加减法具有交换律和结合律;
(2)乘法具有交换律、结合律、分配律;
(3)除法: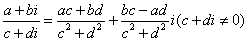 。
。
3、复数的共轭与模:
(1)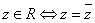 ;
;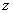 是纯虚数
是纯虚数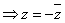 ,反之不成立;
,反之不成立;
(2)复数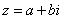 与点
与点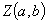 是一一对应关系,另:
是一一对应关系,另: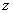 与
与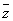 关于
关于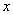 轴对称,
轴对称,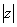 表示
表示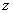 对应点与原点的距离。
对应点与原点的距离。
4、复数共轭运算性质: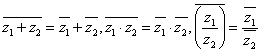 ;
;
5、复数模的运算性质: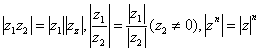 。
。
6、复数的模与共轭的练习: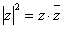 。
。
7、重要结论
(1) 对复数z 、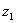 、
、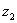 和自然数m、n,有
和自然数m、n,有
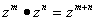 ,
,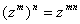 ,
,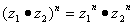
(2) 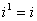 ,
,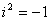 ,
,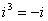 ,
,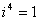 ;
;
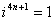 ,
,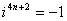 ,
,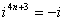 ,
,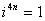 .
.
(3) 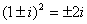 ,
,
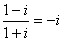 ,
,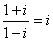 .
.
(4)设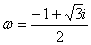 ,
,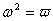 ,
,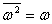 ,
,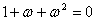 ,
,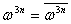 ,
,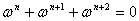
8.一些几何结论的复数形式

二、复数的三角形式:
1、复数的三角形式概念:
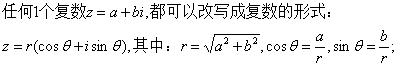
2、复数的三角形式的乘法公式:
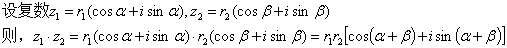
即:两个复数相乘,积的模等于两个复数的模之积,积的辐角等于两个复数的辐角之和。

3、复数的三角形式的乘方公式(棣莫佛定理)
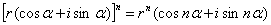
即:复数的n(n∈N)次幂的模等于模的n次幂,辐角等于这个复数的辐角的n倍,这个定理称为棣莫佛定理。
4、复数的三角形式的除法公式
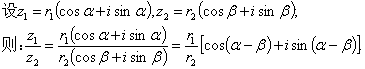
即:两个复数像除,商的模等于被除数的模除以除数的模,商的辐角等于被除数的辐角减去除数的辐角。
三、复数中的方程问题:
1、实系数一元二次方程的根的情况:
对方程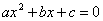 (其中
(其中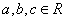 且
且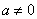 ),令
),令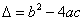 ,
,
当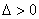 时,方程有两个不相等的实数根。
时,方程有两个不相等的实数根。
当 =0时,方程有两个相等的实根;
=0时,方程有两个相等的实根;
当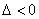 时,方程有两个共轭虚根:
时,方程有两个共轭虚根: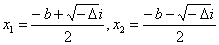 。
。
2、复系数一元二次方程根的情况:
对方程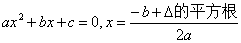 ;
;
3、一元二次方程的根与系数的关系:
若方程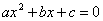 (其中
(其中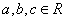 且
且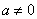 )的两个根为
)的两个根为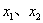 ,则
,则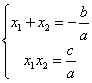 ;
;
四、例题精选
例1:已知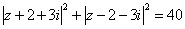 ,求
,求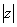 ;
;
例2:已知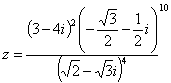 ,求
,求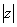 ;
;
例3:设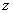 为虚数,
为虚数,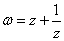 为实数,且
为实数,且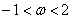 。
。
(1)求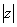 的值及
的值及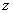 的实部的取值范围;
的实部的取值范围;
(2)证明: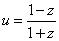 为纯虚数;
为纯虚数;
例4:已知关于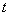 的方程
的方程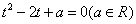 有两个根
有两个根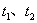 ,且满足
,且满足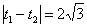 。
。
(1)求方程的两个根以及实数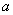 的值;
的值;
(2)当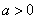 时,若对于任意
时,若对于任意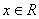 ,不等式
,不等式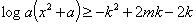 对于任意的
对于任意的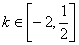 恒成立,求实数
恒成立,求实数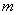 的取值范围。
的取值范围。
例5:已知复数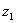 满足
满足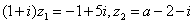 ,其中
,其中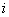 为虚数单位,
为虚数单位,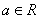 ,若
,若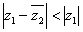 ,求
,求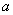 的取值范围。
的取值范围。
例6:设虚数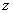 满足
满足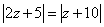 。
。
(1)求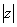 的值;
的值;
(2)若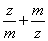 为实数,求实数
为实数,求实数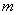 的值;
的值;
(3)若 在复平面上对应的点在第一、第三象限角平方线上,求复数
在复平面上对应的点在第一、第三象限角平方线上,求复数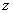 。
。
例7:已知方程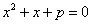 有两个根
有两个根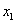 和
和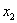 ,
,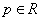 。
。
(1)若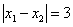 ,求实数
,求实数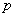 ;
;
(2)若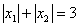 ,求实数
,求实数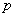 ;
;
例8:已知复数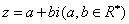 是方程
是方程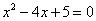 的根,复数
的根,复数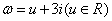 满足
满足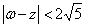 ,求
,求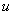 的取值范围。
的取值范围。
例9:关于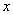 的方程
的方程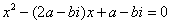 有实根,求一个根的模是2,求实数
有实根,求一个根的模是2,求实数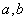 的值。
的值。
例10:设两复数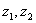 满足
满足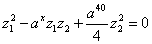 (其中
(其中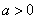 且
且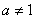 ,
,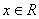 ),求
),求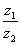 是虚数。
是虚数。
(1)求证: 是定值,求出此定值;
是定值,求出此定值;
(2)当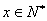 时,求满足条件的虚数
时,求满足条件的虚数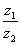 的实部的所有项的和。
的实部的所有项的和。
例11:设两个复数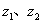 满足
满足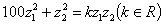 ,并且
,并且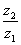 是虚数,当
是虚数,当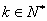 时,求所以满足条件的虚数
时,求所以满足条件的虚数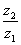 的实部之和。
的实部之和。
例12:计算:(1)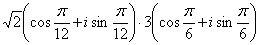
(2)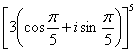
(3)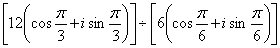
例13:给定复数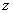 ,在
,在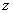 ,
,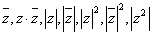 这八个值中,不同值的个数至多是___________。
这八个值中,不同值的个数至多是___________。
例14:已知下列命题
(1)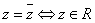 ;(2)
;(2)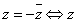 为纯虚数;(3)
为纯虚数;(3)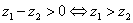 ;
;
(4)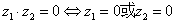 ;(5)
;(5) ;(6)
;(6)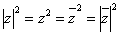 .
.
其中正确的命题是____________;
例15:是否存在复数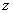 同时满足条件:①
同时满足条件:①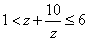 ;②
;②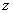 的实部、虚部为整数。若存在,求出复数
的实部、虚部为整数。若存在,求出复数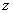 ,若不存在,说明理由。
,若不存在,说明理由。
例16:设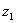 是已知复数,
是已知复数,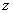 为任意复数且
为任意复数且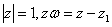 ,则复数
,则复数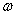 对应的点的轨迹是( )
对应的点的轨迹是( )
A、以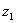 的对应点为圆心、1为半径的圆;
的对应点为圆心、1为半径的圆;
B、以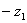 的对应点为圆心,1为半径的圆;
的对应点为圆心,1为半径的圆;
C、以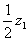 的对应点为圆心、
的对应点为圆心、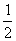 为半径的圆;
为半径的圆;
D、以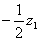 的对应点为圆心,
的对应点为圆心,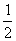 为半径的圆;
为半径的圆;
例17:满足方程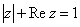 的复数
的复数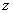 对应的点的轨迹是 ( )。
对应的点的轨迹是 ( )。
A、圆 B、椭圆 C、双曲线 D、抛物线
例18:复平面内,满足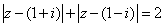 的复数
的复数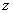 所对应的点的轨迹是 ( )
所对应的点的轨迹是 ( )
A、椭圆 B、双曲线 C、一条线段 D、不存在
例19:满足方程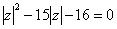 的复数
的复数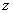 对应的点的轨迹是 ( )
对应的点的轨迹是 ( )
A、四个点 B、四条直线 C、一个圆 D、两个圆
例20:设复数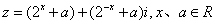 ,当
,当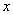 在
在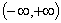 内变化时,求
内变化时,求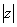 的最小值
的最小值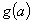 。
。
例21:若复数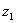 和
和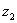 满足:
满足: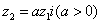 ,且
,且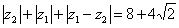 。
。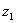 和
和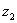 在复平面中对应的点为
在复平面中对应的点为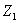 和
和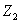 ,坐标原点为O,且
,坐标原点为O,且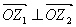 ,求
,求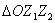 面积的最大值,并指出此时
面积的最大值,并指出此时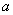 的值。
的值。
例22:已知复数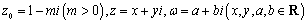 ,i为虚数单位,且对于任意复数
,i为虚数单位,且对于任意复数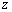 ,有
,有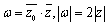 。
。
(1)试求m的值,并分别写出a和b用x、y表示的关系式;
(2)将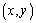 作为点P的坐标,
作为点P的坐标,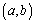 作为点Q的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点P变到这一平面上的点Q,当点P在直线
作为点Q的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点P变到这一平面上的点Q,当点P在直线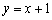 上移动时,试求点P经该变换后得到的点Q的轨迹方程;
上移动时,试求点P经该变换后得到的点Q的轨迹方程;
(3)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。
例23:已知复数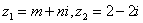 和
和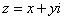 ,其中
,其中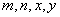 均为实数,且
均为实数,且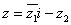 。
。
(1)若复数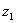 所对应的点
所对应的点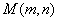 在曲线
在曲线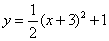 上运动,求复数
上运动,求复数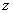 所对应的点
所对应的点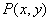 的轨迹方程;
的轨迹方程;
(2)将(1)中点P的轨迹上每一点沿向量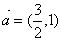 方向平移,得到新的轨迹C,求C的方程。
方向平移,得到新的轨迹C,求C的方程。
(3)轨迹C上任意一点A(异于顶点)作其切线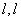 交
交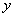 轴于点B。问:以
轴于点B。问:以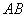 为直径的圆是否恒过
为直径的圆是否恒过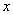 轴上一定点?若存在,求出此定点坐标;若不存在,则说明理由。
轴上一定点?若存在,求出此定点坐标;若不存在,则说明理由。
例题答案:
1、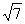 ;2、1; 3、(1)
;2、1; 3、(1)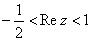 ;(2)略;5、
;(2)略;5、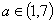 ;6、(1)
;6、(1)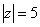 ;(2)
;(2)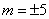 ;(3)
;(3)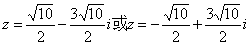 ;7、(1)
;7、(1)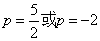 ;(2)①当
;(2)①当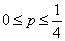 时,方程无解;②当
时,方程无解;②当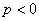 时,
时,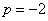 ;③当
;③当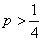 时,
时,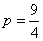 ;8、
;8、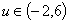 ;9、当
;9、当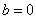 时,
时,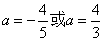 ;当
;当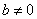 时,
时,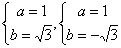 。
。
10、(1)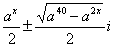 ,定值
,定值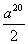 ;(2)
;(2)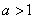 时,
时,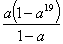 ;
;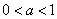 时,
时,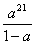 ;
;
11、95;12、略;13、4; 14、(1)(4);15、存在、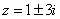 或
或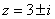 ;
;
16、D;17、D;18、C;19、C;
20、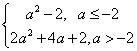 ;21、8,此时
;21、8,此时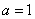 ,提示:由条件得
,提示:由条件得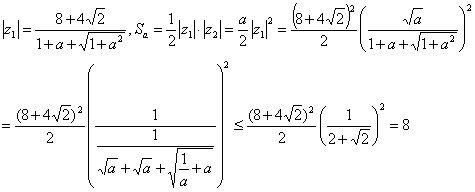 ,
,
当且仅当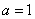 时等号成立。
时等号成立。
22、(1)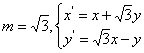 ;(2)
;(2)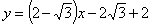 ;(3)存在直线
;(3)存在直线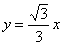 ,
,
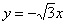 ;
;
提示:设存在直线满足条件,由条件该直线不能平行与坐标轴,设方程为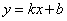 ,则变换后的直线为
,则变换后的直线为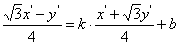 ,即
,即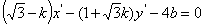 。它与
。它与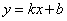 重合,当
重合,当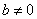 时,方程无解。当
时,方程无解。当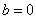 时,
时,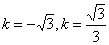 ;
;
第二篇:江苏省高三一轮数学复习专题材料专题9_复数
专题9 复数
江苏省太仓高级中学 钱华
【课标要求】
1.课程目标
回顾数系的扩充过程,体会数的概念是逐步发展起来的,了解引进复数的必要性,感悟数的概念产生于实际需求与数学的内部矛盾,感受人类理性思维的作用以及数与现实世界的联系.理解复数的概念以及复数的代数表示,掌握复数相等的充要条件.掌握复数代数形式的运算法则,能进行复数代数形式的四则运算.理解复数的几何意义,了解复数代数形式的加、减运算的几何意义.
2.复习要求
(1)复数的概念.掌握复数的分类,明确复数集、实数集、虚数集、纯虚数集之间的关系;掌握复数相等的充要条件;掌握共轭复数、复数的模等基本概念;
(2)复数的表示.复数的代数形式,几何表示(复平面内的点和向量),明确复数几何表示的本质,并适当联系解析几何与平面向量;
(3)复数的代数运算.熟练掌握复数代数形式的四则运算.
3.复习建议
(1)复数的复习重点是帮助学生明确复数问题求解的基本方法是“化复为实”,进一步熟练掌握复数的四则运算,能够自觉的运用类比的思想方法掌握复数代数形式的运算法则.
(2)重视复数中的基本概念和性质,在复习的过程中,要设置一些概念性问题,帮助学生理清概念性质,夯实基础.
(3)要向学生强调复数问题求解的基本方法是“化复为实”,即复数问题的解决,最终都是利用两个复数相等的充要条件将复数相等转化为两组实数的相等从而解决问题.
(4)复数的乘法运算中应注意对虚单位“i”的周期性的重视,并引申出“1±i”的高次运算的方法,了解1的三个立方根,ω的高次运算问题.
(5)了解复数的几何意义,并能适度与平面向量及解析几何联系.
【典型例题】
例1.填空题
(1)下列关于复数的说法正确的是 .(填上所有正确命题的序号)
① 任意两个复数都不能比较大小;
② 纯虚数在复平面内的对应点都在虚轴上;
③ 若z是纯虚数,则z≠;
④ 任意复数z,总有|z2|= |z|2.
答案:②③④.
解析:①不正确,两个虚数不能比较大小,但复数集不仅包含虚数集,还包含实数集,若在复数集中取出两个实数,则能够比较大小;②认清虚轴与y轴的区别;③对与任意纯虚数bi(b∈R,b≠0),
若bi=,则b2= -1,因为b∈R,所以矛盾;④因为|z1z2|=|z1||z2|,所以结论正确.
(2)计算: = .
解析: = =2-i.
(3)计算: + =___________.
解析: + = i+(-i)=0.
(4)若复数z=(m2+m-1)+(4m2-8m+3)i (m∈R)的共轭复数对应的点在第一象限,则实数m的取值范围是__________.
答案:<m<
解析:∵z=(m2+m-1)+(4m2-8m+3)i的共轭复数=(m2+m-1)-(4m2-8m+3)i,
∴其对应的点是A(m2+m-1, -4m2+8m-3),
∴,解得:<m<.
(5)已知复数z满足|z|=1且z2= -1,则z=_________.
答案:±i.
解析:设z=x+yi (x,y∈R),由|z|=1得x2+y2=1,又z2=x2-y2+2xyi= -1,
∴,解得.
(6)若复数(x-2)+yi (x,y∈R)的模为,则的最大值为 .
答案:.
解:因为(x-2)+yi (x,y∈R)的模为=,所以(x-1)2+y2=3,由 的几何意义是点(x,y)与原点连线的斜率,所以 ( )max=.
(7)设z1=1+2ai,z2=a-i (a∈R),集合A={z| |z-z1|≤},B={z| |z-z2|≤2},A∩B= ,则a的取值范围是 .
,则a的取值范围是 .
答案:a<-2或a> .
解析:在复平面内,A={z| |z-z1|≤}表示以复数z1对应点为圆心,为半径的圆及其内部;B={z| |z-z2|≤2}表示以复数z2对应点为圆心,2为半径的圆及其内部;∵A∩B= ,两圆外离.则|z1-z2|>3==> (a-1)2+(2a+1)2>18==> 5a2+2a-16>0==>a<-2或a> .
,两圆外离.则|z1-z2|>3==> (a-1)2+(2a+1)2>18==> 5a2+2a-16>0==>a<-2或a> .
(8)已知关于x的方程x2+(1+2i)x-(3m-1)i=0有实数根,则纯虚数m的值是_______.
答案: i.
解析:∵m为纯虚数,∴设m=bi (b∈R),方程的实数根为k.
∴k2+(1+2i)k-(3bi-1)i=(k2+k+3b)+(2k+1)i=0.
∴,解得.
例2.设虚数z满足|z|=1,z2 + 2z+ <0,求z.
解:设z=x+yi (x,y∈R,y≠0),由|z|=1得x2+y2=1,
而z2+2z+ =(x+yi)2 + 2(x+yi) + = (x2-y2+3x)+y(2x+1)i,
又y≠0,∴,解得:,
∴z= - + i.
例3.已知z=1+i,
(1)设w=z2+3 -4,求w;
(2)若 = 1-i,求实数a,b的值.
解:(1)∵z=1+i,
∴w=z2+3 -4 = (1+i)2+3(1-i)-4 = -1-i.
(2)由 = 1-i,把z=1+i代入得: = 1-i,
∴ = 1-i,
∴(a+b)+(a+2)i = (1-i)i = 1+i,
∴,得.
例4.设存在复数z同时满足下列条件:
(1)复数z在复平面内对应的点位于第二象限;
(2)z+2iz=8+ai (a∈R);
求实数a的取值范围.
解:设z=x+yi (x,y∈R),则=x-yi.
由(1)得:x<0,y>0,
又 z+2iz=8+ai,
∴(x+yi)(x-yi)+2i(x+yi)=8+ai 即 (x2+y2-2y)+2xi=8+ai.
∴==>,
∵x2+(y-1)2=9且x<0,
∴-3≤x<0,即-6≤<0,
∴a的取值范围是[-6,0).
例5.已知复数z满足:| z+2-2i |=1,求| z-3-2i |的最小值.
解:(方法一)设设z=x+yi (x,y∈R),
∴| z+2-2i |=|(x+yi)-2-2i|= =1,
即(x+2)2+(y-2)2=1.
∴| z-3-2i |== (-3≤x≤-1).
∴x= -1是,| z-3-2i |min= 4.
(方法二)有复数及其模的几何意义知:满足| z+2-2i |=1即| z-(-2+2i) |=1的复数z所对应的点在以C(-2,2)为圆心,r=1为半径的圆上,而| z-3-2i |=| z-(3+2i) |的几何意义是:复数z对应的点与点A(3,2)的距离,由圆的知识可知| z-3-2i |的最小值为|AC|-r=4.
(方法三)∵| z-3-2i |=|(z+2-2i)-5|≥| | z+2-2i|+|5| |= 4,
∴| z-3-2i |min= 4.
例6.设z是虚数,ω= z+是实数,且-1<ω<2
(Ⅰ)求|z|的值及z的实部的取值范围;
(Ⅱ)设u= ,求证:u为纯虚数;
(Ⅲ)求ω-u2的最小值
解:(Ⅰ)解:设z=a+bi(a、b∈R,b≠0),则ω=a+bi+ = (a+)+(b- )i
∵ω是实数,b≠0,∴a2+b2=1,即|z|=1
∵ω=2a,则-1<ω<2,∴z的实部的取值范围是(- ,1).
(Ⅱ)证明:u= = = = = - i
∵a∈(- ,1),b≠0,∴u为纯虚数
(Ⅲ)解:ω-u2=2a+ =2a+ =2a- =2a-1+=2[(a+1)+]-3
∵a∈(- ,1),∴a+1>0
∴ω-u2≥2×2-3=1
当a+1= ,即a=0时,上式取等号 ∴ω-u2的最小值为1
∴ω-u2的最小值为1
【专题训练】
一、填空题
1.复数(1+mi)(2+i)是纯虚数,则实数m=_______.
2.设集合M={1,2,(a2-3a-1)+(a2-5a-6)i},N={-1,3},若M∩N={3},则实数a= .
3.计算:i+i2+i3+…+i2008= .
4.计算:= .
5.若复数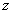 满足 = i,则|1+z|= .
满足 = i,则|1+z|= .
6.已知复数ω= - + i,则下列关于ω的描述正确的是 .(写上所有正确的命题的序号)
①|ω|=1; ②ω2=; ③ω3=1; ④1+ω+ω2=0;
7.已知z∈C,且|z-1|=1,则|z-2i|的取值范围是 .
8.已知复平面内一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,则第四个顶点对应的复数为 .
9.若复数z1,z2满足|z1|=|z2|=2,|z1+z2|=2,则|z1-z2|= .
10.定义复数的一种运算z1※z2=,若复数z=a+bi且实数a,b满足a+b=3,则z ※的最小值为___
二、解答题
11.已知x为实数,y为纯虚数,且满足(2x-1)+(3-y)i=y-i,求x和y.
12.已知z为复数,z+2i、(i为虚数单位)均为实数,且复数(z+ai)2在复平面内对应的点在第一象
限,求实数a的取值范围.
13. 设z∈C,求满足z+∈R且|z-2|=2的复数z.
14.设复数z1=x+yi(x,y∈R,y≠0),复数z2=cosα+isinα(α∈R),且z12+2∈R,z1在复平面内所对应的点在直线y=x上,求|z1-z2|的取值范围.
15.设复数z1,z2满足z1z2+2iz1-2iz2+1=0.
(1)若z1,z2满足 -z1=2i,求z1,z2;
(2)若|z1|=,是否存在常数k,使得等式|z2-4i|=k恒成立?若存在,求出k;若不存在,说明理由.
16.设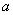 是不等于
是不等于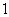 的正实数,
的正实数,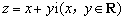 规定
规定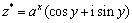 .
.
(1)求证: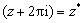 ;
;
(2)设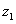 、
、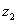 为两个复数,试证明:
为两个复数,试证明: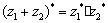 ;
;
(3)类比(2)的结论写出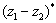 的有关运算式子,并证明你的结论.
的有关运算式子,并证明你的结论.
【复数专题训练参考答案】
1.2; 2.-1 3.0; 4.-16; 5.; 6.①②③④; 7.[-1, +1];
8.-1+3i; 9. 10.
11.解: ∵y为纯虚数,可设y=bi (b∈R,b≠0),则(2x-1)+3i+b=(b-1)i.
整理得: (2x-1+b)+3i=(b-1)i
由复数相等的充要条件得: ,解得.
∴ x= - ,y= 4i.
12.解:设z=x+yi (x,y∈R),由z+2i、均为实数,得z=4-2i.
∴(z+ai)2=[4+(a-2)i]2=16-(a-2)2+8(a-2)i.
∵(z+ai)2在复平面内对应的点在第一象限,
∴16-(a-2)2>0且8(a-2)>0,解得:2<a<6.
13.解:设z=a+bi(a,b∈R),
则z+=a+bi+=a++(b- )i∈R.
∴b=∴b=0或a2+b2=1.
(1)当b=0时,z=a,∴|a-2|=2 ∴a=0或4
a=0不合题意舍去,∴z=4
(2)当b≠0时,a2+b2=1又∵|z-2|=2,∴(a-2)2+b2=4.
解得a= ,b=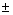 ,∴z= ± i.
,∴z= ± i.
综上,z=4或z= ± i.
14.解:z12+2 ∈R,z1对应的点在直线y=x上,
∴,∴,
∴x=y=1,∴z1=1+i.
∴|z1-z2|==.
∵sin(α+)∈[-1,1],
∴|z1-z2|∈[-1, +1] .
15.解:(1)由=z1+2i,得z2=-2i.
代入已知方程得:z1(-2i)+2iz1-2i(-2i)+1=0.
即|z1|2-2i-3=0,令z1=a+bi (a,b∈R),即可得到(a2+b2-2b-3)-2ai=0,
解得a=0,b=3,或a=0,b= -1,
∴z1=3i,z2= -5i,或z1=z2= -i.
(2)由已知得z1= ,又|z1|=,
∴||=,∴|2iz2-1|2=3|z2+2i|2.
∴(2iz2-1)(-2i-1)=3(z2+2i)( -2i) .整理得:z2+4iz2-4i-11=0.
即(z2-4i)( +4i)=27,∴|z2-4i|2=27,即|z2-4i|=3.
∴存在常数k=3,使得等式|z2-4i|=k恒成立.
16.证明:(1)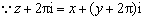 ,
,
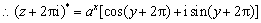
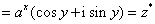 得证;
得证;
(2)设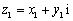 ,
,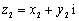 ,
,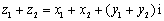 ,
,
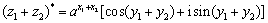 ,
,
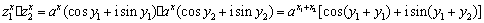
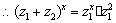 ;
;
(3)类比,得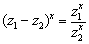 ,
,
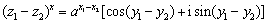 ,
,
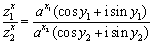
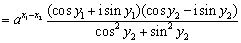
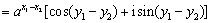 ,
,
原命题得证.
