立体几何空间向量知识点总结
一、共面向量
1、定义
平行于同一平面的向量叫做共面向量.
2、共面向量定理
若两个向量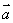 、
、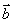 不共线,则向量
不共线,则向量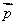 与向量
与向量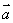 、
、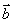 共面的充要条件是存在实数对x、y,使得
共面的充要条件是存在实数对x、y,使得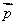 =
= 。
。
3、空间平面的表达式
空间一点P位于平面MAB内的充要条件是存在有序实数对x、y使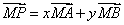 或对空间任一定点O,有
或对空间任一定点O,有
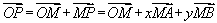 或
或 (其中
(其中 )这几个式子是M,A,B,P四点共面的充要条件.
)这几个式子是M,A,B,P四点共面的充要条件.
二、空间向量基本定理
1、定理
如果三个向量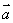 、
、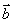 、
、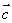 不共面,那么对空间任一向量
不共面,那么对空间任一向量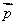 ,存在唯一的有序实数组x、y、z,使
,存在唯一的有序实数组x、y、z,使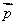 =
=
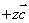
2、注意以下问题
(1)空间任意三个不共面的向量都可以作为空间向量的一个基底.
(2)由于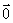 可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是
可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是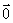 。
。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,两者是相关联的不同概念.
由空间向量的基本定理知,若三个向量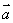 、
、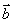 、
、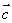 不共面。那么所有空间向量所组成的集合就是
不共面。那么所有空间向量所组成的集合就是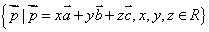 ,这个集合可看做是由向量
,这个集合可看做是由向量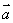 、
、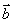 、
、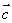 生成的,所以我们把
生成的,所以我们把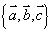 称为空间的一个基底。
称为空间的一个基底。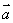 、
、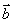 、
、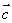 叫做基向量,空间任意三个不共面的向量都可构成空间的一个基底.
叫做基向量,空间任意三个不共面的向量都可构成空间的一个基底.
三、直线方向向量与平面法向量
1、若两直线l1、l2的方向向量分别是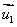 、
、 ,则有l1// l2
,则有l1// l2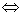
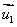 //
//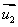 ,l1⊥l2
,l1⊥l2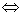
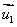 ⊥
⊥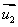 .
.
2、若两平面α、β的法向量分别是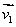 、
、 ,则有α//β
,则有α//β
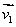 //
//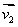 ,α⊥β
,α⊥β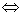
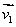 ⊥
⊥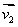 .
.
若直线l的方向向量是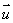 ,平面的法向量是
,平面的法向量是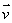 ,则有l//α
,则有l//α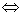
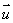 ⊥
⊥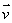 ,l⊥α
,l⊥α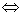
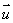 //
//
四、平面法向量的求法
若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:
1、设出平面的法向量为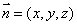 .
.
2、找出(求出)平面内的两个不共线的向量的坐标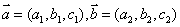
3、根据法向量的定义建立关于x,y,z的方程组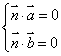
4、解方程组,取其中一个解,即得法向量
五、用向量方法证明空间中的平行关系和垂直关系
(一)用向量方法证明空间中的平行关系
空间中的平行关系主要是指:线线平行、线面平行、面面平行.
1、线线平行
设直线l1、l2的方向向量分别是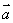 、
、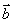 ,则要证明l1// l2,只需证明
,则要证明l1// l2,只需证明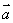 //
//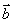 ,即
,即
2、线面平行
(1)设直线l的方向向量是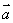 ,平面
,平面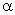 的法向量是
的法向量是 ,则要证明
,则要证明 ,只需证明
,只需证明 ,即
,即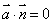 .
.
(2)根据线面平行的判定定理:“如果直线(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可.
(3)根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
3、面面平行
(1)由面面平行的判定定理,要证明面面平行,只要转化为相应的线面平行、线线平行即可.
(2)若能求出平面α、β的法向量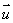 、
、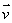 ,则要证明α//β,只需证明
,则要证明α//β,只需证明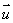 //
// 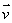
(二)用向量方法证明空间中的垂直关系
空间中的垂直关系主要是指:线线垂直、线面垂直、面面垂直.
1、线线垂直
设直线l1、l2的方向向量分别是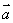 、
、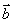 ,则要证明l1⊥ l2,只需证明
,则要证明l1⊥ l2,只需证明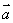 ⊥
⊥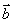 ,即
,即
2、线面垂直
(1)设直线l的方向向量是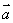 ,平面α的法向量是
,平面α的法向量是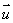 ,则要证l⊥α,只需证明
,则要证l⊥α,只需证明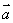 //
// 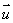
(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直.
3、面面垂直
(1)根据面面垂直的判定定理转化为证相应的线面垂直、线线垂直.
(2)证明两个平面的法向量互相垂直.
六、用向量方法求空间的角
(一)两条异面直线所成的角
1、定义:设a、b是两条异面直线,过空间任一点O作直线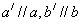 ,则
,则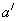 与
与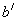 所夹的锐角或直角叫做a与b所成的角.
所夹的锐角或直角叫做a与b所成的角.
2、范围:两异面直线所成角θ的取值范围是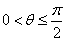
3、向量求法:设直线a、b的方向向量为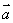 、
、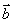 ,其夹角为
,其夹角为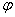 ,则有
,则有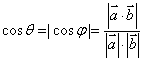
4、注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但两者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
(二)直线与平面所成的角
1、定义:直线和平面所成的角,是指直线与它在这个平面内的射影所成的角.
2、范围:直线和平面所成角θ的取值范围是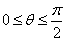
3、向量求法:设直线l的方向向量为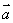 ,平面的法向量为
,平面的法向量为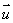 ,直线与平面所成的角为θ,
,直线与平面所成的角为θ,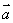 与
与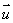 的夹角为
的夹角为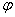 ,则有
,则有
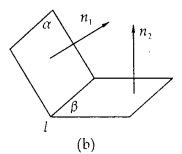
(三)二面角
1、二面角的取值范围: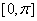
2、二面角的向量求法
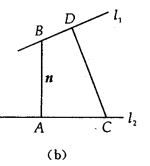
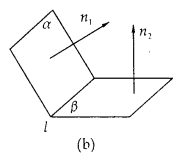
(1)若AB、CD分别是二面角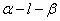 的两个面内与棱l垂直的异面直线,则二面角的大小就是向量
的两个面内与棱l垂直的异面直线,则二面角的大小就是向量 与
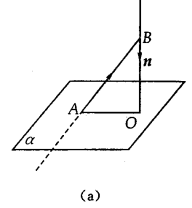
与 的夹角(如图(a)所示).
的夹角(如图(a)所示).
(2)设 、
、 是二面角
是二面角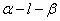 的两个角α、β的法向量,则向量
的两个角α、β的法向量,则向量 与
与 的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).
的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).

七、用向量的方法求空间的距离
(一)点面距离的求法
如图(a)所示,BO⊥平面α,垂足为O,则点B到平面α的距离就是线段BO的长度.若AB是平面α的任一条斜线段,则在Rt△BOA中,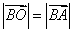 cos∠ABO=
cos∠ABO=
 。如果令平面α的法向量为
。如果令平面α的法向量为 ,考虑到法向量的方向,可以得到B点到平面α的距离为
,考虑到法向量的方向,可以得到B点到平面α的距离为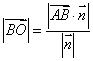 。
。
因此要求一个点到平面的距离,可以分以下几步完成:
1、求出该平面的一个法向量.
2、找出从该点出发的平面的任一条斜线段对应的向量.
3、求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离.
由于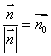 可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即
可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即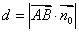 .
.
另外,等积法也是点到面距离的常用求法.
(二)线面距、面面距均可转化为点面距离用求点面距的方法进行求解。
(三)两异面直线距离的求法
如图(b)所示,设l1、l2是两条异面直线, 是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是
是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是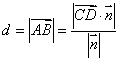 。
。
【典型例题】
例1. 设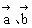 分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
(1) =(2,3,-1),
=(2,3,-1), =(-6,-9,3);
=(-6,-9,3);
(2) =(5,0,2),
=(5,0,2), =(0,4,0);
=(0,4,0);
(3) =(-2,1,4),
=(-2,1,4), =(6,3,3)
=(6,3,3)
例2. 设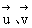 分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
(1)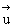 =(1,-1,2),
=(1,-1,2),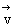 =(3,2,
=(3,2,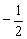 );
);
(2)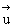 =(0,3,0),
=(0,3,0),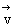 =(0,-5,0);
=(0,-5,0);
(3)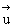 =(2,-3,4),
=(2,-3,4),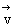 =(4,-2,1)。
=(4,-2,1)。
例3. 已知点A(3,0,0),B(0,4,0),C(0,0,5),求平面ABC的一个单位法向量。
第二篇:空间向量与立体几何知识点
立体几何空间向量知识点总结
知识网络:


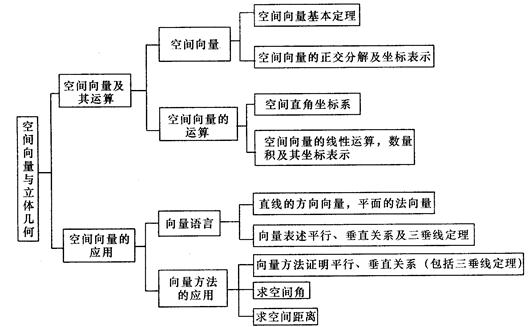
知识点拨:
1、空间向量的概念及其运算与平面向量类似,向量加、减法的平行四边形法则,三角形法则以及相关的运算律仍然成立.空间向量的数量积运算、共线向量定理、共面向量定理都是平面向量在空间中的推广,空间向量基本定理则是向量由二维到三维的推广.
2、当 、
、 为非零向量时.
为非零向量时.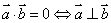 是数形结合的纽带之一,这是运用空间向量研究线线、线面、面面垂直的关键,通常可以与向量的运算法则、有关运算律联系来解决垂直的论证问题.
是数形结合的纽带之一,这是运用空间向量研究线线、线面、面面垂直的关键,通常可以与向量的运算法则、有关运算律联系来解决垂直的论证问题.
3、公式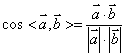 是应用空间向量求空间中各种角的基础,用这个公式可以求两异面直线所成的角(但要注意两异面直线所成角与两向量的夹角在取值范围上的区别),再结合平面的法向量,可以求直线与平面所成的角和二面角等.
是应用空间向量求空间中各种角的基础,用这个公式可以求两异面直线所成的角(但要注意两异面直线所成角与两向量的夹角在取值范围上的区别),再结合平面的法向量,可以求直线与平面所成的角和二面角等.
4、直线的方向向量与平面的法向量是用来描述空间中直线和平面的相对位置的重要概念,通过研究方向向量与法向量之间的关系,可以确定直线与直线、直线与平面、平面与平面等的位置关系以及有关的计算问题.
5、用空间向量判断空间中的位置关系的常用方法
(1)线线平行
证明两条直线平行,只需证明两条直线的方向向量是共线向量.
(2)线线垂直
证明两条直线垂直,只需证明两条直线的方向向量垂直,即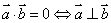 .
.
(3)线面平行
用向量证明线面平行的方法主要有:
①证明直线的方向向量与平面的法向量垂直;
②证明可在平面内找到一个向量与直线方向向量是共线向量;
③利用共面向量定理,即证明可在平面内找到两不共线向量来线性表示直线的方向向量.
(4)线面垂直
用向量证明线面垂直的方法主要有:
①证明直线方向向量与平面法向量平行;
②利用线面垂直的判定定理转化为线线垂直问题.
(5)面面平行
①证明两个平面的法向量平行(即是共线向量);
②转化为线面平行、线线平行问题.
(6)面面垂直
①证明两个平面的法向量互相垂直;
②转化为线面垂直、线线垂直问题.
6、运用空间向量求空间角
(1)求两异面直线所成角
利用公式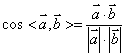 ,
,
但务必注意两异面直线所成角θ的范围是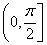 ,
,
故实质上应有: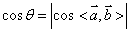 .
.
(2)求线面角
求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量,通过数量积求出直线与平面所成角;另一种方法是借助平面的法向量,先求出直线方向向量与平面法向量的夹角φ,即可求出直线与平面所成的角θ,其关系是sinθ=| cosφ|.
(3)求二面角
用向量法求二面角也有两种方法:一种方法是利用平面角的定义,在两个面内先求出与棱垂直的两条直线对应的方向向量,然后求出这两个方向向量的夹角,由此可求出二面角的大小;另一种方法是转化为求二面角的两个面的法向量的夹角,它与二面角的大小相等或互补.
7、运用空间向量求空间距离
空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离.
(1)点与点的距离
点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模.
(2)点与面的距离
点面距离的求解步骤是:
①求出该平面的一个法向量;
②求出从该点出发的平面的任一条斜线段对应的向量;
③求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得要求的点面距离.
备考建议:
1、空间向量的引入,把平面向量及其运算推广到空间,运用空间向量解决有关直线、平面位置关系的问题,应体会向量方法在研究几何图形中的作用,进一步发展空间想像能力和几何直观能力.
2、灵活选择运用向量方法与综合方法,从不同角度解决立体几何问题.
3、在解决立体几何中有关平行、垂直、夹角、距离等问题时,直线的方向向量与平面的法向量有着举足轻重的地位和作用,它的特点是用代数方法解决立体几何问题,无需进行繁、难的几何作图和推理论证,起着从抽象到具体、化难为易的作用.因此,应熟练掌握平面法向量的求法和用法.
4、加强运算能力的培养,提高运算的速度和准确性.
第一讲 空间向量及运算
一、空间向量的有关概念
1、空间向量的定义
在空间中,既有大小又有方向的量叫做空间向量.注意空间向量和数量的区别.数量是只有大小而没有方向的量.
2、空间向量的表示方法
空间向量与平面向量一样,也可以用有向线段来表示,用有向线段的长度表示向量的大小,用有向线段的方向表示向量的方向.若向量 对应的有向线段的起点是A,终点是B,则向量
对应的有向线段的起点是A,终点是B,则向量 可以记为
可以记为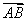 ,其模长为
,其模长为 或
或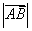 .
.
3、零向量
长度为零的向量称为零向量,记为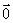 .零向量的方向不确定,是任意的.由于零向量的这一特殊性,在解题中一定要看清题目中所指向量是“零向量”还是“非零向量”.
.零向量的方向不确定,是任意的.由于零向量的这一特殊性,在解题中一定要看清题目中所指向量是“零向量”还是“非零向量”.
4、单位向量
模长为1的向量叫做单位向量.单位向量是一种常用的、重要的空间向量,在以后的学习中还要经常用到.
5、相等向量
长度相等且方向相同的空间向量叫做相等向量.若向量 与向量
与向量 相等,记为
相等,记为 =
= .零向量与零向量相等,任意两个相等的非零向量都可以用空间中的同一条有向线段来表示,并且与有向线段的起点无关.
.零向量与零向量相等,任意两个相等的非零向量都可以用空间中的同一条有向线段来表示,并且与有向线段的起点无关.
6、相反向量
长度相等但方向相反的两个向量叫做相反向量.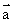 的相反向量记为-
的相反向量记为-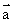
二、共面向量
1、定义
平行于同一平面的向量叫做共面向量.
2、共面向量定理
若两个向量 、
、 不共线,则向量
不共线,则向量 与向量
与向量 、
、 共面的充要条件是存在实数对x、y,使得
共面的充要条件是存在实数对x、y,使得 =
=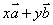 。
。
3、空间平面的表达式
空间一点P位于平面MAB内的充要条件是存在有序实数对x、y使 或对空间任一定点O,有
或对空间任一定点O,有
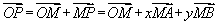 或
或 (其中
(其中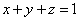 )这几个式子是M,A,B,P四点共面的充要条件.
)这几个式子是M,A,B,P四点共面的充要条件.
三、空间向量基本定理
1、定理
如果三个向量 、
、 、
、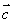 不共面,那么对空间任一向量
不共面,那么对空间任一向量 ,存在唯一的有序实数组x、y、z,使
,存在唯一的有序实数组x、y、z,使 =
=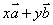
2、注意以下问题
(1)空间任意三个不共面的向量都可以作为空间向量的一个基底.
(2)由于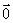 可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是
可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是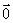 。
。
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,两者是相关联的不同概念.
由空间向量的基本定理知,若三个向量 、
、 、
、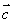 不共面。那么所有空间向量所组成的集合就是
不共面。那么所有空间向量所组成的集合就是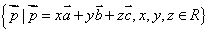 ,这个集合可看做是由向量
,这个集合可看做是由向量 、
、 、
、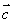 生成的,所以我们把
生成的,所以我们把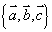 称为空间的一个基底。
称为空间的一个基底。 、
、 、
、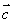 叫做基向量,空间任意三个不共面的向量都可构成空间的一个基底.
叫做基向量,空间任意三个不共面的向量都可构成空间的一个基底.
3、向量的坐标表示
(1)单位正交基底
如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用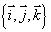 表示.
表示.
(2)空间直角坐标系
在空间选定一点O和一个单位正交基底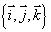 以点O为原点,分别以
以点O为原点,分别以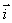 、
、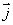 、
、 的方向为正方向建立三条数轴:x轴、y轴、z轴,它们都叫坐标轴.则建立了一个空间直角坐标系O-xyz,点O叫原点,向量
的方向为正方向建立三条数轴:x轴、y轴、z轴,它们都叫坐标轴.则建立了一个空间直角坐标系O-xyz,点O叫原点,向量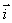 、
、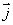 、
、 都叫坐标向量.
都叫坐标向量.
(3)空间向量的坐标
给定一个空间直角坐标系和向量 ,且设
,且设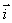 、
、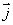 、
、 为坐标向量,存在唯一有序数组(x,y,z)使
为坐标向量,存在唯一有序数组(x,y,z)使 ,有序数组(x,y,z)叫做
,有序数组(x,y,z)叫做 在空间直角坐标系O-xyz中的坐标,记为
在空间直角坐标系O-xyz中的坐标,记为 =
=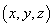 。
。
对坐标系中任一点A,对应一个向量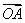 ,则
,则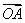 =
= 。在单位正交基底
。在单位正交基底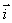 、
、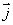 、
、 中与向量
中与向量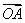 对应的有序实数组(x,y,z),叫做点A在此空间直角坐标系中的坐标,记为A(x,y,z).
对应的有序实数组(x,y,z),叫做点A在此空间直角坐标系中的坐标,记为A(x,y,z).
四、空间向量的运算
1、空间向量的加法
三角形法则(注意首尾相连)、平行四边形法则,
加法的运算律:交换律 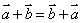
结合律 
2、空间向量的减法及几何作法
几何作法:在平面内任取一点O,作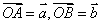 ,则
,则 ,即从
,即从 的终点指向
的终点指向 的终点的向量,这就是向量减法的几何意义.
的终点的向量,这就是向量减法的几何意义.
3、空间向量的数乘运算
(1)定义
实数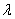 与
与 的积是一个向量,记为
的积是一个向量,记为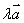 ,它的模与方向规定如下:
,它的模与方向规定如下:
① 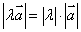
② 当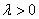 时,
时,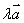 与
与 同向;当
同向;当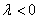 时,
时,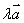 与
与 异向;当
异向;当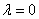 时.
时.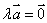
注意:
① 关于实数与空间向量的积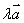 的理解:我们可以把
的理解:我们可以把 的模扩大(当
的模扩大(当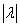 >1时),也可以缩小(
>1时),也可以缩小(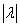 < 1 时),同时,我们可以不改变向量
< 1 时),同时,我们可以不改变向量 的方向(当
的方向(当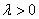 时),也可以改变向量
时),也可以改变向量 的方向(当
的方向(当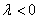 时)。 .
时)。 .
② 注意实数与向量的积的特殊情况,当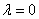 时,
时,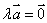 ;当
;当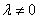 ,若
,若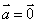 时,有
时,有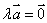 。
。
③ 注意实数与向量可以求积,但是不能进行加减运算.比如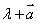 ,
,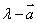 无法运算。
无法运算。
(2)实数与空间向量的积满足的运算律
设λ、μ是实数,则有
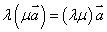 (结合律)
(结合律)
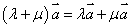 (第一分配律)
(第一分配律)
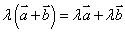 (第二分配律)
(第二分配律)
实数与向量的积也叫数乘向量.
4、共线向量
(1)共线向量定义
若表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量,也叫做平行向量。若 与
与 是共线向量,则记为
是共线向量,则记为 //
// 。
。
注意:零向量和空间任一向量是共线向量.
(2)共线向量定理
对空间任意两个向量 、
、 (
( ≠
≠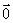 ),
), //
// 的充要条件是存在实数λ使
的充要条件是存在实数λ使 =λ
=λ
(3)空间直线的向量表示式
如果直线 l 是经过已知点 A 且平行于已知非零向量 的直线,那么对任一点 O,点P在直线 l 上的充要条件是存在实数t,满足等式
的直线,那么对任一点 O,点P在直线 l 上的充要条件是存在实数t,满足等式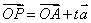 ,其中向量
,其中向量 叫做直线 l 的方向向量.
叫做直线 l 的方向向量.
注意:
①若在 l 上取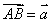 ,则有
,则有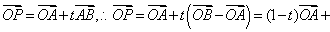

②上式可解决三点P、A、B 共线问题的表示或判定.
③当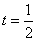 时,
时, ,点P为AB的中点,这是中点公式的向量表达式.
,点P为AB的中点,这是中点公式的向量表达式.
④ 若P分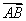 所成比为
所成比为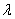 ,则
,则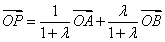
5、空间直角坐标系
在空间直角坐标系中,三条坐标轴两两互相垂直,轴的方向通常这样选择:从z轴的正方向看,x轴正半轴沿逆时针方向转 900能与 y 轴的正半轴重合。让右手拇指指向 x 轴正方向.食指指向 y 轴的正方向,如果中指指向 z 轴的正方向,那么称这个坐标系为右手直角坐标系。一般情况下,建立的坐标系都是右手直角坐标系.
在平面上画空间直角坐标系 O-xyz 时,一般使∠xOy=135°,∠yOz=90°。
空间两点间的距离公式是平面上两点间距离公式的推广,是空间向量模长公式的推广,如果知道儿何体上任意两点的坐标.我们就可直接套用.
设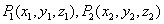 ,则
,则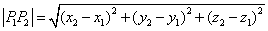
特别地,P1(x,y,z)到原点的距离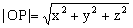
6、空间向量的数量积运算
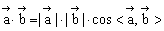
其中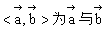 的夹角,范围是[0,π],注意数量积的性质和运算律。
的夹角,范围是[0,π],注意数量积的性质和运算律。
1. 性质
若 是非零向量,
是非零向量,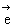 是与
是与 方向相同的单位向量,θ是
方向相同的单位向量,θ是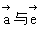 的夹角,则
的夹角,则
(1)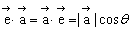
(2)
(3)若 同向,则
同向,则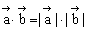 ;
;
若 反向,则
反向,则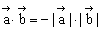 ;
;
特别地: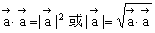
(4)若θ为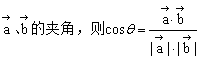
(5)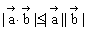
2. 运算律
(1)结合律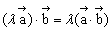
(2)交换律
(3)分配律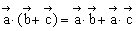
不满足消去律和结合律即:

【典型例题】
例1. 已知P是平面四边形ABCD所在平面外一点,连结PA、PB、PC、PD,点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心。求证:E、F、G、H四点共面。
证明:分别延长PE、PF、PG、PH交对边于M、N、Q、R
∵E、F、G、H分别是所在三角形的重心
∴M、N、Q、R为所在边的中点,顺次连结MNQR所得四边形为平行四边形,且有
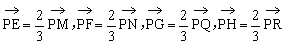
∵MNQR为平行四边形,则
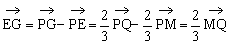
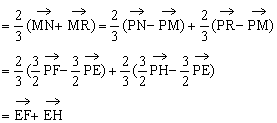
∴由共面向量定理得E、F、G、H四点共面。
例2. 如图所示,在平行六面体 中,
中,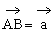 ,
,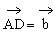 ,
,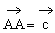 ,P是CA'的中点,M是CD'的中点,N是C'D'的中点,点Q是CA'上的点,且CQ:QA'=4:1,用基底
,P是CA'的中点,M是CD'的中点,N是C'D'的中点,点Q是CA'上的点,且CQ:QA'=4:1,用基底 表示以下向量:
表示以下向量:
(1)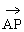 ;(2)
;(2)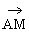 ;(3)
;(3)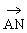 ;(4)
;(4)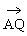 。
。
解:连结AC、AD'

(1)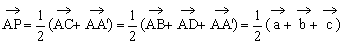 ;
;
(2) ;
;
(3)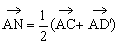
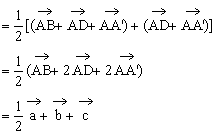
(4)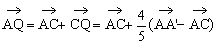
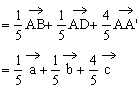
点评:本例是空间向量基本定理的推论的应用.此推论意在用分解定理确定点的位置,它对于以后用向量方法解几何问题很有用,选定空间不共面的三个向量作基向量.并用它们表示出指定的向量,是用向量解决几何问题的一项基本功.
例3. 已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC。M、N分别是OA、BC的中点,G是MN的中点。求证:OG⊥BC。
证明:连结ON,设∠AOB=∠BOC=∠AOC=θ
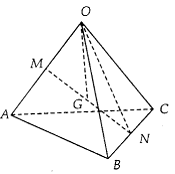
又设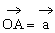 ,
,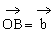 ,
,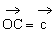 ,则
,则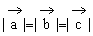 。
。
又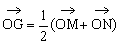
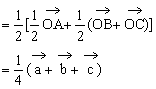
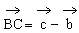
∴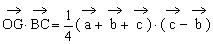
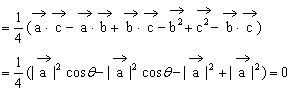
∴OG⊥BC
例4. 已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5)。
(1)求以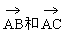 为邻边的平行四边形面积;
为邻边的平行四边形面积;
(2)若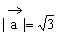 ,且
,且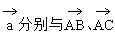 垂直,求向量
垂直,求向量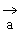 的坐标。
的坐标。
解:(1)由题中条件可知

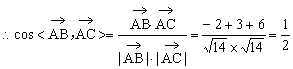
∴
∴以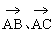 为邻边的平行四边形面积:
为邻边的平行四边形面积:
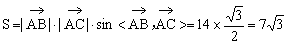
(2)设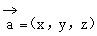 由题意得
由题意得
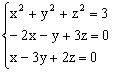
解得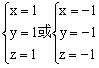
∴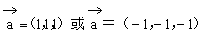
第二讲 直线的方向向量、平面的法向量及其应用
一、直线的方向向量及其应用
1、直线的方向向量
直线的方向向量就是指和这条直线所对应向量平行(或共线)的向量,显然一条直线的方向向量可以有无数个.
2、直线方向向量的应用
利用直线的方向向量,可以确定空间中的直线和平面.
(1)若有直线l, 点A是直线l上一点,向量 是l的方向向量,在直线l上取
是l的方向向量,在直线l上取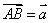 ,则对于直线l上任意一点P,一定存在实数t,使得
,则对于直线l上任意一点P,一定存在实数t,使得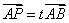 ,这样,点A和向量
,这样,点A和向量 不仅可以确定l的位置,还可具体表示出l上的任意点.
不仅可以确定l的位置,还可具体表示出l上的任意点.
(2)空间中平面α的位置可以由α上两条相交直线确定,若设这两条直线交于点O,它们的方向向量分别是 和
和 ,P为平面α上任意一点,由平面向量基本定理可知,存在有序实数对(x,y),使得
,P为平面α上任意一点,由平面向量基本定理可知,存在有序实数对(x,y),使得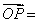
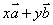 ,这样,点O与方向向量
,这样,点O与方向向量 、
、 不仅可以确定平面α的位置,还可以具体表示出α上的任意点.
不仅可以确定平面α的位置,还可以具体表示出α上的任意点.
二、平面的法向量
1、所谓平面的法向量,就是指所在的直线与平面垂直的向量,显然一个平面的法向量也有无数个,它们是共线向量.
2、在空间中,给定一个点A和一个向量 ,那么以向量
,那么以向量 为法向量且经过点A的平面是唯一确定的.
为法向量且经过点A的平面是唯一确定的.
三、直线方向向量与平面法向量在确定直线、平面位置关系中的应用
1、若两直线l1、l2的方向向量分别是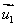 、
、 ,则有l1// l2
,则有l1// l2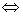
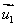 //
// ,l1⊥l2
,l1⊥l2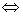
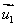 ⊥
⊥ .
.
2、若两平面α、β的法向量分别是 、
、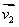 ,则有α//β
,则有α//β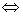
 //
//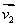 ,α⊥β
,α⊥β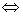
 ⊥
⊥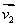 .
.
若直线l的方向向量是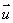 ,平面的法向量是
,平面的法向量是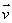 ,则有l//α
,则有l//α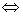
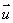 ⊥
⊥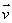 ,l⊥α
,l⊥α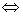
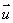 //
//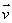
四、平面法向量的求法
若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:
1、设出平面的法向量为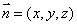 .
.
2、找出(求出)平面内的两个不共线的向量的坐标
3、根据法向量的定义建立关于x,y,z的方程组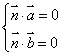
4、解方程组,取其中一个解,即得法向量
五、用向量方法证明空间中的平行关系和垂直关系
(一)用向量方法证明空间中的平行关系
空间中的平行关系主要是指:线线平行、线面平行、面面平行.
1、线线平行
设直线l1、l2的方向向量分别是 、
、 ,则要证明l1// l2,只需证明
,则要证明l1// l2,只需证明 //
// ,即
,即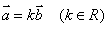
2、线面平行
(1)设直线l的方向向量是 ,平面
,平面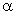 的法向量是
的法向量是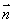 ,则要证明
,则要证明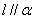 ,只需证明
,只需证明 ,即
,即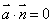 .
.
(2)根据线面平行的判定定理:“如果直线(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可.
(3)根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
3、面面平行
(1)由面面平行的判定定理,要证明面面平行,只要转化为相应的线面平行、线线平行即可.
(2)若能求出平面α、β的法向量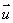 、
、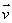 ,则要证明α//β,只需证明
,则要证明α//β,只需证明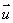 //
// 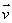
(二)用向量方法证明空间中的垂直关系
空间中的垂直关系主要是指:线线垂直、线面垂直、面面垂直.
1、线线垂直
设直线l1、l2的方向向量分别是 、
、 ,则要证明l1⊥ l2,只需证明
,则要证明l1⊥ l2,只需证明 ⊥
⊥ ,即
,即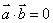
2、线面垂直
(1)设直线l的方向向量是 ,平面α的法向量是
,平面α的法向量是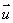 ,则要证l⊥α,只需证明
,则要证l⊥α,只需证明 //
// 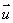
(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直.
3、面面垂直
(1)根据面面垂直的判定定理转化为证相应的线面垂直、线线垂直.
(2)证明两个平面的法向量互相垂直.
六、用向量方法求空间的角
(一)两条异面直线所成的角
1、定义:设a、b是两条异面直线,过空间任一点O作直线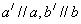 ,则
,则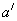 与
与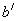 所夹的锐角或直角叫做a与b所成的角.
所夹的锐角或直角叫做a与b所成的角.
2、范围:两异面直线所成角θ的取值范围是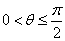
3、向量求法:设直线a、b的方向向量为 、
、 ,其夹角为
,其夹角为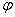 ,则有
,则有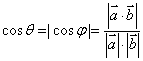
4、注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但两者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
(二)直线与平面所成的角
1、定义:直线和平面所成的角,是指直线与它在这个平面内的射影所成的角.
2、范围:直线和平面所成角θ的取值范围是
3、向量求法:设直线l的方向向量为 ,平面的法向量为
,平面的法向量为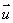 ,直线与平面所成的角为θ,
,直线与平面所成的角为θ, 与
与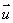 的夹角为
的夹角为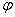 ,则有
,则有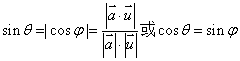
(三)二面角
1、二面角的取值范围: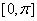
2、二面角的向量求法
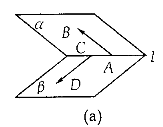
(1)若AB、CD分别是二面角 的两个面内与棱l垂直的异面直线,则二面角的大小就是向量
的两个面内与棱l垂直的异面直线,则二面角的大小就是向量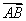 与
与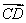 的夹角(如图(a)所示).
的夹角(如图(a)所示).
(2)设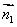 、
、 是二面角
是二面角 的两个角α、β的法向量,则向量
的两个角α、β的法向量,则向量 与
与 的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).
的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).
七、用向量的方法求空间的距离
(一)点面距离的求法
如图(a)所示,BO⊥平面α,垂足为O,则点B到平面α的距离就是线段BO的长度.若AB是平面α的任一条斜线段,则在Rt△BOA中,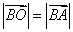 cos∠ABO=
cos∠ABO=
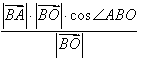 。如果令平面α的法向量为
。如果令平面α的法向量为 ,考虑到法向量的方向,可以得到B点到平面α的距离为
,考虑到法向量的方向,可以得到B点到平面α的距离为 。
。
因此要求一个点到平面的距离,可以分以下几步完成:
1、求出该平面的一个法向量.
2、找出从该点出发的平面的任一条斜线段对应的向量.
3、求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离.
由于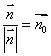 可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即
可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即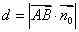 .
.
另外,等积法也是点到面距离的常用求法.
(二)线面距、面面距均可转化为点面距离用求点面距的方法进行求解。
(三)两异面直线距离的求法
如图(b)所示,设l1、l2是两条异面直线,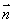 是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是
是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是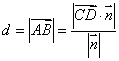 。
。
【典型例题】
例1. 设 分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
(1)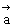 =(2,3,-1),
=(2,3,-1), =(-6,-9,3);
=(-6,-9,3);
(2)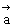 =(5,0,2),
=(5,0,2), =(0,4,0);
=(0,4,0);
(3)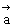 =(-2,1,4),
=(-2,1,4), =(6,3,3)
=(6,3,3)
解:(1)∵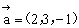 ,
, =(-6,-9,3)
=(-6,-9,3)
∴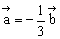 ,∴
,∴ ,∴l1//l2
,∴l1//l2
(2)∵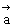 =(5,0,2),
=(5,0,2), =(0,4,0)
=(0,4,0)
∴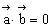 ,∴
,∴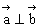 ,∴l1⊥l2
,∴l1⊥l2
(3)∵ (-2,1,4,),
(-2,1,4,), =(6,3,3)
=(6,3,3)
∴ 不共线,也不垂直
不共线,也不垂直
∴l1与l2的位置关系是相交或异面
例2. 设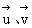 分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
(1)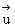 =(1,-1,2),
=(1,-1,2), =(3,2,
=(3,2,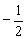 );
);
(2)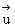 =(0,3,0),
=(0,3,0), =(0,-5,0);
=(0,-5,0);
(3)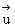 =(2,-3,4),
=(2,-3,4), =(4,-2,1)。
=(4,-2,1)。
解:(1)∵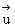 =(1,-1,2),
=(1,-1,2), =(3,2,
=(3,2,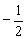 )
)
∴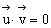
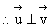 ∴α⊥β
∴α⊥β
(2)∵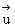 =(0,3,0),
=(0,3,0), =(0,-5,0)
=(0,-5,0)
∴
(3)∵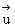 =(2,-3,4),
=(2,-3,4), =(4,-2,1)
=(4,-2,1)
∴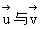 既不共线、也不垂直,∴α与β相交
既不共线、也不垂直,∴α与β相交
点评:应熟练掌握利用向量共线、垂直的条件。
例3. 已知点A(3,0,0),B(0,4,0),C(0,0,5),求平面ABC的一个单位法向量。
解:由于A(3,0,0),B(0,4,0),C(0,0,5),∴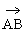 =(-3,4,0),
=(-3,4,0),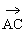 =(-3,0,5)
=(-3,0,5)
设平面ABC的法向量为 (x,y,z)
(x,y,z)
则有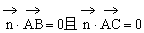
即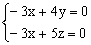 取z=1,得
取z=1,得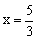 ,
,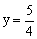
于是 =(
=(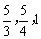 ),又
),又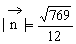
∴平面α的单位法向量是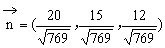
例4. 若直线l的方向向量是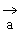 =(1,2,2),平面α的法向量是
=(1,2,2),平面α的法向量是 =(-1,3,0),试求直线l与平面α所成角的余弦值。
=(-1,3,0),试求直线l与平面α所成角的余弦值。
分析:如图所示,直线l与平面α所成的角就是直线l与它在平面内的射影所成的角,即∠ABO,而在Rt△ABO中,∠ABO=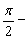 ∠BAO,又∠BAO可以看作是直线l与平面α的垂线所成的锐角,这样∠BAO就与直线l的方向向量a与平面α的法向量n的夹角建立了联系,故可借助向量的运算求出∠BAO,从而求出∠ABO,得到直线与平面所成的角。
∠BAO,又∠BAO可以看作是直线l与平面α的垂线所成的锐角,这样∠BAO就与直线l的方向向量a与平面α的法向量n的夹角建立了联系,故可借助向量的运算求出∠BAO,从而求出∠ABO,得到直线与平面所成的角。
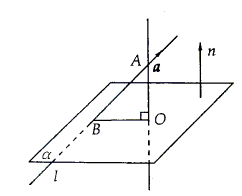
解:∵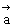 =(1,2,2,),
=(1,2,2,),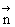 =(-1,3,0)
=(-1,3,0)
∴ ,
, ,
,
∴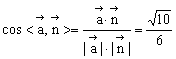
若设直线l与平面α所成的角是θ
则有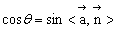
∵
∴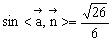
因此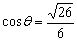 ,即直线l与平面α所成角的余弦值等于
,即直线l与平面α所成角的余弦值等于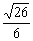 。
。
例5. 如图(a)所示,在正方体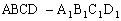 中,M、N分别是
中,M、N分别是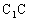 、
、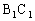 的中点。
的中点。
求证:(1)MN//平面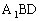 ;
;
(2)平面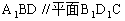 。
。
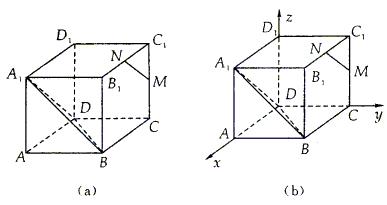
(1)证法一:如图(b)所示,以D为原点,DA、DC、 所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设正方体的棱长为1,则可求得M(0,1,
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设正方体的棱长为1,则可求得M(0,1,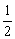 ),N(
),N(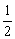 ,1,1,),D(0,0,0),
,1,1,),D(0,0,0),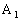 (1,0,1),B(1,1,0),于是
(1,0,1),B(1,1,0),于是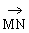 =(
=(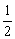 ,0,
,0,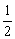 )。
)。
设平面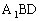 的法向量是
的法向量是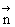 (x,y,z)
(x,y,z)
则 ,得
,得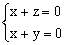
取x=1,得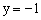 ,
,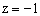 ,
,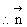 =(1,-1,-1)
=(1,-1,-1)
又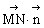 =(
=(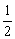 ,0,
,0,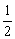 )·(1,-1,-1)=0,∴
)·(1,-1,-1)=0,∴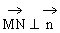
∴MN//平面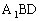
证法二:∵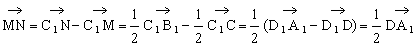
∴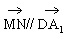 ,∴
,∴
证法三:∵
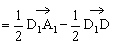
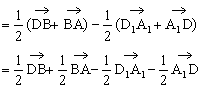
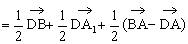

即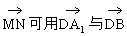 线性表示,故
线性表示,故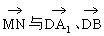 是共面向量
是共面向量
∴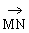 //平面A1BD,即MN//平面A1BD。
//平面A1BD,即MN//平面A1BD。
(2)证明:由(1)求得平面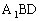 的法向量为
的法向量为 =(1,-1,-1)
=(1,-1,-1)
同理可求平面B1D1C的法向量 =(1,-1,-1)
=(1,-1,-1)
∴
∴平面A1BD//平面B1D1C
例6. 如图,在正方体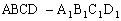 中,O为AC与BD的交点,G为CC1的中点。求证:A1O⊥平面GBD。
中,O为AC与BD的交点,G为CC1的中点。求证:A1O⊥平面GBD。
证明:设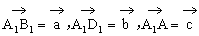 ,则
,则
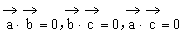
而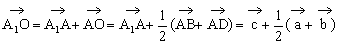
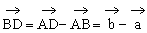
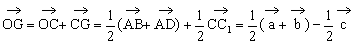
∴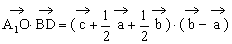
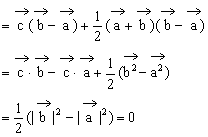
同理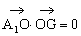
∴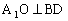 ,
,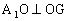
又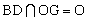 ,∴
,∴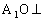 面GBD。
面GBD。
例7. (20##年天津)如图(a)所示,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点。
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成角的正切值。
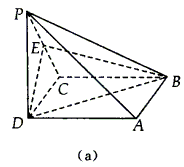
(1)证明:如图(b)所示建立空间直角坐标系,D为坐标原点
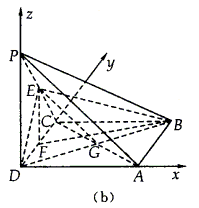
设DC=a,连结AC,AC交BD于G,连结EG
依题意得A(a,0,0),P(0,0,a),E(0,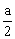 ,
,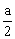 )
)
∵底面ABCD是正方形
∴G是此正方形的中心
故点G的坐标为(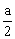 ,
,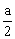 ,0)
,0)
∴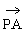 =(a,0,-a),
=(a,0,-a),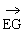 =(
=(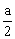 ,0,
,0,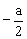 )
)
∴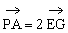 ,这表明PA//EG
,这表明PA//EG
而EG 平面EDB,且PA
平面EDB,且PA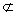 平面EDB
平面EDB
∴PA//平面EDB
(2)解:依题意得B(a,a,0),C(0,a,0)
如图(b)取DC的中点F(0,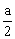 ,0),连结EF、BF
,0),连结EF、BF
∵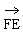 =(0,0,
=(0,0, 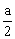 ),
),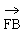 =(a,
=(a,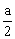 ,0),
,0),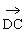 =(0,a,0)
=(0,a,0)
∴ ,
,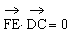
∴FE⊥FB,FE⊥DC。
∴tan∠EBF
∴EB与底面ABCD所成角的正切值为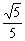
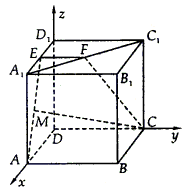
例8. 正方体 中,E、F分别是
中,E、F分别是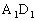 、
、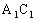 的中点,求:
的中点,求:
(1)异面直线AE与CF所成角的余弦值;
(2)二面角C—AE—F的余弦值的大小。
解:不妨设正方体棱长为2,分别取DA、DC、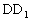 所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(2,0,0),C(0,2,0),E(1,0,2),F(1,1,2)
所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(2,0,0),C(0,2,0),E(1,0,2),F(1,1,2)
(1)由 =(-1,0,2),
=(-1,0,2),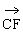 =(1,-1,2),得
=(1,-1,2),得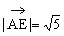 ,
,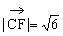
∴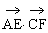 =-1+0+4=3
=-1+0+4=3
又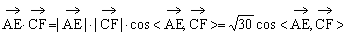
∴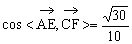 ,∴所求值为
,∴所求值为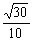
(2)∵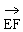 =(0,1,0)
=(0,1,0)
∴ =(-1,0,2)·(0,1,0)=0
=(-1,0,2)·(0,1,0)=0
∴AE⊥EF,过C作CM⊥AE于M
则二面角C—AE—F的大小等于
∵M在AE上,∴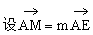
则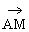 =(-m,0,2m),
=(-m,0,2m), =(-2,2,0)-(-m,0,2m)=(m-2,2,-2m)
=(-2,2,0)-(-m,0,2m)=(m-2,2,-2m)
∵MC⊥AE
∴ =(m-2,2,-2m)·(-1,0,2)=0
=(m-2,2,-2m)·(-1,0,2)=0
∴ ,∴
,∴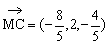 ,
,
∴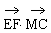 =(0,1,0)·(
=(0,1,0)·( ,2,
,2,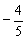 )=0+2+0=2
)=0+2+0=2
又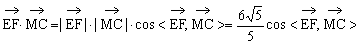
∴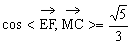
∴二面角C—AE—F的余弦值的大小为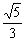
例9. 已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,H是EF与AC的交点,CG⊥面ABCD,且CG=2。求BD到面EFG的距离。
分析:因BD//平面EFG,故O到面EFG与BD到面EFG距离相等,证明OM垂直于面EFG即可。
解:如图所示,分别以CD、CB、CG所在直线为x、y、z轴建立空间直角坐标系。
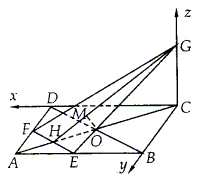
易证BD//面EFG,设 =O,EF⊥面CGH,O到面EFG的距离等于BD到面EFG的距离,过O作OM⊥HG于M,易证OM⊥面EFG,可知OM为所求距离。另易知H(3,3,0),G(0,0,2),O(2,2,0)。
=O,EF⊥面CGH,O到面EFG的距离等于BD到面EFG的距离,过O作OM⊥HG于M,易证OM⊥面EFG,可知OM为所求距离。另易知H(3,3,0),G(0,0,2),O(2,2,0)。
设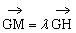 ,
, =(3,3,-2)
=(3,3,-2)
则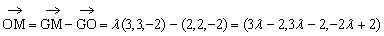
又 ,∴
,∴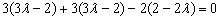
∴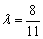 ,∴
,∴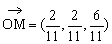
∴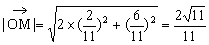
即BD到平面EFG的距离等于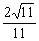
【励志故事】
习惯
父子俩住山上,每天都要赶牛车下山卖柴。老父较有经验,坐镇驾车,山路崎岖,弯道特多,儿子眼神较好,总是在要转弯时提醒道:“爹,转弯啦!”
有一次父亲因病没有下山,儿子一人驾车。到了弯道,牛怎么也不肯转弯,儿子用尽各种方法,下车又推又拉,用青草诱之,牛一动不动。
到底是怎么回事?儿子百思不得其解。最后只有一个办法了,他左右看看无人,贴近牛的耳朵大声叫道:“爹,转弯啦!”
牛应声而动。
牛用条件反射的方式活着,而人则以习惯生活。一个成功的人晓得如何培养好的习惯来代替坏的习惯,当好的习惯积累多了,自然会有一个好的人生。
