高等数学第二学期总结
大学一年级已接近尾声,大一高数的学习也已经完成,下学期的高数学习随着知识的深入而带领我们更进一步去了解高数学习的真谛和高数的重要性。从高数的学习中我获得了更为广阔的知识和视野,下学期的学习既是上学期的学习内容的拓展又是延伸,使我们对高数有更一步的了解和认识,让我们对这门课的研究更为深入。
大一下学期的高数学习分为六章,分别是向量代数与空间解析几何,多元函数微分学,重积分,无穷级数,微分方程和差分方程。在向量代数与空间解析几何中,我们首先学习了向量代数的基本知识,从而在后来的学习中使用向量的基本知识来解决空间几何问题。本章中我们学习的解析几何是17世纪前半叶产生的一门全新的几何学。法国数学家笛卡尔是解析几何的主要创立人。空间解析几何就是用代数的方法研究空间图形的性质。向量是一种重要的数学工具,是近代数学的基本概念之一,在中学阶段,我们已经学习过如何利用向量来解决一些简单的几何问题,这一章在中学学习的基础上,以向量为工具研究空间曲面和空间曲线,介绍空间几何的基本内容,是学习多元函数微分学和积分学的基础。
这一章中,首先介绍了向量代数的基础知识,然后通过建立空间直角坐标系,研究空间中平面与直线方程、常见曲线与曲面等内容。主要的学习方向就是解决空间几何体的相关问题,例如求解空间几何体的面积、体积、距离等相关量。特别当我们在求解曲面时,应该注意使用不同的坐标系,来求解不同的曲面,比如有柱面坐标、直角坐标等。
在多元函数微分学的学习中,上一章就已经学习了一些有关一元函数的微积分,但在许多实际问题中,往往涉及多个因素之间的关系,反映到数学上就表现为一个变量依赖于多个变量的情形,从而产生了多元函数的概念。因此,我们就有必要研究多元函数的微积分问题。
本章主要采用类比的方法来帮助我们理解多元函数的定义,通过将多元函数与一元函数微分基本理论的类比,归纳总结出多元函数微分学的基本理论,主要讨论二元函数的极限与连续的概念、偏导数与全微分及其应用。
要学习多元函数微分学,就必须要先了解多元函数的基本概念和极限,本章在第一节中就介绍了有关这方面的内容。学习多元函数的重点是学习二元函数和三元函数,只要掌握了二元和三元函数的微分,则多元函数就基本掌握了。在第二节中,我们学习了偏导数。在研究一元函数时,我们就已经看到了函数关于自变量的变化率的重要性,对于二元函数也同样有函数变化率的问题。所以,我们就有必要学习一下这种变化率,即偏导数。在学习了偏导数这个工具之后,我们就要开始接触全微分,全微分是我们学习微分中的一个重要组成部分。我们学习的微分其实是建立在极限的基础上,所以,接着,我们又开始学习多元复合函数的求导法则以及隐函数的微分法等等与微分和极限有关的内容。
在接下来的一章中,我们开始学习重积分,一元函数的定积分是某种形式的极限,它在实际问题中有着广泛的应用。但由于其积分范围是数轴上的区间,因而只能用来计算与一元函数及其相应区间有关的量。在高等数学中,重积分是多元函数积分学的内容,在一元函数积分学中我们知道定积分是某种确定形式的和的极限。这种和的概念推广到定义在区域、曲线及曲面上多元函数的情形,便得到重积分、曲线积分及曲面积分的概念。高等数学讨论的重积分主要包括二重积分和三重积分两部分,引起二重积分概念的过程是测量曲顶柱体体积的过程的反映,三重积分概念是作为二重积分概念的推广而引出的,但事实上三重积分也是某些具体现实过程的反映。在本章中将介绍重积分的概念、计算法以及它们的一些应用。重积分在各种知识领域中的应用非常广阔,我们将在理论力学,材料力学,水力学及其她一些工程学科中碰到它们。
多元函数的积分要比一元函数的定积分复杂得多,当积分范围是平面或空间区域时,这样的积分就是重积分;当积分范围是曲线时,这样的积分就是曲线积分;当积分范围是曲面时,这样的积分就是曲面积分。定义这些积分的思想方法与定积分类似,都可以概括为分割、近似、求和、取极限四个步骤,本章讨论二重积分与三重积分的概念、性质、计算方法和它们的一些应用。
在无穷级数这一章中,课程介绍了无穷级数这个新的概念,无穷级数理论在高等数学中具有非常重要的地位,是研究微积分理论及其应用的强有力工
具。研究无穷级数,是研究数列的另一种形式,尤其在研究极限的存在性及计算极限方面显示出很大的优越性。它在表示函数、研究函数的性质、计算函数值以及求解微分方程等方面都有重要的应用,在经济、管理、电学以及振动理论等诸多领域离也有广泛的应用。
无穷级数是微积分学的重要组成部分之一,是表示函数、研究函数性质和进行数值计算的有力工具。无穷级数本质上是一种特殊数列的极限。利用极限,常数项级数是把有限个数相加推广到无穷多个数相加。幂级数是把多项式的次数推广到无穷多次的结果。主要掌握常数项级数收敛性判别法和会讨论幂级数收敛性。
本章首先介绍无穷级数的概念和基本性质,然后重点讨论常数项级数的概念、性质及其敛散性的判别法,在此基础上介绍函数项级数的相关类容,以及将函数展开成幂级数的条件和方法。
正项级数的收敛判别 :各项都是由正数组成的级数称为正项级数,正项级数收敛的充要条件是:部分和数列{sn}有界,即存在某正整数M,对一切正整
数 n有sn<M。从基本定理出发,我们可以由此建立一系列基本的判别法
1 比较判别法
设∑un和∑vn是两个正项级数,如果存在某正数N,对一切n>N都有un≦vn,则
(1)级数∑vn收敛,则级数∑un也收敛;
(2)若级数∑un发散,则级数∑vn也发散
2 柯西判别法(根式判别法)
设∑un为正项级数,且存在某正整数N0及正常数l,(1)若对一切n>
N0,成立不等式
式则级数l<1,则级数∑un收敛。(2)若对一切n>N0,成立不等∑un发散。
第十一章学习了微分方程,微分方程是数学建模最重要、最有效的工具之
一。本章重点阐述了微分方程的基本概念,讨论一些常见的一阶、二阶微分方程,并举例介绍微分方程在经济、管理等方面的简单应用。通过本章的学习,理解了微分方程的基本概念,掌握常见的一阶、二阶微分方程的基本解法,通过建立微分方程模型,解决一些简单的经济问题,培养对数学建模思想的理解。凡表示自变量,未知函数以及未知函数的导数或微分之间关系的方程称为微分方程。若方程中的未知函数为一元函数,就称为常微分方程;若方程中的未知函数为多元函数,这时导数为未知的偏导数,就称为偏微分方程。只含有未知函数的一阶导数,我们称这样的方程为一阶微分方程,而微分方程中含有未知函数的二阶导数,我们称这样的方程为二阶微分方程。一般的,若方程中未知函数的最高阶导数为n阶,则称其为n阶微分方程,并称方程中未知函数导数的最高阶数n为方程的阶。每一个微分方程转化为恰当方程之后,可以运用恰当方程的公式进行求解,因此转化成恰当方程是求解微分方程的重要步骤,转化成恰当方程需要求解出积分因子,因此积分因子的求解变得非常重要。课本中介绍了仅关于x或仅关于y的积分因子。
第十二章我们学习了差分方程,对于连续变量y(t),可以用刻画其变化率。但是在许多应用问题中,函数是否可导,甚至是否连续都不清楚,或函数根本就不可导,而只知道函数在某些时刻的函数值,这时自变量与因变量都是离散变化的。因此我们利用函数的差商△y/△t代替导数来刻画函数y(t)的变化率。我们对函数在单位时间内的增量引入了一个新的概念就是差分。本章中比较重要的是二阶常系数线性方程,这里学到了二阶常系数齐次线性差分方程的通解以及二阶常系数非齐次线性方程特解的解法。
在学习高数的时候,我们应该注重学习方法的选择,只有掌握好了学习方法,才能将这门课学好。我们在学习的时候,要先预习,然后应该好好的完成课后作业,最好要时刻的复习总结。学习高数这门课的时候,我们首先应该了解高数这门课的性质,对数学来说,结构无处不在,结构是由许多节点和联线
绘成的稳定系统。数学中最基本的就是概念结构,它们之间的联系组成了知识网络的结构,剖析高等数学的知识结构,有助于加深对高等数学的理解
高数以极限思想为灵魂,以微积分为核心,包括级数在内,它们都是从量的方面研究事物运动变化的数学方法,本质上是几种不同性质的极限问题。因此,我们在学习这些内容的时候应该掌握它们之间的联系,这样我们在学习的时候就可以做到事半功倍的效果。
我们学习高数要坚持下去,这样我们在取得良好成绩的同时就能体会到数学的独特魅力。学习好高数,对我们的生活学习都很有帮助,在数学的海洋里遨游,我们便能体会到宇宙的智慧。
第二篇:大一高等数学论文
20113564 胡骐薪 工商1112
微分方程的基本应用
微分方程是数学的重要分支, 用微分方程来刻画许多自然科学、经济科学甚至社会科学领域中的一些规律,这是微分方程应用的重要领域,也是其发展的动力.在这里我重点介绍了几个利用微分方程常来解决的问题的例子,从中我们可以了解到微分方程用的广泛性以及解决具体问题时常采用的一般步骤.
微分方程是与微积分一起形成发展起来的重要数学分支,已有悠久的历史,早在17~18世纪,牛顿、莱布尼兹、贝努里和拉格朗日等人在研究力学和几何学中就提出了微分方程【1,2】.随着科学的发展,它在力学、电学、天文学和其他数学物理领域内的应用不断获得成功,有力地推动了这些学科的发展,已成为研究自然科学和社会科学的一个强有力工具.如今,微分方程仍继续保持着进一步发展的活力,其主要原因是它的根源深扎在各种实际问题之中,许多实际问题可以通过建立微分方程模型得以解决.
常微分方程的形成与发展是和力学、天文学、物理学,以及其他科学技术的发展密切相关的. 数学的其他分支的新发展,如复变函数、李群、组合拓扑学等,都对常微分方程的发展产生了深刻的影响,当前计算机的发展更是为常微分方程的应用及理论研究提供了非常有力的工具.
微分方程可以精确地表述事物变化所遵循的基本规律. 随着微分方程的理论的逐步完善,只要列出相应的微分方程并找到解方程的方法, 微分方程也就成了最有生命力的数学分支. 事实上,大部分的常微分方程求不出十分精确的解,而只能得到近似解. 当然,这个近似解的精确程度是比较高的.
现在,常微分方程在很多学科领域内有着重要的应用,自动控制、各种电子学装置的设计、弹道的计算、飞机和导弹飞行的稳定性的研究、化学反应过程稳定性的研究等. 这些问题都可以化为求常微分方程的解,或者化为研究解的性质的问题. 应该说,应用常微分方程理论已经取得了很大的成就. 解常微分方程大致有分离变量法、变量替换法、常数变易法以及积分因子法等等,其中,积分因子法尤为重要,本论文主要讨论积分因子存在条件及其解法,通过积分因子使常微分方程化为全微分方程形式来求解.
微分方程在科学技术和实际生活中都有着广泛的应用。应用微分方程解决实际问题,其实就是建立微分方程数学模型,通过建立微分方程、确定定解条件、求解及对解的分析可以揭示许多自然界和科学技术中的规律.应用微分方程解决具体问题的主要步骤:
(1)分析问题,将实际问题抽象,设出未知函数,建立微分方程,并给出合理的定解条件;
(2)求解微分方程的通解及满足定解条件的特解,或由方程讨论解的性质;
(3)由所求得的解或解的性质,回到实际问题,解释该实际问题,得出客观规律.
微分方程的应用举例
几何问题
1.等角轨线
我们来求这样的曲线或曲线族,使得它与某已知曲线族的每一条曲线相交成给定的角度.这样的曲线轨线已知曲线的等角轨线.当所给定的角为直角时,等角轨线就轨线正交轨线.等角轨线在很多学科(如天文,气象等)中都有应用.下面就来介绍等角轨线的方法.
首先把问题进一步提明确一些.
设在(x,y)平面上,给定一个单参数曲线族(C):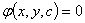 求这样的曲线
求这样的曲线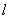 ,使得
,使得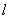 与(C)中每一条曲线的交角都是定角
与(C)中每一条曲线的交角都是定角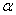 .
.
设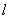 的方程为
的方程为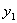 =
=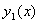 .为了求
.为了求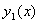 ,我们先来求出
,我们先来求出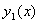 所对应满足的微分方程,也就是要求先求得
所对应满足的微分方程,也就是要求先求得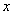 ,
, 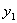 ,
,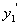 的关系式.条件告诉我们
的关系式.条件告诉我们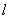 与(C)的曲线相交成定角
与(C)的曲线相交成定角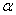 ,于是,可以想象,
,于是,可以想象,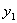 和
和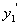 必然应当与(C)中的曲线
必然应当与(C)中的曲线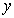 =
=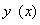 及其切线的斜率
及其切线的斜率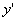 有一个关系.事实上,当
有一个关系.事实上,当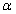 ≠
≠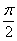 时,有
时,有
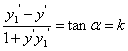
或
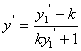
当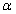 =
=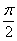 时,有
时,有
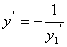
又因为在交点处,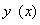 =
=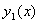 ,于是,如果我们能求得
,于是,如果我们能求得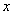 ,
, 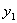 ,
,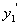 的关系
的关系
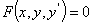
采用分析法.
设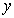 =
=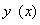 为(C)中任一条曲线,于是存在相应的C,使得
为(C)中任一条曲线,于是存在相应的C,使得
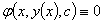
因为要求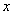 ,y,
,y, 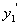 的关系,将上式对x求导,得
的关系,将上式对x求导,得
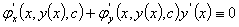
这样,将上两式联立,即由
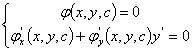
消去C,就得到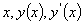 所应当满足的关系
所应当满足的关系
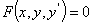
这个关系称为曲线族(C)的微分方程.
于是,等角轨线(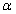 ≠
≠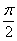 )的微分方程就是
)的微分方程就是
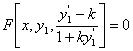
而正交轨线的微分方程为
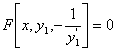
为了避免符号的繁琐,以上两个方程可以不用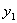 ,而仍用y,只要我们明确它是所求的等角轨线的方程就行了.
,而仍用y,只要我们明确它是所求的等角轨线的方程就行了.
为了求得等角轨线或正交轨线,我们只需求上述两个方程即可.
例1 求直线束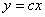 的等角轨线和正交轨线.
的等角轨线和正交轨线.
解 首先求直线束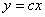 的微分方程.
的微分方程.
将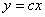 对
对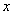 求导,得
求导,得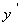 =C,由
=C,由
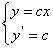
消去C,就得到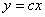 的微分方程
的微分方程
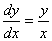
当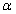 ≠
≠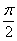 时,由(2.16)知道,等角轨线的微分方程为
时,由(2.16)知道,等角轨线的微分方程为
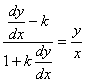
或
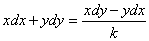
及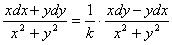
即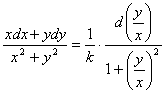
积分后得到
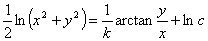
或
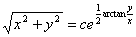
如果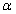 =
=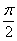 ,由(2.17)可知,正交轨线的微分方程为
,由(2.17)可知,正交轨线的微分方程为
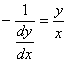
即 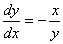
或 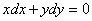
故正交轨线为同心圆族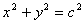 .
.
例2 抛物线的光学问题
在中学平面解析几何中已经指出,汽车前灯和探照灯的反射镜面都取为旋转抛物面,就是将抛物线绕对称轴旋转一周所形成的曲面.将光源安置在抛物线的焦点处,光线经镜面反射,就成为平行光线了.这个问题在平面解析几何中已经作了证明,现在来说明具有前述性质的曲线只有抛物线,
由于对称性,只有考虑在过旋转轴的一个平面上的轮廓线 ,如图,
,如图,
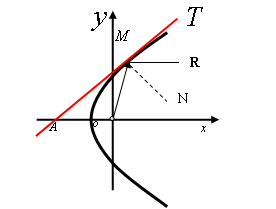
以旋转轴为Ox轴,光源放在原点O(0,0).设 的方程为y=y(x,y).由O点发出的光线经镜面反射后平行于Ox轴.设M(x,y)为
的方程为y=y(x,y).由O点发出的光线经镜面反射后平行于Ox轴.设M(x,y)为 上任一点,光线OM经反射后为MR.MT为
上任一点,光线OM经反射后为MR.MT为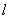 在M点的切线,MN为
在M点的切线,MN为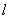 在M点的法线,根据光线的反射定律,有
在M点的法线,根据光线的反射定律,有
∠OMN=∠NMR
从而
tan∠OMN=tan∠NMR
因为MT的斜率为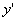 ,MN的斜率为-
,MN的斜率为-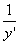 ,所以由正切公式,有
,所以由正切公式,有
tan∠OMN=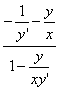 , tan∠NMR=
, tan∠NMR=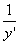
从而
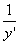 =-
=-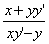
即得到微分方程
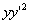 +2x
+2x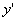 -y=0
-y=0
由这方程中解出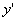 ,得到齐次方程
,得到齐次方程
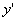 =-
=-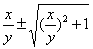
令 =u,即y=xu,有
=u,即y=xu,有
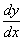 =u+
=u+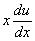
代入上式得到
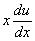 =
=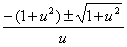
分离变量后得
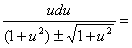
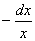
令1+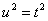 上式变为
上式变为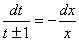 .积分后得
.积分后得
ln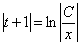
或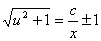 .两端平方得
.两端平方得
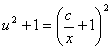
化简后得
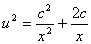
以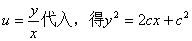 .这是一族以原点为焦点的抛物线.
.这是一族以原点为焦点的抛物线.
2.动力学问题
动力学是微分方程最早期的源泉之一.我们都知道动力学的基本定律是牛顿第二定律
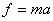
这也是用微分方程来解决动力学的基本关系式.它的右端明显地含有加速度a,a是位移对时间的二阶导数.列出微分方程的关键就在于找到外力f和位移对时间的导数-速度的关系.只要找到这个关系,就可以由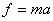 列出微分方程了.
列出微分方程了.
在求解动力学问题时,要特别注意力学问题中的定解条件,如初值条件等.
例:物体由高空下落,除受重力作用外,还受到空气阻力的作用,在速度不太大的情况下,空气阻力可看做与速度的平方成正比试证明在这种情况下,落体存在极限速度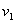 .
.
 解 设物体质量为m,空气阻力系数为k,又设在时刻t物体下落的速度为v,于是在时刻t物体所受的合外力为
解 设物体质量为m,空气阻力系数为k,又设在时刻t物体下落的速度为v,于是在时刻t物体所受的合外力为
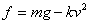 (重力-空气阻力)
(重力-空气阻力)
从而,根据牛顿第二定律可得出微分方程
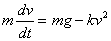
因为是自由落体,所以有
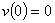
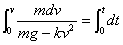
积分得
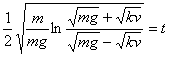
或
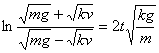
解出v,得
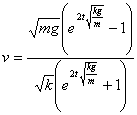
当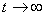 时,有
时,有
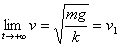
据测定,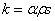 ,其中
,其中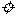 为与物体形状有关的常数,为介质密度,s为物体在地面上的投影面积.
为与物体形状有关的常数,为介质密度,s为物体在地面上的投影面积.
人们正是根据公式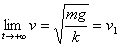 ,来为跳伞者设计保证安全的降落伞的直径大小的.在落地速度
,来为跳伞者设计保证安全的降落伞的直径大小的.在落地速度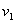 ,m,
,m, 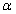 ,与 一定时,可定出s来.
,与 一定时,可定出s来.
3.流体混合问题
中学代数中有这样一类问题:某容器中装有浓度为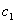 的含某种物质A的液体V升,从其中取出
的含某种物质A的液体V升,从其中取出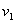 升后,加入浓度为
升后,加入浓度为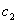 的液体
的液体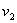 升,要求混合后的液体的浓度以及物质A的含量.这类问题用初等代数就可以解决了.
升,要求混合后的液体的浓度以及物质A的含量.这类问题用初等代数就可以解决了.
 但是,在实际中还经常碰到如下的问题:如图,
但是,在实际中还经常碰到如下的问题:如图,
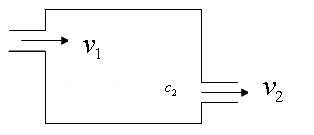
容器内装有含物质A的流体.设时刻t=0时,流体的体积为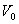 ,物质A的质量为
,物质A的质量为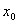 .今以速度
.今以速度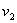 (单位时间的流量)放出流体,而同时又以速度
(单位时间的流量)放出流体,而同时又以速度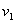 注入浓度为
注入浓度为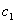 的流体,试求时刻t时容器中物质A的质量及流体的浓度. 这类问题称为流体混合问题.它是不能用初等数学解决的,必须用微分方程来计算.
的流体,试求时刻t时容器中物质A的质量及流体的浓度. 这类问题称为流体混合问题.它是不能用初等数学解决的,必须用微分方程来计算.
首先,我们用微元发来列方程.设在时刻t,容器内物质A的质量为x=x(t),浓度为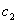 ,经过时间dt后,容器内物质A的质量增加了dx.于是,有关系式
,经过时间dt后,容器内物质A的质量增加了dx.于是,有关系式
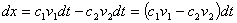
因为
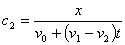
代入上式有
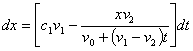
或

这是一个线性方程.求物质A在时刻t的质量的问题就归结为求方程满足初始条件x(0)= 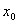 的解的问题.
的解的问题.
例: 某厂房容积为45m×15m×6m,经测定,空气中含有0.2﹪的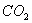 .开通通风设备,以360
.开通通风设备,以360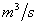 的速度输入含有0.05﹪的
的速度输入含有0.05﹪的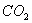 的新鲜空气,同时又排出同等数量的室内空气.问30min后室内所含
的新鲜空气,同时又排出同等数量的室内空气.问30min后室内所含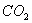 的百分比.
的百分比.
解 设在时刻t,车间内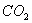 的百分比为x(t) ﹪,当时间经过dt后,室内
的百分比为x(t) ﹪,当时间经过dt后,室内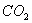 的该变量为
的该变量为
45×15×6×dx﹪=360×0.05﹪×dt-360×x﹪×dt
于是有关系式
4050dx=360(0.05-x)dt
或
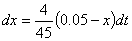
初值条件为x(0)=0.2.
将方程分离变量并积分,初值解满足
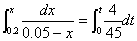
求出x,有
X=0.05+0.15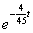
以t=30min=1800s代入,得x≈0.05.即开动通风设备30min后,室内的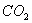 含量接近0.05﹪,基本上已是新鲜空气了.
含量接近0.05﹪,基本上已是新鲜空气了.
4.变化率问题
若某未知函数的变化率的表达式为已知,那么据此列出的方程常常是一阶微分方程.
例:在某一个人群中推广技术是通过其中已掌握新技术的人进行的,设该人群的总人数为N,在t=0时刻已掌握新技术的人数为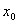 ,在任意时刻t已掌握新技术的人数为x(t)(将x(t)视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例系数k>0,求x(t).
,在任意时刻t已掌握新技术的人数为x(t)(将x(t)视为连续可微变量),其变化率与已掌握新技术人数和未掌握新技术人数之积成正比,比例系数k>0,求x(t).
解 由题意立即有
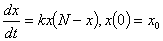
按分离变量法解之,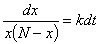 ,即
,即
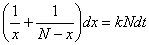
积分并化简的通解
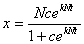
由初值条件得特解
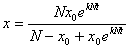
总结:通过以上几个简单的例子,我们发现用微分方程解决一些实际问题其实很方便,也很普遍,所以在以后的学习中,除了学习必须的理论与方法外,更应该加强理论与实际的联系,将学习的知识更好的用于解决实际问题中.
参考文献
[1] 欧阳瑞,孙要伟.常微分方程在数学建模中的应用[J].宿州教育学院学报,2008,11(2)
[2] 朱思铭 王高雄
王高雄 常微分方程[M],第三版
常微分方程[M],第三版 高等教育出版社
高等教育出版社 2006
2006
[3] 东北师范大学微分方程教研室.常微分方程,第二版.高等教育出版社.2005
[4] 蔡燧林,常微分方程,第二版.武汉大学出版社.2003.
