20xx年大学高数学习方法总结
一提起“数学”课,大家都会觉得再熟悉不过了,从小学一直到高中,它几乎就是一门陪伴着我们成长的学科。然而即使有着大学之前近XX年的数学学习生涯,仍然会有很多同学在初学大学数学时遇到很多困惑与疑问,更可能会有一种摸不着头脑的感觉。那么,究竟应该如何在大学中学好高数呢?
在中学的时候,可能许多同学都比较喜欢学习数学,而且数学成绩也很优秀,因而这时是处于一种良性循环的状态,不会有太多的挫败感,因而也就不会太在意勇于面对的重要性。而刚一进入大学,由于理论体系的截然不同,我们会在学习开始阶段遇到不小的麻烦,甚至会有不如意的结果出现,这时就一定得坚持住,能够知难而进,继续跟随老师学习。
很多同学在刚入学不久,就是一直感觉很晕。对于上课老师所讲的知识,虽然表面上能听懂,但却不明白知识背后的真正原因,所以总是感觉学到的东西不实在。至于做题就更差劲了,“吉米多维奇”上的习题根本不敢去看,因为书上的课后习题都没几个会做的。这确实与高中的情形相差太大了,香港浸会大学的杨涛教授曾经在一次讲座中讲过:“在初学高数时感觉晕是很正常的,而且还得再晕几个月可能就好了。”所以关键是不要放弃,初学者必须要克服这个困难才能学好大学理论知识。除了要坚持外,还要注意不要在某些问题的解决上花费过多的时间。因为大学数学理论十分严谨,教科书在讲解初步知识时,有时会不可避免地用到一些以后才能学到的理论思想,因而在初步学习时就对着这种问题不放是十分不划算的。
所以,在开始学习数学时,可以考虑采取迂回的学习方式。先把那些一时难以想通的问题记下,转而继续学习后续知识,然后不时地回头复习,在复习时由于后面知识的积累就可能会想通以前遗留的问题,进而又能促进后面知识的深刻理解。这种迂回式的学习方法,使得温故不但能知新,而且还能更好地知故。
第二篇:20xx年考研难题总结,(同济大学高数,线代 ,浙大).doc
20##年考研难题总结,(同济大学高数,线代 ,浙大)
( 2012.10整理)
一、填空:(本题15分,每空3分。请将最终结果填在相应的横杠上面。)
1. 函数 在(-∞,+∞)上连续,则a = 2 。
在(-∞,+∞)上连续,则a = 2 。
2. 设函数y = y(x) 由方程 所确定,则
所确定,则
 。
。
3. 由曲线 与x轴所围成的图形的面积A =
与x轴所围成的图形的面积A = 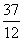 。
。
4. 设E为闭区间[0,4π]上使被积函数有定义的所有点的集合,则
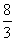 。
。
5.设L是顺时针方向的椭圆 ,其周长为l ,则
,其周长为l ,则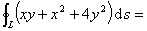 4l 。
4l 。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
1. 若 且
且 ,则( D )
,则( D )
(A) 存在; (B)
存在; (B) 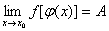
(C) 不存在; (D) A、B、C均不正确。
不存在; (D) A、B、C均不正确。
2. 设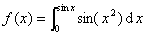 ,
, ,则当
,则当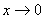 时,( A )
时,( A )
(A) 与
与 为同阶但非等价无穷小; (B)
为同阶但非等价无穷小; (B) 与
与 为等价无穷小;
为等价无穷小;
(C) 是比
是比 更高阶的无穷小; (D)
更高阶的无穷小; (D) 是比
是比 更低阶的无穷小。
更低阶的无穷小。
3. 设函数 对任意x都满足
对任意x都满足 ,且
,且 ,其中a、b均为非零常数,则
,其中a、b均为非零常数,则 在x = 1处( D )
在x = 1处( D )
(A)不可导; (B)可导,且 ;
;
(C)可导,且 ; (D)可导,且
; (D)可导,且 。
。
4. 设 为连续函数,且
为连续函数,且 不恒为零,I=
不恒为零,I= ,其中s > 0,t > 0,则I的值( C )
,其中s > 0,t > 0,则I的值( C )
(A)与s和t有关; (B)与s、t及x有关;
(C)与s有关,与t无关; (D)与t有关,与s无关。
5. 设u (x,y) 在平面有界闭区域D上具有二阶连续偏导数,且满足 及
及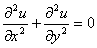 ,则( B )。
,则( B )。
(A)u (x,y) 的最大值点和最小值点必定都在区域D的内部;
(B)u (x,y) 的最大值点和最小值点必定都在区域D的边界上;
(C)u (x,y) 的最大值点在区域D的内部,最小值点在区域D的边界上;
(D)u (x,y) 的最小值点在区域D的内部,最大值点在区域D的边界上。
以下各题的解答写在试题纸上,可以不抄题,但必须写清题号,否则解答将被视为无效。
三、求极限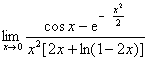 。(本题6分)
。(本题6分)
解: ;
;
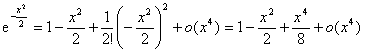 ;
;
 ;
;
由此得到:
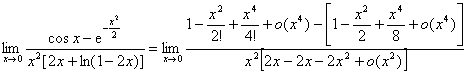
 。
。
四、计算 。(本题6分)
。(本题6分)
解: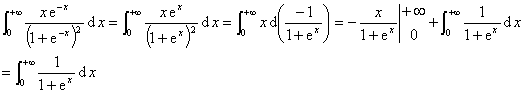
命: ,于是
,于是

五、设函数 的所有二阶偏导数都连续,
的所有二阶偏导数都连续,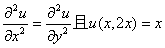 ,
, ,求
,求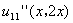 。(本题6分)
。(本题6分)
解: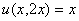 两边对x求导,得到
两边对x求导,得到

代入 ,求得
,求得  ,
,
 两边对x求导,得到
两边对x求导,得到  ,
,
 两边对x求导,得到
两边对x求导,得到  。
。
以上两式与已知 联立,又二阶导数连续,所以
联立,又二阶导数连续,所以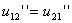 ,故
,故
 。
。
六、在具有已知周长2p的三角形中,怎样的三角形的面积最大?(本题7分)
解:设三角形的三条边长分别为x、y、z,由海伦公式知,三角形的面积S的平方为

则本题即要求在条件x + y + z = 2p之下S达到的最大值。它等价于在相同的条件下S2达到最大值。
设  ,
,
问题转化成求 在
在

上的最大值。其中D中的第3个条件是这样得到的,由于三角形的任意两边之和大于第三边,故有x + y > z,而由假设x + y + z = 2p,即 z = 2p-(x + y),故有x + y > z = 2p-(x + y),所以有x + y > p。
由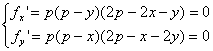 ,
,
求出 在D内的唯一驻点
在D内的唯一驻点 。因
。因 在有界闭区域
在有界闭区域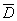 上连续,故
上连续,故 在
在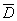 上有最大值。注意到
上有最大值。注意到 在
在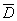 的边界上的值为0,而在D内的值大于0。故
的边界上的值为0,而在D内的值大于0。故 在D内取得它在
在D内取得它在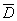 上的最大值。由于
上的最大值。由于 在D内的偏导数存在且驻点唯一,因此最大值必在点M处取得。于是有
在D内的偏导数存在且驻点唯一,因此最大值必在点M处取得。于是有
 ,
,
此时x = y = z = ,即三角形为等边三角形。
,即三角形为等边三角形。
七、计算 。(本题8分)
。(本题8分)
解:先从给定的累次积分画出积分区域图,再交换累次积分次序,得到
 。
。
八、计算曲面积分 ,其中Σ为上半球面
,其中Σ为上半球面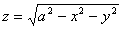 的上侧。(本题7分)
的上侧。(本题7分)
解:记S为平面z = 0( x2 + y2 ≤a2 )的下侧,Ω为Σ与S所围的空间区域,

九、已知a>0,x1>0,定义

求证: 存在,并求其值。(本题8分)
存在,并求其值。(本题8分)
解:第一步:证明数列 的极限存在:
的极限存在:
注意到:当n ≥ 2时, ≥
≥ ,因此数列
,因此数列 有下界。又
有下界。又 ≤
≤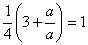 ,即xn+1≤xn ,所以
,即xn+1≤xn ,所以 单调递减,由极限存在准则知,数列
单调递减,由极限存在准则知,数列 有极限。
有极限。
第二步:求数列 的极限
的极限
设: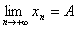 ,则有
,则有 ≥
≥ 。
。
由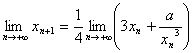 ,
,
有 ,解得
,解得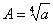 (舍掉负根),即
(舍掉负根),即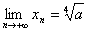 。
。
十、证明不等式 。(本题7分)
。(本题7分)
证明:设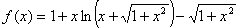 ,则
,则
 。
。
命 ,得到驻点 x = 0。由
,得到驻点 x = 0。由

可知 x = 0 为极小值点,亦即最小值点,最小值为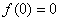 ,于是对任意
,于是对任意 有
有 ,即所证不等式成立。
,即所证不等式成立。
十一、设函数 在闭区间[0,1]上连续,在开区间(0,1)内可导,且
在闭区间[0,1]上连续,在开区间(0,1)内可导,且 ,求证:在开区间(0,1)内至少存在一点
,求证:在开区间(0,1)内至少存在一点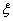 ,使得
,使得 。(本题7分)
。(本题7分)
证明:由积分中值定理知,存在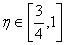 ,使得
,使得
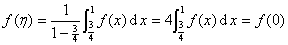
又函数 在区间
在区间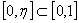 上连续,
上连续,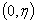 内可导,由罗尔定理知,至少存在一点
内可导,由罗尔定理知,至少存在一点 ,使得
,使得 。
。
十二、设 在区间
在区间 上具有二阶导数,且
上具有二阶导数,且 ,
, ,
, 。证明
。证明 。(本题8分)
。(本题8分)
证明:对任意的 ,及任意的h > 0,使x + h ∈ (a,+∞),于是有
,及任意的h > 0,使x + h ∈ (a,+∞),于是有
 ,其中
,其中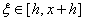 。
。
即 
故 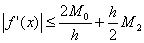 ,(
,( ,h > 0)
,h > 0)
命 ,试求其最小值。
,试求其最小值。
命 ,得到
,得到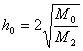 ,
,
 ,
,
所以, 在
在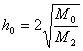 处得极小值,亦即最小值,
处得极小值,亦即最小值,
 。
。
故  ,(
,( )。
)。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1.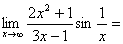
 。
。
2.设摆线方程为 则此曲线在
则此曲线在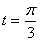 处的法线方程为
处的法线方程为 。
。
3.
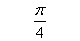 。
。
4.设 在点(-1,1)处沿方向
在点(-1,1)处沿方向 的方向导数
的方向导数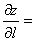
 。
。
5.设Σ为曲面 介于0≤Z≤R的部分,则
介于0≤Z≤R的部分,则 。
。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
1. 曲线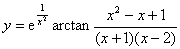 的渐近线有( B )
的渐近线有( B )
(A)1条; (B) 2条;
(C)3条; (D) 4条。
2. 若 ,则当n>2时
,则当n>2时 ( A )
( A )
(A) ; (B)
; (B) ;
;
(C)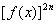 ; (D)
; (D) 。
。
3. 已知函数f (x)在(-∞,+∞)内有定义,且x0是函数f (x)的极大值点,则( C )
(A)x0是f (x)驻点; (B)在(-∞,+∞)内恒有f (x)≤f (x0);
(C)-x0是-f (-x)的极小值点; (D)-x0是-f (x)的极小值点。
4. 设 ,则z = z (x,y)在点(0,0)( D )
,则z = z (x,y)在点(0,0)( D )
(A)连续且偏导数存在; (B)连续但不可微;
(C)不连续且偏导数不存在; (D)不连续但偏导数存在。
5. 设 ,其中Ω:x2+y2+z2≤1,z≥0则
,其中Ω:x2+y2+z2≤1,z≥0则 ( D )
( D )
(A) ; (B)
; (B) ;
;
(C) ; (D)
; (D) 。
。
三、已知极限 ,试确定常数n和C的值。(本题6分)
,试确定常数n和C的值。(本题6分)
解: ,
,
故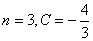 。
。
四、已知函数f (x)连续, ,求
,求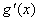 。(本题6分)
。(本题6分)
解:命u = t - x,则当 t = 0 时,u = -x;t = x 时,u = 0,于是

五、设方程 ,
,
⑴ 当常数a,b满足何种关系时,方程有唯一实根?
⑵ 当常数a,b满足何种关系时,方程无实根。(本题7分)
解:设 ,-∞<x<+∞,求导得
,-∞<x<+∞,求导得

命 得唯一驻点
得唯一驻点 ,又
,又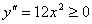 ,故当
,故当 时,y有最小值。且最小值为
时,y有最小值。且最小值为

又当x →-∞时,y →+∞;x →+∞时,y →+∞,因此,
⑴ 当且仅当 时,方程有唯一实根。
时,方程有唯一实根。
⑵ 当 时,方程无实根。
时,方程无实根。
六、在曲线y = x2(x ≥ 0)上某点A作一切线,使之与曲线及x轴所围图形的面积为 ,试求:
,试求:
⑴ A点的坐标;
⑵ 过切点A的切线方程;
⑶ 该图形绕x轴旋转一周所成旋转体的体积。(本题8分)
解:⑴设A点坐标为 (x0,y0),则y0 = x02,于是可知切线方程
y ― x02 = 2x0(x ― x0)即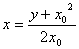 。
。
由题设,有

故有 。
。
⑵ 切线方程为 。
。
⑶ 在上述切线方程中令y = 0,得到 ,故所求旋转体的体积
,故所求旋转体的体积

七、计算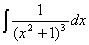 。(本题7分)
。(本题7分)
解:解法1
命 ,则有
,则有
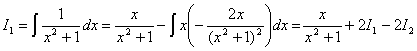 ,于是有
,于是有
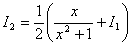 。
。
同理 ,
,
所以有
 。
。
解法2
命 ,则
,则
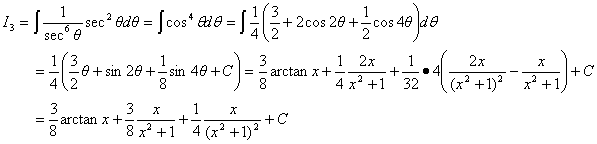
八、设 ,其中
,其中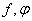 具有连续的一阶偏导数,且
具有连续的一阶偏导数,且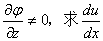 。(本题7分)
。(本题7分)
解:将y = sinx代入 ,得到
,得到 ,显然方程
,显然方程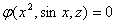 确定了 z 是x 的隐含数 z = z (x) ,所以
确定了 z 是x 的隐含数 z = z (x) ,所以

又由  ,
,
得到  。
。
九、求 上的最大值与最小值。(本题7分)
上的最大值与最小值。(本题7分)
解:解法1
在S上有 ,代入
,代入 ,得到
,得到
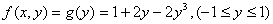
因此 
命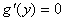 ,得到
,得到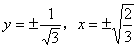 ,
,
由于 ,
,
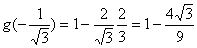 ,又
,又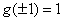 ,所以
,所以
 ;
;
 。
。
解法2
构造 ,
,
解方程组

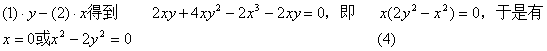
联合求解(3)、(4),得到6个可能的极值点
 ,
,
因为 ,所以
,所以
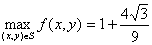 ,
, 。
。
十、计算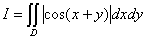 ,其中区域D为:
,其中区域D为: 。(本题7分)
。(本题7分)
解:如图,用直线 将区域D分为D1和D2两个区域,则
将区域D分为D1和D2两个区域,则


十一、证明:当 0 < x < 1时,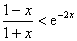 。(本题7分)
。(本题7分)
证明:本题即证当0 < x < 1时,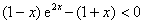 ,命:
,命: ,于是有
,于是有
 ,
,
 ,
,
即 在区间(0,1)内单调减少,而
在区间(0,1)内单调减少,而 ,故当 x > 0时
,故当 x > 0时 ,因而
,因而 在区间(0,1)内单调减少,即
在区间(0,1)内单调减少,即 ,于是有
,于是有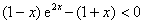 ,即
,即 。
。
十二、设C是取正向的圆周 ,f (x)是正的连续函数,证明:
,f (x)是正的连续函数,证明:

(本题8分)
证明:由格林公式有
 ,
,
其中D是由 ( x – 1 )2 + ( y – 1 )2 = 1所围成的区域。而
 ,
,
 ,
,
即  ,
,
所以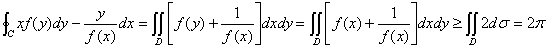 。
。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1.设对一切实数x和y,恒有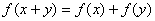 ,且知
,且知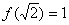 ,则
,则
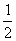 。
。
2.设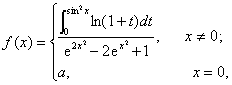 在x = 0处连续,则a =
在x = 0处连续,则a = 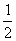 。
。
3.设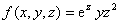 ,其中
,其中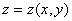 是由方程
是由方程 所确定的隐函数,则
所确定的隐函数,则
 。
。
4.
 。
。
5.曲线 在点M (1,1,1)处的切线方程为
在点M (1,1,1)处的切线方程为 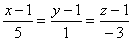 (或
(或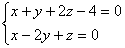 )。
)。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
1. 当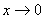 时,下列无穷小量
时,下列无穷小量
①  ; ②
; ② 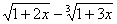 ;
;
③  ; ④
; ④  ,
,
从低阶到高阶的排列顺序为( D )
(A)①②③④; (B) ③①②④;
(C)④③②①; (D) ④②①③。
2. 设 ,在x = 0处存在最高阶导数的阶数为( B )
,在x = 0处存在最高阶导数的阶数为( B )
(A) 1阶; (B) 2阶; (C) 3阶; (D)4阶。
3. 设函数 在 x = 1处有连续的导函数,又
在 x = 1处有连续的导函数,又 ,则x = 1是( B )
,则x = 1是( B )
(A)曲线 拐点的横坐标; (B)函数
拐点的横坐标; (B)函数 的极小值点;
的极小值点;
(C)函数 的极大值点; (D)以上答案均不正确。
的极大值点; (D)以上答案均不正确。
4. 设函数f,g在区间[a,b]上连续,且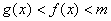 (m为常数),则曲线
(m为常数),则曲线 和x = b所围平面图形绕直线y = m旋转而成的旋转体体积为( A )
和x = b所围平面图形绕直线y = m旋转而成的旋转体体积为( A )
(A)  ; (B)
; (B) 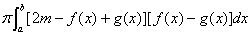 ;
;
(C) 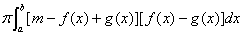 ; (D)
; (D) 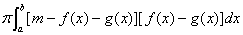 。
。
5. 设 ,
,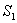 为
为 在第一卦限中的部分,则有( C )
在第一卦限中的部分,则有( C )
(A) ; (B)
; (B) ;
;
(C) ; (D)
; (D)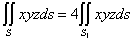 。
。
三、a,b,c为何值时,下式成立
 。
。
(本题6分)
解:注意到左边的极限中,无论a为何值总有分母趋于零,因此要想极限存在,分子必须为无穷小量,于是可知必有b= 0,当b= 0时使用诺必达法则得到
 ,
,
由上式可知:当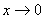 时,若
时,若 ,则此极限存在,且其值为0;若a = 1,则
,则此极限存在,且其值为0;若a = 1,则
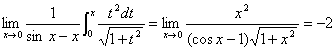 。
。
综上所述,得到如下结论: ,b = 0,c = 0;
,b = 0,c = 0;
或a = 1,b = 0,c = -2。
四、设函数 ,其中
,其中 具有连续二阶导函数,且
具有连续二阶导函数,且 。
。
⑴ 确定a的值,使 在点x = 0处可导,并求
在点x = 0处可导,并求 。
。
⑵ 讨论 在点x = 0处的连续性。(本题8分)
在点x = 0处的连续性。(本题8分)
解:⑴ 欲使 在点x = 0处可导,
在点x = 0处可导, 在点x = 0处必须连续,于是有
在点x = 0处必须连续,于是有

即当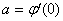 时,
时, 在点x = 0处连续。
在点x = 0处连续。
当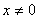 时,
时,
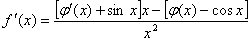 ;
;
当x = 0时,
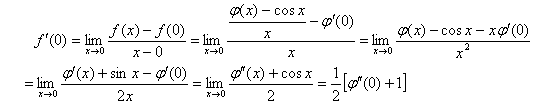
故:
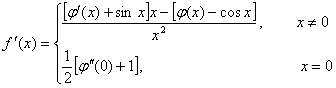 。
。
⑵ 因为

所以, 在点x = 0处连续。
在点x = 0处连续。
五、设正值函数 在
在 上连续,求函数
上连续,求函数 的最小值点。(本题6分)
的最小值点。(本题6分)
解:
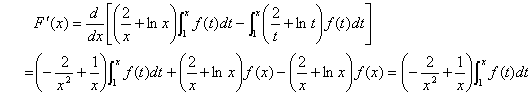
注意到:在 上
上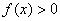 ,因此,当x > 1时,
,因此,当x > 1时,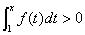 。
。
命: ,得
,得 ,解此方程得到唯一驻点 x = 2。
,解此方程得到唯一驻点 x = 2。
又,当 时,
时,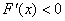 ;当x > 2时,
;当x > 2时, ,所以
,所以 在点x = 2处取得极小值
在点x = 2处取得极小值 ,又因为x = 2是唯一的极值点,所以x = 2是
,又因为x = 2是唯一的极值点,所以x = 2是 的最小值点,最小值为
的最小值点,最小值为 。
。
六、设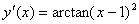 ,且
,且 ,求
,求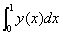 。(本题6分)
。(本题6分)
解:

七、设变换 ,把方程
,把方程 化为
化为 ,试确定a。(本题7分)
,试确定a。(本题7分)
解: 计算一、二阶偏导数
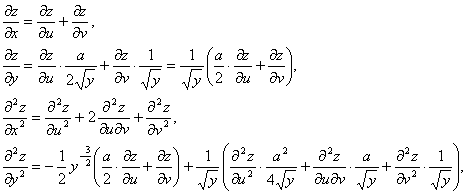
代入方程 ,得到
,得到
 ,
,
于是有 ,所以
,所以 。
。
八、设函数 在x O y平面上具有连续一阶偏导数,曲线积分
在x O y平面上具有连续一阶偏导数,曲线积分 与路径无关,并且对任意的t恒有
与路径无关,并且对任意的t恒有 ,求
,求 。(本题7分)
。(本题7分)
解:由曲线积分与路径无关知
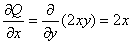 ,
,
所以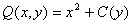 ,其中
,其中 为待定函数。又
为待定函数。又
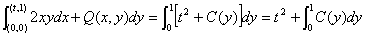 ;
;
 。
。
根据题设,有
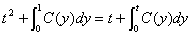 ,
,
上式两边对t求导,得到
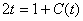 ,于是知
,于是知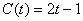 ,即
,即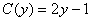 ,故
,故 。
。
九、设函数f (x)具有二阶连续导函数,且 。在曲线y = f (x)上任意取一点
。在曲线y = f (x)上任意取一点 作曲线的切线,此切线在x轴上的截距记作
作曲线的切线,此切线在x轴上的截距记作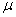 ,求
,求 。(本题8分)
。(本题8分)
解: 过点 的曲线y = f (x)的切线方程为:
的曲线y = f (x)的切线方程为: ,
,
注意到:由于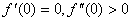 ,所以当
,所以当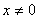 时,
时, 。因此,此直线在x轴上的截距为
。因此,此直线在x轴上的截距为
 。且
。且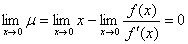 。
。
利用泰勒公式将 在
在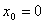 点处展开,得到
点处展开,得到
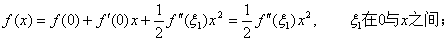 。
。
类似可得: 。代入得
。代入得
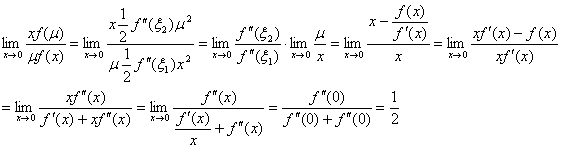
十、设函数f (x)在闭区间 上连续,在开区间 (0,1) 内可导,且f ( 0 ) = 0,f ( 1 ) = 1 。试证明:对于任意给定的正数a和b,在开区间 (0,1) 内存在不同的ξ和η,使得
上连续,在开区间 (0,1) 内可导,且f ( 0 ) = 0,f ( 1 ) = 1 。试证明:对于任意给定的正数a和b,在开区间 (0,1) 内存在不同的ξ和η,使得
 。
。
(本题7分)
证明:取数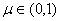 ,由连续函数介值定理知,存在
,由连续函数介值定理知,存在 ,使得
,使得 。在区间[0,C]与[C,1]上分别应用拉格朗日中值定理,有
。在区间[0,C]与[C,1]上分别应用拉格朗日中值定理,有
 显然
显然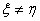 。
。
由于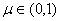 ,所以
,所以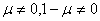 ,即
,即 。从而
。从而
 ,
,
注意到:若取 ,则
,则 ,并且
,并且 ,代入得
,代入得
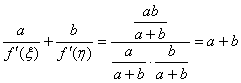 。
。
十一、设 ,试证明在区间
,试证明在区间 上
上 有且仅有两个实根。(本题7分)
有且仅有两个实根。(本题7分)
证明:

由于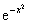 是偶函数,所以
是偶函数,所以 是奇函数,
是奇函数, 是偶函数,于是知
是偶函数,于是知 为偶函数。
为偶函数。
又注意到:

 ,(当x > 0时)。
,(当x > 0时)。
因此,函数 在闭区间[0,1]上有且仅有唯一一个实根;又
在闭区间[0,1]上有且仅有唯一一个实根;又 为偶函数,所以
为偶函数,所以 在闭区间
在闭区间 上同样有且仅有唯一一个实根。于是知函数
上同样有且仅有唯一一个实根。于是知函数 在闭区间
在闭区间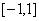 上有且仅有两个实根。
上有且仅有两个实根。
十二、设函数 在单位圆域上有连续的偏导数,且在边界上的值恒为零。证明:
在单位圆域上有连续的偏导数,且在边界上的值恒为零。证明:

其中:D为圆域 。(本题8分)
。(本题8分)
证明:取极坐标系,由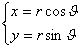 ,得到
,得到
 ,
,
将上式两端同乘r,得到
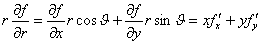 。
。
于是有
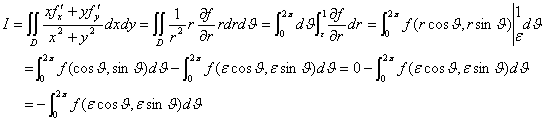
由积分中值定理,有
 ,其中
,其中 。
。
故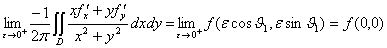 。
。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1.设函数 ,则函数
,则函数 的定义域为
的定义域为 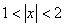 。
。
2.设要使函数 在区间
在区间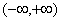 上连续,则
上连续,则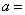
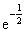 。
。
3.设函数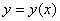 由参数方程
由参数方程 所确定,其中f可导,且
所确定,其中f可导,且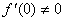 ,则
,则 3 。
3 。
4.由方程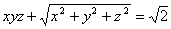 所确定的函数
所确定的函数 在点
在点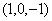 处的全微分dz =
处的全微分dz = 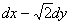 。
。
5.设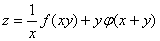 ,其中 f 、
,其中 f 、 具有二阶连续导数,则
具有二阶连续导数,则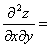
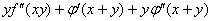 。
。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
6. 已知 ,则
,则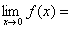 ( A )
( A )
(A)12; (B)3; (C)1; (D)0。
7. 设函数 在
在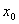 的一个邻域内有定义,则在
的一个邻域内有定义,则在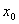 点处存在连续函数
点处存在连续函数 使
使 是
是 在
在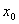 点处可导的( C )
点处可导的( C )
(A)充分而非必要条件; (B)必要而非充分条件;
(C)充分必要条件; (D)既非充分,也非必要条件。
8. 设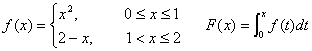 ,则F(x)=( D )
,则F(x)=( D )
(A)  ; (B)
; (B)  ;
;
(C)  ; (D)
; (D)  。
。
9. 函数 ,在点
,在点 处
处 ( B )
( B )
(A)可微; (B)偏导数存在,但不可微;
(C)连续,但偏导数不存在; (D)不连续且偏导数不存在。
10. 设 为区间
为区间 上的正值连续函数,
上的正值连续函数, 与
与 为任意常数,区域
为任意常数,区域 ,则
,则 ( D )
( D )
(A) ; (B)
; (B) ; (C)
; (C) ; (D)
; (D) 。
。
三、设函数 在点
在点 的某邻域内具有二阶导数,且
的某邻域内具有二阶导数,且
 。
。
求: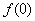 ,
, ,
, 及
及 。(本题6分)
。(本题6分)
解:因为  ,
,
所以  。
。
由无穷小比较,可知  ,
,
以及 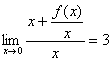 。
。
从而 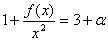 ,其中
,其中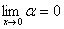 ,
,
即  。
。
由此可得  ,
,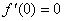 ,
, 。
。
并有 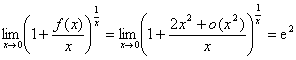 。
。
四、计算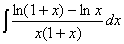 。(本题6分)
。(本题6分)
解:

五、求函数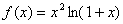 在
在 点处的100阶导数值。(本题6分)
点处的100阶导数值。(本题6分)
解:方法一:利用莱布尼兹公式
 ,
,
又

由归纳法可得 。
。
故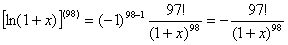 。
。
所以 。
。
方法二:利用泰勒公式
 ,故
,故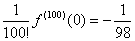 ,
, 。
。
六、设 为定义在
为定义在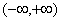 上,以T > 0为周期的连续函数,且
上,以T > 0为周期的连续函数,且 。求
。求 。(本题7分)
。(本题7分)
解:对于充分大的x > 0,必存在正整数n,使得
 。
。
又  ,
,
故有 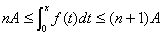 ,
,
及  。
。
注意到:  ,
,
且当 时,
时,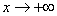 。由夹逼定理可知
。由夹逼定理可知
 。
。
七、在椭球面 上求一点,使函数
上求一点,使函数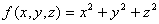 在该点沿方向
在该点沿方向 的方向导数最大。(本题8分)
的方向导数最大。(本题8分)
解: 函数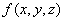 的方向导数的表达式为
的方向导数的表达式为
 。
。
其中: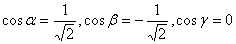 为方向
为方向 的方向余弦。因此
的方向余弦。因此
 。
。
于是,按照题意,即求函数 在条件
在条件 下的最大值。设
下的最大值。设
 ,
,
则由

得 以及
以及 ,即得驻点为
,即得驻点为 与
与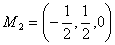 。
。
因最大值必存在,故只需比较
 ,
, ,
,
的大小。由此可知 为所求。
为所求。
八、设正整数 ,证明方程
,证明方程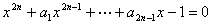 至少有两个实根。(本题6分)
至少有两个实根。(本题6分)
证明:设 ,则其在区间
,则其在区间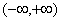 上连续,且
上连续,且 ,
, 。
。
因而,当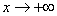 时,必存在
时,必存在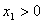 ,使得
,使得 。由连续函数的介值定理可知,至少有一点
。由连续函数的介值定理可知,至少有一点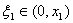 ,使得
,使得 。
。
同理,当 时,必存在
时,必存在 ,使得
,使得 。由连续函数的介值定理可知,至少有一点
。由连续函数的介值定理可知,至少有一点 ,使得
,使得 。
。
综上可知,方程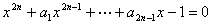 至少有两个实根。
至少有两个实根。
九、设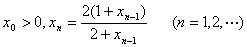 。证明
。证明 存在,并求之。(本题8分)
存在,并求之。(本题8分)
证明: 证明 存在:
存在:
注意到:对于一切的n恒有
 ,
,
 ,
,
因此知数列 有界。又
有界。又
 ,
,
 ,……,
,……,
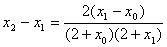 ,
,
于是可知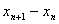 与
与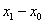 同号,故当
同号,故当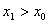 时,数列
时,数列 单调递增;当
单调递增;当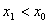 时,数列
时,数列 单调递减。也就是说,数列
单调递减。也就是说,数列 为单调有界数列,而单调有界数列必有极限。
为单调有界数列,而单调有界数列必有极限。
求 :
:
设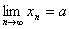 ,则
,则
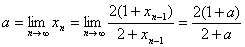 ,
,
解之得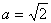 ,即
,即 。
。
十、计算曲面积分 ,其中
,其中 是曲线
是曲线 绕z轴旋转而成的旋转面,其法线向量与z轴正向的夹角为锐角。(本题7分)
绕z轴旋转而成的旋转面,其法线向量与z轴正向的夹角为锐角。(本题7分)
解: 旋转曲面的方程为 。补充曲面
。补充曲面
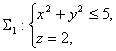 其法线向量与z轴正向相反;和
其法线向量与z轴正向相反;和
 其法线向量与z轴正向相同。
其法线向量与z轴正向相同。
设由曲面 所围空间区域为
所围空间区域为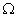 ,则
,则
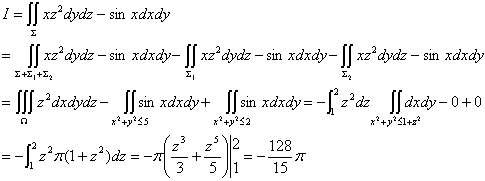
十一、设 具有连续的偏导数,且对以任意点
具有连续的偏导数,且对以任意点 为圆心,以任意正数r为半径的上半圆L:
为圆心,以任意正数r为半径的上半圆L: ,恒有
,恒有
 。
。
证明: (本题8分)
(本题8分)
证明:记上半圆周L的直径为AB,取AB+L为逆时针方向;又命D为AB+L所包围的区域。由格林公式有

其中: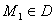 为某一点。另一方面
为某一点。另一方面
 。
。
于是有
 ,
,
即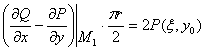 。
。
命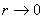 ,两边取极限,得到
,两边取极限,得到 ,由
,由 的任意性知
的任意性知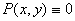 ;且
;且
 ,即
,即 。
。
类似 。
。
十二、设函数 在[0,1]上连续,且
在[0,1]上连续,且 ,试证:
,试证:
⑴ ,使得
,使得 ;
;
⑵ ,使得
,使得 。(本题8分)
。(本题8分)
证明: ⑴ 使用反证法,即假设当 时,恒有
时,恒有 成立,于是有
成立,于是有
 。
。
因此有 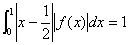 ,
, 。
。
从而有 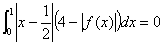 。
。
于是有 ,即
,即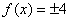 ,这显然与
,这显然与 矛盾,故
矛盾,故 ,使得
,使得 为真。
为真。
⑵ 仍然使用反证法。
只需证 ,使得
,使得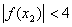 即可。这是显然的,因为若不然,则由
即可。这是显然的,因为若不然,则由 在[0,1]上的连续性知,必有
在[0,1]上的连续性知,必有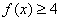 或
或 成立,这与
成立,这与 矛盾,再由
矛盾,再由 的连续性及⑴的结果,利用介值定理即可证得
的连续性及⑴的结果,利用介值定理即可证得 ,使得
,使得 。
。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1.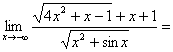 1 。
1 。
2.曲线 ,在点
,在点 处的法线方程为 2x+y-1=0 。
处的法线方程为 2x+y-1=0 。
3.设 为连续函数,且
为连续函数,且 ,则
,则
 。
。
4.函数 在点
在点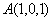 处,沿点A指向点
处,沿点A指向点 方向的方向导数为
方向的方向导数为  。
。
5.设(a×b)·c = 2,则[(a+b)×(b+c)]·(c+a)= 4 。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
11. 设函数 与
与 在开区间(a,b)内可导,考虑如下的两个命题,
在开区间(a,b)内可导,考虑如下的两个命题,
⑴ 若 ,则
,则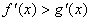 ;
;
⑵ 若 ,则
,则 。
。
则( B )
(A)两个命题均正确; (B)两个命题均不正确;
(C)命题⑴正确,命题⑵不正确; (D)命题⑴不正确,命题⑵正确。
12. 设函数 连续,F(x)是
连续,F(x)是 的原函数,则( A )
的原函数,则( A )
(A) 当 为奇函数时,F(x)必为偶函数;
为奇函数时,F(x)必为偶函数;
(B) 当 为偶函数时,F(x)必为奇函数;
为偶函数时,F(x)必为奇函数;
(C) 当 为周期函数时,F(x)必为周期函数;
为周期函数时,F(x)必为周期函数;
(D) 当 为单调递增函数时,F(x)必为单调递增函数。
为单调递增函数时,F(x)必为单调递增函数。
13. 设平面 位于平面
位于平面 :
: 与平面
与平面 :
: 之间,且将此两平面的距离分为1:3,则平面
之间,且将此两平面的距离分为1:3,则平面 的一个方程为( D )
的一个方程为( D )
(A) ; (B)
; (B) ;
;
(C)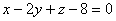 ; (D)
; (D) 。
。
14. 设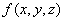 为非零的连续函数,
为非零的连续函数, ,则当t→0时( C )
,则当t→0时( C )
(A) 与t为同阶无穷小; (B)
与t为同阶无穷小; (B) 与t2为同阶无穷小;
与t2为同阶无穷小;
(C) 与t3为同阶无穷小; (D)
与t3为同阶无穷小; (D) 是比t3高阶的无穷小。
是比t3高阶的无穷小。
15. 设函数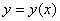 满足等式
满足等式 ,且
,且 ,则
,则 在点
在点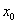 处( A )。
处( A )。
(A)取得极小值; (B)取得极大值;
(C)在点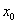 的一个邻域内单调增加; (D)在点
的一个邻域内单调增加; (D)在点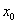 的一个邻域内单调减少。
的一个邻域内单调减少。
三、求函数 的值域。(本题6分)
的值域。(本题6分)
解:要求 的值域,只需求出函数的最大值与最小值即可。注意到:函数
的值域,只需求出函数的最大值与最小值即可。注意到:函数 为偶函数,故只需考虑x≥0的情况。为计算方便,命t=x2,得到
为偶函数,故只需考虑x≥0的情况。为计算方便,命t=x2,得到
 ,
,
显然, 与
与 有相同的值域。求
有相同的值域。求 的驻点:
的驻点:
 。
。
命 ,得到驻点
,得到驻点 ,其对应的函数值为
,其对应的函数值为
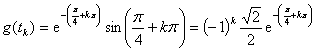 ,
,
显然,当k=2m(m=0,1,2,…)时, ,其中最大值为
,其中最大值为 ;当k=2m+1 (m=0,1,2,…)时,
;当k=2m+1 (m=0,1,2,…)时, ,其中最小值为
,其中最小值为 。于是得到函数
。于是得到函数 的值域,亦即函数
的值域,亦即函数 的值域为:
的值域为: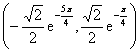 。
。
四、设 ,其中f具有二阶连续偏导数,g具有二阶连续导数。求
,其中f具有二阶连续偏导数,g具有二阶连续导数。求 。(本题6分)
。(本题6分)
解: ,
,
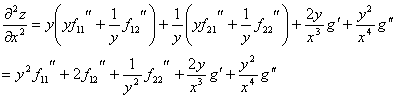
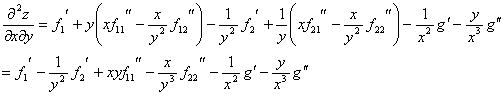
五、设二元函数 在有界闭区域D上可微,在D的边界曲线上
在有界闭区域D上可微,在D的边界曲线上 ,并满足
,并满足 ,求
,求 的表达式。(本题6分)
的表达式。(本题6分)
解:显然 满足题目条件。下面证明只有
满足题目条件。下面证明只有 满足题目条件。
满足题目条件。
事实上,若 不恒等于0,则至少存在一点
不恒等于0,则至少存在一点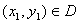 ,使得
,使得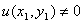 ,不妨假设
,不妨假设 ,同时,也必在D内至少存在一点
,同时,也必在D内至少存在一点 ,使
,使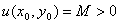 为
为 在D上的最大值。因为
在D上的最大值。因为 在D上可微,所以必有
在D上可微,所以必有 ,于是得到
,于是得到
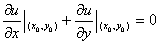 。
。
然而,由题设知 ,因此应有
,因此应有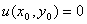 ,这与
,这与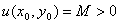 的假设矛盾;同理可证:
的假设矛盾;同理可证: 的情况。
的情况。
因此可知在D上 。
。
六、设二元函数 具有一阶连续偏导数,且
具有一阶连续偏导数,且 ,求
,求 。(本题7分)
。(本题7分)
解:注意到:被积函数 ,由于此积分与路径无关,所以必有
,由于此积分与路径无关,所以必有
 ,即有
,即有 ,
,
从而有 ,代入原积分式,得到
,代入原积分式,得到
 ,
,
即  ,
,
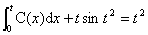 。
。
将上式两端对t求导,得到: 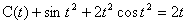 ,
,
即  ,
,
从而得到  。
。
七、设曲线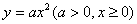 与
与 交于点A,过坐标原点O和点A的直线与曲线
交于点A,过坐标原点O和点A的直线与曲线 围成一平面图形,试问:
围成一平面图形,试问:
⑴ 当a为何值时,该图形绕x轴一周所得的旋转体体积最大?
⑵ 最大体积为多少?(本题7分)
解:当x≥0时,由 ,解得A点的坐标为
,解得A点的坐标为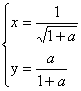 ,故直线OA的方程为
,故直线OA的方程为 。
。
于是,平面图形绕x轴一周所得的旋转体体积为:
 。
。
上式两边对a求导: 。
。
命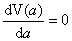 ,得到a=4。由于a=4是当
,得到a=4。由于a=4是当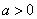 时
时 的唯一驻点,且由问题的实际意义可知存在最大体积,故
的唯一驻点,且由问题的实际意义可知存在最大体积,故 在a=4时取最大值。其最大体积为:
在a=4时取最大值。其最大体积为:
 。
。
八、设S为椭球面 的上半部分,点
的上半部分,点 ,
, 为S在点P处的切平面,
为S在点P处的切平面,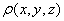 为点
为点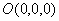 到平面
到平面 的距离,求
的距离,求 。(本题7分)
。(本题7分)
解:设 为
为 上任意一点,则
上任意一点,则 的方程为
的方程为
 ,
,
从而知
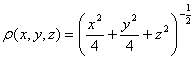 。
。
由 ,有
,有
 ,
,
于是  。
。
所以 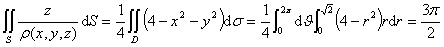 。
。
九、证明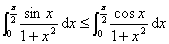 。(本题8分)
。(本题8分)
证明:方法一(利用积分估值定理)
命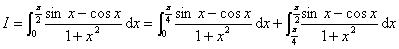 ,
,
对上式右端的第二个积分,取变换 ,则
,则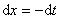 ,于是
,于是

注意到:被积函数的两个因子在区间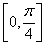 上异号(
上异号( ,
,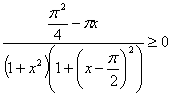 ),由积分估值定理得知必有I≤0,即知原不等式成立。
),由积分估值定理得知必有I≤0,即知原不等式成立。
方法二(利用积分中值定理)
命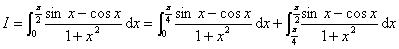 ,
,
由积分中值定理,并在区间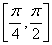 上取变换
上取变换 ,同时注意到:
,同时注意到: ,得
,得
十、设正值函数 在闭区间[a,b]上连续,
在闭区间[a,b]上连续, ,证明:
,证明:
 。
。
(本题8分)
证明:化为二重积分证明。记 ,则原式
,则原式
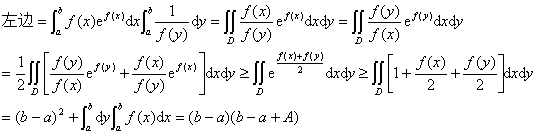
十一、设函数 在闭区间[a,b]上具有连续的二阶导数,证明:存在ξ∈(a,b),使得
在闭区间[a,b]上具有连续的二阶导数,证明:存在ξ∈(a,b),使得
 。
。
(本题7分)
证明:将函数 在点
在点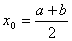 处作泰勒展开,并分别取x=a和b,得到
处作泰勒展开,并分别取x=a和b,得到
 ;
;
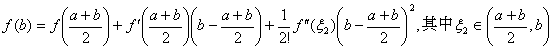 。
。
两式相加得到
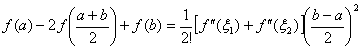 。
。
由于 连续,由介值定理知,存在
连续,由介值定理知,存在 使得
使得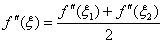 ,从而得
,从而得
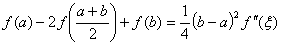 ,
,
即 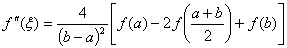 。
。
十二、设函数 在闭区间[-2,2]上具有二阶导数,
在闭区间[-2,2]上具有二阶导数, ,且
,且 ,证明:存在一点ξ∈(-2,2),使得
,证明:存在一点ξ∈(-2,2),使得 。(本题8分)
。(本题8分)
证明:在区间[-2,0]和[0,2]上分别对函数 应用拉格朗日中值定理
应用拉格朗日中值定理
 ;
;
 。
。
注意到: ,因此
,因此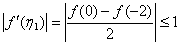 ,
, 。
。
命: ,则
,则 在区间[-2,2]上可导,且
在区间[-2,2]上可导,且
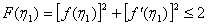 ;
;
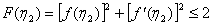 ;
;
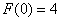 。
。
故 在闭区间
在闭区间 上的最大值
上的最大值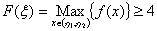 ,且
,且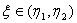 。由弗马定理知
。由弗马定理知 。而
。而  ,
,
故 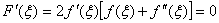 。
。
由于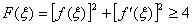 ,所以
,所以 ,从而
,从而 。
。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1.若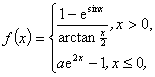 是
是 上的连续函数,则a = -1 。
上的连续函数,则a = -1 。
2.函数 在区间
在区间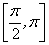 上的最大值为
上的最大值为 。
。
3.
 。
。
4.由曲线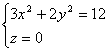 绕y轴旋转一周得到的旋转面在点
绕y轴旋转一周得到的旋转面在点 处的指向外侧的单位法向量为
处的指向外侧的单位法向量为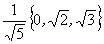 。
。
5.设函数 由方程
由方程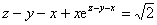 所确定,则
所确定,则
 。
。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
16. 设函数f (x)可导,并且 ,则当
,则当 时,该函数在点
时,该函数在点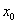 处微分dy是
处微分dy是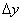 的( A )
的( A )
(A)等价无穷小; (B)同阶但不等价的无穷小;
(C)高阶无穷小; (D)低阶无穷小。
17. 设函数f (x)在点x = a处可导,则 在点x = a处不可导的充要条件是( C )
在点x = a处不可导的充要条件是( C )
(A)f (a) = 0,且 ; (B)f (a)≠0,但
; (B)f (a)≠0,但 ;
;
(C)f (a) = 0,且 ; (D)f (a)≠0,且
; (D)f (a)≠0,且 。
。
18. 曲线 ( B )
( B )
(A)没有渐近线; (B)有一条水平渐近线和一条斜渐近线;
(C)有一条铅直渐近线; (D)有两条水平渐近线。
19. 设 均为可微函数,且
均为可微函数,且 。已知
。已知 是
是 在约束条件
在约束条件 下的一个极值点,下列选项中的正确者为( D )
下的一个极值点,下列选项中的正确者为( D )
(A)若 ,则
,则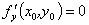 ; (B)若
; (B)若 ,则
,则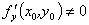 ;
;
(C)若 ,则
,则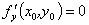 ; (D)若
; (D)若 ,则
,则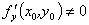 。
。
20. 设曲面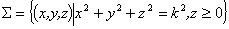 的上侧,则下述曲面积分不为零的是( B )
的上侧,则下述曲面积分不为零的是( B )
(A) ; (B)
; (B) ;
;
(C)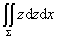 ; (D)
; (D) 。
。
三、设函数f (x)具有连续的二阶导数,且 ,
, ,求
,求 。(本题6分)
。(本题6分)
解:由题设可推知f (0) = 0, ,于是有
,于是有
 。
。
故  。
。
四、设函数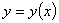 由参数方程
由参数方程 所确定,求
所确定,求 。(本题6分)
。(本题6分)
解:由 ,
, ,得到
,得到 ,所以
,所以
 。
。
而当x = 9时,由 及t > 1,得t = 2,故
及t > 1,得t = 2,故
 。
。
五、设n为自然数,计算积分 。(本题7分)
。(本题7分)
解:注意到:对于每个固定的n,总有
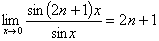 ,
,
所以被积函数在x = 0点处有界(x = 0不是被积函数的奇点)。又
 ,
,
于是有
 ,
,
上面的等式对于一切大于1的自然数均成立,故有 。所以
。所以
 。
。
六、设f (x)是除x = 0点外处处连续的奇函数,x = 0为其第一类跳跃间断点,证明 是连续的偶函数,但在x = 0点处不可导。(本题7分)
是连续的偶函数,但在x = 0点处不可导。(本题7分)
证明:因为x = 0是f (x)的第一类跳跃间断点,所以 存在,设为A,则A≠0;又因f (x)为奇函数,所以
存在,设为A,则A≠0;又因f (x)为奇函数,所以 。
。
命:

则 在x = 0点处连续,从而
在x = 0点处连续,从而 在
在 上处处连续,且
上处处连续,且 是奇函数:
是奇函数:
当x > 0,则-x < 0, ;
;
当x < 0,则-x > 0, ,
,
即 是连续的奇函数,于是
是连续的奇函数,于是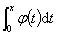 是连续的偶函数,且在x = 0点处可导。又
是连续的偶函数,且在x = 0点处可导。又
 ,
,
即  ,
,
所以 是连续的偶函数,但在x = 0点处不可导。
是连续的偶函数,但在x = 0点处不可导。
七、设f (u, v)有一阶连续偏导数, ,
, ,证明:
,证明:
 。
。
(本题7分)
解: 设: ,则
,则

类似可得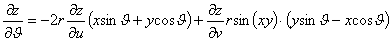 ,
,
代入原式左边,得到

八、设函数f (u)连续,在点u = 0处可导,且f(0)= 0, 求:
求: 。(本题7分)
。(本题7分)
解:记 ,应用球坐标,并同时注意到积分区域与被积函数的对称性,有
,应用球坐标,并同时注意到积分区域与被积函数的对称性,有

于是有
 。
。
九、计算 ,其中L为
,其中L为 正向一周。(本题7分)
正向一周。(本题7分)
解:因为L为 ,故
,故

其中D为L所围区域,故 为D的面积。为此我们对L加以讨论,用以搞清D的面积。
为D的面积。为此我们对L加以讨论,用以搞清D的面积。
当 时,
时,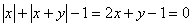 ;
;
当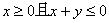 时,
时,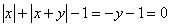 ;
;
当 时,
时, ;
;
当 时,
时, ,
,
故D的面积为2×1=2。从而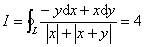 。
。
十、⑴ 证明:当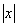 充分小时,不等式
充分小时,不等式 成立。
成立。
⑵ 设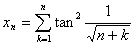 ,求
,求 。(本题8分)
。(本题8分)
证明:⑴ 因为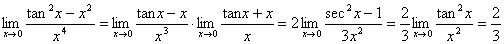 ,
,
又注意到当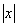 充分小时,
充分小时, ,所以成立不等式
,所以成立不等式 。
。
⑵ 由⑴知,当n充分大时有,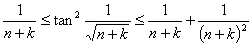 ,故
,故
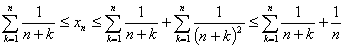 ,
,
而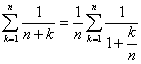 ,于是
,于是
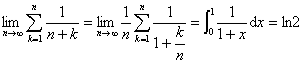 ,
,
由夹逼定理知 。
。
十一、设常数 ,证明:当x > 0且x≠ 1时,
,证明:当x > 0且x≠ 1时, 。(本题8分)
。(本题8分)
证明:设函数 ,
,
故要证 ,
,
只需证:当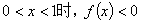 ;当
;当 。
。
显然: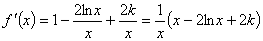 。
。
命: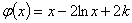 ,则
,则 。
。
当x = 2时,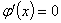 ,x = 2为唯一驻点。又
,x = 2为唯一驻点。又 ,
, ,所以x = 2为
,所以x = 2为 的唯一极小值点,故
的唯一极小值点,故 为
为 的最小值(x > 0),即当x > 0时
的最小值(x > 0),即当x > 0时 ,从而
,从而 严格单调递增。
严格单调递增。
又因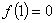 ,所以当
,所以当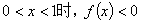 ;当
;当 。
。
十二、设匀质半球壳的半径为R,密度为μ,在球壳的对称轴上,有一条长为l的均匀细棒,其密度为ρ。若棒的近壳一端与球心的距离为a,a > R ,求此半球壳对棒的引力。(本题7分)
解:设球心在坐标原点上,半球壳为上半球面,细棒位于正z轴上,则由于对称性,所求引力在x轴与y轴上的投影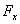 及
及 均为零。
均为零。
设k为引力常数,则半球壳对细棒引力在z轴方向的分量为:
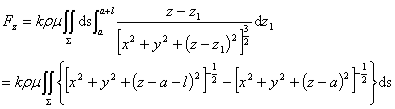
记 。在球坐标下计算
。在球坐标下计算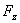 ,得到
,得到

若半球壳仍为上半球面,但细棒位于负z轴上,则
 。
。
20##年天津市大学数学竞赛试题参考答案
(理工类)
一、 填空:(本题15分,每空3分。请将最终结果填在相应的横线上面。)
1. 设函数 ,
, ,且当x→0时,
,且当x→0时, 与
与 为等价无穷小,则a = 3 。
为等价无穷小,则a = 3 。
2. 设函数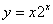 在
在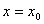 点处取得极小值,则
点处取得极小值,则
 。
。
3. 
 。
。
4. 曲线 在点(1,1,2)处的切线方程为
在点(1,1,2)处的切线方程为 。
。
5. 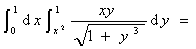
 。
。
二、选择题:(本题15分,每小题3分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)
1. 设函数 连续,则下列函数中必为偶函数的是( A )
连续,则下列函数中必为偶函数的是( A )
(A) ; (B)
; (B)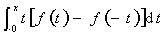 ;
;
(C) ; (D)
; (D) 。
。
2. 设函数 具有一阶导数,下述结论中正确的是( D )
具有一阶导数,下述结论中正确的是( D )
(A)若 只有一个零点,则
只有一个零点,则 必至少有两个零点;
必至少有两个零点;
(B)若 至少有一个零点,则
至少有一个零点,则 必至少有两个零点;
必至少有两个零点;
(C)若 没有零点,则
没有零点,则 至少有一个零点;
至少有一个零点;
(D)若 没有零点,则
没有零点,则 至多有一个零点。
至多有一个零点。
3. 设函数 在区间
在区间 内具有二阶导数,满足
内具有二阶导数,满足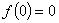 ,
, ,又
,又 ,则当
,则当 时恒有( B )
时恒有( B )
(A) ; (B)
; (B) ;
;
(C) ; (D)
; (D) 。
。
4.考虑二元函数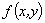 在点
在点 处的下面四条性质:
处的下面四条性质:
①连续; ②可微;
③ 与
与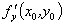 存在; ④
存在; ④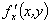 与
与 连续。
连续。
若用“P Q”表示可由性质P推出性质Q,则有( B )
Q”表示可由性质P推出性质Q,则有( B )
(A)② ③
③ ①; (B)④
①; (B)④ ②
② ①;
①;
(C)② ④
④ ①; (D)④
①; (D)④ ③
③ ②。
②。
5.设二元函数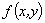 具有一阶连续偏导数,曲线L:
具有一阶连续偏导数,曲线L: 过第二象限内的点M和第四象限内的点N,Γ为L上从点M到点N的一段弧,则下列积分值为负的是( C )
过第二象限内的点M和第四象限内的点N,Γ为L上从点M到点N的一段弧,则下列积分值为负的是( C )
(A) ; (B)
; (B) ;
;
(C) ; (D)
; (D)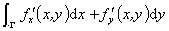 。
。
三、已知曲线 与曲线
与曲线 在点(0,0)处具有相同的切线,写出该切线方程,并求极限
在点(0,0)处具有相同的切线,写出该切线方程,并求极限 。(本题6分)
。(本题6分)
解:由已知,显然有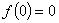 ,且在点(0,0)处
,且在点(0,0)处
 故
故
因此,所求切线方程为y = x。
 。
。
四、证明:当x > 2时, 。(本题7分)
。(本题7分)
证明:设 ,
,
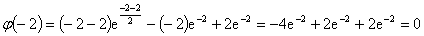 ,
,
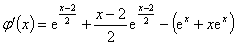 。
。
又设: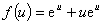 ,则
,则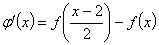 。
。
由拉格朗日中值定理知,存在 ,使
,使
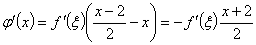 ,
,
而 ,又
,又 ,故
,故 。从而,当x > 2时,
。从而,当x > 2时,
 ,
,
即 单调减少,从而
单调减少,从而 。命题得证。
。命题得证。
五、设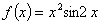 ,求
,求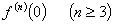 。(本题7分)
。(本题7分)
解:利用牛顿—莱布尼兹公式:
 。
。
设 ,
,
注意到: ;
;
 ,
,
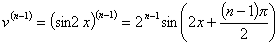 ,
,
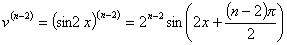 。
。
故 ,
,
于是有 。
。
六、设当 时,
时,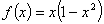 ,且
,且 ,试确定常数a的值,使
,试确定常数a的值,使 在x = 0点处可导,并求此导数。(本题7分)
在x = 0点处可导,并求此导数。(本题7分)
解:首先写出 在 x < 0附近的表达式:当
在 x < 0附近的表达式:当 时,
时, 。由
。由 知,
知,
 ,
,
故有

显然, 在点 x = 0处连续,且
在点 x = 0处连续,且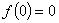 ,
,
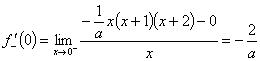 ,
,
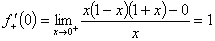 。
。
因 在x = 0点处可导的充要条件为:
在x = 0点处可导的充要条件为: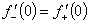 ,即
,即
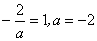 ,
,
且 。
。
七、设函数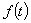 在区间
在区间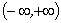 内连续,且满足
内连续,且满足 ,
,
⑴ 求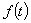 ;
;
⑵ 计算 ,其中L是从原点O到点M(1,3)的任意一条光滑弧。(本题7分)
,其中L是从原点O到点M(1,3)的任意一条光滑弧。(本题7分)
解:⑴将原等式两边对x求导,得到
 ,
,
所以 。
。
命: ,于是有
,于是有 。
。
⑵ 因为 ,
,
所以 。
。
于是可知I与积分路径无关,从而
 ,
,
命: ,当x = 0,y = 0时,t = 1;x = 1,y = 3时,t = 12。
,当x = 0,y = 0时,t = 1;x = 1,y = 3时,t = 12。
故  。
。
八、求过第一卦限中的点(a,b,c)的平面,使之与三坐标平面所围成的四面体的体积最小。(本题8分)
解:设所求平面的截距式方程为
 。
。
因平面过点(a,b,c),故有  。
。
四面体体积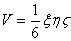 。
。
应用拉格朗日乘数法,设
 ,
,
命: 
得到  。
。
显然 ,否则
,否则 ,这与题意不符。代入上述第四个方程,得到
,这与题意不符。代入上述第四个方程,得到
 ,
,
从而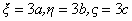 是唯一驻点,也是唯一最小值点。故所求平面为
是唯一驻点,也是唯一最小值点。故所求平面为
 。
。
九、设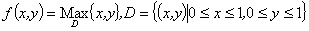 ,计算
,计算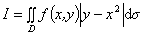 。(本题7分)
。(本题7分)
解:将区域D分成三块:

于是
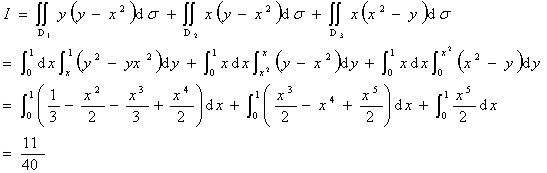
十、设函数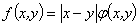 ,其中
,其中 在点(0,0)的一个邻域内连续,证明:
在点(0,0)的一个邻域内连续,证明: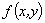 在点(0,0)处可微的充要条件是
在点(0,0)处可微的充要条件是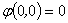 。(本题8分)
。(本题8分)
证明:充分性
已知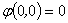 ,欲证
,欲证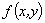 在点(0,0)处可微,只需证
在点(0,0)处可微,只需证
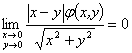 。
。
注意到:  ,
,
所以 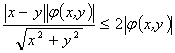 。
。
又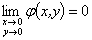 ,由夹逼定理知
,由夹逼定理知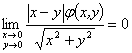 。
。
从而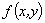 在点(0,0)处可微,并且
在点(0,0)处可微,并且 。
。
必要性
已知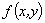 在点(0,0)处可微,故
在点(0,0)处可微,故 与
与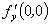 都存在。而
都存在。而
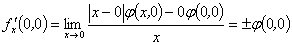 ,
,
其中当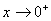 时,
时, ;当
;当 时,
时, 。由于
。由于 存在,故
存在,故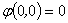 。
。
十一、计算 ,其中
,其中 为一连续函数,Σ是平面
为一连续函数,Σ是平面 在第四卦限部分的上侧。(本题7分)
在第四卦限部分的上侧。(本题7分)
解:化为第一类曲面积分求解。设Σ的单位法向量 ,则
,则

其中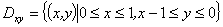 。
。
故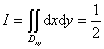 。
。
十二、设函数 在闭区间[a,b]上连续,在开区间(a,b)内可导,且有
在闭区间[a,b]上连续,在开区间(a,b)内可导,且有 ,
,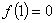 ,则至少存在一点
,则至少存在一点 ,使得
,使得 。(本题6分)
。(本题6分)
证明:由积分中值定理知,存在 ,使
,使
 。
。
又 ,故若设
,故若设 ,显然
,显然 满足罗尔定理的各个条件,从而至少存在一点
满足罗尔定理的各个条件,从而至少存在一点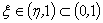 使
使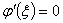 。而
。而
 ,
,
从而有  。
。
