排列组合问题的方法归纳练习
班级: 姓名:
一:特殊元素先排列:(1)特殊元素、特殊位置优先法
元素优先法:先考虑有限制条件的元素的要求,再考虑其他元素;
位置优先法:先考虑有限制条件的位置的要求,再考虑其他位置)。
1. (1995年上海高考题) 1名老师和4名获奖学生排成一排照像留念,若老师不排在两端,则共有不同的排法 种.
2.(20##年全国高考题)乒乓球队的10名队员中有3名主力队员,派5名队员参加比赛,3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有 种.
3.某班上午要上语、数、外和体育4门课,如体育不排在第一、四节;语文不排在第一、二节,则不同排课方案种数为____ _
4.某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?
5.从6名运动员中选出4人参加4×100米接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同的参赛方案
6.用0,1,2,3,4,5这六个数字,可以组成无重复数字的四位偶数_______个;
7.用1,2,3,4,5,6这6个数字组成无重复的四位数,试求满足下列条件的四位数各有多少个
(1)数字1不排在个位和千位
(2)数字1不在个位,数字6不在千位。
8.某单位准备用不同花色的装饰石材分别装饰办公楼中的办公室、走廊、大厅的地面及楼的外墙,现有编号为1到6的6种不同花色的石材可选择,其中1号石材有微量的放射性,不可用于办公室内,则不同的装饰效果有__ ___种;
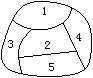 9.
9. 的一边AB上有4个点,另一边AC上有5个点,连同
的一边AB上有4个点,另一边AC上有5个点,连同 的顶点共10个点,以这些点为顶点,可以构成___ __个三角形;
的顶点共10个点,以这些点为顶点,可以构成___ __个三角形;
10.给图中区域涂色,要求相邻区域不同色,现有4种可选颜色,则不
同的着色方法有 种
二:相邻问题捆绑法(把相邻的若干个特殊元素“捆绑”为一个大元素,然后再与其余“普通元素”全排列,最后再“松绑”,将特殊元素在这些位置上全排列)。
1.把4名男生和4名女生排成一排,女生要排在一起,不同的排法种数为_____;
2. 4名男生和3名女生共坐一排,男生必须排在一起的坐法有 种?
3.有8本不同的书;其中数学书3本,外语书2本,其它学科书3本.若将这些书排成一列放在书架上,让数学书排在一起,外语书也恰好排在一起的排法共有( )种.
4.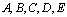 五人并排站成一排,如果
五人并排站成一排,如果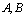 必须相邻且
必须相邻且 在
在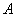 的右边,则不同的排法有( )
的右边,则不同的排法有( )
A、60种 B、48种 C、36种 D、24种
三:不相邻问题插空法:(可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端.)
1.七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是( )
A、1440种 B、3600种 C、4820种 D、4800种
3一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有 种?
1. 用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2相邻,2与4相邻,5与6相邻,而7与8不相邻。这样的八位数共有( )个.(用数字作答)
四:可重复的排列求幂法:允许重复排列问题的特点是以元素为研究对象,元素不受位置的约束,可逐一安排元素的位置,一般地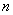 个不同元素排在
个不同元素排在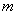 个不同位置的排列数有
个不同位置的排列数有 种方法.
种方法.
1.把6名实习生分配到7个车间实习共有多少种不同方法?
2.将5封信投入3个邮筒,不同的投法共有 种;
五:有序问题组合法
1.学号为1,2,3,4的四名学生的考试成绩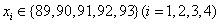 且满足
且满足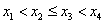 ,则这四位同学考试成绩的所有可能情况有_____种;
,则这四位同学考试成绩的所有可能情况有_____种;
2.设集合 ,对任意
,对任意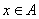 ,有
,有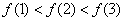 ,则映射
,则映射 的个数是_ ____;
的个数是_ ____;
3.离心率等于 (其中
(其中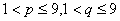 且
且 )的不同形状的的双曲线的个数为_ ____。
)的不同形状的的双曲线的个数为_ ____。
六:定序问题缩倍法:在排列问题中限制某几个元素必须保持一定的顺序,可用缩小倍数的方法.
1.A,B,C,D,E五人并排站成一排,如果 必须站在
必须站在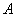 的右边(
的右边(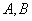 可以不相邻)那么不同的排法有( )A、24种 B、60种 C、90种 D、120种
可以不相邻)那么不同的排法有( )A、24种 B、60种 C、90种 D、120种
2.6个人排队,甲、乙、丙三人按“甲---乙---丙”顺序排的排队方法有多少种?
3.4个男生和3个女生,高矮不相等,现在将他们排成一行,要求从左到右女生从矮到高排列,有多少种排法。
4.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A、210种 B、300种 C、464种 D、600种
七:“至少”“至多”问题用间接排除法或分类法:
1.从4台甲型和5台乙型电视机中任取3台,其中至少要甲型和乙 型电视机各一台,则不同的取法共有 ( ) A、140种 B、80种 C、70种 D、35种
2.如从7名男同学和5名女同学中选出5人,至少有2名女同学当选的选法有_______种
八:多元问题分类法:元素多,取出的情况也多种,可按结果要求分成不相容的几类情况分别计数再相加。
1.某化工厂实验生产中需依次投入2种化工原料,现有5种原料可用,但甲、乙两种原料不能同时使用,且依次投料时,若使用甲原料,则甲必须先投放. 那么不同的实验方案共有_______种;
2.某公司新招聘进8名员工,平均分给下属的甲、乙两个部门.其中两名英语翻译人员不能同给一个部门;另三名电脑编程人员也不能同给一个部门,则不同的分配方案有_____种;
九:阁板法,名额分配或相同物品的分配问题,适宜采阁板用法,(每组至少一份),(每组至少一份,分成n份,需要n-1个隔板,当不是每组至少一份时,先转化为每组至少一份后再做)
1. 某校准备组建一个由12人组成篮球队,这12个人由8个班的学生组成,每班至少一人,名额分配方案共 种 。
2.10个三好学生名额分到7个班级,每个班级至少一个名额,有多少种不同分配方案?
3.10个相同的球各分给3个人,每人至少一个,有多少种分发?每人至少两个呢?
4.有20个不加区别的小球放入编号为1,2,3的三个盒子里,要求每个盒子内的球数不少编号数,问有多少种不同的方法?
十.(不同物品)分组问题:要注意区分是平均分组还是非平均分组,平均分成n组问题别忘除以n!。
1.本不同的书平均分成三堆,有多少种不同的方法?
2.把6个不同苹果平均分成三堆,一共有 种分法.
3.把6个不同苹果平均分成3份给3个小朋友,一共有 种分法.
4.把6个不同的苹果分成4堆,一共有 种分法.
5.把6个不同苹果分给4个小朋友,每个小朋友至少1个,一共有 种分法.
6.6本书分三份,2份1本,1份4本,则有不同分法?
7.4名优秀学生全部保送到3所学校去,每所学校至少去一名,则不同的保送方案有多少种?
8.5本不同的书,全部分给4个学生,每个学生至少一本,不同的分法种数为( )
A、480种 B、240种 C、120种 D、96种
9.某年级6个班的数学课,分配给甲乙丙三名数学教师任教,每人教两个班,则分派方法的种数。
10.12名同学分别到三个不同的路口进行流量的调查,若每个路口4人,则不同的分配方案有( )
A、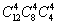 种 B、
种 B、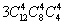 种 C、
种 C、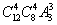 种 D、
种 D、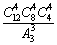 种
种
11.有甲乙丙三项任务,甲需2人承担,乙丙各需一人承担,从10人中选出4人承担这三项任务,不同的选法种数是( )
A、1260种 B、2025种 C、2520种 D、5040种
12.如4名医生和6名护士组成一个医疗小组,若把他们分配到4所学校去为学生体检,每所学校需要一名医生和至少一名护士的不同选派方法有_______种;
十一:选排问题先取后排:从几类元素中取出符合题意的几个元素,再安排到一定的位置上,可用先取后排法.
1.如某种产品有4只次品和6只正品,每只产品均不相同且可区分,今每次取出一只测试,直到4只次品全测出为止,则最后一只次品恰好在第五次测试时,被发现的不同情况种数是_ _。
2.四个不同球放入编号为1,2,3,4的四个盒中,则恰有一个空盒的放法有多少种?
3.9名乒乓球运动员,其中男5名,女4名,现在要进行混合双打训练,有多少种不同的分组方法?
十二:标号排位问题分步法:把元素排到指定位置上,可先把某个元素按规定排入,第二步再排另一个元素,如此继续下去,依次即可完成.
1.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有( )
A、6种 B、9种 C、11种 D、23种
2.同室4人各写1张贺年卡,然后每人从中拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有 种;
3.设有编号为1、2、3、4、5的五个茶杯和编号为1、2、3、4、5的5个杯盖,将五个杯盖盖在五个茶杯上,至少有两个杯盖和茶杯的编号相同的盖法有______ ___种
4.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的盒子现将这5个球投入5个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?
十三:多排问题单排法:把元素排成几排的问题可归结为一排考虑,再分段处理。
1.如若2n个学生排成一排的排法数为x,这2 n个学生排成前后两排,每排各n个学生的排法数为y,则x,y的大小关系为_____;
2. 6个不同的元素排成前后两排,每排3个元素,那么不同的排法种数是( )
A、36种 B、120种 C、720种 D、1440种
3.8个不同的元素排成前后两排,每排4个元素,其中某2个元素要排在前排,某1个元素排在后排,有多少种不同排法?
十四:圆排问题单排法:把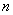 个不同元素放在圆周
个不同元素放在圆周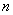 个无编号位置上的排列,顺序(例如按顺时钟)不同的排法才算不同的排列,而顺序相同(即旋转一下就可以重合)的排法认为是相同的,它与普通排列的区别在于只计顺序而首位、末位之分,下列
个无编号位置上的排列,顺序(例如按顺时钟)不同的排法才算不同的排列,而顺序相同(即旋转一下就可以重合)的排法认为是相同的,它与普通排列的区别在于只计顺序而首位、末位之分,下列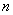 个普通排列:
个普通排列:
 在圆排列中只算一种,因为旋转后可以重合,故认
在圆排列中只算一种,因为旋转后可以重合,故认
为相同,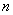 个元素的圆排列数有
个元素的圆排列数有 种.因此可将某个元素固定展成单排,其它的
种.因此可将某个元素固定展成单排,其它的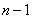 元素全排列.
元素全排列.
1.有5个人站成一圈,一共有多少种站法?
1.有5对姐妹站成一圈,要求每对姐妹相邻,有多少种不同站法?
十五:排除法,部分合条件问题排除法:在选取的总数中,只有一部分合条件,可以从总数中减去不符合条件数,即为所求.
1.以正方体的顶点为顶点的四面体共有( )
A、70种 B、64种 C、58种 D、52种
2. 有五张卡片,它的正反面分别写0与1,2与3,4与5,6与7,8与9,将它们任意三张并排放在一起组成三位数,共可组成多少个不同的三维书?
3.如在平面直角坐标系中,由六个点(0,0),(1,2),(2,4),(6,3),(-1,-2),(-2,-1)可以确定三角形的个数为_____。
十六:已排好元素中新增元素增位排列法
1.在一个含有8个节目的节目单中,临时插入两个歌唱节目,且保持原节目顺序,有多少中插入方法?
2.某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目。如果将这两个节目插入原节目单中,那么不同的插法种数为___ __。
3.如(1)书架上有3本不同的书,如果保持这些书的相对顺序不便,再放上2本不同的书,有 种不同的放法;
第二篇:排列组合归纳总结
排列、组合及二项式定理
一、计数
yi 分类加法计数原理和分步乘法计数原理 →
1.分类加法计数原理定义
完成一件事,可以有n类办法,在第一类办法中有m1种方法,在第二类办法中有m2种方法,……,在第n类办法中有mn种不同的方法,那么,完成这件事情共有N=m1+ m2+…+mn种不同的方法.
2.分步乘法计数原理定义
完成一件事情需要经过n个步骤,缺一不可,做第一步有m1种方法,做第二步有m2种方法,……,做第n步有mn种方法,那么完成这件事共有N=m1 m2…mn种不同的方法.
3.分类加法计数原理与分步乘法计数原理区别与联系
联系;都涉及完成一件事情的不同方法的种数.
区别:分类加法计数原理与分类有关,各种方法相互独立,用其中的任一种方法都可以完成这件事;分步乘法计数原理与分步有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.
4. 分类分步标准
分类就是一步到位,(1)类与类之间要互斥;(2)总数完整。
分步是局部到位,(1)按事件发生的连贯过程进行分步;(2)步与步之间相互独立,互不干扰;(3)保证连续性。
→ 排列与组合
1.排列
(1)排列定义:从n个不同元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
(2)排列数公式:A=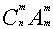 =n(n-1)(n-2)…(n-m+1)或写成A=.特殊: An n=n!=n(n-1)!
=n(n-1)(n-2)…(n-m+1)或写成A=.特殊: An n=n!=n(n-1)!
(3)特征:有序且不重复
2.组合
(1)组合定义:从n个不同元素中,任取m(m≤n)个元素组成一组,叫做从n个不同元素中取出m个元素的一个组合.
(2)组合数公式:C= =或写成C=.
=或写成C=.
(3)组合数的性质
①C=C;
②C=C+C.
(4)特征:有序且不重复
3.排列与组合的区别与联系:
区别:排列有序,组合无序
联系:排列可视为先组合后全排
4.基本原则:(1)先特殊后一般;(2)先选后排;(3)先分类后分步。
→排列组合的应用(常用方法:直接法,间接法)
1.抽取问题:
(1)关键:特殊优先;
(2)题型:① 把n个相同的小球,一次性的放入到m个不同的盒子中(n≤m),每个盒子至少1个,有多少种不同的方法?Cmn
②把n个相同的小球,依次性的放入到m个不同的盒子中(n≤m),每个盒子至少1个,有多少种不同的方法?Amn
③把n个相同的小球,放入到m个不同的盒子中(n≤m),每个盒子放球数目不限,有多少种不同的方法?mn
④把n个不同的小球,放入到m个不同的盒子中(n≤m),每个盒子至少1个,有多少种不同的方法?Amn
⑤把n个相同的小球,依次性的放入到m个不同的盒子中(n≥m),每个盒子至多1个,有多少种不同的方法?Cn-1m-1 隔板法
2.排序问题:特殊优先
(1)排队问题:
① 对n个元素做不重复排序Ann;
② 对n个元素进行(其中有m个元素的位置固定)排列 ;如果对n个元素进行(其中有m个元素的位置固定,k个元素的位置固定)排列
;如果对n个元素进行(其中有m个元素的位置固定,k个元素的位置固定)排列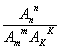 ;
;
③ 相邻问题—捆绑法(注意松绑);
④不相邻问题:(a)一方不相邻—先排没要求的元素,再把不相邻的元素插入空位; (b)互不相邻先排少的在插入多的;
(2)数字问题;
①各位相加为奇数的-----奇数的个数是奇数;
②各位相加为偶数的-----奇数的个数是偶数;
③组成n为偶数(奇数)的数----特殊优先法;
④能被n整除的数-----特殊优先法;
⑤比某数大的数,比某数小的数或某数的位置----从大于(小于)开始排,再排等于;
(3)着色问题:
①区域优先-----颜色就是分类点;
②颜色优先-----区域就是分类点.
(4)几何问题:①点、 线、 面的关系一般均为组合问题;

 ②图中有多少个矩形 C
6
2 C
4
2;从A到B
②图中有多少个矩形 C
6
2 C
4
2;从A到B
的最短距离 C83
(5)分组、分配问题:
①非均分不编号;n个不同元素分成m组,每组元素数目均不相等,且不考虑各组间的顺序,不考虑是否分尽---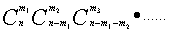
②非均分编号;n个不同元素分成m组,每组组元素数目均不相等,且考虑各组间的顺序,不考虑是否分尽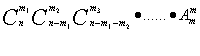
③均分不编号;n个不同元素分成m组,其中有k组元素数目均相等,且不考虑各组间的顺序,不考虑是否分尽
④均分编号;n个不同元素分成m组,其中有k组元素数目均相等,且考虑各组间的顺序,不考虑是否分尽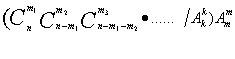
二、二项式定理
1.定理:(a+b)n=Canb0+Can-1b+Can-2b2+…+Can-rbr+…+Ca0bn(r=0,1,2,…,n).
2.二项展开式的通项
Tr+1=Can-rbr,r=0,1,2,…,n,其中C叫做二项式系数.
3.二项式系数的性质
①对称性:与首末两端“等距离”两项的二项式系数相等,
即C=C,C=C,…,C=C,….
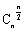 ②最大值:当n为偶数时,中间的一项的二项式系数
②最大值:当n为偶数时,中间的一项的二项式系数
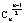
 取得最大值;当n为奇数时,中间的两项的二项式系数
取得最大值;当n为奇数时,中间的两项的二项式系数
, 相等,且同时取得最大值.
③各二项式系数的和
a.C+C+C+…+C+…+C=2n;
b.C+C+…+C+…=C+C+…+C+…=·2n=2n-1.
→二项式定理的应用:
1.求通项; 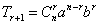
2.含xr的项:① 项的系数;②二项式系数。
3.常数项(含xr的项中r=0)整数项(含xr的项中r∈N)有理项(含xr的项中r∈Z)无理项(含xr的项中r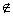 Z)
Z)
4.项的系数和:
(1)已知多项式f(x)=(a+bx)n(a,b>0)=a0 +a1x+a2x2+…+anxn:
①a0 =f(0)
②a0 +a1+a2+…+an = f(1)= (a+b)n;
③|a0 |+|a1 |+|a2 |+…+|an |= f(1)= (a+b)n;
④a0 +a2+a4+…=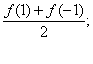
⑤a1 +a3+a5+…=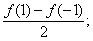
⑥(a0 +a2+a4+…)2-( a1 +a3+a5+…)2=f(1)f(-1)。
(2)已知多项式f(x)=(a-bx)n(a,b>0)=a0 +a1x+a2x2+…+anxn:
①a0 =f(0)
②a0 +a1+a2+…+an = f(1)= (a-b)n;
③|a0 |+|a1 |+|a2 |+…+|an |= f(-1)= (a+b)n;
④a0 +a2+a4+…=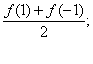
⑤a1 +a3+a5+…=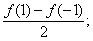
⑥(a0 +a2+a4+…)2-( a1 +a3+a5+…)2=f(1)f(-1)。
(3) 已知多项式f(x)=(ax-b)n(a,b>0)=a0 +a1x+a2x2+…+anxn:
令g(x)=(-1)n(b-ax)n
①a0 =f(0)
②a0 +a1+a2+…+an = f(1)= (a-b)n;
③|a0 |+|a1 |+|a2 |+…+|an |=|(-1)n|g(-1)
④a0 +a2+a4+…=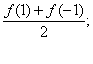
⑤a1 +a3+a5+…=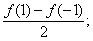
⑥(a0 +a2+a4+…)2-( a1 +a3+a5+…)2=f(1)f(-1)。
(4) 已知多项式f(x)=(-ax-b)n(a,b>0)=a0 +a1x+a2x2+…+anxn:
令g(x)=(-1)n(ax+b)n
①a0 =f(0)
②a0 +a1+a2+…+an = f(1)= (a-b)n;
③|a0 |+|a1 |+|a2 |+…+|an |=|(-1)n|g(1)
④a0 +a2+a4+…=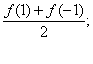
⑤a1 +a3+a5+…=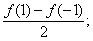
⑥(a0 +a2+a4+…)2-( a1 +a3+a5+…)2=f(1)f(-1)。
5.最值问题:
① 二项式系数最大:(a)当n为偶数时,二项式系数中, 最大;(b)当n为奇数时,二项式系数中,
最大;(b)当n为奇数时,二项式系数中,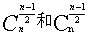 最大
最大
②项的是系数最大:

 表示第r+1项的系数
表示第r+1项的系数
(a) 个项都为正数时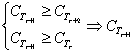 最大;
最大;
(b) 一项为正一项为负时 最大
最大
