★二次函数知识点汇总★
1.定义:一般地,如果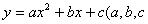 是常数,
是常数,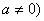 ,那么
,那么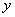 叫做
叫做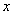 的二次函数.
的二次函数.
2.二次函数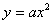 的性质
的性质
(1)抛物线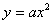
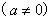 的顶点是坐标原点,对称轴是
的顶点是坐标原点,对称轴是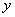 轴.(2)函数
轴.(2)函数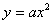 的图像与
的图像与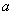 的符号关系.
的符号关系.
①当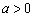 时
时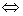 抛物线开口向上
抛物线开口向上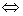 顶点为其最低点;②当
顶点为其最低点;②当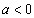 时
时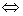 抛物线开口向下
抛物线开口向下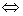 顶点为其最高点
顶点为其最高点
3.二次函数  的图像是对称轴平行于(包括重合)
的图像是对称轴平行于(包括重合)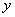 轴的抛物线.
轴的抛物线.
4.二次函数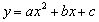 用配方法可化成:
用配方法可化成: 的形式,其中
的形式,其中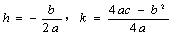 .
.
5.二次函数由特殊到一般,可分为以下几种形式:
①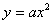 ;②
;②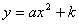 ;③
;③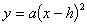 ;④
;④ ;⑤
;⑤ .
.
6.抛物线的三要素:开口方向、对称轴、顶点.
①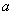 决定抛物线的开口方向:
决定抛物线的开口方向:
当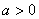 时,开口向上;当
时,开口向上;当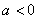 时,开口向下;
时,开口向下; 相等,抛物线的开口大小、形状相同.
相等,抛物线的开口大小、形状相同.
②平行于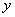 轴(或重合)的直线记作
轴(或重合)的直线记作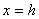 .特别地,
.特别地,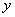 轴记作直线
轴记作直线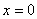 .
.
7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数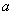 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
8.求抛物线的顶点、对称轴的方法
(1)公式法: ,∴顶点是
,∴顶点是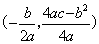 ,对称轴是直线
,对称轴是直线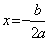 .
.
(2)配方法:运用配方法将抛物线的解析式化为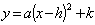 的形式,得到顶点为(
的形式,得到顶点为(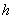 ,
,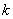 ),对称轴是
),对称轴是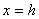 .
.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.
★用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失★
9.抛物线 中,
中,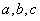 的作用
的作用
(1)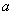 决定开口方向及开口大小,这与
决定开口方向及开口大小,这与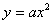 中的
中的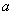 完全一样.
完全一样.
(2)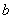 和
和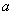 共同决定抛物线对称轴的位置.由于抛物线
共同决定抛物线对称轴的位置.由于抛物线 的对称轴是直线
的对称轴是直线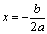 ,故:
,故:
① 时,对称轴为
时,对称轴为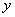 轴;②
轴;② (即
(即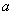 、
、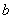 同号)时,对称轴在
同号)时,对称轴在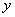 轴左侧;
轴左侧;
③ (即
(即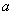 、
、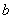 异号)时,对称轴在
异号)时,对称轴在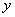 轴右侧.
轴右侧.
(3)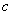 的大小决定抛物线
的大小决定抛物线 与
与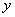 轴交点的位置.
轴交点的位置.
当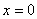 时,
时,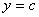 ,∴抛物线
,∴抛物线 与
与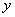 轴有且只有一个交点(0,
轴有且只有一个交点(0,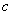 ):
):
①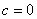 ,抛物线经过原点; ②
,抛物线经过原点; ②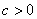 ,与
,与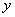 轴交于正半轴;③
轴交于正半轴;③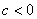 ,与
,与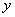 轴交于负半轴.
轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在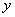 轴右侧,则
轴右侧,则 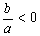 .
.
10.几种特殊的二次函数的图像特征如下:

11.用待定系数法求二次函数的解析式
(1)一般式: .已知图像上三点或三对
.已知图像上三点或三对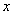 、
、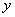 的值,通常选择一般式.
的值,通常选择一般式.
(2)顶点式: .已知图像的顶点或对称轴,通常选择顶点式.
.已知图像的顶点或对称轴,通常选择顶点式.
(3)交点式:已知图像与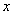 轴的交点坐标
轴的交点坐标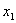 、
、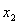 ,通常选用交点式:
,通常选用交点式: .
.
12.直线与抛物线的交点
(1)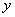 轴与抛物线
轴与抛物线 得交点为(
得交点为(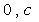 )
)
(2)与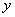 轴平行的直线
轴平行的直线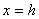 与抛物线
与抛物线 有且只有一个交点(
有且只有一个交点(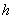 ,
,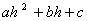 ).
).
(3)抛物线与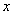 轴的交点
轴的交点
二次函数 的图像与
的图像与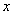 轴的两个交点的横坐标
轴的两个交点的横坐标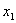 、
、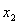 ,是对应一元二次方程
,是对应一元二次方程
 的两个实数根.抛物线与
的两个实数根.抛物线与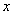 轴的交点情况可以由对应的一元二次方程的根的判别式判定:
轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点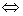

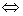 抛物线与
抛物线与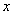 轴相交;
轴相交;
②有一个交点(顶点在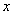 轴上)
轴上)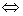
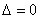
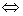 抛物线与
抛物线与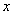 轴相切;
轴相切;
③没有交点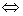
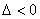
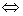 抛物线与
抛物线与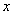 轴相离.
轴相离.
(4)平行于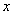 轴的直线与抛物线的交点
轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为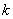 ,则横坐标是
,则横坐标是 的两个实数根.
的两个实数根.
(5)一次函数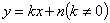 的图像
的图像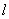 与二次函数
与二次函数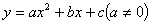 的图像
的图像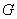 的交点,由方程组
的交点,由方程组
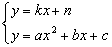 的解的数目来确定:
的解的数目来确定:
①方程组有两组不同的解时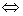
 与
与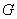 有两个交点;
有两个交点;
②方程组只有一组解时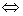
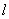 与
与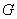 只有一个交点;③方程组无解时
只有一个交点;③方程组无解时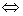
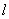 与
与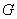 没有交点.
没有交点.
(6)抛物线与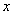 轴两交点之间的距离:若抛物线
轴两交点之间的距离:若抛物线 与
与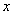 轴两交点为
轴两交点为 ,由于
,由于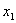 、
、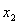 是方程
是方程 的两个根,故
的两个根,故 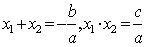
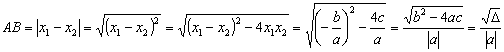
13.二次函数与一元二次方程的关系:
(1)一元二次方程 就是二次函数
就是二次函数 当函数y的值为0时的情况.
当函数y的值为0时的情况.
(2)二次函数 的图象与
的图象与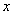 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数
轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数 的图象与
的图象与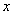 轴有交点时,交点的横坐标就是当
轴有交点时,交点的横坐标就是当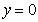 时自变量
时自变量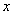 的值,即一元二次方程
的值,即一元二次方程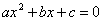 的根.
的根.
(3)当二次函数 的图象与
的图象与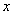 轴有两个交点时,则一元二次方程
轴有两个交点时,则一元二次方程 有两个不相等的实数根;当二次函数
有两个不相等的实数根;当二次函数 的图象与
的图象与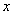 轴有一个交点时,则一元二次方程
轴有一个交点时,则一元二次方程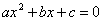 有两个相等的实数根;当二次函数
有两个相等的实数根;当二次函数 的图象与
的图象与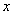 轴没有交点时,则一元二次方程
轴没有交点时,则一元二次方程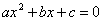 没有实数根
没有实数根
14.二次函数的应用:
(1)二次函数常用来解决最优化问题,这类问题实际上就是求函数的最大(小)值;
(2)二次函数的应用包括以下方面:分析和表示不同背景下实际问题中变量之间的二次函数关系;
运用二次函数的知识解决实际问题中的最大(小)值.
15.解决实际问题时的基本思路:(1)理解问题;(2)分析问题中的变量和常量;(3)用函数表达式表示出它们之间的关系;(4)利用二次函数的有关性质进行求解;(5)检验结果的合理性,对问题加以拓展等.
第二篇:初三数学二次函数知识点总结
一、二次函数图象的平移
1. 平移步骤:
方法一:⑴ 将抛物线解析式转化成顶点式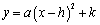 ,确定其顶点坐标
,确定其顶点坐标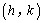 ;
;
⑵ 保持抛物线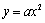 的形状不变,将其顶点平移到
的形状不变,将其顶点平移到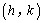 处,具体平移方法如下:
处,具体平移方法如下:

2. 平移规律
在原有函数的基础上“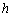 值正右移,负左移;
值正右移,负左移; 值正上移,负下移”.
值正上移,负下移”.
概括成八个字“左加右减,上加下减”.
方法二:
⑴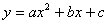 沿
沿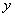 轴平移:向上(下)平移
轴平移:向上(下)平移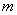 个单位,
个单位,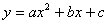 变成
变成
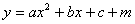 (或
(或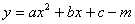 )
)
⑵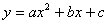 沿轴平移:向左(右)平移
沿轴平移:向左(右)平移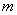 个单位,
个单位,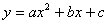 变成
变成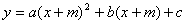 (或
(或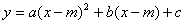 )
)
二、二次函数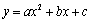 的性质
的性质
1. 当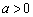 时,抛物线开口向上,对称轴为
时,抛物线开口向上,对称轴为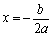 ,顶点坐标为
,顶点坐标为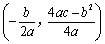 .
.
当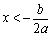 时,
时,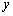 随
随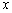 的增大而减小;当
的增大而减小;当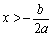 时,
时,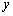 随
随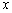 的增大而增大;当
的增大而增大;当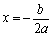 时,
时,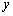 有最小值
有最小值 .
.
2. 当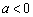 时,抛物线开口向下,对称轴为
时,抛物线开口向下,对称轴为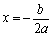 ,顶点坐标为
,顶点坐标为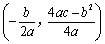 .当
.当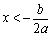 时,
时,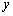 随
随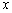 的增大而增大;当
的增大而增大;当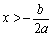 时,
时,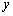 随
随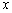 的增大而减小;当
的增大而减小;当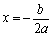 时,
时,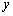 有最大值
有最大值 .
.
三、二次函数解析式的表示方法
1. 一般式: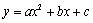 (
( ,
,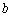 ,
,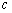 为常数,
为常数,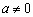 );
);
2. 顶点式: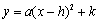 (
( ,
,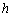 ,
, 为常数,
为常数,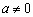 );
);
3. 两根式: (
(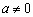 ,
, ,
,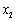 是抛物线与
是抛物线与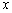 轴两交点的横坐标).
轴两交点的横坐标).
四、二次函数的图象与各项系数之间的关系
1. 二次项系数
二次函数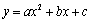 中,
中, 作为二次项系数,显然
作为二次项系数,显然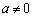 .
.
⑴ 当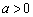 时,抛物线开口向上,
时,抛物线开口向上, 的值越大,开口越小,反之
的值越大,开口越小,反之 的值越小,开口越大;
的值越小,开口越大;
⑵ 当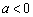 时,抛物线开口向下,
时,抛物线开口向下, 的值越小,开口越小,反之
的值越小,开口越小,反之 的值越大,开口越大.
的值越大,开口越大.
总结起来, 决定了抛物线开口的大小和方向,
决定了抛物线开口的大小和方向, 的正负决定开口方向,
的正负决定开口方向,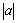 的大小决定开口的大小.
的大小决定开口的大小.
2. 一次项系数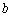
在二次项系数 确定的前提下,
确定的前提下,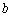 决定了抛物线的对称轴.
决定了抛物线的对称轴.
⑴ 在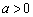 的前提下,
的前提下,
当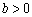 时,
时, ,即抛物线的对称轴在
,即抛物线的对称轴在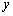 轴左侧;
轴左侧;
当 时,
时, ,即抛物线的对称轴就是
,即抛物线的对称轴就是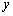 轴;
轴;
当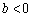 时,
时,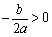 ,即抛物线对称轴在
,即抛物线对称轴在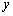 轴的右侧.
轴的右侧.
⑵ 在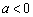 的前提下,结论刚好与上述相反,即
的前提下,结论刚好与上述相反,即
当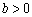 时,
时,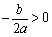 ,即抛物线的对称轴在
,即抛物线的对称轴在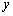 轴右侧;
轴右侧;
当 时,
时, ,即抛物线的对称轴就是
,即抛物线的对称轴就是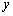 轴;
轴;
当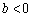 时,
时, ,即抛物线对称轴在
,即抛物线对称轴在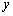 轴的左侧.
轴的左侧.
总结起来,在 确定的前提下,
确定的前提下,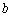 决定了抛物线对称轴的位置.
决定了抛物线对称轴的位置.
 的符号的判定:对称轴
的符号的判定:对称轴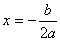 在
在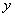 轴左边则
轴左边则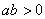 ,在
,在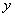 轴的右侧则
轴的右侧则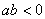 ,概括的说就是“左同右异”
,概括的说就是“左同右异”
五、二次函数图象的对称
二次函数图象的对称一般有三种情况,可以用一般式或顶点式表达
1. 关于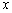 轴对称
轴对称
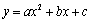 关于
关于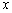 轴对称后,得到的解析式是
轴对称后,得到的解析式是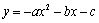 ;
;
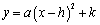 关于
关于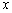 轴对称后,得到的解析式是
轴对称后,得到的解析式是 ;
;
2. 关于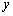 轴对称
轴对称
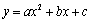 关于
关于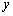 轴对称后,得到的解析式是
轴对称后,得到的解析式是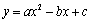 ;
;
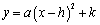 关于
关于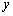 轴对称后,得到的解析式是
轴对称后,得到的解析式是 ;
;
3. 关于原点对称
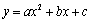 关于原点对称后,得到的解析式是
关于原点对称后,得到的解析式是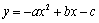 ;
;
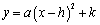 关于原点对称后,得到的解析式是
关于原点对称后,得到的解析式是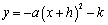 ;
;
1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:
已知以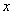 为自变量的二次函数
为自变量的二次函数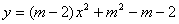 的图像经过原点, 则
的图像经过原点, 则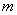 的值是
的值是
2. 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如:
已知一条抛物线经过(0,3),(4,6)两点,对称轴为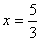 ,求这条抛物线的解析式。
,求这条抛物线的解析式。
3. 考查用配方法求抛物线的顶点坐标、对称轴、二次函数的极值,有关试题为解答题,如:
已知抛物线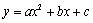 (a≠0)与x轴的两个交点的横坐标是-1、3,与y轴交点的纵坐标是-
(a≠0)与x轴的两个交点的横坐标是-1、3,与y轴交点的纵坐标是-
(1)确定抛物线的解析式;(2)用配方法确定抛物线的开口方向、对称轴和顶点坐标.
5.考查代数与几何的综合能力,常见的作为专项压轴题。
【例题经典】
例1 (1)二次函数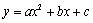 的图像如图1,则点
的图像如图1,则点 在( )
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(2)已知二次函数y=ax2+bx+c(a≠0)的图象如图2所示,则下列结论:①a、b同号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=-2时,x的值只能取0.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
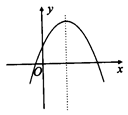

(1) (2)
例2.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,O)、(x1,0),且1<x1<2,与y轴的正半轴的交点在点(O,2)的下方.下列结论:①a<b<0;②2a+c>O;③4a+c<O;④2a-b+1>O,其中正确结论的个数为( )
A 1个 B. 2个 C. 3个 D.4个
例3、 “已知函数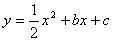 的图象经过点A(c,-2),
的图象经过点A(c,-2),
求证:这个二次函数图象的对称轴是x=3。”题目中的矩形框部分是一段被墨水污染了无法辨认的文字。
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数图象;若不能,请说明理由。
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整。
二次函数对应练习试题
一、选择题
1. 二次函数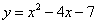 的顶点坐标是( )
的顶点坐标是( )
A.(2,-11) B.(-2,7) C.(2,11) D. (2,-3)
2. 把抛物线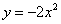 向上平移1个单位,得到的抛物线是( )
向上平移1个单位,得到的抛物线是( )
A. 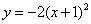 B.
B.  C.
C.  D.
D. 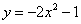
3.已知抛物线过点A(2,0),B(-1,0),与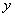 轴交于点C,且OC=2.则这条抛物线的解析式为
轴交于点C,且OC=2.则这条抛物线的解析式为
A. 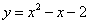 B.
B. 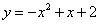
C. 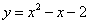 或
或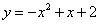 D.
D. 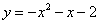 或
或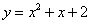
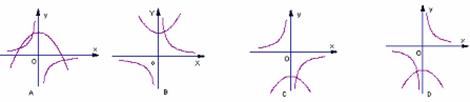 4函数
4函数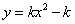 和
和 在同一直角坐标系中图象可能是图中的( )
在同一直角坐标系中图象可能是图中的( )
 5.已知二次函数
5.已知二次函数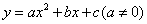 的图象如图所示,则下列结论: ①a,b同号;②当
的图象如图所示,则下列结论: ①a,b同号;②当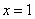 和
和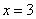 时,函数值相等;③
时,函数值相等;③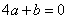 ④当
④当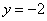 时,
时, 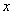 的值只能取0.其中正确的个数是( )
的值只能取0.其中正确的个数是( )
A.1个 B.2个 C. 3个 D. 4个
6. 已知二次函数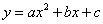 的图象如图所示,则点
的图象如图所示,则点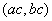 在( )
在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
二、填空题
7.已知抛物线y=-2(x+3)²+5,如果y随x的增大而减小,那么x的取值范围是_______.
8.一个函数具有下列性质:①图象过点(-1,2),②当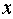 <0时,函数值
<0时,函数值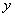 随自变量
随自变量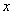 的增大而增大;满足上述两条性质的函数的解析式是 (只写一个即可)。
的增大而增大;满足上述两条性质的函数的解析式是 (只写一个即可)。
9. 二次函数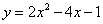 的图象是由
的图象是由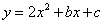 的图象向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
的图象向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
10.如图,抛物线 经过直线
经过直线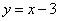 与坐标轴的两个交点A、B,此抛物线与
与坐标轴的两个交点A、B,此抛物线与 轴的另一个交点为C,抛物线顶点为D.
轴的另一个交点为C,抛物线顶点为D.
(1)求此抛物线的解析式;
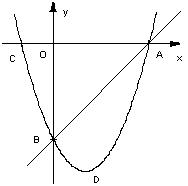 (2)点P为抛物线上的一个动点,求使
(2)点P为抛物线上的一个动点,求使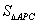 :
: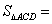 5 :4的点P的坐标。
5 :4的点P的坐标。
