14.2.2 完全平方公式
一、学习目标
1、会判断完全平方式。
2、能直接利用完全平方因式分解。
3、掌握利用完全平方公式因式分解的步骤。
二、自主预习
因式分解:2a2b-4ab2=__________,-3a3b+12ab3=__________.
1、填空:(a+b)2=__________,(a-b)2=__________.
2、根据上面的式子填空:
a2+2ab+b2=__________,a2-2ab+b2=__________.
3、形如a2+__________+b2与a2-__________+b2的式子称为完全平方式.
完全平方式:a2±2ab+b2=(a±b)2
语言叙述:两个数的__________加上(减去)这两个数__________,等于这两个数的和(差)的平方。
三、合作探究
1、判断下列多项式是否为完全平方式,如果是运用完全平方公式将其因式分解。
①b2+b+1 ②a2-ab+b2 ③1+4a2 ④a2-a+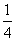
2、分解因式:①x2+12x+36 ②—2xy—x2—y2 ③ax2+2a2x+a3
3、已知 ,求:⑴
,求:⑴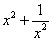 的值;⑵
的值;⑵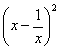 的值.
的值.
4、已知 ,求ab的值.
,求ab的值.
四、当堂评价
1、分解因式:
⑴a2+ab+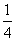 b2 ⑵-2x3y+4x2y-2xy
b2 ⑵-2x3y+4x2y-2xy
⑶(a-b) 2-6(b-a)+9 ⑷(x2-2x)2+2(x2-2x)+1
2、因式分解:
⑴(a2-4a)2+8(a2-4a)+16 ⑵2x2-12x+18
⑶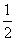 x2+xy+
x2+xy+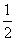 y2 ⑷abx2+2abxy+aby2
y2 ⑷abx2+2abxy+aby2
五、拓展提升
1、把下列各式分解因式:
⑴4-12(x-y)+9(x-y) 2 ⑵(x2y2+1)2-4x2y2
2、若M=(x2+y2)2(x2-y2)2,N=(x4+x2y2+y4)(x4-x2y2+y4),且xy≠0,请比较M、N的大小.
3、试证明:不论x、y取何值,x2-4y+y2-6y+13的值不小于0.
六、课后检测
1、因式分解:
⑴x2+x+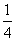 ⑵x2-4(x-1)
⑵x2-4(x-1)
⑶25x2+20xy+4y2 ⑷a3-10a2+25a
⑸(x2+4y2)2-16x2y2 ⑹(x2+3x)2-(x-1)2
⑺(a+b)2-6(a+b)+9 ⑻(x+y)2-6x2+6y2+9(x-y)2
2、用简便方法计算:
⑴212-42+1 ⑵662-6600+502
3、已知a、b、c是△ABC的三边,且满足关系式a2+c2=2ab+2bc-2b2,试说明△ABC是等边三角形.
七、课堂小结:学生总结,这节课学到了什么?
八、教学反思:
第二篇:完全平方公式
完全平方公式
一、学习目标:
1.理解两数和的平方的公式,掌握公式的结构特征,并熟练地应用公式进行计算.
2.经历探索两数和的平方公式的过程,进一步发展学生的符号感和推理能力.
3.培养学生探索能力和概括能力,体会数形结合的思想.
二、重点:对两数和的平方公式的理解,熟练完全平方公式运用进行简单的计算.
难点:对公式的理解, 包括它的推导过程,结构特点,语言表述及其几何解释.
三、自主学习:
(1)两数和乘以这两数的差的公式是什么?
(2)口述多项式乘以多项式法则.
(3)计算 (2x-1)(3x-4) (5x+3)(5x-3)
四、互动学案:
1、计算下列多项式的积,你能发现什么规律?
① 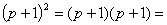
 ②
②
③ =
=
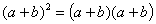 ④ =
④ =
⑤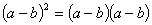 =
=
⑥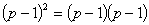 =
=
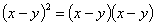 ⑦ =
⑦ =
2、(a+b)2=a2+b2对吗?为什么?
3.仿照公式计算.
(1)(x+y)2 (2)(x - y)2
例1.计算:⑴(2a+3b)2; ⑵(2)(2a+ )2 ⑶
)2 ⑶
例2.计算:(1)(a-b)2; (2)(2x-3y)2
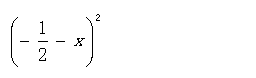
(3) (4)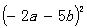
五、自主测评:
1.a2+b2 =(a+b)2 - 2.a2+b2 =(a-b)2 +
3.若x+y=5,xy=3,则x2+y2 =
4.计算:(x+5)2-(x-2)(x-3)=
5.代数式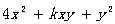 是关于
是关于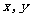 的一个完全平方式,则
的一个完全平方式,则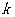 =
=
六、计算:⑴ ⑵
⑵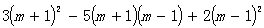
3、已知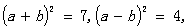 求
求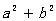 和
和 的值。
的值。
4、已知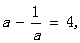 求
求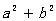 的值.
的值.
5、若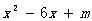 是完全平方式,则m=
是完全平方式,则m=
6、已知 ,则
,则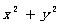 =
=
七、教学反思
完全平方公式
一、学习目标:
1.理解两数和的平方的公式,掌握公式的结构特征,并熟练地应用公式进行计算.
2.经历探索两数和的平方公式的过程,进一步发展学生的符号感和推理能力.
3.培养学生探索能力和概括能力,体会数形结合的思想.
二、重点:对两数和的平方公式的理解,熟练完全平方公式运用进行简单的计算.
难点:对公式的理解, 包括它的推导过程,结构特点,语言表述及其几何解释.
三、自主测评:
1、判断正误:
(1)(b-4a)2=b2-16a2.( ) (2)(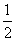 a+b)2=
a+b)2=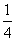 a2+ab+b2.( )
a2+ab+b2.( )
(3)(4m-n)2=16m2-4mn+n2.( ) (4)(-a-b)2=a2-2ab+b2.( )
2、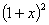 (2)
(2)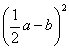
四、互动学案:
1、运用完全平方公式计算:
(1)1022 (2)1992 (3)(x+2)2-(x-2)2
2、运用乘法公式计算:
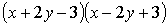
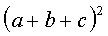 (1) (2)
(1) (2)
3、总结添括号的法则:
五、自主测评:
1、利用完全平方公式进行简便计算:
2、请你独立完成课本P111练习第1、2题.
3、(1)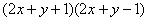 (2)
(2)
(3)4992 (4)1022
4、a2b4-2ab2+1等于( )
A.(ab2-1)2 B. (ab2+1)2 C. (a2b2-1)2 D. (-ab2-1)2
六、中考链接:
1、已知(a+b)2 =11, (a-b)2 =7,则ab的值为
2、若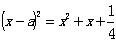 ,则
,则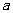 =
=
3、若(x-y)2 +N= x2+xy+y2 ,则N等于( )
七、教学反思;
因式分解(一)
一、学习目标
1.了解因式分解的意义,并能够理解因式分解与多项式乘法的区别与联系.
2.会用提公因式法进行因式分解.
3.树立学生全面认识问题、分析问题的思想,提高学生的观察能力、逆向思维能力.
二、学习重点:掌握提取公因式,公式法进行因式分解.
学习难点:怎样进行多项式的因式分解,如何能将多项式分解彻底.
三、自主学习:
问题一:1. 回忆:运用前两节所学的知识填空:
(1)2(x+3)=___________________;
(2)x2(3+x)=_________________;
(3)m(a+b+c)=_______________________.
2.探索:你会做下面的填空吗?
(1)2x+6=( )( );
(2)3x2+x3=( )( );
(3)ma+mb+mc=( )2.
3.归纳:把一个多项式化为几个整式的乘积形式,这就是因式分解(也叫分解因式).
4.反思:①分解因式的对象是______________,结果是____________的形式.
②分解后每个因式的次数要 (填“高”或“低”)于原来多项式的次数.
四、互动学案:
问题二:1.公因式的概念.填空:
①多项式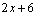 有 项,每项都含有 , 是这个多项式的公因式.
有 项,每项都含有 , 是这个多项式的公因式.
②3x2+x3有 项,每项都含有 , 是这个多项式的公因式.
③ma+mb+mc有 项,每项都含有 , 是这个多项式的公因式.
※多项式各项都含有的 ,叫做这个多项式各项的公因式.
2.提公因式法分解因式.
如果一个多项式的各项含有公因式,那么就可以 ,从而将多项式化成两个 的乘积的形式,这种分解因式的方法叫做提公因式法.如:ma+mb+mc=m(a+b+c)
3.辨一辨:下列各式从左到右的变形,哪是因式分解?
(1)4a(a+2b)=4a2+8ab; (2)6ax-3ax2=3ax(2-x);
(3)a2-4=(a+2)(a-2); (4)x2-3x+2=x(x-3)+2.
(5)36 (6)
(6)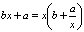
4. 试一试: 用提公因式法分解因式:
(1)3x+6=3( ) (2)7x2-21x=7x( )
(3)24x3+12x2 -28x=4x( ) (4)-8a3b2+12ab3c-ab=-ab( )
5.公因式的构成:①系数:各项系数的最大公约数;②字母:各项都含有的相同字母;③指数:相同字母的最低次幂.
6.方法技巧: (1)、用提公因式法分解因式的一般步骤:a、确定公因式b、把公因式提到括号外面后,用原多项式除以公因式所得商作为另一个因式.
(2)、为了检验分解因式的结果是否正确,可以用整式乘法运算来检验.
问题三:1.把下列多项式分解因式:
(1)-5a2+25a (2)3a2-9ab
(3)-8m2 n-2mn (4)6a(m-2)+8b(m-2)
四、自主测评:
1.练一练:把下列各式分解因式:
(1)ma+mb (2)5y3-20y2 (3)a2x2y-axy2
(4)-4kx-8ky (5)-4x+2x2 (6)(2a+b)(2a-3b)-3a(2a+b)
(7)2a(y-z)-3b(z-y) (8) 21×3.14+62×3.14+17×3.14
五、教学反思:
公式法
一、学习目标:
1.经历用平方差公式法分解因式的探索过程,理解公式中字母的意义。
2.会用平方差公式法对多项式进行因式分解。
3.体会从正、逆两个方面认识和研究事物的方法。
二、学习重点:应用平方差公式分解因式;
学习难点:正确运用平方差公式进行因式分解.
三、自主学习:
1、复习与交流
(a+2)(a-2)= (-x+3)(-x-3)= (3a+2b)(3a-2b)=
2.公式法分解因式在此公式是指什么公式?
3.什么条件下可以用平方差公式进行因式分解?
4.如何将多项式x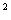 -1和9x
-1和9x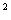 -4分解因式?
-4分解因式?
四、互动学案:
你能像分解x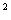 -1和9x
-1和9x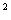 -4一样将下面的多项式分解因式吗?
-4一样将下面的多项式分解因式吗?
⑴p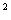 -16= ; ⑵y
-16= ; ⑵y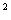 -4= ;
-4= ;
⑶ x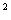 -
-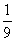 = ; ⑷a
= ; ⑷a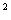 -b
-b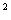 = .
= .
实际上,把平方差公式 (a+b)(a-b)= a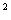 -b
-b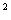
逆过来,就得到 a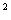 -b
-b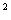 =(a+b)(a-b)。
=(a+b)(a-b)。
那么,一个整式只要表示成两个整式的平方差的形式,就可以用平方差公式分解因式,这种分解因式的方法叫做 。
例1 把下列各式分解因式:
⑴36- a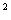 ; ⑵4x
; ⑵4x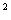 -9y
-9y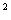 .
.
解:
例2 把下列各式分解因式:
⑴ a3-16a; ⑵2ab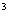 -2ab.
-2ab.
解:
五、自主测评:
1.下列多项式,能用平分差公式分解的是( )
A.-x2-4y2 B.9 x2+4y2
C.-x2+4y2 D.x2+(-2y)2
2.分解因式:2ax2-2ay2=
3.分解因式:x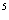 -x
-x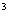 = .
= .

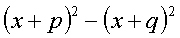 4.分解因式:
4.分解因式:
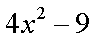 ① ② ③
① ② ③

④ ⑤ ⑥
六、中考链接:
分解因式:
9(m+n)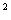 -16(m-n)
-16(m-n)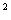 25-(m+2p)2 a
25-(m+2p)2 a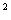 -(a+b)
-(a+b)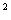
七、小结:
八、教学反思:
