《中心对称》教学案例及反思

一、教材分析

（一）、地位与作用

本节课主要学习中心对称的概念和性质。中心对称是旋转变换的特殊形式，所以已经学过的轴对称变换和旋转的概念及性质，为本节课的学习起了铺垫作用，扫清了学习障碍，本节课的知识也为即将研究的中心对称图形、关于原点对称的点的坐标以及利用平移、轴对称、旋转的组合进行图案设计奠定了坚实的基础。

（二）、教学目标分析

知识与技能:理解中心对称，对称中心，对称点等概念；掌握中心对称的性质；应用中心对称的概念及性质，解决实际问题。

过程与方法:：经历探究发现中心对称性质的过程，提高观察、分析、抽象、概括等能力；体验猜想、类比等数学思想。感悟数学来源于生活，又服务于生活的真谛。

情感态度与价值观：欣赏数学的美学价值，树立学好数学的信心

（三）教学重、难点分析

重点：掌握中心对称的概念及性质

难点：准确理解概念及性质，利用其解决实际问题。

二、教法与学法分析:

（一）、学情分析：本节课是在学生学习了旋转的基础上，从旋转变换引入中心对称的，学生在学习旋转的过程中，已经充分体验了观察、测量、旋转画图等活动，经历了在操作活动中探索性质的过程，获得了初步的数学活动经验和体验，具备了一定的主动参与、合作交流的意识和初步的观察、分析、抽象概括能力。

（二）、教学方法：结合本节课的教学内容，以及学生的心理特点和认知水平，主要采用启发探究和直观演示的教学方法，创设情境启导学生观察、探索、抽象、分析中心对称的概念，揭示刻画中心对称的性质。

（三）学习方法：新课标明确提出要培养“可持续发展的学生”，因此教师要有组织、有目的、有针对性的引导学生并参入到学习活动中，鼓励学生采用动手实践、自主探索，合作交流的学习方式，培养学生“动手”、“动脑”、“动口”的习惯与能力，使学生真正成为学习的主人。

（四）辅助手段：

利用多媒体教学平台来配合教学，就可以把抽象的内容变得更具体，为学生提供丰富的感知材料，培养学生数学直觉能力。

三、教学过程

（一）探究问题，形成概念

第一步：为了使学生关注到概念的实际背景，首先利用多媒体演示2组图片的运动过程，并提出如下问题，力图在课一开始就紧紧抓住学生。

问题1：观察下面的2组图形，看一看各组中2个图形的形状、大小是否相同？怎样将一个图形旋转得到另一个图形？

很自然的从旋转变换的角度引入本节课题：中心对称。让学生体会到知识间的内在联系，中心对称实际上是旋转变换的一种特殊形式，渗透了从一般到特殊的数学思想方法。

第二步：教师再次展示一组图片，演示旋转的过程，进一步提出问题，给学生一定的思考和讨论的空间。接下来从具体图案中抽象出两个三角形，提问：

问题2： (1)把其中一个图案绕点O旋转180°,你有什么发现?

(2)线段AC，BD相交于点O，OA=OC，OB=OD．把 △OCD绕点O旋转180°,你有什么发现?

引导学生分析问题，从而把以下三点逐一击破：1、两个图形；2、（选定）一个点；3、两个图形，一个图形绕着某个点旋转180°后能与另一个图形重合。

（二）探索研究，归纳性质

第一步：为了让学生在理解概念的同时，探索发现中心对称的性质。教师引导学生动手操作，完成63页探究：旋转三角板，画关于点O对称的两个三角形。然后利用画好的学具，分别连接对应点AA’、BB’、CC’。提问：

（1）点O在线段AA’上吗？如果在，在什么位置？

（2）△ABC与△A’B’C’有什么关系？

（3）你能从中得到什么结论？

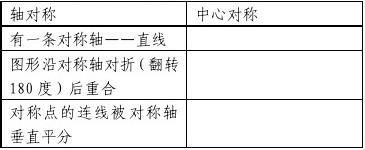
第二步：为了更好的深化学生对知识的理解，接下来让学生对比中心对称与轴对称的联系与区别，提出问题：中心对称与轴对称有什么区别?又有什么联系?

问题提出后，让学生小组内进行充分的讨论交流，共同完成事先准备好的图表。老师利用投影仪进行展示，并让小组选代表进行说明。对于没有归纳完整的，其他组的同学进行补充，对于完成较好的小组，应给予及时的表扬和鼓励。

（三）问题探索，解释应用

为加深学生对概念和性质的理解，设计了如下例题：求作已知点A关于点O的对称点A′。学生大都能作出点A关于点O的对称点A′，然后请一名学生在黑板上完成线段的中心对称线段的作图，并写出作法。教师利用多媒体进行演示，规范作图步骤。待学生完成作图后，进一步提问：

1、一个点绕对称中心旋转180?，得到的是一个平角，这表示什么？

2、你是如何理解“对称点所连线段都经过对称中心，而且被对称中心所平分”的？

3、怎样作出△ABC关于点O对称的△A′B′C′呢？

问题提出后，适当等待，学生纷纷发表自己的见解,畅谈如何作△ABC关于点O对称的△A′B′C′。

这道题是利用中心对称的性质进行作图，使学生能熟练画出两个关于某点成中心对称的图形，巩固学生的作图能力，向学生渗透应用数学的观念。

第二篇：中心对称与中心对称图形 教学案例

《中心对称与中心对称图形》导学案教学设计与评析

胥浦中学 陈启忠

我设计的导学案的内容是苏科版数学八年级上册第3章《中心对称图形》的第二节《中心对称与中心对称图形》的第一课时。

本节课是第3章第2节的内容，它是八年级几何重要内容之一，这一节课与图形的三种运动（平移、翻折、旋转）之一的“旋转”有着不可分割的联系，通过对这一节课的学习，既可以让学生认识图形的三种基本运动中“旋转”在几何知识中的重要体现，同时也完善了初中部分对“对称图形”（轴对称图形、中心对称图形）的知识讲授，它起到了承上启下的作用，它为后面学习“平行四边形”等内容做了充分准备。我将本节课分为5个环节。

首先我通过导学案的第一个环节：《学生预习》部分让学生复习轴对称有关知识如：两条线段AB与A′B′之间的关系，通过复习旧知可以让学生更好地比照“轴对称”来认识“中心对称”和性质。第一环节由学生课前完成，并在黑板上展示出来。此环节不宜化过多的时间。

其次在第二个部分《教师导学》中由老师根据学生的实际情况，选择本节的重点：成中心对称图形概念及其基本性质，引导学生将预习的课本内容回顾一下，加深学生对所预习的知识的印象。我将引导观察学生所给的两组图形，引出中心对称的概念。这一部分可根据教师对学生的了解，对教材的分析灵活安排时间。学生不易理解的多讲点，简单的就少讲或不讲。原则上以教师精讲为主。

第三部分《小组合作例题》这个环节为学生以小组或学习对子为单位，通过多种形式的自主学习完成例题，并能上黑板展示出合作学习的成果。这一环节的三道例题的选择，我遵循由易到难的原则，让学生一步一步的往上走。使学生掌握中心对称的概念到会运用概念解决实际问题。本环节为一堂课重点，教师应通过多种形式参与学生的自主学习中，引导学生完成学习任务。

第四部分为《总结》，由教师带领学生完成对本节课所学的内容进行梳理、复习能使学生巩固所学知识-成中心对称的性质和成中心对称的图形的画法。总结也可由学生在教师的指导下自主完成。

第五部分《巩固练习》，采用当堂训练的方式，及时反馈学生学习状况，使教学能做到有的放矢；我们采用学生互相检查教师随机检查的方式，这样既可以锻炼学生发现问题的能力，又能使学生通过练习，克服错误。

根据中心对称在初中几何教学中的地位与作用，我制订了如下教学目标：

（一）知识与技能

了解成中心对称及其基本性质；

（二）过程与方法

经历观察、操作、发现、探究成中心对称的有关概念和基本性质的过程。

（三）情感、态度、价值观

培养学生观察能力和动手操作能力，感受对称、匀称、均衡的美感，积累一定的审美体验。

教学重点：成中心对称图形概念及其基本性质探索。设计的理由是：掌握概念是探究性质的前提，是应用的基础。只有充分理解了概念，才能更进一步的判定图形是否为中心对称；才能更好的探索性质，才能利用性质学习画已知图形关于某一点的对称图形；才能已经知道中心对称的两个图形找到对称中心。

难点是中心对称的性质及成中心对称的图形的画法。设计的理由是：中心对称性质的获得过程教科书中仅用了一段文字，很少的篇幅，对于这个性质，不是要学生死记硬背，而是要学生具备一定的探究归纳能力，借助运用已学习的旋转性质特征来得出.这对八年级的学生来说，有一定的难度。为了让学生突破难点，授课时采取以学生自主探索和教师导学时画一次，以帮助学生理解和发现性质。

本节课我通过复习图形轴对称，并与中心对称比较，渗透类比的思想方法；用运动的观点观察和认识图形，渗透旋转变换的思想。在实际教学中从生活实例引入，从几何图形引入，让学生通过观察与思考自己总结出中心对称的概念和性质。这样知识点学生掌握比较牢靠。本节课也有比较遗憾的地方：如从课堂反馈来看，教学目的基本达到。不足在于没有给学生多一点时间，再画一个图形巩固一下，以至于后面完成练习的时候，不够熟练。还有课堂提问层次性不突出，今后会多利用设问、反问引导学生，尽量学会放手，激发学生的活力，培养学生自信，让学生敢于表现自己、展现自己。

20xx年9月

课题:§3.2中心对称与中心对称图形（1） 课型：新授课 设计者：陈启忠 学习目标:

1、了解成中心对称及其基本性质；

2、经历观察、操作、发现、探究成中心对称的有关概念和基本性质的过程，培养学生观察能力和动手操作能力，感受对称、匀称、均衡的美感，积累一定的审美体验。

教学重点：成中心对称图形概念及其基本性质探索

教学难点：中心对称的性质及成中心对称的图形的画法

一、学生预习

☆1、已知三点A、B、O．如果点A′与点A关于点O对称，点B′与点B关于点O对称，?

那么线段AB与A′B′的关系是________．

☆2、已知线段AB与点O的位置如图所示，试画出线段AB关于点O的对称线段A′B′．

A

(2)(1)

二、教师导学

观察图形，引出概念：

如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称， 这个点叫做对称中心，两个图形中的对应点叫做对称点。

三、小组合作例题：

☆例1、如图（1），已知△ABC和点O

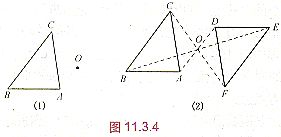
，画出△DEF

，使△DEF和△ABC关于点O成中心对称。

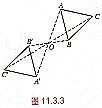
☆例2、△A′B′C′与△ABC关于点O是成中心对称的，你能从图中找到哪些等量关系？

点A绕中心点O旋转180后到点A′，于是A、O、A′三点在一直线上，并且AO＝OA′，另分别在?

一直线上的三点还有__________，__________；并且BO＝___________，CO＝_____________

☆☆例3、如图所示的两个图形成中心对称，你能找到对称中心吗？

四、总结：

1、成中心对称的性质：

在成中心对称的两个图形中，连结对称点的线段都经过________ ，并且被对称中心________ 。 反过来，如果两个图形的对应点连成的线段都经过某一点，并且被平分，那么这两个图形一定关于这一点成中心对称。

⒉、成中心对称的图形的画法（学生自己总结）

3

五、巩固练习：

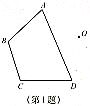
☆1、如图，已知四边形ABCD和点O，画四边形A′B′C′D′，

使四边形A′B′C′D′和四边形ABCD关于点O成中心对称。

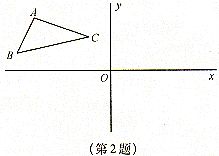
☆2、如图，已知△ABC和过点O的两条互相垂直的直线x、y，

（1）画出△ABC关于直线x对称的△A′B′C′

（2）再画出△A′B′C′关于直线y

对称的△A″B″C″

（3）△A″B″C″与△ABC是否关于点O成中心对称？

六、作业：

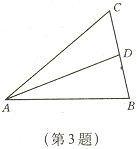
☆1、关于某一点成中心对称的两个图形，对称点所连的线段被________ 平分，对应线段平行且_________。 ☆☆2、如图，已知AD是△ABC的中线，画出以点D为对称中心，与△ABD成中心对称的三角形。

七、回顾反思：

我的收获：_______ ___________________________________________________________。