《平行四边形的判定》教学反思
巴庙初中 唐必坤
上周我们数理化组开展了赛教活动,我以《平行四边形的判定》上了一节公开课,本节课我采用的是“先学后教,当堂训练”的模式教学方法是采用“目标──问题”的教学方法,力求体现“主体参与、自主探索、合作交流、指导引探”的教学理念。
教学从复习平行四边形的定义开始,接着以一个练习题为平台复习平行四边形有哪些重要性质?
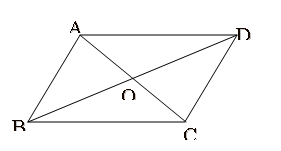 在□ABCD中,AC、BD交于点O问:
在□ABCD中,AC、BD交于点O问:
CD=________BC=________
∠BAD=____∠ADC=____
AO=________BO=________
请从边、角、对角线三方面来回顾。从边考虑:两组对边分别平行,两组对边分别相等;从角考虑:两组对角分别相等;从对角线考虑:两条对角线互相平分。
接着引入新课,课件展示教学目标,并要求学生根据自学要求展开自学,理解并学会平行四边形的两个判定,然后用两个练习题来检测,巩固学生对于两个判定定理的推论过程的理解以及运用。接着话锋一转,出示例题:
如图,在平行四边形四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形

在引导学生求证的时候,我鼓励他们用多种方法去证明。在巡视检查的过程中,我找了三名同学将他们三种不同的方法展示在黑板上。具体如下
方法(一)
证明:
∵四边形ABCD是平行四边形
∴AD BC,∠B= ∠D,AB=CD
∵AF=EC
∴AD-AF=BC-EC
即BE=DF
∴⊿ABE≌⊿CDF(SAS)
∴ ∠AEB=∠DFC
∵AD∥BC
∴ ∠DFC=∠FCB
∴ ∠AEB=∠FCB
∴AE∥CF
又AF∥EC
∴四边形AECF是平行四边形(两组对边分别平行的四边形是平行四边形)
方法(二)
证明:
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠B= ∠D
即∵AF=EC
∴AD-AF=BC-EC
即BE=DF
∴⊿ABE≌⊿CDF(SAS)
又∴AE=CF
∴四边形AECF是平行四边形(两组对边分别相等的四边形是平行四边形)
方法(三)
证明:∵四边形ABCD是平行四边形
∴AD∥BC
即AF∥CE
又∵AF=CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
(在这部分教学中我有意识的创造让学生探究的时间和空间,这有利于学生的持续发展。对于例题结论的证明,我引导学生将自己学得的判定方法进行对比和筛选,进行一题多解,便于思维发散,不把思路局限在某一判定方法上,同时还让学生进一步思考:由已知条件你还可得出哪些结论?从而使学生养成良好的思维习惯,提高他们的认知水平。)
在本节课的教学过程中,虽然学生的数学基础不是很好,但学生的思维始终保持着高度的活跃性,出现了很多的闪光点,对我的启发也很大,真可谓教学相长。数学的学习要重视学习方法的指导,知识的真正获得不是靠知者的“告诉”而是在于学习者的亲身体验所得,这是我的心得体会。在以后的日常教学中,我将牢记这两点,真正使学生能力得以培养,技能逐步形成,数学素质得到提高。
第二篇:平行四边形的判定(1)及教学反思
18.1.2平行四边形的判定1
学习目标:1.在探索平行四边形的判定条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
学习重点:平行四边形的判定方法及应用.
学习难点:平行四边形的判定定理与性质定理的灵活应用.
学习过程:
一、温故知新
 1、有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你能帮它补好吗?
1、有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你能帮它补好吗?
2、平行四边形性质:
1.)从边上看: .
在 ABCD中:
ABCD中:
∥ . ∥ .
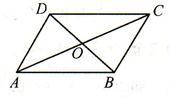 = . = .
= . = .
2.)从角上看: .
在 ABCD中: = , = ,
ABCD中: = , = ,
+ =180°. + =180°.
3.)从对角线上看: .
在 ABCD中: = , = 。
ABCD中: = , = 。
3.平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
二、自主探究,
先自学课本45页,再推理论证,最后同桌前后桌同学交流合作解疑:
1.如图,将两长两短的四根细木条用小钉合在一起,做成一个四边形,使等长的木条成为对边,转动这个四边形,使它形状改变.在图形变化的过程中,它一直是一个平行四边形吗?

 已知:如图,在四边形ABCD中,AD=CB,AB=CD
已知:如图,在四边形ABCD中,AD=CB,AB=CD
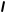


 求证:四边形ABCD是平行四边形。
求证:四边形ABCD是平行四边形。
由上面的证明你得到了什么结论?
平行四边形判定定理1:
符号语言:
2.如图所示,∠A=∠C,∠ADC=∠ABC,问四边形ABCD是不是平行四边形.
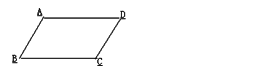
由上面的证明你得到了什么结论?
平行四边形判定定理2:
符号语言:
3.如图,将两根细木条AC,BD的中点重叠,用小钉绞合在起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?
已知:如图,四边形ABCD的对角线AC,BD相交于点O,并且 AO=CO,BO=DO。
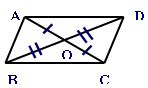 求证:四边形ABCD是平行四边形。
求证:四边形ABCD是平行四边形。
由上面的证明你得到了什么结论?
平行四边形判定定理2:
符号语言:
4.总结归纳判定平行四边形的方法:
 三、理解运用,拓展提高
三、理解运用,拓展提高
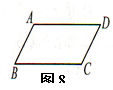
1.如图8,四边形ABCD中
⑴若AB∥CD,补充条件____________, 使四边形ABCD为平行四边形。
(2)若AD=CB,补充条件____________,使四边形ABCD为平行四边形。
2.如图13,若AD=8cm, AB=4cm,那么当BC= cm,
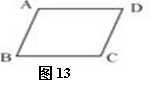 CD= cm时, 四边形ABCD是平行四边形.
CD= cm时, 四边形ABCD是平行四边形.

3.如图14,AD=BC=16, AB=CD=EF=15, CF=DE=9,图中互相平行的线段有
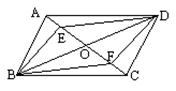 4.已知:如图平行四边形ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF.
4.已知:如图平行四边形ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
四、知识点小结:本节课我们学习了……..
平行四边形的性质及判定方法的归纳:
五、限时检测(10分钟)
1. 师生共练,简单应用
 判断下列四边形是否为平行四边形?并说出你的依据.
判断下列四边形是否为平行四边形?并说出你的依据.
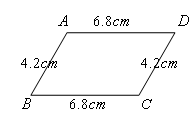

2.已知:平行四边形ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证:EO=OF.
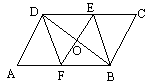
 3.已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN,且BM=DN.
3.已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN,且BM=DN.
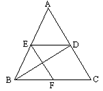 4.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC, 求证:BE=CF
4.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC, 求证:BE=CF
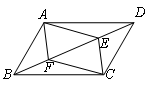 5、如图所示,在□ABCD中,E、F是对角线BD上两点,且BF=DE,连接AE、CE、AF、CF,求证:四边形AECF是平行四边形.
5、如图所示,在□ABCD中,E、F是对角线BD上两点,且BF=DE,连接AE、CE、AF、CF,求证:四边形AECF是平行四边形.
作业
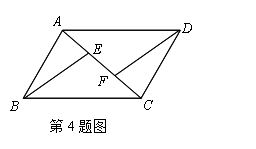
 1、已知:如图,在四边形ABCD中,AB=CD,AD=BC,点E、F分别在BC和AD边上,AF=CE,EF和对角线BD相交于点O,求证:点O是BD的中点.
1、已知:如图,在四边形ABCD中,AB=CD,AD=BC,点E、F分别在BC和AD边上,AF=CE,EF和对角线BD相交于点O,求证:点O是BD的中点.
2.如图,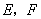 是平行四边形
是平行四边形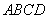 的对角线
的对角线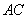 上的点,
上的点, .请你猜想:
.请你猜想: 与
与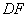 有怎样的位置关系和数量关系?并对你的猜想加以证明。
有怎样的位置关系和数量关系?并对你的猜想加以证明。
教学反思
本节课充分激发学生学习数学的兴趣,让学生积极参与、讨论,导中有练、有思、有研,改进教师先讲知识,然后再进行强化训练的做法,使讲、练、思、研融合在一起,整节课学生能始终处于思维活跃状态,让学生充分体会快乐学习。
在这节课的教学过程中,学生的思维始终保持着高度的活跃性,出现了很多的闪光点,对我的启发也很大,真可谓教学相长。所以在教学过程中教师应积极转变传统的“传道、授业、解惑”的角色,在教学中应把握教材的精神,在设计、安排和组织教学过程的每一个环节都应当有意识地体现探索的内容和方法,避免教学内容的过分抽象和形式化,使学生通过直观感受去理解和把握,体验数学学习的乐趣,积累数学活动经验,体会数学推理的意义,让学生在做中学,逐步形成创新意识。
