Strongart的blog: 萌男哲学家与宅男大学教授 blog地址:.cn/strongart
Strongart个人成就大盘点“
哲学方面:Strongart提出了一些非常精深的哲学命题,比如“思想先于立场”、“文本就是流形”、“矛盾就是效果”等等,此外还给出了“自我免疫说”、“历史骗局说”等哲学思想,从人类的元精神划分了硬哲学与软哲学,对电脑文件的同一性问题做了专门研究。他已经完成了其哲学体系《作为矛盾与表象的世界》的初稿,正在连载的Strongart如是说哲学随笔也已有近百段,其他像随笔评论之类的哲理文章更是不计其数,同时还录制了一批非常具有思想性的哲学讲座,比如辩证法其实是脑残哲学、哲学王其实只是土著的幻想等等。
文学方面:Strongart早年曾创作哲理荒诞小说《微积分的泡沫》,后来开始撰写一系列的哲理童话,比如黑色童话皮皮的故事系列,猫死国的故事系列、上帝与土著人系列等等,还有批判传统文化的丑陋的C国人杂文系列,其中的一些作品可以说是名著级的。此外,他还写了很多书评读后感之类的文章,表达了自己对文学艺术的独特见解。
数学方面:Strongart在数学上提出了数学族命题纲领,提出了流体数学与模型数学的新概念,在方法论上给出了MLMA大法,还新定义了Noether算子、Artin算子,S-除子等全新的数学概念。他写了很多高端数学书籍的读后感,对其中数学思想大都有个人独到的见解,同时正在制作的法式特色数学讲座,目前研究生级的交换代数1-30已经完结,正在更新泛函分析新课。
艺术方面:Strongart绘制了一些抽象艺术图片,比如赤裸的黑暗、饥饿的月亮都是其中的神作,同时还录制了一些行为艺术视频,比如王老吉泡咖啡、哲学家的人间食粮等等。当然,他最擅长还是语言艺术,像中国名著与日本动漫、原来我犯了第二十二条军规,都可以视为其讲座节目的经典代表,此外还有想象力丰富的染皮肤系列、海贼王恶魔果实系列作品,也都散发着独特的艺术魅力。
对于一个普通的中国教授,只要有其中的一两项成就,大概就可以说是比较优秀的人才了。但对于哲学家Strongart,博客里的这些成就还只是冰山一角,更多的内容需要等恢复名誉后才能完全展现,现在他就好比是一个深不可测的优质金矿,等待着各位有识之士前来开采,当然可持续发展也是不能忘记的哦~
第二篇:Strongart数学笔记:高中以后学什么数学
高中以后学什么数学
如果你喜欢数学,那么上大学就一定要报数学专业,其他专业即使是理工科的,学的高等数学之类也仅仅是一层皮毛。除非你能够顽强的自学,否则你的数学生涯就GAMEOVER了。当然,即使你报了数学专业,到最后还是要依靠自学。从这个意义上来说,报什么专业就真的无所谓了,只要负担轻就OK了。
下面的图表简单罗列了高中以后的数学到底可以走到哪里(并未涉及数论、集合论之类的另类领域),也许你会感到有点恐怖,其实我大学时数学大致就学了这些:因为那时候没有人交流,也不是太懂得节约时间。可遗憾的是有些不怎么认真数学专业研究生,也无非是在一两个方向入门罢了:
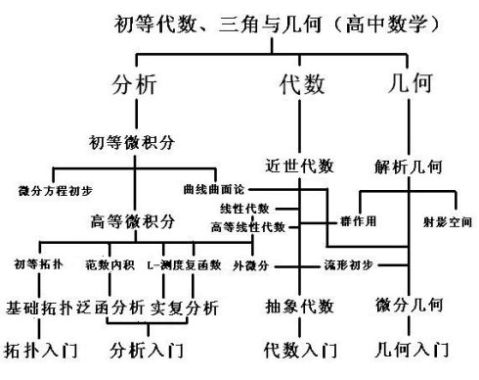
高中以后的数学(当然是专业的)课程要大致由三个部分组成,分析、代数和几何,但我认为现行的教育安排是非常失衡的。大致说来是,数学分析太臃肿,高等代数没前途,解析几何又太狭隘。下面我就结合自己的经历来谈谈这个问题:
先来看分析,很多同学都认为数学分析难学,因为它涉及的东西太多太琐碎了。既有各种初级计算技巧,甚至包括近似估计;又有深刻的理论推导,有时还一些先进的思想压缩到初步的理论中,却不能充分展开。我那时就是疲于应付,最后还是不得不退化为微积分,却又往往有所顾及,不像头脑简单的时候可以肆无忌惮的享受着计算的快乐。其实实数公理部分的不少证明细节得到平面点集拓扑才能充分展开(毕竟圆盘的覆盖要比区间的覆盖更加直观一些),又如像一致
收敛这样的概念到函数空间中用确界范数才能自然理解的,而这一切都被压缩到数学分析之中。
要解决这个困难,比较方便的办法的把数学分析分成两个部分,初等的部分相当于稍微严格的微积分,还可以把初步的微分方程与曲线曲面理论放入其中,重在对具体问题的解决与计算技术的熟练化(以后就用不着再害怕计算了)。我想,在彻底严格化之前先做一番计算练习,这应该是非常有趣的。等有了这样的微积分基础之后,同时严格抽象的思想也已经从代数学中建立起来,这是就可以把它们汇合起来,向分析的主干挺进。此时的自由度也相应提高,再介绍一点初等拓扑、范数内积、Lebesgue积分、外微分什么的也都是不错的课题,对多变量的情形也可以用向量来统一处理,甚至还可以把关于复函数的初步理论吸收进来。
然后看代数,高等仿佛没有什么后续课程的支持,矩阵论似乎往往与近似计算结合起来,从而更侧重应用。所以如果说到基础的话,无无疑应该是抽象代数才对。如果四年学下来,就大致了解一些群、环、域,没看到后面更加精彩的内容,恐怕就非常可惜了。我认为为高等代数应该被吸收到抽象代数里,数学专业的代数学一开始就应该讲群,让学生看到数学结构是怎样抽象出来的,也能熟悉如何在抽象的基础上分析问题。这里选代数作为培养抽象思想的突破口是因为它比较纯洁,不像分析那样依赖很多计算,而且也不用多少背景知识。如果以后再处理初等材料的话,自然就有居高临下的优越感,而线性
代数的主要部分自然可以在模的角度来统一处理(高等线性代数),具体依赖数域的部分则可以作为专题——有所得就有所失,抽象也不是万能的啊!此外,先介绍群还可以作为几何学的预备知识。当然,一开始的介绍不宜太深入,作为基础至多到Sylow定理就可以了,后面还有专门的异常丰富的抽象代数课程呢。
几何的话,很多人认为入门的几何就是解析几何,但现有解析几何往往只是在熟悉常见曲面方程。其实,解析几何的概念可以推广至微分几何之前几何(包括现在所谓高等几何中非介绍性的部分),其要点在于强调群作用观点与射影空间的直观。群作用观点可以给出几何学的大体的框架,让我们知道自己是在什么舞台上活动,这样的舞台可以一直渗透到微分几何中。射影空间则可以与熟悉欧式空间相类比,对以后的代数几何也是一种直观,否则我们往往无从得知自己的把什么东西在代数化。比如我那时没注意射影几何,看到“P^2的任意两条直线都是相交的”的时候,就感到无所适从了。
微分几何一定要尽早介绍流形,其实放到第一章也是无妨的。在熟悉了平直的欧式空间之后(多变量分析),推广到一般的流形上也是大势所趋,并没有什么太大的跳跃。此后就可以在这样框架下介绍直线与曲面,其实R^3中的很多问题在一般的空间中一样可以处理(比如测地线方程之类都是差不多的),像高中那样用两年时间研究平面二次曲线(还不包括一般理论)实在是太奢侈了。如果在R^3中有趣的东西都可以专门处理,也可以让大家清楚到底它们为什么是有趣
的。记得我那时R^3的微分几何都忘得差不多了,黎曼几何不也一样在学嘛。
其实,有些观点高的东西并不一点是难学的,有的东西难学恰恰是用低观点来解决高级领域的问题造成的。也许又有人会谈基础的重要性,但真要强调基础的话,各人的基础都是相对有差异的,不排除某些牛人能把范畴同调之类的作为他自己的基础。合理的学习路径应该是从最容易入手的地方切入,看看最后究竟能够走到哪里,所以不要让我们的学生长时间滞留那些初等的领域。只要有可能,就要尽可能的扩展与深入,然后才能找到自己的基础,并且在这样基础上继续前进,毕竟上面的那张宏伟的图表也仅仅是入门而已。
本文作者Strongart是一位自学数学的牛人,现在他依然努力坚持自学数学,似乎又有了新的突破,还录了一些数学专业教学视频放在网上。然而,他却一直没有收到专业人士的邀请,至今只能依靠网络书店购买书籍,无法获取海量的论文资料,也没有机会和一流的学者们交流,最后只能走上娱乐拯救学术的道路,这不论对他自己还是对中国的数学事业都将是一个损失。这里我希望一些有识之士能够用自己的实际行动支持一下!
欢迎大家二次分享此文档,请注明文档作者Strongart,欢迎访问。
