【例1】(20##全国大纲卷理22)函数 ,定义数列
,定义数列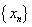 如下:
如下: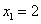 ,
,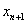 是过两点
是过两点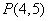 、
、 的直线
的直线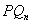 与
与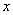 轴交点的横坐标.
轴交点的横坐标.
(1)证明: ;
;
(2)求数列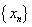 的通项公式.
的通项公式.
【证】(1)证:直线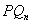 的方程为
的方程为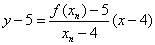 ,即
,即 ,
,
令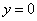 ,解得
,解得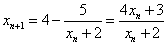 .
.
下用数学归纳法证明 :
:
① 当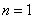 时,
时,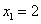 ,所以
,所以 .
.
② 假设当 时结论成立,即
时结论成立,即 ,则当
,则当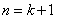 时,
时,
由 ,得
,得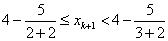 ,即
,即 ,故
,故 .
.
由①②知,对一切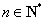 都有
都有 .
.
从而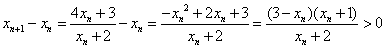 ,故
,故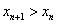 .
.
综上, .
.
(2)解:由(1)知,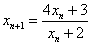 ,则
,则 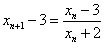 ①,
①,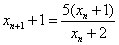 ②,
②,
①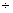 ②,得
②,得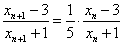 ,故数列
,故数列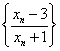 是首项为
是首项为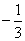 ,公比为
,公比为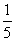 的等比数列.
的等比数列.
因此,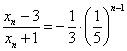 ,解得:
,解得: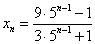
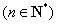 .
.
【例2】已知函数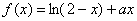 在开区间(0,1)内是增函数.
在开区间(0,1)内是增函数.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若数列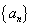 满
满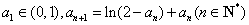 ,证明:
,证明: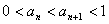 .
.
(Ⅰ)解: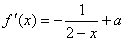 ,由于f (x)在(0,1)内是增函数,
,由于f (x)在(0,1)内是增函数,
∴ 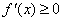 ,即
,即 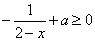 在x∈(0,1)时恒成立.
在x∈(0,1)时恒成立.
∴  恒成立,
恒成立,
而 -2<x-2<-1,
∴ 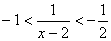 ,
,
即 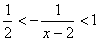 ,
,
∴ 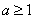 即为所求.
即为所求.
(Ⅱ) 证明:① 当n=1时,由题设知a1∈(0,1).
② 假设当n=k时,不等式成立,即ak∈(0,1),则
当n=k+1时,由(Ⅰ)知,f(x)=ln(2-x)+x在(0,1)上是增函数
∴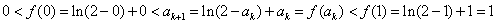 ,
,
即ak+1∈(0,1),故n=k+1时命题成立.
根据① ② 知0<an<1,n∈N*.
又 ∵  ,
,
∴ 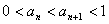 .
.
【例3】已知函数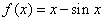 ,数列{
,数列{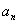 }满足:
}满足: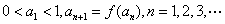 ,证明:
,证明:
(Ⅰ) 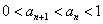 ;(Ⅱ)
;(Ⅱ) 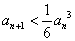 .
.
证明:(Ⅰ) 先用数学归纳法证明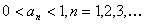
① 当n=1时,由已知,结论成立.
② 假设当n=k时结论成立,即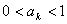 ,
,
因为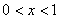 时,
时,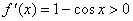 ,
,
所以 在(0,1)上是增函数,又
在(0,1)上是增函数,又 在[0,1]上连续,
在[0,1]上连续,
从而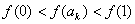 ,即
,即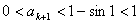 ,
,
故当n=k+1时,结论成立.
由①②可知,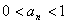 对一切正整数都成立.
对一切正整数都成立.
又因为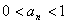 时,
时,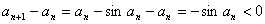 ,
,
所以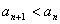 ,综上所述
,综上所述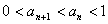 .
.
(Ⅱ) 设函数 ,
,
由(Ⅰ)可知,当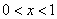 时,
时,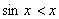 .
.
从而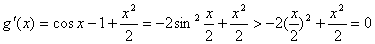 ,
,
所以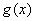 在(0,1)上是增函数.
在(0,1)上是增函数.
又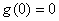 ,
,
所以当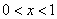 时,
时,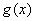 >0成立.
>0成立.
于是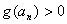 ,即
,即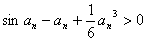 ,
,
故 .
.
【例4】已知函数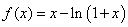 ,数列
,数列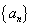 满足
满足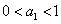 ,
,  ; 数列
; 数列 满足
满足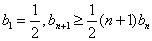 ,
, 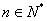 .求证:
.求证:
(Ⅰ)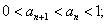
(Ⅱ)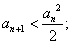
(Ⅲ)若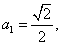 则当n≥2时,
则当n≥2时,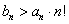 .(
.( 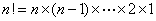 )
)
解: (Ⅰ)先用数学归纳法证明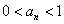 ,
,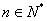 .
.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即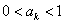 .则当n=k+1时,因为0<x<1时,
.则当n=k+1时,因为0<x<1时,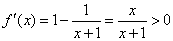 ,所以f(x)在(0,1)上是增函数.
,所以f(x)在(0,1)上是增函数.
又f(x)在 上连续,所以f(0)<f(
上连续,所以f(0)<f(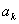 )<f(1),即0<
)<f(1),即0<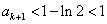 .
.
故当n=k+1时,结论也成立. 即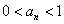 对于一切正整数都成立.
对于一切正整数都成立.
又由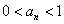 , 得
, 得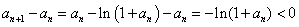 ,从而
,从而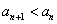 .
.
综上可知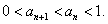
(Ⅱ)构造函数g(x)= -f(x)=
-f(x)= 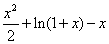 , 0<x<1,
, 0<x<1,
由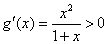 ,知g(x)在(0,1)上增函数.又g(x)在
,知g(x)在(0,1)上增函数.又g(x)在 上连续,所以g(x)>g(0)=0.
上连续,所以g(x)>g(0)=0.
因为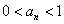 ,所以
,所以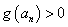 ,即
,即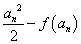 >0,从而
>0,从而
(Ⅲ) 因为 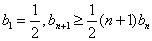 ,所以
,所以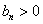 ,
,
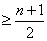 ,
,
所以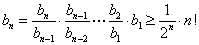 ————①
————①
由(Ⅱ)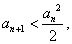 知:
知: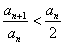 , 所以
, 所以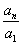 =
=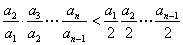 ,
,
因为 , n≥2,
, n≥2, 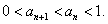
所以 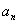
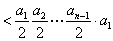 <
< <
< =
=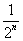 ————② .
————② .
由①② 两式可知: 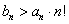 .
.
【例5】 设函数 与数列
与数列 满足以下关系:
满足以下关系:
① 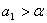 ,其中
,其中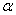 是方程
是方程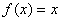 的实根;
的实根;
② 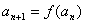 ;
;
③  的导数
的导数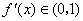 .
.
(Ⅰ) 求证: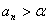 ;
;
(Ⅱ) 判断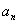 与
与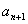 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(Ⅰ) 证:① 当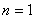 时,
时,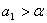 ,不等式成立.
,不等式成立.
② 假设当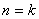 时不等式成立,即
时不等式成立,即 ,则
,则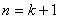 时,
时,
∵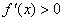 ,则
,则 递增.
递增.
∴ ,即
,即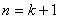 时不等式也成立.
时不等式也成立.
由①、②知,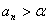 对一切
对一切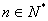 都成立.
都成立.
(Ⅱ) 解: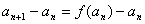 ,
,
设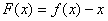 ,则
,则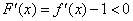 ,
,
∴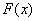 递减,而
递减,而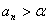 ,
,
∴ ,
,
即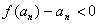 ,亦即
,亦即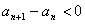 ,
,
∴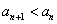 .
.
【例6】(2005江西)已知数列
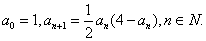
(1)证明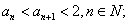
(2)求数列 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,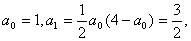 ∴
∴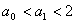 ,命题正确.
,命题正确.
2°假设n=k时有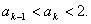
则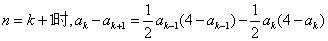
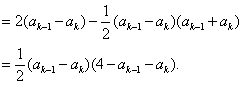
而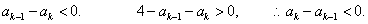
又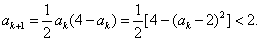
∴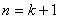 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时,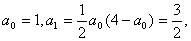 ∴
∴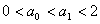 ;
;
2°假设n=k时有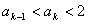 成立,
成立,
令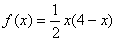 ,
, 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: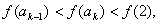 即
即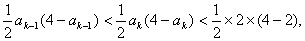
也即当n=k+1时  成立,
成立,
所以由1°、2°知,对一切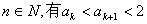
(2)下面来求数列的通项: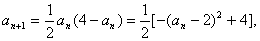 所以
所以
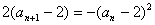
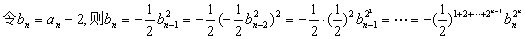 ,
,
又bn=-1,所以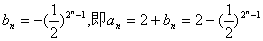
【拓展题】
【例】、数列 满足
满足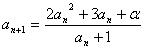 ,且
,且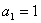 .(1)当
.(1)当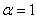 时,求数列
时,求数列 的通项公式;
的通项公式;
(2)若不等式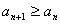 对一切
对一切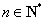 恒成立,求
恒成立,求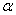 的取值范围;
的取值范围;
(3)当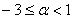 时,证明:
时,证明: .
.
解:(1)当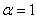 时,
时, .
.
(2)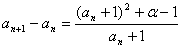 ①,要使
①,要使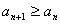 对一切
对一切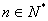 恒成立,
恒成立,
至少需使 成立
成立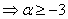 .
.
下面先用数归法证明:当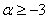 时,
时,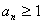 (略),再由①知
(略),再由①知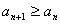 恒成立.
恒成立.
所以 为所求.
为所求.
(3)当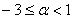 时,由(2)知
时,由(2)知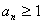 ,则由
,则由
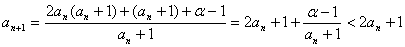
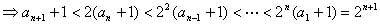
 ,
,
从而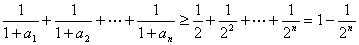 ,等号当且仅当
,等号当且仅当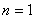 时成立.
时成立.
(2009安徽理21)首项为正数的数列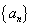 满足
满足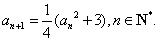 (1)证明:若
(1)证明:若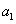 为奇数,
为奇数,
则对一切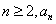 都是奇数;(2)若对一切
都是奇数;(2)若对一切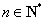 都有
都有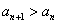 ,求
,求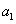 的取值范围.
的取值范围.
略解:(1)已知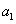 是奇数,假设
是奇数,假设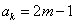 是奇数,其中
是奇数,其中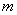 为正整数,
为正整数,
则由递推关系得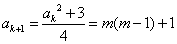 是奇数.(因为
是奇数.(因为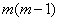 是偶数)
是偶数)
根据数学归纳法,对任何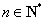 ,
,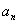 都是奇数.
都是奇数.
(2)(方法一)由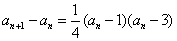 知,
知,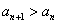 当且仅当
当且仅当 或
或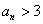 .
.
另一方面,若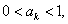 则
则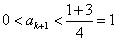 ;若
;若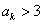 ,则
,则
根据数学归纳法,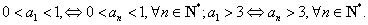
综合所述,对一切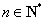 都有
都有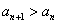 的充要条件是
的充要条件是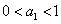 或
或 .
.
(方法二)由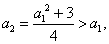 得
得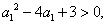 于是
于是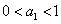 或
或 .
.
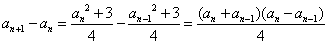 ,因为
,因为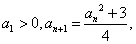
所以所有的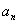 均大于
均大于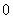 ,因此
,因此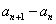 与
与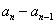 同号.
同号.
根据数学归纳法,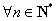 ,
,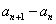 与
与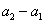 同号.
同号.
因此,对一切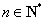 都有
都有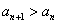 的充要条件是
的充要条件是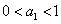 或
或 .
.
第二篇:数学归纳法证明不等式2







