运筹学课程设计

时间：2024.3.31

摘要

目标规划是由线性规划发展演变而来，但比线性规划更加灵活，可以解决多个目标并且还可以自带从属目标的规划问题。是一较之线性规划更接近于实际决策过程的决策工具。本文从某电子厂最优月度计划生产问题”，建立相对应的目标规划模型按多目标的优先级逐级展开，利用目标规划的层次算法，将多目标转化为线性规划，并使用Lindo软件求解该模型。给出为使某电子厂达到最优月度计划生产数字，对生产数量及工作时间做出合理规划方案。然后利用Lingo软件，编程求解运输问题的案例模型，得到最优调运方案。

关键词：目标规划、优先级

一、问题的提出

某工厂生产电视机和DVD播放机两种产品，分别由甲，乙两个车间生产，生产一台DVD播放机需甲车间加工2h，乙车间装配1h，产一台电视机需甲车间加工1h，乙车间装配3h。这两种产品生产出来后均需经检验，销售等环节。已知每台电视机检验销售费用需30元，每台DVD播放机检验销售费用需50元。又甲车间每月可用生产工时为120h，管理费用为80元/h，乙车间每月可用生产工时为150h，管理费用为20元/h。估计每台电视利润为75元，每台DVD播放机利润为100元，有估计一年内平均每月可销售电视机80台，DVD播放机50台。

工厂确定制订月度计划的目标如下：

P1：检验和销售费用每月不超过4600元；

P2：每月售出DVD播放机不少于50台；

P3:甲乙两车间生产工时要得到充分利用；

P4：甲车间加班不超过20小时；

P5;电视机不少于100台；

P6：两车间加班总时间要有控制。

试确定该厂为达到以上目标的最优月度计划生产数字。

二、问题的分析

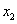设为每月生产DVD播放机的台数，为每月生产电视机的台数，根据题中给出条件，约束情况如下：

（1）甲乙车间可用工时的约束

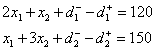
（2）检验和销售费用的限制

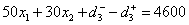
（3）每月销售量要求

（4）对甲车间加班的限制

三、数学模型的建立

将以上约束条件整理得到目标规划数学模型

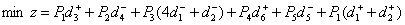
s.t.

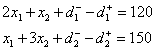
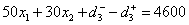
所有变量非负

四、模型的求解

在lindo下按照目标规划的层次算法求解目标规划

P1：输入：

min d3

50x1+30x2+d3_-d3=4600

End

输出：

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D3 0.000000 1.000000

X1 92.000000 0.000000

X2 0.000000 0.000000

D3_ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

NO. ITERATIONS= 0

P2：输入：

min d4_

50x1+30x2+d3_-d3=4600

x1+d4_-d4=50

d3=0

End

输出：

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D3 0.000000 1.000000

X1 92.000000 0.000000

X2 0.000000 0.000000

D3_ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

NO. ITERATIONS= 0

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D4_ 0.000000 1.000000

X1 50.000000 0.000000

X2 70.000000 0.000000

D3_ 0.000000 0.000000

D3 0.000000 0.000000

D4 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

NO. ITERATIONS= 1

P3：输入：

min 4d1_+d2_

50x1+30x2+d3_-d3=4600

x1+d4_-d4=50

2x1+x2+d1_-d1=120

x1+3x2+d2_-d2=150

d3=0

d4_=0

End

输出：

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D3 0.000000 1.000000

X1 92.000000 0.000000

X2 0.000000 0.000000

D3_ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

NO. ITERATIONS= 0

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D4_ 0.000000 1.000000

X1 50.000000 0.000000

X2 70.000000 0.000000

D3_ 0.000000 0.000000

D3 0.000000 0.000000

D4 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

NO. ITERATIONS= 1

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D1_ 0.000000 4.000000

D2_ 0.000000 1.000000

X1 50.000000 0.000000

X2 33.333332 0.000000

D3_ 1100.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 0.000000

D1 13.333333 0.000000

D2 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

5) 0.000000 0.000000

6) 0.000000 0.000000

7) 0.000000 0.000000

NO. ITERATIONS= 1

P4:输入：

min d6

50x1+30x2+d3_-d3=4600

x1+d4_-d4=50

2x1+x2+d1_-d1=120

x1+3x2+d2_-d2=150

d1+d6_-d6=20

d3=0

d4_=0

d1_=0

d2_=0

End

输出：

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D3 0.000000 1.000000

X1 92.000000 0.000000

X2 0.000000 0.000000

D3_ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

NO. ITERATIONS= 0

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D4_ 0.000000 1.000000

X1 50.000000 0.000000

X2 70.000000 0.000000

D3_ 0.000000 0.000000

D3 0.000000 0.000000

D4 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

NO. ITERATIONS= 1

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D1_ 0.000000 4.000000

D2_ 0.000000 1.000000

X1 50.000000 0.000000

X2 33.333332 0.000000

D3_ 1100.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 0.000000

D1 13.333333 0.000000

D2 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

5) 0.000000 0.000000

6) 0.000000 0.000000

7) 0.000000 0.000000

NO. ITERATIONS= 1

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D6 0.000000 1.000000

X1 50.000000 0.000000

X2 33.333332 0.000000

D3_ 1100.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 0.000000

D1_ 0.000000 0.000000

D1 13.333333 0.000000

D2_ 0.000000 0.000000

D2 0.000000 0.000000

D6_ 6.666667 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

5) 0.000000 0.000000

6) 0.000000 0.000000

7) 0.000000 0.000000

8) 0.000000 0.000000

9) 0.000000 0.000000

10) 0.000000 0.000000

NO. ITERATIONS= 0

P5：输入：

min d5_

50x1+30x2+d3_-d3=4600

x1+d4_-d4=50

2x1+x2+d1_-d1=120

x1+3x2+d2_-d2=150

d1+d6_-d6=20

x2+d5_-d5=80

d3=0

d4_=0

d1_=0

d2_=0

d6=0

End

输出：

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D3 0.000000 1.000000

X1 92.000000 0.000000

X2 0.000000 0.000000

D3_ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

NO. ITERATIONS= 0

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D4_ 0.000000 1.000000

X1 50.000000 0.000000

X2 70.000000 0.000000

D3_ 0.000000 0.000000

D3 0.000000 0.000000

D4 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

NO. ITERATIONS= 1

LP OPTIMUM FOUND AT STEP 1

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D1_ 0.000000 4.000000

D2_ 0.000000 1.000000

X1 50.000000 0.000000

X2 33.333332 0.000000

D3_ 1100.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 0.000000

D1 13.333333 0.000000

D2 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

5) 0.000000 0.000000

6) 0.000000 0.000000

7) 0.000000 0.000000

NO. ITERATIONS= 1

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 0.0000000E+00

VARIABLE VALUE REDUCED COST

D6 0.000000 1.000000

X1 50.000000 0.000000

X2 33.333332 0.000000

D3_ 1100.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 0.000000

D1_ 0.000000 0.000000

D1 13.333333 0.000000

D2_ 0.000000 0.000000

D2 0.000000 0.000000

D6_ 6.666667 0.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 0.000000

4) 0.000000 0.000000

5) 0.000000 0.000000

6) 0.000000 0.000000

7) 0.000000 0.000000

8) 0.000000 0.000000

9) 0.000000 0.000000

10) 0.000000 0.000000

NO. ITERATIONS= 0

LP OPTIMUM FOUND AT STEP 3

OBJECTIVE FUNCTION VALUE

1) 40.00000

VARIABLE VALUE REDUCED COST

D5_ 40.000000 0.000000

X1 50.000000 0.000000

X2 40.000000 0.000000

D3_ 900.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 2.000000

D1_ 0.000000 1.000000

D1 20.000000 0.000000

D2_ 0.000000 0.000000

D2 20.000000 0.000000

D6_ 0.000000 1.000000

D6 0.000000 0.000000

D5 0.000000 1.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 -2.000000

4) 0.000000 1.000000

5) 0.000000 0.000000

6) 0.000000 1.000000

7) 0.000000 -1.000000

8) 0.000000 0.000000

9) 0.000000 2.000000

10) 0.000000 0.000000

11) 0.000000 0.000000

12) 0.000000 1.000000

NO. ITERATIONS= 3

P6：输入：

min 4d1+d2

50x1+30x2+d3_-d3=4600

x1+d4_-d4=50

2x1+x2+d1_-d1=120

x1+3x2+d2_-d2=150

d1+d6_-d6=20

x2+d5_-d5=80

d3=0

d4_=0

d1_=0

d2_=0

d6=0

d5_=40

End

输出：

LP OPTIMUM FOUND AT STEP 2

OBJECTIVE FUNCTION VALUE

1) 100.0000

VARIABLE VALUE REDUCED COST

D1 20.000000 0.000000

D2 20.000000 0.000000

X1 50.000000 0.000000

X2 40.000000 0.000000

D3_ 900.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 9.000000

D1_ 0.000000 4.000000

D2_ 0.000000 1.000000

D6_ 0.000000 0.000000

D6 0.000000 0.000000

D5_ 40.000000 0.000000

D5 0.000000 7.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 -9.000000

4) 0.000000 4.000000

5) 0.000000 1.000000

6) 0.000000 0.000000

7) 0.000000 -7.000000

8) 0.000000 0.000000

9) 0.000000 9.000000

10) 0.000000 0.000000

11) 0.000000 0.000000

12) 0.000000 0.000000

13) 0.000000 7.000000

NO. ITERATIONS= 2

RANGES IN WHICH THE BASIS IS UNCHANGED:

OBJ COEFFICIENT RANGES

VARIABLE CURRENT ALLOWABLE ALLOWABLE

COEF INCREASE DECREASE

D1 4.000000 INFINITY 4.000000

D2 1.000000 INFINITY 1.000000

X1 0.000000 INFINITY 9.000000

X2 0.000000 INFINITY 7.000000

D3_ 0.000000 0.180000 0.000000

D3 0.000000 INFINITY 0.000000

D4_ 0.000000 INFINITY INFINITY

D4 0.000000 INFINITY 9.000000

D1_ 0.000000 INFINITY 4.000000

D2_ 0.000000 INFINITY 1.000000

D6_ 0.000000 4.000000 0.000000

D6 0.000000 INFINITY 0.000000

D5_ 0.000000 INFINITY INFINITY

D5 0.000000 INFINITY 7.000000

RIGHTHAND SIDE RANGES

ROW CURRENT ALLOWABLE ALLOWABLE

RHS INCREASE DECREASE

2 4600.000000 INFINITY 900.000000

3 50.000000 0.000000 10.000000

4 120.000000 20.000000 0.000000

5 150.000000 20.000000 INFINITY

6 20.000000 INFINITY 0.000000

7 80.000000 0.000000 6.666667

8 0.000000 0.000000 0.000000

9 0.000000 10.000000 0.000000

10 0.000000 0.000000 0.000000

11 0.000000 0.000000 0.000000

12 0.000000 0.000000 0.000000

13 40.000000 6.666667 0.000000

LP OPTIMUM FOUND AT STEP 2

OBJECTIVE FUNCTION VALUE

1) 100.0000

VARIABLE VALUE REDUCED COST

D1 20.000000 0.000000

D2 20.000000 0.000000

X1 50.000000 0.000000

X2 40.000000 0.000000

D3_ 900.000000 0.000000

D3 0.000000 0.000000

D4_ 0.000000 0.000000

D4 0.000000 9.000000

D1_ 0.000000 4.000000

D2_ 0.000000 1.000000

D6_ 0.000000 0.000000

D6 0.000000 0.000000

D5_ 40.000000 0.000000

D5 0.000000 7.000000

ROW SLACK OR SURPLUS DUAL PRICES

2) 0.000000 0.000000

3) 0.000000 -9.000000

4) 0.000000 4.000000

5) 0.000000 1.000000

6) 0.000000 0.000000

7) 0.000000 -7.000000

8) 0.000000 0.000000

9) 0.000000 9.000000

10) 0.000000 0.000000

11) 0.000000 0.000000

12) 0.000000 0.000000

13) 0.000000 7.000000

NO. ITERATIONS= 2

五、解的分析和结论

经计算得最优解如下：

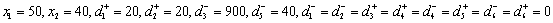
即该厂每月生产DVD播放机50台，电视机40台，利润可达8000元。

一、问题的提出

已知某公司产品的产量，销量和运价（单位：万元/万吨）见表

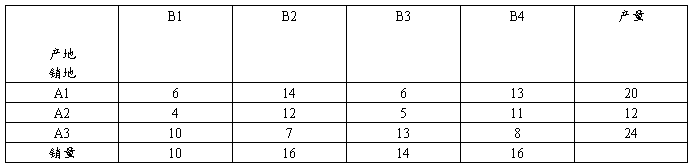
问该公司该如何调运，使总的运费支出最少。

二、数学模型的建立

设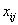为从第i个产地调运给第j个销地的产品数量

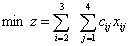
S.t.

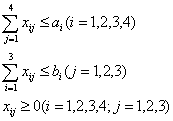
三、模型的求解

使用LINGO软件，编制程序如下：

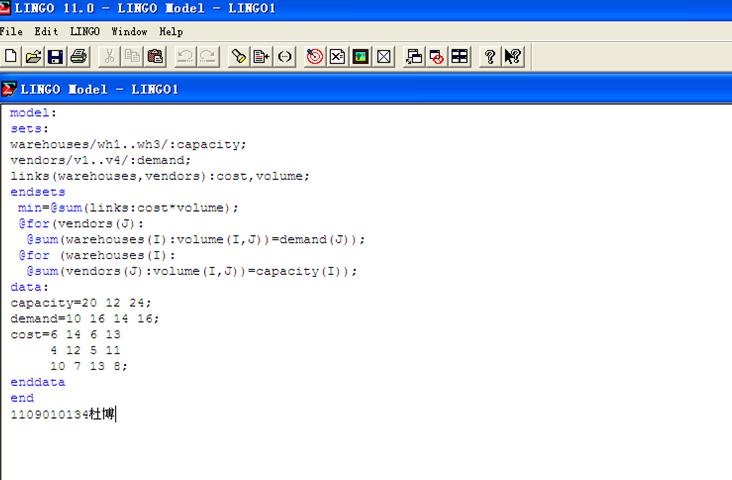
输出：

Global optimal solution found.

Objective value: 400.0000

Infeasibilities: 0.000000

Total solver iterations: 7

Variable Value Reduced Cost

CAPACITY( WH1) 20.00000 0.000000

CAPACITY( WH2) 12.00000 0.000000

CAPACITY( WH3) 24.00000 0.000000

DEMAND( V1) 10.00000 0.000000

DEMAND( V2) 16.00000 0.000000

DEMAND( V3) 14.00000 0.000000

DEMAND( V4) 16.00000 0.000000

COST( WH1, V1) 6.000000 0.000000

COST( WH1, V2) 14.00000 0.000000

COST( WH1, V3) 6.000000 0.000000

COST( WH1, V4) 13.00000 0.000000

COST( WH2, V1) 4.000000 0.000000

COST( WH2, V2) 12.00000 0.000000

COST( WH2, V3) 5.000000 0.000000

COST( WH2, V4) 11.00000 0.000000

COST( WH3, V1) 10.00000 0.000000

COST( WH3, V2) 7.000000 0.000000

COST( WH3, V3) 13.00000 0.000000

COST( WH3, V4) 8.000000 0.000000

VOLUME( WH1, V1) 0.000000 0.000000

VOLUME( WH1, V2) 0.000000 2.000000

VOLUME( WH1, V3) 14.00000 0.000000

VOLUME( WH1, V4) 6.000000 0.000000

VOLUME( WH2, V1) 10.00000 0.000000

VOLUME( WH2, V2) 0.000000 2.000000

VOLUME( WH2, V3) 0.000000 1.000000

VOLUME( WH2, V4) 2.000000 0.000000

VOLUME( WH3, V1) 0.000000 9.000000

VOLUME( WH3, V2) 16.00000 0.000000

VOLUME( WH3, V3) 0.000000 12.00000

VOLUME( WH3, V4) 8.000000 0.000000

Row Slack or Surplus Dual Price

1 400.0000 -1.000000

2 0.000000 0.000000

3 0.000000 -6.000000

4 0.000000 0.000000

5 0.000000 -7.000000

6 0.000000 -6.000000

7 0.000000 -4.000000

8 0.000000 -1.000000

五、解的分析和结论

最小运输费用为400，调运方式为A1到B3，A2到B1，A2到B4，A3到B3，A3到B4。

参考文献：

1. 徐光辉.运筹学基础手册，北京:科学出版社，1999

2. 马振华.现代应用数学手册（运筹学与最优化理论卷）.北京:清华大学出版社，1998

3. lgnizio J P. 目标规划及其应用. 胡运权译. 哈尔滨：哈尔滨工业大学出版社，1988

更多相关推荐：

运筹学课程设计报告(完): 运筹学课程设计报告组别第三组设计人员设计时间20xx年6月25日20xx年7月6日1设计进度本课程设计时间分为两周第一周20xx年6月25日20xx年6月29日建模阶段此阶段各小组根据给出的题目完成模型的建立主...
运筹学课程设计心得: 运筹学课程设计心得每学期的课设都是我们再次收获知识的时刻特别喜欢那种将理论应用到实践中的感觉只有在课设的时候才觉得自己所学是有意义的总是会欣喜的看着自己经过努力而得出的成果只有那一瞬间才会感觉所有的努力和付出都...
运筹学课程设计报告: 长春工业大学课程设计报告课程设计名称运筹课程设计专业班级学生姓名指导教师20xx年7月12日课程设计任务书1运筹学课程设计报告组别第十八组设计人员设计时间20xx年6月27日20xx年7月12日1设计进度本课程...
运筹学课程总结: 运筹学学习总结古人云“运筹帷幄之中，决胜千里之外”，运筹学是20世纪三四十年代发展起来的一门新兴交叉学科，它主要研究人类对各种资源的运用及筹划活动，以期通过了解和发展这种运用及筹划活动的基本规律，发挥有限资源的…
运筹学课程设计报告模板: 宁波大红鹰学院信息工程学院课程设计报告课程名称项目名称姓名班级名称专业名称完成时间运筹学与数据分析实践炼油厂生产计划安排信息管理和信息系统20xx0225信息工程学院一问题的提出正文宋体小四单倍行距这是一个线性...
运筹学课程设计报告: 运筹学课程设计报告求解线性规划问题学校学院专业班级学号姓名MATLAB求解20xx1227空气污染问题某钢厂的钢铁生产对城市的空气造成污染是该城市的主要污染源钢厂主要有两个污染源生产铁的高炉和将生铁炼成钢的平炉...
运筹学课程设计报告: 长春工业大学课程设计报告课程设计名称运筹课程设计专业工商管理班级110508班学生姓名**指导教师**20**年12月20日课程设计任务书运筹学课程设计报告组别：第十二组设计人员：**设计时间：20**.12.…

运筹学课程设计: 长春工业大学课程设计报告Javascript课程设计名称运筹学程序设计专业信息管理与信息系统班级学生姓名指导教师20xx年7月12日运筹学课程设计提纲组别第12组设计人员设计时间20xx年6月29日20xx年7...
运筹学课程设计: 摘要运筹学是一门以人机系统组织管理为对象应用数学计算机等工具来研究各类优先资源的合理规划使用并提供优化决策方案的科学通过对数据的调查收集与统计分析以及具体模型的建立收集和统计上述拟定模型所需要的各种基础数据并最...
运筹学课程设计: 南京工程学院课程设计任务书课程名称运筹学与系统分析课程设计院系部中心专业班级工业工程111姓名丁允想学号20xx10911组员王东磊许燕王尧峄沈鹏飞起止日期20xx1520xx19指导教师邱胜海王志亮1课程设计...
运筹学课程设计: HUNANUNIVERSITY运筹学课程设计报告课程题目整数线性规划及应用学生姓名学生学号专业班级指导老师目录摘要1一整数规划概述21分支定界法32割平面法4301整数规划的数学模型43101规划隐枚举法532...
运筹学课程设计: 运筹学课程设计报告班级工业工程111姓名潘樟兴指导老师范佳静时间目录一模型构造311变量设置312模型构建4121单期模型4122多期模型5二LINDO模型和求解结果621LINDO模型622LINDO求解结果...

热门关注

运筹学课程设计报告书---运输问题的表上作业法

运筹学课程设计

《房屋建筑学》课程设计实训总结