一 集合与函数
1 集合的含义及表示
2
空集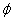 的特殊性: 空集是任何集合的子集,任何非空集合的真子集
的特殊性: 空集是任何集合的子集,任何非空集合的真子集
*结论 含有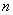 个元素的集合,其子集的个数为
个元素的集合,其子集的个数为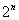 ,真子集的个数为
,真子集的个数为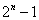
3集合的基本运算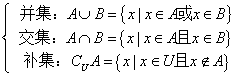
在集合运算中常借助于数轴和文氏图(*注意端点值的取舍)
*结论 (1)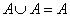
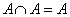 ,
, 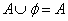
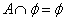
(2)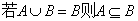
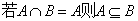
(3)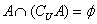
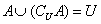
(4)若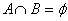 则
则 或
或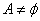
4函数及其表示

5 函数的单调性及应用
(1) 定义: 设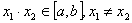 那么:
那么:
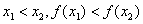
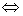
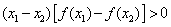
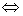

 上是增函数;
上是增函数;
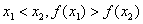
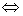
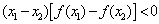
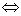
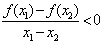
 上是减函数.
上是减函数.
(2) 判定方法: 定义法(证明题)
定义法(证明题)  图像法
图像法  复合法
复合法
(3) 定义法:证明函数单调性用
利用定义来证明函数单调性的一般性步骤:
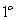 设值:任取
设值:任取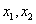 为该区间内的任意两个值,且
为该区间内的任意两个值,且
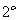 做差,变形,比较大小:做差
做差,变形,比较大小:做差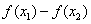 ,并利用通分,因式分解,配方,有理化等方法变形比较
,并利用通分,因式分解,配方,有理化等方法变形比较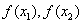 大小
大小
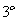 下结论(说函数单调性必须在其单调区间上)
下结论(说函数单调性必须在其单调区间上)
(4)常见函数利用图像直接判断单调性:一次函数,二次函数,反比例函数,指对数函数,幂函数,对勾函数
(5)复合法:针对复合函数采用同增异减原则
(6)单调性中结论:在同一个单调区间内:增+增=增: 增—减=增:减+减=减:减—增=增
若函数 在区间
在区间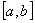 为增函数,则—
为增函数,则— ,
,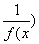 在
在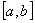 为减函数
为减函数
(7)单调性的应用: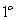 :利用函数单调性比较大小
:利用函数单调性比较大小
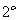 利用函数单调性求函数最值(值域)
利用函数单调性求函数最值(值域)
重点题型:求二次函数在闭区间上的最值问题
6 函数的奇偶性及应用
(1)定义:若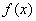 定义域关于原点对称
定义域关于原点对称
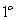 若对于任取x的,均有
若对于任取x的,均有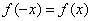 则
则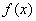 为偶函数
为偶函数
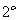 若对于任取x的,均有
若对于任取x的,均有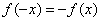 则
则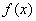 为奇函数
为奇函数
(2)奇偶函数的图像和性质

(3)判定方法: 定义法 (证明题)
定义法 (证明题)  图像法
图像法 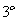 口诀法
口诀法
(4)定义法: 证明函数奇偶性
步骤: 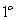 求出函数的定义域观察其是否关于原点对称(前提性必备条件)
求出函数的定义域观察其是否关于原点对称(前提性必备条件)
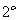 由出发
由出发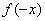 ,寻找其与
,寻找其与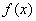 之间的关系
之间的关系
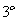 下结论(若
下结论(若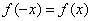 则
则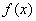 为偶函数,若
为偶函数,若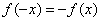 则
则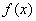 为奇函数函数)
为奇函数函数)
(4) 口诀法: 奇函数+奇函数=奇函数:偶函数+偶函数=偶函数
奇函数 奇函数=偶函数: 奇函数
奇函数=偶函数: 奇函数 偶函数=奇函数:偶函数
偶函数=奇函数:偶函数 偶函数=偶函数
偶函数=偶函数
二 指数函数与对数函数
1 指数运算公式
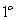
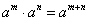
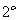
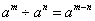
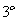
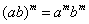
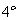

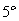
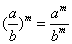

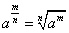
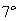
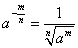
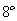
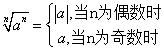
2 对数运算公式
(1)对数恒等式
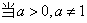 时,
时,
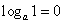

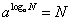
(2)对数的运算法则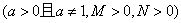
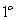
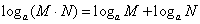
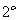
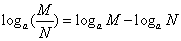
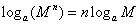
(3)换底公式及推论
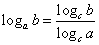
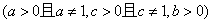
推论 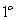
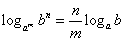
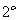
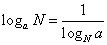
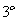
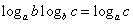
3 指数函数与对数函数

4 指数与对数中的比较大小问题
(1)指数式比较大小
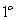
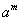 ,
,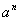
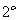
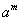 ,
,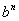
(2)对数式比较大小
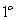
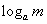 ,
,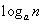
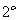
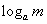 ,
,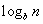
5 指数与对数图像
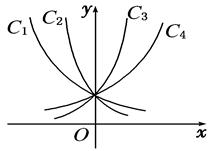
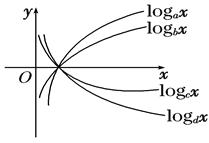
6 幂函数:一般地,函数 叫做幂函数,其
叫做幂函数,其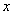 中为自变量,
中为自变量,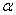 是常数
是常数
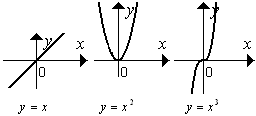
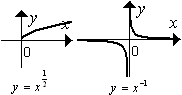
几种幂函数的图象:
函数零点及二分法
一 函数零点的判定
(一) 函数有实数根
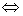 函数的图像与轴有交点
函数的图像与轴有交点
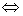 函数有零点
函数有零点
(二) 函数的零点的判定定理
如果函数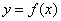 在区间
在区间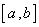 上的图像时连续不断的一条曲线,并且有
上的图像时连续不断的一条曲线,并且有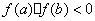 ,那么,函数
,那么,函数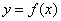 在区间
在区间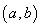 内有零点,即存在
内有零点,即存在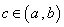 ,使得
,使得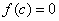 ,这个
,这个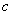 也就是方程的根
也就是方程的根
二 函数二分法的应用
(一)函数二分法:对于在区间上连续不断且的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法。
给定精确度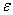 ,用二分法求函数
,用二分法求函数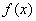 零点近似值的步骤如下:
零点近似值的步骤如下:
1确定区间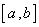 ,验证
,验证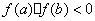 ,给定精确度
,给定精确度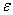
2求区间的中点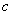
3计算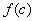
(1) 若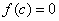 ,则
,则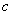 就是函数的零点
就是函数的零点
(2) 若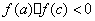 ,则令
,则令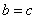 (此时零点
(此时零点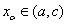 )
)
(3) 若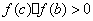 ,则令
,则令 (此时零点
(此时零点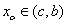 )
)
4判定是否达到精确度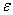 :即若
:即若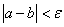 ,则得到零点近似值
,则得到零点近似值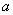 (或
(或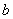 ):否则重复
):否则重复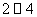
(二)函数二分法及精度计算 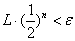
第二篇:高一数学必修一,二知识点总结
高中高一数学必修1各章知识点总结
第一章 集合与函数概念
一、集合有关概念
1、集合的含义:某些指定的对象集在一起就成为一个集合,其中每一个对象叫元素
2、集合的中元素的三个特性:
1.元素的确定性; 2.元素的互异性; 3.元素的无序性
说明:(1)对于一个给定的集合,集合中的元素是确定的,任何一个对象或者是或者不是这个给定的集合的元素。
(2)任何一个给定的集合中,任何两个元素都是不同的对象,相同的对象归入一个集合时,仅算一个元素。
(3)集合中的元素是平等的,没有先后顺序,因此判定两个集合是否一样,仅需比较它们的元素是否一样,不需考查排列顺序是否一样。
(4集合元素的三个特性使集合本身具有了确定性和整体性。
3、集合的表示:{ … } 如{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}
1. 用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}
2.集合的表示方法:列举法与描述法。
注意啊:常用数集及其记法:
非负整数集(即自然数集)记作:N
正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R
关于“属于”的概念
集合的元素通常用小写的拉丁字母表示,如:a是集合A的元素,就说a属于集合A 记作 a∈A ,相反,a不属于集合A 记作 aÏA
列举法:把集合中的元素一一列举出来,然后用一个大括号括上。
描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。用确定的条件表示某些对象是否属于这个集合的方法。
①语言描述法:例:{不是直角三角形的三角形}
②数学式子描述法:例:不等式x-3>2的解集是{xÎR| x-3>2}或{x| x-3>2}
4、集合的分类:
1.有限集 含有有限个元素的集合
2.无限集 含有无限个元素的集合
3.空集 不含任何元素的集合 例:{x|x2=-5}
二、集合间的基本关系
1.“包含”关系—子集
注意: 有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
反之: 集合A不包含于集合B,或集合B不包含集合A,记作A B或B A
2.“相等”关系(5≥5,且5≤5,则5=5)
实例:设 A={x|x2-1=0} B={-1,1} “元素相同”
结论:对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时,集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,即:A=B
① 任何一个集合是它本身的子集。AÍA
②真子集:如果AÍB,且A¹ B那就说集合A是集合B的真子集,记作A B(或B A)
③如果 AÍB, BÍC ,那么 AÍC
④ 如果AÍB 同时 BÍA 那么A=B
3. 不含任何元素的集合叫做空集,记为Φ
规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
三、集合的运算
1.交集的定义:一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.
记作A∩B(读作”A交B”),即A∩B={x|x∈A,且x∈B}.
2、并集的定义:一般地,由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的并集。记作:A∪B(读作”A并B”),即A∪B={x|x∈A,或x∈B}.
3、交集与并集的性质:A∩A = A, A∩φ= φ, A∩B = B∩A,A∪A = A,
A∪φ= A ,A∪B = B∪A.
4、全集与补集
(1)补集:设S是一个集合,A是S的一个子集(即 ),由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集)
记作: CSA 即 CSA ={x | xÎS且 xÏA}
(2)全集:如果集合S含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集。通常用U来表示。
(3)性质:⑴CU(C UA)=A ⑵(C UA)∩A=Φ
二、函数的有关概念
1函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作: y=f(x),x∈A.其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域.
注意:2如果只给出解析式y=f(x),而没有指明它的定义域,则函数的定义域即是指能使这个式子有意义的实数的集合;3 函数的定义域、值域要写成集合或区间的形式.
定义域补充
能使函数式有意义的实数x的集合称为函数的定义域,求函数的定义域时列不等式组的主要依据是:(1)分式的分母不等于零; (2)偶次方根的被开方数不小于零; (3)对数式的真数必须大于零;(4)指数、对数式的底必须大于零且不等于1. (5)如果函数是由一些基本函数通过四则运算结合而成的.那么,它的定义域是使各部分都有意义的x的值组成的集合.(6)指数为零底不可以等于零 (6)实际问题中的函数的定义域还要保证实际问题有意义.
(又注意:求出不等式组的解集即为函数的定义域。)
构成函数的三要素:定义域、对应关系和值域
再注意:(1)构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数)(2)两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。相同函数的判断方法:①表达式相同;②定义域一致 (两点必须同时具备)
(见课本21页相关例2)
值域补充
(1)、函数的值域取决于定义域和对应法则,不论采取什么方法求函数的值域都应先考虑其定义域. (2).应熟悉掌握一次函数、二次函数、指数、对数函数及各三角函数的值域,它是求解复杂函数值域的基础。
3. 函数图象知识归纳
(1)定义:在平面直角坐标系中,以函数 y=f(x) , (x∈A)中的x为横坐标,函数值y为纵坐标的点P(x,y)的集合C,叫做函数 y=f(x),(x ∈A)的图象.
C上每一点的坐标(x,y)均满足函数关系y=f(x),反过来,以满足y=f(x)的每一组有序实数对x、y为坐标的点(x,y),均在C上 . 即记为C={ P(x,y) | y= f(x) , x∈A }
图象C一般的是一条光滑的连续曲线(或直线),也可能是由与任意平行与Y轴的直线最多只有一个交点的若干条曲线或离散点组成。
(2) 画法
A、描点法:根据函数解析式和定义域,求出x,y的一些对应值并列表,以(x,y)为坐标在坐标系内描出相应的点P(x, y),最后用平滑的曲线将这些点连接起来.
B、图象变换法(请参考必修4三角函数)
常用变换方法有三种,即平移变换、伸缩变换和对称变
(3)作用:
1、直观的看出函数的性质;2、利用数形结合的方法分析解题的思路。提高解题的速度。发现解题中的错误。
4.快去了解区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;(2)无穷区间;(3)区间的数轴表示.
5.什么叫做映射
一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A B为从集合A到集合B的一个映像。记作“f:A B”
给定一个集合A到B的映像,如果a∈A,b∈B.且元素a和元素b对应,那么,我们把元素b叫做元素a的象,元素a叫做元素b的原象
说明:函数是一种特殊的映射,映射是一种特殊的对应,①集合A、B及对应法则f是确定的;②对应法则有“方向性”,即强调从集合A到集合B的对应,它与从B到A的对应关系一般是不同的;③对于映射f:A→B来说,则应满足:(Ⅰ)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(Ⅱ)集合A中不同的元素,在集合B中对应的象可以是同一个;(Ⅲ)不要求集合B中的每一个元素在集合A中都有原象。
常用的函数表示法及各自的优点:
1 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;2 解析法:必须注明函数的定义域;3 图象法:描点法作图要注意:确定函数的定义域;化简函数的解析式;观察函数的特征;4 列表法:选取的自变量要有代表性,应能反映定义域的特征.
注意啊:解析法:便于算出函数值。列表法:便于查出函数值。图象法:便于量出函数值
补充一:分段函数 (参见课本P24-25)
在定义域的不同部分上有不同的解析表达式的函数。在不同的范围里求函数值时必须把自变量代入相应的表达式。分段函数的解析式不能写成几个不同的方程,而就写函数值几种不同的表达式并用一个左大括号括起来,并分别注明各部分的自变量的取值情况.(1)分段函数是一个函数,不要把它误认为是几个函数;(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
补充二:复合函数
如果y=f(u),(u∈M),u=g(x),(x∈A),则 y=f[g(x)]=F(x),(x∈A) 称为f、g的复合函数。
例如: y=2sinX y=2cos(X2+1)
7.函数单调性
(1).增函数
设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在区间D上是增函数。区间D称为y=f(x)的单调增区间(睇清楚课本单调区间的概念)
如果对于区间D上的任意两个自变量的值x1,x2,当x1<x2 时,都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数.区间D称为y=f(x)的单调减区间.
注意:1 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
2 必须是对于区间D内的任意两个自变量x1,x2;当x1<x2时,总有f(x1)<f(x2) 。
(2) 图象的特点
如果函数y=f(x)在某个区间是增函数或减函数,那么说函数y=f(x)在这一区间上具有(严格的)单调性,在单调区间上增函数的图象从左到右是上升的,减函数的图象从左到右是下降的.
(3).函数单调区间与单调性的判定方法
(A) 定义法:
1 任取x1,x2∈D,且x1<x2;2 作差f(x1)-f(x2);3 变形(通常是因式分解和配方);4 定号(即判断差f(x1)-f(x2)的正负);5 下结论(指出函数f(x)在给定的区间D上的单调性).
(B)图象法(从图象上看升降)_
(C)复合函数的单调性
函数的单调性
注意:1、函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集. 2、还记得我们在选修里学习简单易行的导数法判定单调性吗?
8.函数的奇偶性
(1)偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
(2).奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数.
注意:1 函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;函数可能没有奇偶性,也可能既是奇函数又是偶函数。
2 由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
(3)具有奇偶性的函数的图象的特征
偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
总结:利用定义判断函数奇偶性的格式步骤:1 首先确定函数的定义域,并判断其定义域是否关于原点对称;2 确定f(-x)与f(x)的关系;3 作出相应结论:若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数.
注意啊:函数定义域关于原点对称是函数具有奇偶性的必要条件.首先看函数的定义域是否关于原点对称,若不对称则函数是非奇非偶函数.若对称,(1)再根据定义判定; (2)有时判定f(-x)=±f(x)比较困难,可考虑根据是否有f(-x)±f(x)=0或f(x)/f(-x)=±1来判定; (3)利用定理,或借助函数的图象判定 .
9、函数的解析表达式
(1).函数的解析式是函数的一种表示方法,要求两个变量之间的函数关系时,一是要求出它们之间的对应法则,二是要求出函数的定义域.
(2).求函数的解析式的主要方法有:待定系数法、换元法、消参法等,如果已知函数解析式的构造时,可用待定系数法;已知复合函数f[g(x)]的表达式时,可用换元法,这时要注意元的取值范围;当已知表达式较简单时,也可用凑配法;若已知抽象函数表达式,则常用解方程组消参的方法求出f(x)
10.函数最大(小)值(定义见课本p36页)
1 利用二次函数的性质(配方法)求函数的最大(小)值2 利用图象求函数的最大(小)值3 利用函数单调性的判断函数的最大(小)值:如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减则函数y=f(x)在x=b处有最大值f(b);如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b);
第二章 基本初等函数
一、指数函数
(一)指数与指数幂的运算
1.根式的概念:一般地,如果 ,那么 叫做 的 次方根(n th root),其中 >1,且 ∈ *.
当 是奇数时,正数的 次方根是一个正数,负数的 次方根是一个负数.此时, 的 次方根用符号 表示.式子 叫做根式(radical),这里 叫做根指数(radical exponent), 叫做被开方数(radicand)
当 是偶数时,正数的 次方根有两个,这两个数互为相反数.此时,正数 的正的 次方根用符号 表示,负的 次方根用符号- 表示.正的 次方根与负的 次方根可以合并成± ( >0).由此可得:负数没有偶次方根;0的任何次方根都是0,记作 。
注意:当 是奇数时, ,当 是偶数时,
2.分数指数幂
正数的分数指数幂的意义,规定:
0的正分数指数幂等于0,0的负分数指数幂没有意义
指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.
(二)指数函数及其性质
1、指数函数的概念:一般地,函数 叫做指数函数(exponential ),其中x是自变量,函数的定义域为R.
注意:指数函数的底数的取值范围,底数不能是负数、零和1.
图象特征
函数性质
1.向x、y轴正负方向无限延伸
函数的定义域为R
2.图象关于原点和y轴不对称
非奇非偶函数
3.函数图象都在x轴上方
4.函数的值域为R+
5.函数图象都过定点(0,1)
6.自左向右看图象逐渐上升自左向右看,图象逐渐下降
图象上升趋势是越来越陡
图象上升趋势是越来越缓
函数值开始增长较慢,到了某一值后增长速度极快;
函数值开始减小极快,到了某一值后减小速度较慢;
注意:利用函数的单调性,结合图象还可以看出:
(1)在[a,b]上, 值域是 或 ;
(2)若 ,则 ; 取遍所有正数当且仅当 ;
(3)对于指数函数 ,总有 ;
(4)当 时,若 ,则 ;
二、对数函数
(一)对数
1.对数的概念:一般地,如果 ,那么数 叫做以 为底 的对数,记作: ( — 底数, — 真数, — 对数式)
两个重要对数:
1 常用对数:以10为底的对数 ;
2 自然对数:以无理数 为底的对数的对数 .
(二)对数函数
1、对数函数的概念:函数 ,且 叫做对数函数,其中 是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。
图象特征,函数性质
1.函数图象都在y轴右侧
函数的定义域为(0,+∞)
2.图象关于原点和y轴不对称
非奇非偶函数
3.向y轴正负方向无限延伸
函数的值域为R
4.函数图象都过定点(1,0)
自左向右看,图象逐渐上升,自左向右看,图象逐渐下降
(三)幂函数
1、幂函数定义:一般地,形如 的函数称为幂函数,其中 为常数.
2、幂函数性质归纳.
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
(2) 时,幂函数的图象通过原点,并且在区间 上是增函数.特别地,当 时,幂函数的图象下凸;当 时,幂函数的图象上凸;
(3) 时,幂函数的图象在区间 上是减函数.在第一象限内,当 从右边趋向原点时,图象在 轴右方无限地逼近 轴正半轴,当 趋于 时,图象在 轴上方无限地逼近 轴正半轴.
第三章 函数的应用
、方程的根与函数的零点
1、函数零点的概念:对于函数 ,把使 成立的实数 叫做函数 的零点。
2、函数零点的意义:函数 的零点就是方程 实数根,亦即函数 的图象与 轴交点的横坐标。即:
方程 有实数根 函数 的图象与 轴有交点 函数 有零点.
3、函数零点的求法:
求函数 的零点:
1 (代数法)求方程 的实数根;
2 (几何法)对于不能用求根公式的方程,可以将它与函数 的图象联系起来,并利用函数的性质找出零点.
4、二次函数的零点:
二次函数 .
1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点.
2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点.
高一数学必修4
3)△<0,方程 无
2、角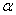 的顶点与原点重合,角的始边与
的顶点与原点重合,角的始边与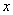 轴的非负半轴重合,终边落在第几象限,则称
轴的非负半轴重合,终边落在第几象限,则称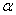 为第几象限角.
为第几象限角.
第一象限角的集合为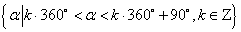
第二象限角的集合为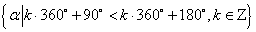
第三象限角的集合为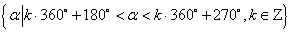
第四象限角的集合为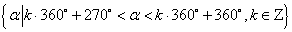
终边在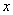 轴上的角的集合为
轴上的角的集合为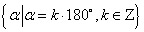
终边在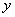 轴上的角的集合为
轴上的角的集合为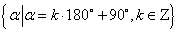
终边在坐标轴上的角的集合为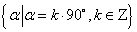
3、与角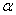 终边相同的角的集合为
终边相同的角的集合为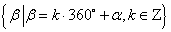
4、已知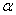 是第几象限角,确定
是第几象限角,确定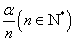 所在象限的方法:先把各象限均分
所在象限的方法:先把各象限均分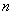 等份,再从
等份,再从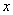 轴的正半轴的上方起,依次将各区域标上一、二、三、四,则
轴的正半轴的上方起,依次将各区域标上一、二、三、四,则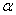 原来是第几象限对应的标号即为
原来是第几象限对应的标号即为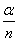 终边所落在的区域.
终边所落在的区域.
5、长度等于半径长的弧所对的圆心角叫做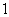 弧度.
弧度.
6、半径为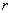 的圆的圆心角
的圆的圆心角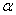 所对弧的长为
所对弧的长为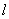 ,则角
,则角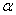 的弧度数的绝对值是
的弧度数的绝对值是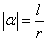 .
.
7、弧度制与角度制的换算公式: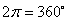 ,
,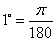 ,
,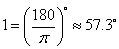 .
.
8、若扇形的圆心角为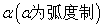 ,半径为
,半径为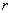 ,弧长为
,弧长为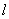 ,周长为
,周长为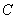 ,面积为
,面积为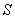 ,则
,则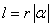 ,
,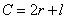 ,
,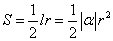 .
.
9、设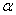 是一个任意大小的角,
是一个任意大小的角,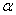 的终边上任意一点
的终边上任意一点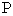 的坐标是
的坐标是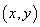 ,它与原点的距离是
,它与原点的距离是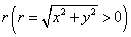 ,则
,则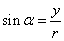 ,
,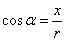 ,
,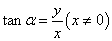 .
.
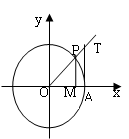 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正.
10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正.
11、三角函数线: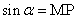 ,
,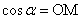 ,
,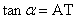 .
.
12、同角三角函数的基本关系: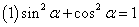
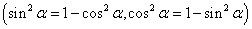 ;
;
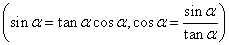 .
.
13、三角函数的诱导公式:
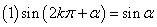 ,
,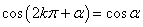 ,
,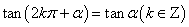 .
.
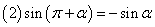 ,
,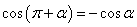 ,
,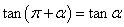 .
.
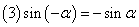 ,
,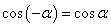 ,
,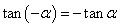 .
.
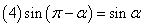 ,
,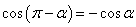 ,
,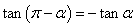 .
.
口诀:函数名称不变,符号看象限.
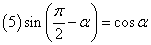 ,
,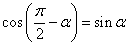 .
.
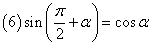 ,
,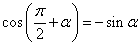 .
.
口诀:奇变偶不变,符号看象限.
14、函数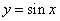 的图象上所有点向左(右)平移
的图象上所有点向左(右)平移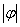 个单位长度,得到函数
个单位长度,得到函数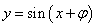 的图象;再将函数
的图象;再将函数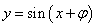 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的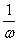 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数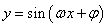 的图象;再将函数
的图象;再将函数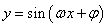 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的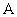 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数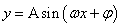 的图象.
的图象.
函数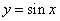 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的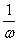 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数
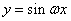 的图象;再将函数
的图象;再将函数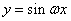 的图象上所有点向左(右)平移
的图象上所有点向左(右)平移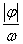 个单位长度,得到函数
个单位长度,得到函数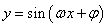 的图象;再将函数
的图象;再将函数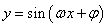 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的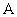 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数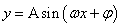 的图象.
的图象.
函数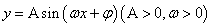 的性质:
的性质:
①振幅: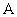 ;②周期:
;②周期: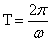 ;③频率:
;③频率: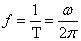 ;④相位:
;④相位: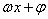 ;⑤初相:
;⑤初相: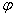 .
.
函数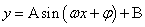 ,当
,当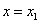 时,取得最小值为
时,取得最小值为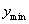 ;当
;当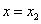 时,取得最大值为
时,取得最大值为 ,则
,则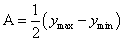 ,
,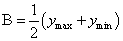 ,
,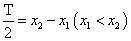 .
.
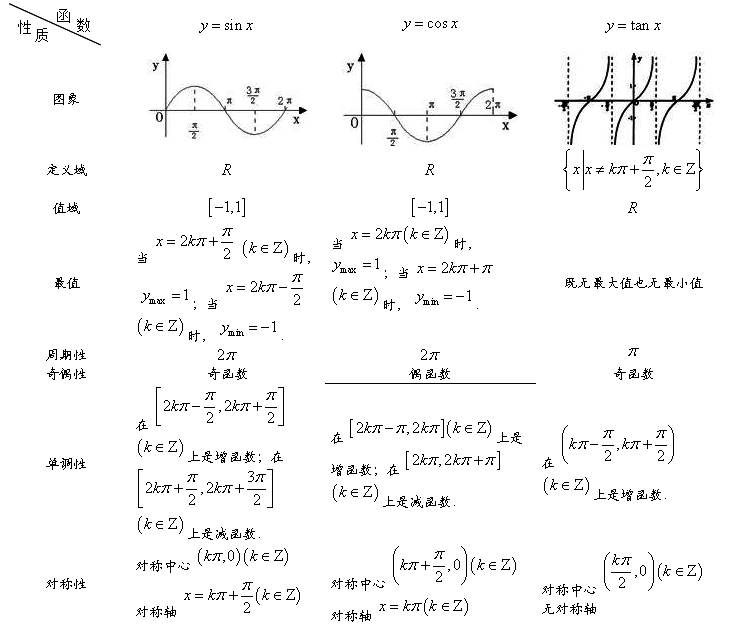
15、正弦函数、余弦函数和正切函数的图象与性质:
16、向量:既有大小,又有方向的量.
数量:只有大小,没有方向的量.
有向线段的三要素:起点、方向、长度.
零向量:长度为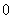 的向量.
的向量.
单位向量:长度等于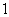 个单位的向量.
个单位的向量.
平行向量(共线向量):方向相同或相反的非零向量.零向量与任一向量平行.
 相等向量:长度相等且方向相同的向量.
相等向量:长度相等且方向相同的向量.
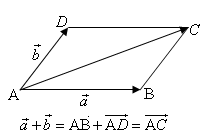
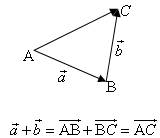
17、向量加法运算:
⑴三角形法则的特点:首尾相连.
⑵平行四边形法则的特点:共起点.
⑶三角形不等式: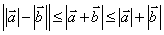 .
.
 ⑷运算性质:①交换律:
⑷运算性质:①交换律: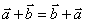 ;②结合律:
;②结合律: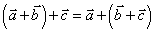 ;③
;③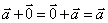 .
.
⑸坐标运算:设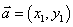 ,
,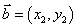 ,则
,则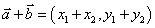 .
.
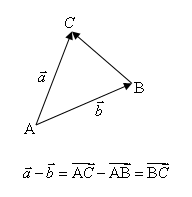
18、向量减法运算:
⑴三角形法则的特点:共起点,连终点,方向指向被减向量.
⑵坐标运算:设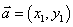 ,
,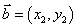 ,则
,则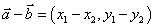 .
.
设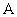 、
、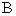 两点的坐标分别为
两点的坐标分别为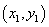 ,
,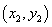 ,则
,则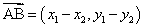 .
.
19、向量数乘运算:
⑴实数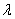 与向量
与向量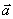 的积是一个向量的运算叫做向量的数乘,记作
的积是一个向量的运算叫做向量的数乘,记作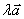 .
.
①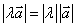 ;
;
②当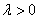 时,
时,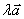 的方向与
的方向与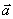 的方向相同;当
的方向相同;当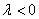 时,
时,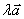 的方向与
的方向与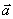 的方向相反;当
的方向相反;当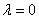 时,
时,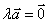 .
.
⑵运算律:①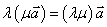 ;②
;②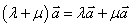 ;③
;③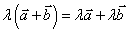 .
.
⑶坐标运算:设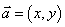 ,则
,则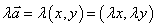 .
.
20、向量共线定理:向量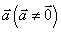 与
与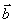 共线,当且仅当有唯一一个实数
共线,当且仅当有唯一一个实数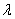 ,使
,使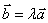 .
.
设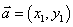 ,
,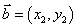 ,其中
,其中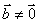 ,则当且仅当
,则当且仅当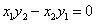 时,向量
时,向量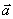 、
、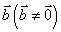 共线.
共线.
21、平面向量基本定理:如果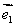 、
、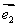 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量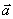 ,有且只有一对实数
,有且只有一对实数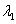 、
、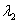 ,使
,使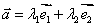 .(不共线的向量
.(不共线的向量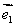 、
、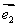 作为这一平面内所有向量的一组基底)
作为这一平面内所有向量的一组基底)
22、分点坐标公式:设点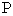 是线段
是线段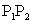 上的一点,
上的一点,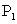 、
、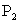 的坐标分别是
的坐标分别是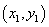 ,
,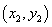 ,当
,当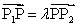 时,点
时,点 的坐标是
的坐标是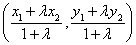 .
.
23、平面向量的数量积:
⑴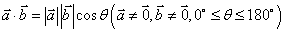 .零向量与任一向量的数量积为
.零向量与任一向量的数量积为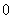 .
.
⑵性质:设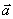 和
和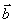 都是非零向量,则①
都是非零向量,则①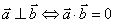 .②当
.②当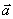 与
与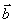 同向时,
同向时,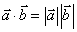 ;当
;当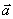 与
与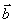 反向时,
反向时,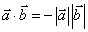 ;
;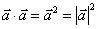 或
或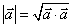 .③
.③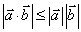 .
.
⑶运算律:①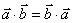 ;②
;②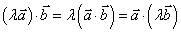 ;③
;③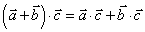 .
.
⑷坐标运算:设两个非零向量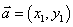 ,
,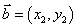 ,则
,则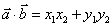 .
.
若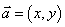 ,则
,则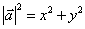 ,或
,或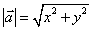 .
.
设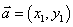 ,
,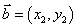 ,则
,则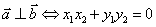 .
.
设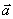 、
、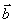 都是非零向量,
都是非零向量,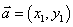 ,
,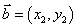 ,
,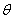 是
是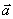 与
与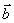 的夹角,则
的夹角,则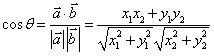 .
.
24、两角和与差的正弦、余弦和正切公式:
⑴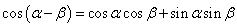 ;
;
⑵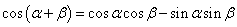 ;
;
⑶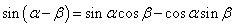 ;
;
⑷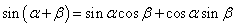 ;
;
⑸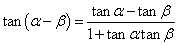 (
(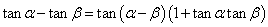 );
);
⑹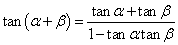 (
(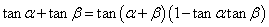 ).
).
25、二倍角的正弦、余弦和正切公式:
⑴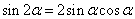 .
.
⑵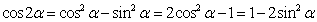 (
(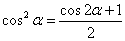 ,
,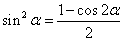 ).
).
⑶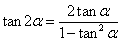 .
.
26、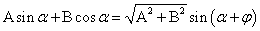 ,其中
,其中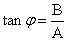 .
.
www.ks5u.com
实根,二次函数的图象与 轴无交点,二次函数无零点.
