All Of Me 予我所有 [Verse 1:]第一节： What would I do without your smart mouth 没有你伶牙俐齿我怎么办吶 Drawing me in, and you kicking me out 轻易的收我进来，又踹了我出去 Got my head spinning, no kidding, I can't pin you down 让我晕头转向，不是开玩笑，我真的无法定住你 What's going on in that beautiful mind 你美丽的思维里到底在考虑着什么 I'm on your magical mystery ride 我在你魔法秘境里兜兜转转 And I'm so dizzy, don't know what hit me, but I'll be alright 我还眩晕着，不知道什么击中了我，不过我想这没什么关系 [Bridge:]衔接： My head's under water But I'm breathing fine You're crazy and I'm out of my mind [Chorus:]合音： 'Cause all of me 因为所有的我 Loves all of you 都爱所有的你 Love your curves and all your edges 沉浸于你所有的曲线和背影 All your perfect imperfections 所有你完美的不完美 Give your all to me 把你的所有都交给我 I'll give my all to you 我把所有的自己都交给你 You're my end and my beginning 你是我的终点和我的起点 Even when I lose I'm winning 无论我的输赢 1 / 3

'Cause I give you all of me 因为我给了你所有的自己 And you give me all, all of you, oh 你给了我所有的你 [Verse 2:]第二节 How many times do I have to tell you 不知告诉你了多少次 Even when you're crying you're beautiful too 即便你在哭喊，你也是那么美丽 The world is beating you down, I'm around through every mood 无论这个世界负你几何，我都陪你一起度过 You're my downfall, you're my muse 你是我的奔涌而下的瀑布，你是我的缪斯 My worst distraction, my rhythm and blues 你拨乱了我每根神经，我所有的旋律和忧愁 I can't stop singing, it's ringing, in my head for you 我的歌声停不下来，它在召唤我，在我的脑海里为你召唤着我 [Bridge:] My head's under water 仿佛坠入水中 But I'm breathing fine 我还照常呼吸着 You're crazy and I'm out of my mind 你真是疯狂，我也只好陪你一起 [Chorus:]合音： 'Cause all of me 因为所有的我 Loves all of you 都爱所有的你 Love your curves and all your edges 沉浸于你所有的曲线和背影 All your perfect imperfections 所有你完美的不完美 Give your all to me 把你的所有都交给我 I'll give my all to you 2 / 3

我把所有的自己都交给你 You're my end and my beginning 你是我的终点和我的起点 Even when I lose I'm winning 无论我的输赢 'Cause I give you all of me 因为我给了你所有的自己 And you give me all, all of you, oh 你给了我所有的你 Give me all of you 把你自己交给我 Cards on the table, we're both showing hearts 知根知底，心有灵犀 Risking it all, though it's hard 赌上所有，即便它那么难下决心 [Chorus:]合音： 'Cause all of me 因为所有的我 Loves all of you 都爱所有的你 Love your curves and all your edges 沉浸于你所有的曲线和背影 All your perfect imperfections 所有你完美的不完美 Give your all to me 把你的所有都交给我 I'll give my all to you 我把所有的自己都交给你 You're my end and my beginning 你是我的终点和我的起点 Even when I lose I'm winning 无论我的输赢 'Cause I give you all of me 因为我给了你所有的自己 And you give me all, all of you, oh 你给了我所有的你 3 / 3

第二篇：电子商务英文阅读材料

Auctioningsupplycontractswithuncertaindemand

CuihongLi

GraduateSchoolofIndustrialAdministration

CarnegieMellonUniversity

5000ForbesAvenue

Pittsburgh,PA15213

cuihong@andrew.cmu.edu

AlanScheller-Wolf

GraduateSchoolofIndustrialAdministration

CarnegieMellonUniversity

5000ForbesAvenue

awolf@andrew.cmu.eduAnupriyaAnkolekarSchoolofComputerScienceCarnegieMellonUniverity5000ForbesAvenuePittsburgh,PA15213anupriya@cs.cmu.eduKatiaSycaraRoboticsInstituteCarnegieMellonUniversity5000ForbesAvenuePittsburgh,PA15213

katia@cs.cmu.edu

Abstract

Designofthecontractform,togetherwiththenegotiationmechanismandstrategy,comprisethecoredecisionsinane-contractingprocess.Inabusiness-to-businessscenarioabuyer(e.g.,aretailer)usuallyneedstosignacontractwithasupplier(e.g.,aman-ufacturer)tosatisfyademandthatisuncertainatthetimeofcontracting.Thebuyerwouldliketohaveordering?exibilitytorespondtotheuncertaindemandrealization.Butthesupplythatcanbeprovidedmaybeconstrainedbythecapacityinvestmentofthesupplier,whichhastobemadeinadvance.Thecapacityofasuppliermayei-therbeobservableandhencecontractable,orunobservableandhencenotenforcablebyacontract.Weproposetwocontractforms,anoptioncontractforthesituationwithobservablecapacity,andawholesalepricecontractwithafranchisefee(WF)forthesituationwithunobservablecapacity.Inbothcontractsthebuyerplacesher?nalorderafterthedemandisknown.Inanoptioncontractthebuyer?rstpaysapremiumfeeforreservingacertaincapacityfromthesupplierinadvance,andthenanexercisefeeforeachunitthatisordered.InaWFcontractthesupplierchargesawholesalepriceforeachunitorderedbythebuyer,butpaysa?xedfranchisefeetothebuyer.Wepresentoptimalauctionmechanismsindi?erentprotocolsforthebuyertonegotiateanoptioncontractoraWFcontractwithcompetingsuppliers.Bothcontractsgeneratehigherutil-ityforthebuyerthanthecontractinwhichthebuyerprocuresinadvance.Ourresultsshowthattheoptimalauctionsforthesetwocontractshavethesameoutcome.Wealsodiscusstheimplementationofe-contractingbasedonourcontractauctionmechanismswithsoftwareagenttechnologies.

1

1Introduction

Therapiddevelopmentofcomputerandcommunicationtechnologieshasacceleratedthebusinessprocessesfromlaborservicestoelectronic(semi-)automatedprocesses[13].Con-tractingisoneoftheimportantbusinessprocessesthathasrecentlyreceivedmuchattentioninthistrendtowardelectronictransactions.E-contractingaimstoautomatetheprocessofcreating,negotiating,closingandmonitoringtheperformanceofcontracts[2].Theproperdesignofthecontract,andthenegotiationmechanismandstrategy,dependsonthespeci?cbusinesssituation,andisthecoreofthedecisionsinthee-contractingprocess.

Contractinginabusiness-to-consumer(B2C)andinabusiness-to-business(B2B)scenarioaredi?erent.InaB2Cscenario,forexampleoftheauctionsoneBay,theitemstoexchangeareprede?nedinthequantityandotherattributes.Acontractusuallyonlyneedstospecifyaone-shotexchangecondition,forexample,theprice.Astandardcontractformcanthusexist,andthenegotiationissimple,becausetherearefewattributes,usuallyonlytheprice,tonegotiate.Butinabusiness-to-business(B2B)worldthecontractingpartiesareusuallyinvolvedinarelationshipoveranextendedhorizon.Theservice/goodtonegotiateandcontractmaybecon?gurable,andhencethecontractcanbehighlyunstructuredandinvolvemanyattributes,suchastheprice,deliverytime,quantity,etc.ThisnegotiationismorecomplicatedthaninaB2Cscenariobecausemultipleattributesareinvolved,andsometimeseventhecontractformcanbeanobjectofnegotiation.Moreover,thegoalofB2Bcontractingisnotonlytoensureaproperdivisionofpro?ts,butalsotocreatemorepro?t,bycoordinatingandenforcingthebehaviorsofbothparties.DesignofthecontractformandnegotiationmechanismisthusespeciallyimportantinaB2Bscenario,toachievecoordinationandane?cientwin-winsituationforbothparties.

Considerabuyer(retailer)thatwantstosignacontractwithasupplier(manufacturer)tosatisfythedemandinacomingsellingseason.Thebuyermaynotknowtheexactdemandintheseasonwhenshesignsthecontract,asshehastocontractwithasupplierwellinadvancesothatthelatterpartycanprepare,forexample,byprocuringcomponentsandrawmaterialsfromherupstreamsupplier.Thiscapacityset-upmayrequirelongleadtime,leavingnoopportunityforthesuppliertoexpandthecapacityduringtheseason:thecapacityinvestmentofthesupplierconstrainsthesupply.Butwhilethesupplierdoesnotwanttowastemoneyonexcesscapacity,thebuyerdoesnotwantcapacityshortages.Toensureagooddemandsatisfactionlevelthebuyerthushastoprovideincentivesforthesuppliertoinvestinsu?cientcapacity.Therearedi?erentwaystoprovidethisincentive.Onestraightforwardwayisforthebuyerto?xthequantitythatsheisgoingtobuy.Thisisequivalenttomakingadvancedprocurement,leavingnoordering?exibilitytocounterthedemanduncertainty.Anotherwaytoprovideincentivesforcapacityinvestment,whileretainingordering?exibility,istocompletetheprocurementintwostages.Inthe?rststagethebuyerreservescapacityandinthesecondstagethebuyerpurchasestheproductbasedontherealizeddemand.Thisprocesscanberegulatedbyanoptioncontract.Withanoptioncontractthebuyerpaysthesupplierapremiumfeefortherighttobuyacertainamountoftheproduct.Afterthe

2

demandisobserved,thebuyercanplaceordersfortheproductinanamountuptothenumberofoptions,payinganexercisefeeforeachunitthatisordered.Anoptioncontractallowsrisksharing,andhenceinducesbettercoordination,creatingawin-winsituationbetweentheparties.Thebuyerwillordermoreonaveragethanshewouldunderacontractinwhichshehastoperformalltheprocurementbeforethedemandisknown,andthesupplierwillinvestmoreincapacitythanshewouldwithoutcontractinguponcapacityreservation.

Withanoptioncontractthebuyermustbeabletoobserveandverifythecapacitypreparedbythesupplier.Ifthecapacityisnotobservable,thecapacityreservationcannotregulatethecapacityinvestmentofthesupplier.Inthissituationtheincentiveforcapacityinvestmentonlyreliesontheexercisefee,whichisequivalenttoawholesaleprice.Inthiscasepayingapremiumfeemakesnosense,insteadafranchisefee,paidbythesupplier,thatisindependentoftheorderedquantitycanensurebetterpro?tdistributionbetweenthetwoparties.Wecallthiscontractawholesalepricecontractwithafranchisefee(WF).

Typicallyabuyerdoesnotknowthee?ciency,ortheproductioncost,ofasupplier.Whenseveralsuppliersarepossiblecandidatestoprovidetheproduct,competitivebiddingisane?cientmechanismforthebuyertodiscoverthemostcompetentsupplierandnegotiateacontract.Thismaytakeplaceinamulti-attributeauctionthatinvolvesallthenegotiabletermsinthecontract,forexamplethepremiumfee,exercisefeeandcapacityinanoptioncontract,andthewholesalepriceandthefranchisefeeinaWFcontract.Therearetwomainclassesofprotocolsforsuchmulti-attributeauctions:The?rstclassisauctionswithamenuofcontracts,andthesecondclassisauctionswithascoringrule.Inthe?rstclasstheauctioneer,thebuyer,announcesasetofcontractalongwiththepreferenceorderbetweenthecontracts.Thesuppliersbidbychoosingacontract,andtheonewhobidsthehighestrankedcontractisthewinner.Inthesecondclasstheauctioneerannouncesascoringfunction.Thesuppliersbidbysubmittingcontracts,andthewinnerisdecidedbythescoringrule.

Inthispaperwepresentoptimalauctionmechanismsindi?erentprotocolsforbothanoptioncontractandaWFcontract,whenthecostofasupplierisunknowntothebuyer.Wealsodiscusstheimplementationandautomationofthecontractauctionmechanismswithsoftwareagenttechnologies.Althoughonewouldexpectthebuyertolosecertainadvantageswhenasupplier’scapacityisunobservable,surprisinglyweshowthatbyappropriatelydesigningthecontractformandauctionmechanism,thebuyercanactuallyachievethesameoptimalexpectedutilitywithunobservablecapacityaswithobservablecapacity.Inbothsituations,theordering?exibilityinanoptioncontractoraWFcontractresultsinhigherutilityforthebuyerthanpre-specifyinga?xedorderingquantity.

Therestofthepaperisorganizedasfollows:WereviewtherelatedworkinSection2.Section3setsuptheproblem,andprovidestheframeworkforauctionmechanismdesign.WepresenttheoptimalauctionmechanismsforanoptioncontractinSection4,andforaWFcontractinSection5.TheimplementationandautomationofthesupplycontractauctionswithsoftwareagentsisdiscussedinSection6.

3

2Relatedwork

Insupplychainmanagementdesignofcontractshasbeenanactivesubjectaimedatreconcil-ingcon?ictsandachievebettercoordinationbetweenparties:[3]providesagoodintroductionandsurveyonthiswork.Itprovidestheanalysisoftheoptimaloptioncontractandwholesalepricecontract(withoutafranchisefee)betweenabuyerandasupplierwhenthedemandforecastisprivateinformationofthebuyer,butthecostofthesupplierisknownbythebuyer.Thewholesalepricecontractresultsinlesspro?tforthebuyerwhencapacityisun-observable,ascomparedtotheoptioncontractwhencapacityisobservable.Inourpaperwestudyauctionsforsupplycontractswhentherearemultiplecompetingsuppliersandthecostsofsuppliersareunknown.Thewholesalepricecontract,byintroducingafranchisefee,actuallyresultsinthesameoptimaloutcomeasanoptioncontract.Anotherrelatedwork,

[7],investigatestheroleofoptionsinabuyer-suppliersystem,illustratinghowtheyprovide?exibilityandachievechannelcoordination.Thatworkisbasedoncompleteinformation-eachpartyknowstheother’scostorrevenue.

Auctionshavebeenconsideredinprocurementtodiscoverthemostcompetentsupplier,thuscuttingcost.Theauctionmechanismforabuyertoprocurefromoneofmultiplecompetingsuppliersisstudiedin[6]and[5].Theitemtoauctionisasupplycontractwithtwoattributes:theproductquantityandpayment.Inourpaperwestudytheauctiondesignforasupplycontractinwhichtheorderingquantityisnotspeci?edbutdeterminedafterwards,basedontherealizeddemand.Undersuchdemanduncertaintythebuyerachieveshigherpro?twithanoptioncontractoraWFcontractthaninacontractwithapre-speci?edquantity.Indirectmulti-attributeauctionmechanismsarestudiedin[4],whichproposesascoringrulebasedonwhich?rst-scoreandsecond-scoresealed-bidauctionsimplementtheoptimalauctionmechanism.Thetwoattributesinthispaperarethepriceandquality(whichcanalsobeinterpretedasthequantity).Thedesignofthescoringruleinourpaperisinspiredby[4],butourauctionsarebasedondi?erentcontracts,usinganEnglishauctionprotocol.Englishauctiondesignformulti-attributeitemsisconsideredin[9,8,10].Theutilityfunctionofthebuyerandthescoringrulearebothlinearfunctionsoftheattributes.Basedonthislinearfunctionalformtheoptimalweightsoftheattributesinthescoringruleareproposed,andthestrategiesofthebiddersareanalyzed.ThemechanismisonlyoptimalamongEnglishauctionswithlinearscoringfunctions,notwithgeneralscoringfunctionsasweallow.

Inrecentyearstherehasbeengrowingresearchinterestindesigningandimplementingau-tomatedelectronictradingsystemswithsoftwareagents.TheTradingAgentCompetition(TAC)inSupplyChainManagement[1]promotesandencouragesthedevelopmentofintelli-gentsoftwareagentscapableofbuyingorsellingproducts/materialsonbehalfofacompany.ThecompetitionisbasedonaB2Bsituation,andtheinternaloperationsofthecompaniesareintegratedintobiddingdecisions[17].Theseexchangesarebasedonaone-shotrela-tionship:thecontractsspecifytheorderingquantitiesandleavenopurchasing?exibilitytocounterdemanduncertainty.Finally,[20]studiesauctionmechanismdesignforsupplychainformationtoachieveglobale?ciency.Againtheauctionsarebasedonknowndemand.

4

3De?nitionofthemodel

Inthissectionweshall?rstdescribethenotationsandtheproblemsetting,thenintroducetheauctionmechanismdesignframework.Thebuyerhasuncertaindemanddofaproductˉ(·)=1?H(·)withprobabilitydistributionanddensityfunctionsG(d)andg(d).De?neH

forageneralprobabilitydistributionfunctionH(·).Thebuyersourcestheproductfromasupplierwithasupplycontract.Thelead-timeforproductioniszero.Butbeforeproduction(andaftercontracting)thesupplierhastoinvestincapacity,whichconstrainstheamountofsupply.Whenthecapacityisx,theexpectedsatis?eddemandisS(x),whereS(x)=ˉ(x).Ex[min{d,x}]=x?E[(x?d)+]withthederivativeS??(x)=G

Thebuyersellstheproducttoconsumersata?xedmarketpricerthatisexogenouslygiven.Therearensupplierswhocompeteforthesupplycontract.Eachsupplier’scostfunctioniscomposedoftwoparts:thecapacityinvestmentcostandtheproductioncost.Foreachunitofcapacity,whichproducesoneproduct,thecostkis?xedandidenticalforallsuppliers.Thecostisknownbythebuyerandthesuppliers.Theunitproduction

ˉ]dependsonasupplier’se?ciencyandisprivateinformationofthesupplier.costc∈[c

Followingthetraditionineconomicstheunitproductioncostisalsocalledthetypeofasupplier.Withinthepriorknowledgeofthebuyer,theproductioncostofeachsupplierfollowsanindependentandidenticalprobabilitydistributionF(c),withthedensityfunctionf(c).Theprobabilitydensityoftheminimumtypeamongthensuppliersisdenotedbyf(1)(c)=n(1?F(c))n?1f(c).WeassumethatF(c)/f(c)isanon-decreasingfunctionofc1.LetJ(c)=c+F(c)/f(c):J(c)iscalledthevirtualtypeofasupplier.Inadditionweassumethattherevenuerisbigenoughsothatr?J(ˉc)≥k.2

Generallyanauctionmechanism(B,κ,μ)hasthefollowingcomponents:asetofpossiblemessages(or“bids”)Biforeachbidderithatspeci?esthebiddingrule;awinnerdetermi-nationrule(or“allocationrule”)κ:B→PthatdeterminestheprobabilityPithatabidderiwillwinacontract,basedonthemessagesbsubmittedbyallbidders;acontractingruleμspeci?es,againasafunctionofallthemessagesb,thecontractμi(b)∈Tthatwillbeawardedtoeachbidderi[12].Anoptimalauctionmechanismisanauctionmechanismthatbringsthebestexpectedutilitytothebuyeramongallauctionmechanisms.Amechanismisindividuallyrational(IR)iftheexpectedutilityofaplayerinthismechanismisnon-negative.IRisanecessarypropertytoensurevoluntaryparticipation:onecannotforceaplayertoparticipateinthegameandacceptadealthatisworsethantheplayercouldgetoutside.Aswedonotassumeanyrestrictionsonthepossiblemessagesorthebiddingrules,thespaceofmechanismscouldbeenormouslylarge.OnespecialandsimpleclassofmechanismsareManyprobabilitydistributionssuchastheBetadistribution,whichhastheuniformdistributionasaspecialcase,satisfythiscondition.Pleasereferto[16]foranextensivediscussiononthosedistributions2Thisconditionensuresthatitispro?tableforthebuyertocontractwitheventheleaste?cienttypeofasupplier,asisshowninSection4and5.Withoutthisassumption,de?nec?suchatr?J(?c)=k.Thenthebuyerwillonlycontractwithasupplierwithc≤c?.Orequivalentlywecantreatc?astheupperboundcˉofasupplier’stype.1

5

calleddirectmechanisms.Inadirectmechanismeachbidderisaskedtodirectlyreporthertype,whichistheunitproductioncostinoursituation.Inotherwords,themessagespaceisthesameasthetypespaceinadirectrevelationmechanism.Adirectmechanism(L,M)consistsofapairoffunctions:L:[,ˉc]n→PandM:[ˉc]n→T,whereLi(c)istheprobabilitythatiwillwinacontractandMi(c)isthecontractawardedtoi[12],shouldibeoftypec.Amechanismisincentivecompatible(IC)ifitisthebeststrategyforabiddertotruthfullyrevealherprivateinformation:ICimpliesthattheexpectedutilityofasupplierismaximizedbytruthfulbidding,ortruthfulbiddingconstitutesaBayes-Nashequilibrium[11].InadirectICmechanism,eachbidderwillreporthertruetype.

Basedontherevelationprinciple,givenamechanismandanequilibriumforthatmechanism,thereexistsadirectmechanisminwhichitisanequilibriumforeachbiddertoreporthertypetruthfully,andtheoutcomeisthesameasinthegivenequilibriumoftheoriginalmechanism[12].TherevelationprincipleimpliesthattheoptimalmechanismamongdirectICmechanismsisalsooptimalamongallmechanisms.Despitethisfact,directICmechanismsarerarelyusedinpracticebecausetheyusuallyconsistofcomplexandun-intuitivewinnerdeterminationrulesandcontractingrules,sacri?cingtheadvantagesofasimplebiddingruleandbiddingstrategy.Buttheoutcomeofanoptimaldirectrevelationmechanismtellsthebestresultthatthebuyercanachieveinallpossiblemechanisms.

Inanauctionwithamenuofcontracts,thebuyerannouncesamenuofcontractsandeachsupplierbidsbyselectingonecontract.Thebuyerselectsthewinnerasthesupplierwhobidsthehighestrankedcontract,andthewinnerisawardedthatcontract3.

Inanauctionwithascoringrulethesuppliersaretheoneswhoproposecontracts,whichareevaluatedbythebuyerbasedonthescoringrule.Anauctionwithascoringrulecanbeaone-shotauction,inwhicheachsuppliersubmitsacontractonceinasealedbid,afterwhichthewinnerisselectedandthecontractisdecidedbasedonthebids;oritcanbeadynamicauction,inwhichsupplierscanupdatetheirbidsbasedonthecurrentbiddinginformation.AnEnglishauctionisonesuchdynamicauctionprotocolcommonlypracticed.WewillconsiderareverseEnglishauction,inwhichthesellers,seekingacontractwiththebuyer,startwithhigh“prices”anddecreasetheirbidssequentially.WepresentanoptimalauctionwithascoringruleinanEnglishauctionprotocol.Thesamescoringfunctioncanbeusedina?rst-scoreorsecond-scoresealed-bidauction,whichwillresultinthesameoptimaloutcomewithdi?erentbiddingstrategies.4InanEnglishauctionwithascoringrule,thebuyerannouncesascoringruleasafunctionofthenegotiableattributes,andthesuppliersbidbyeachsubmittingacontract.Theprovisionalwinneristhesupplierwhobidsthecontractwiththehighestscore,andthesupplieristentativelyawardedthecontractthatshe

Iftherearemorethanonesupplierwhobidthesamehighestrankedcontract,thetieisbrokenrandomlywithevenprobabilities.

4Thecounterpartsof?rst-priceandsecond-pricesealed-bidauctionsinamulti-attributeworldcanbecalled?rst-scoreandsecond-scoresealed-bidauctions.Inboththeseauctionsthebidderwiththehighestscoredbidwinstheauction.Inthe?rst-scoresealed-bidauctionthewinnerisawardedthecontractthatshebids.Inthesecond-scoresealed-bidauctionthewinnercanchooseanycontractthathasthesamescoreasthesecondhighestscoresubmittedbythebidders.3

6

bid5.Informedofthewinningcontractandscore,ineachroundtheothersupplierswhoarenotthewinnermayupdatetheirbidstooutbidthecurrentwinningcontractwithrespecttothescore6.Thesupplierswhocannotincreasetheirscoresquittheauctionandwillnotparticipateintherestofthebiddingprocess.Ifallsuppliers,excepttheprovisionalwinner,havequit,thentheauctionendsandtheprovisionalwinnerisawardedthewinningcontract.InSections4and5wepresentoptimalauctionmechanismsforaoptioncontractandawholesalepricecontractwithafranchisefee.We?rstderivetheoptimaldirectmechanismasabenchmarktoobtaintheoptimaloutcomethatthebuyercanachieveamongallauctionmechanisms(Section4.1and5.1).Thenweshowhowtheoptimaloutcomecanbeachievedwithanauctionwithamenuofcontracts(Section4.2and5.2)andanauctionwithascoringrule(Section4.3and5.3).

4Auctionsforanoptioncontract

Anoptioncontracthasthreeessentialnegotiableterms:theoptionquantityQO,theoptionpricewoandtheexercisepricewe.TheoptionquantityQOspeci?esthenumberofunitsofthecapacitythatthebuyerwantsthesuppliertopreparebeforetheseason,equivalentlythemaximumnumberofproductunitsthatthebuyercanorder.Foreachunitofcapacity(option),thebuyerpaysthesuppliertheoptionpricewo.Afterobservingthedemand,thebuyerplacesordersfortheproductduringtheseason.Foreachproductunitthatisordered,thebuyeradditionallypaystheexercisepricewe.RecallthatS(QO)isequaltotheexpectedsalesgivenacapacityofQO.

Givenanoptioncontract(wo,we,QO),theutilityofabuyerisequaltotheexpectedrevenue

b(w,w,Q)=(r?w)S(Q)?wQ,andtheutilityofasupplierisequalminusthefees:πOoeeoOOO

totheexpectedtotalpaymentfromthebuyerminusthecostonthecapacityandproduction,

s(c,w,w,Q)=(w?c)S(Q)?(k?w)Q.whichisrelatedtothesupplier’stypec:πOeeoOOOO

4.1Theoptimaldirectmechanism

Inanoptimaldirectmechanisminwhichthereisasinglewinner,themoste?cientsupplier,orthelowestc,mustbeawardedacontract.Otherwisethebuyercouldalwaysselectamoree?cientsupplierandbothcouldachievehigherpro?t.ThereforeanoptimaldirectmechanismisequivalenttodesigningacontractTO(c)=(wo(c),we(c),QO(c))foreachtypec.Atthebeginningoftheauctionthebuyerannouncesthecontractassociatedwitheachreportedtype,thenthesuppliersbidtheirtypes.Thesupplierwhobidsthelowesttypeisselectedasthewinnerandawardedthecontractcorrespondingtothereportedtype.Based

Againiftherearemorethanonesupplierwhobidthesamecontract,thetieisbrokenrandomlywithequalprobabilities.

6Toensuretheauctionterminatesin?nitetime,usuallyabidderisrequiredtoincreasethescoreofherbidbyanincrementnolessthanaspeci?edminimum.5

7

ontherevelationprinciple,wecanrestrictourmechanismstoICmechanisms,andstilldesignanoptimaldirectmechanism.

s(c??,c)betheutilityofasupplierwithtypecwhenshereportsthetypec??andthusLetπOs(c??,c)=[(w(c??)?c)S(Q(c??))+(w(c??)?choosesatypec??contractfromthebuyer.πOeoO????n?1ssk)QO(c)](1?F(c)).Letπ(c)=π(c,c),givenourmodeloftheprobabilitydistributionofsuppliers’types.Lemma4.1givestheconditionforamechanismbeingIC:

Lemma4.1Adirectmechanismisincentivecompatibleifandonlyif

(1)Theexpectedutilityofasuppliersatis?esthat

sπO(c)=u0+??ccˉS(QO(ρ))(1?F(ρ))n?1dρ(1)

whereu0isaconstant.

(2)QO(c)isanon-increasingfunctionofc.

Equation(1)impliesthatπs(ˉc)=u0,andπs(c??)≥πs(c)forc??≤c.Theconstantu0doesnotin?uencethechoiceofasupplier,wecanthushaveu0=0tomaximizethebuyer’sutility(ortominimizeasupplier’sutilitywiththesamecapacityinvestment)whilesatisfyingIR.??cˉˉ??csBasedonLemma4.1,theexpectedutilityofthewinningsupplierisπˉ=ccS(Q(ρ))(1?F(ρ))n?1dρf(1)(c)dc,whichcanbereformed,byinterchangingtheorderofintegration,as

πˉ=s??

ccˉS(QO(c))

??F(c)f(c)dc.f(c)(1)ˉThentheexpectedutilityofthebuyer,πˉb=cc[(r?c)S(Q(c))?kQ(c)]f(1)(c)dc?πˉs,isequal

to??cˉbπˉ=[(r?J(c))S(QO(c))?kQO(c)]f(1)(c)dc.c

Maximizingthebuyer’sexpectedutilityleadstoanoptimaldirectmechanism:

Proposition4.2Inanoptimaldirectmechanism,thenumberofoptionsintheoptioncon-tractis

ˉ?1(QO(c)=Gk),r?J(c)(2)

andtheoptionpricewo(c)andexercisepricewe(c)satisfy

??cˉ

Wo(c)+We(c)=cS(QO(ρ))(1?F(ρ))n?1dρ+cS(QO(c))+kQO(c),(1?F(c))(3)whereWo(c)=wo(c)QO(c)isthetotalpremiumfee,andWe(c)=we(c)S(QO(c))isthetotalexpectedexercisefee.

8

Wecannowcharacterizetheoptimaloutcomeofanoptioncontractauction:

1.Themoste?cientsupplieristhewinner,i.e.,theprobabilitythatthewinnerhasatypecisequaltof(1)(c)=n(1?F(c))n?1f(c).

2.Thecapacityinvestmentofthewinner,shouldshebeoftypec,isequaltoQO(c)=ˉ?1(k/(r?J(c))).G

3.Theexpectedutilityofthebuyerisequaltoπˉb=??cˉ

c[(r?J(c))S(QO(c))?kQO(c)]f(1)(c)dc.

??cˉ

c4.Theexpectedutilityofasupplierisequaltoπˉs(c)=S(QO(ρ))(1?F(ρ))n?1dρ.

Wecancomparethisoutcomewiththeoutcomeofanadvanced-purchasecontractauction.Anadvanced-purchasecontractspeci?esadeterministicnumberofproductunitsthatthebuyerordersfromthesupplier,alongwiththepaymentfromthebuyerfortheorder.Thusthistypeofcontracthasno?exibility.Suchacomparisonbetweenthebuyer’sexpectedutilitiesinbothcontractauctionsisprovidedinAppendix.Itshowsthatthebuyerachieveshigherexpectedutilitybyauctioninganoptioncontractascomparedtoanadvanced-purchasecontract.Anymechanismthatresultsinthesameoutcomeasdescribedaboveisanoptimalmechanism.Wenowusethisfacttoshowournexttwoauctionmechanismsareoptimal.

4.2Optimalauctionwithamenuofcontracts

Inanauctionwithamenuofcontracts,thedesignofthemenu,basedontheexpectationofthebiddingstrategiesofsuppliers,isthekeydecisionofthebuyer.Themenuofcontractscanberegardedascontractcustomizationfordi?erenttypesofsuppliers.Di?erenttypesofsupplierstradeo?thecapacityandpaymentdi?erently.Byo?eringdi?erentcombinationsofthenumberofoptionsandthepayment,thebuyerisabletocustomizethedesignofthecontractswithrespecttothesupplier’stype.Thisallowshertoextractmorepro?tfromthesystemwhenusingamoree?cientsupplier.Intheoptimaldirectmechanismwehavedesignedacontract(wo(c),we(c),QO(c))foreachtypecofasupplier.Givenamenuofthesecontracts,theauctionisoptimalifeachsupplierwillchoosethecontractdesignedforhertypebasedonthebiddingstrategytomaximizeherownexpectedutility.Proposition4.3establishesthatthecontractsintheoptimaldirectmechanismcomposeanoptimalmenuofcontracts.

Proposition4.3GivenamenuofcontractsTOwhereTO(c)=(wo(c),we(c),QO(c))satis-?esEquations(2)and(3),itisaBayes-NashequilibriumstrategyforasupplierctobidthecontractTO(c).TheauctionwiththemenuofcontractsTOresultsintheoptimaloutcome.

9

4.3Optimalauctionwithascoringrule

Inthisprotocolsuppliersbidcontracts,whichareevaluatedwithascoringrule.Letthescoreofacontractbid(wo,we,QO)bedenotedbysO(wo,we,QO).Areasonablescoringrulewillattachahigherscoretoacontractwithlowerpaymentorhighercapacity(optionquantity).Ifthevalueofthecapacitycanbemeasuredwithmonetaryvaluesindependentofthepayment,thenthescoringrulecanbeexpressedasaquasi-linearfunction:sO(wo,we,QO)=uO(QO)?(weS(QO)+woQO),whereuO(QO)isafunctionthatevaluatesthecapacityQOinmonetaryvalue,andweS(QO)+woQOistheexpectedpayment.Withsuchaquasi-linearscoringruletheoptionquantitythatasupplierwillbiddoesnotdependonthescore,butonlythescoringruleandthesupplier’stype[4].

Lemma4.4TheoptimalquantityQO(c)intheoptimalbidofasupplierwithtypecsatis?esdˉuO(QO)=cG(QO)+k.

OnemightthinkthatthebuyercouldsimplydesignthescoringruleaccordingtoherutilityfunctionandletuO(QO)=rS(QO).Thiswouldworkifthepro?tofatypeisindependentofthecapacitydecisionofothertypes,whichisthesituationwhenthebuyerhascompleteinformation.Butifthetypeisprivateinformationofasupplier,thecapacitydecisionofonetypealsoin?uencestheutilityofthetypesthataremoree?cient,andthusalsotheexpectedpro?tofthebuyerfromthosetypes.ThiscanbeseenfromEquation(1),whichsaysthattheexpectedutilityofasupplierisanincreasingfunctionofthelesse?cienttypes’quantities.Thereforeforthebuyerawardinganoptionquantitytoonetypecostssomepro?tfromthemoree?cienttypes.Basedonthisconsiderationthebuyerwillinduceadownwarddistortionofthecapacitydecisionfromthelevelthatwouldbeoptimalbasedonthebuyer’sutilityfunction.Thedownwardfactorinthescoringfunctioncanbedenotedby?(Q)>0,andthescoringruleiss(wo,we,Q)=(r?we)S(Q)?woQ??(Q).Considerthefollowingscoringrule:??QF(c(q))ˉG(q)dq(4)s(wo,we,Q)=(r?we)S(Q)?woQ?hf(c(q))

wherehisaconstant,andc(q)isthetypethatisawardedoptionquantityqintheoptimalˉ(q)=k/(r?J(c)).outcome:G

Proposition4.5WiththescoringruledescribedinEquation(4),theauctionachievesthesameoutcomeastheoptimalauctionmechanism.

ThestrategyofabidderinanEnglishauctionissimple.ThesupplierintypecwillbidtheoptionquantityfollowingLemma4.4,anddecreasewoand/orweeachtimeinthesmallestamounttooutbidthewinningcontract,untilthecontractbringszeropro?t.Thehighestscorethatasupplierccanreachisequaltou(Q)?(cS(Q)+kQ),withthetotalpaymentwoQ+weS(Q)equaltothetotalcostkQ+cS(Q).

10

5Auctionsforawholesaleprice-franchisefee(WF)contractWithanoptioncontractthebuyercanreservecertaincapacityatasuppliertoensuree?cientsupplywhenthecapacityisobservable.Butasupplier’spromiseonthecapacitycannotbeenforcedwhenthecapacityisunobservable.Thereforethecontractwithunobservablecapacityshouldnotinvolveanypromiseorcommitmentonthequantity,asthewholesaleprice,thepricethatthebuyerwillpaythesupplierforeachproductthatisprovided,istheonlycontracttermthatwillin?uencethesupplier’scapacitydecision.Ifthebuyerpromisesahigherwholesaleprice,thesupplierwillbuildmorecapacitybecauseofthehighermargin,butthemarginofthebuyerwillbelower.Thebuyer’sdesignofthewholesalepricehastotradeo?themarginofrevenueandthecapacityincentive.Inadditiontothewholesalepricethesupplycontractcanalsoincludeafranchisefeewhichisindependentoftheamountofsupply.Afranchisefeeallowsthebuyertoextractsome?xedamountofpro?tfromthesupplier.Thefranchisefeewillbehigherifthewholesalepriceislower.Supplierswithdi?erentproductioncostswilltradeo?thewholesalepriceandfranchisefeedi?erently.Combiningthesetwoattributesallowsthebuyertodi?erentiatethesuppliers’typesbyprovidingdi?erentpro?les.Wecallacontractinthisoriginalformawholesaleprice-franchisefee(WF)contract.

LetaWFcontractbedenotedby(w,t),wherewisthewholesalepricepaidbythebuyerandtisthefranchisefeepaidbythesupplier.GivenaWFcontract(w,t),asupplierchastodecidehercapacityQtooptimizeherexpectedutility(w?c)S(Q)?kQ?t,whichgivesˉ(QW(w,c))=k.TheexpectedutilityofthetheoptimalcapacityQW(w,c)satisfyingGssuppliercwiththecontractisπW(c)=(w(c)?c)S(QW(w,c))?kQW(w,c)?t,andthe

b=(r?w)S(Q(w,c)).expectedutilityofthebuyerisπWW

5.1Theoptimaldirectmechanism

InadirectmechanismthebuyerwillannounceaWFcontract(w(c),t(c))foreachtypeofsupplierc,andsuppliersbidbyreportingtheirtypes.Themoste?cientsupplierwillbeawardedthecontractcorrespondingtoherreportedtype.Asintheanalysisforoptioncontractauctions,wewill?rstderivetheconditionofanICmechanism,andthenreformtheexpectedutilityofthebuyerbasedontheICcondition,whichleadstotheoptimalICdirectmechanism.

s(ρ,γ)betheexpectedutilityofasupplierwiththetypeγbyreportingtypeρintheLetπWs(ρ,γ)=(w(ρ)?γ)S(Q(w(ρ),γ))?kQ(w(ρ),γ)?t.Letπs(ρ)=WFcontractauction,πWWWW??2?sssssssπW(ρ,ρ),πW,1(ρ,γ)=πW(ρ,γ),πW,2(ρ,γ)=πW(ρ,γ),andπW,12(ρ,γ)=πW(ρ,γ).Proposition5.1Anecessaryandsu?cientconditionofICisthat

s??(c)=?S(Q(c))(1?F(c))n?1,1.πW

s??2.πW,12(ρ,γ)≥0,whichisimpliedbyw(c)≤0.

11

Basedonthe?rstconditioninProposition5.1,theexpectedutilityofasuppliercinanoptimalincentivecompatiblemechanismis

sπW(c)=??ccˉS(QW(ρ))(1?F(ρ))n?1f(ρ)dρ(5)

whereQW(ρ)isthecapacitythatasupplierwithtypeρwillsetupgiventhecontractintheoptimalWFcontractauction.GivenEquation(5),theexpectedutilityofthebuyeris??ˉb=csπWc[(r?c)S(QW(c))?kQW(c)?π(c)]f(1)(c)dc,whichasbeforeisequalto

bπW=??ccˉ[(r?J(c))S(QW(c))?kQW(c)]f(1)(c)dc.(6)

TomaximizeherutilitythebuyershouldinducethecapacityinvestmentQW(c)bydesigningw(c)sothattheintegratedfunctioninEquation(6)ismaximized,iftheICconditioninProposition5.1canbesatis?ed.Maximizing(r?J(c))S(QW(c))?kQW(c)leadstotheˉ(QW(c))=k.Proposition5.2showsthatsuchcapacityinvestmentQW(c)thatsatis?esGcapacityinvestment,whichisthesameasintheoptimaloutcomewhencapacityisobservable,canactuallybeimplementedbyanoptimalWFcontractauctionwithunobservablecapacity.Proposition5.2AnoptimalWFcontractauctionwithunobservablecapacitiesimplementsanoptimaloptioncontractauctionwithobservablecapacities.InanoptimalWFcontractauction,thedesignofcontracts{(w(c),t(c))}satis?es

kF(c)w(c)=+c=r?f(c)G(Q(c))

??cˉ(7)

t(c)=ξ(Q(c))?cS(Q(ρ))(1?F(ρ))n?1dρ

(1?F(c))(8)

S(q)kˉ?1whereξ(q)=?q,andQW(c)=G()isthecapacitythatasupplierwillvoluntarily

choosestoset.

Onewouldexpectthatwhenasupplier’scapacityisunobservableandhencenotcontractable,theutilityofthebuyerwoulddecreasefromthesituationwithobservablecapacitysinceshehasonelesstermthatthecontractcanregulateupon.ButProposition5.2showsthatbycarefullydesigningthecontractformandtheauctionmechanism,thebuyerdoesnotloseutilitybecauseoflosingthiscontractableterm.Thebuyerinducesthesamecapacityinvestmentwiththewholesaleprice,andensuretheincentivecompatibilityofsuchcapacityinvestmentwiththefranchisefee.Ifthecontractonlyincludesthewholesaleprice,thecapacityinvestmentofasupplierwillbedi?erentbecausethenasuppliermaynotchoosethewholesalepricedesignedforhertype.

12

5.2Optimalauctionwithamenuofcontracts

TheWFcontractsdesignedforeachtypeofasupplierintheoptimaldirectmechanismcomposeanoptimalmenuofcontracts,andwiththismenuofcontracts,asupplierwithtypecwillselectthecontract(w(c),t(c)).

Proposition5.3GivenamenuofcontractsTWwhereTW(c)=(w(c),t(c))satis?esEqua-tion7and8,itisaBayes-NashequilibriumstrategyforasupplierctobidthecontractTW(c).TheauctionwiththemenuofcontractsTWresultsintheoptimaloutcome.

5.3Optimalauctionwithascoringrule

Letthescoringfunctionbede?nedasaquasi-linearfunction:sW(w,t)=?uW(w)+t.TheoptimalbidonthewholesalepricebyasupplierisgiveninLemma5.4,andisindependentofthescoreofthewholebid.

Lemma5.4Thewholesalepricewintheoptimalbidofasupplierwithtypecsatis?esdd[kQW(w,c)?(w?c)S(QW(w,c))]=uW(w)dwdw(9)

Toensurethewholesalepriceandhencethecapacityinvestmentarethesameasintheoptimaloutcome,thebuyerwoulddesignthefunctionuW(w)sothatEquation9issatis?ed

(c)atw=r?F

.Considerthefollowingscoringrule:

sW(w,t)=??w

α?S(QW(?,c(?)))d?+t(10)

whereαisaconstant,andc(w)isthetypecorrespondingtothewholesalepricewinthe

(c(w))optimalmechanism,i.e.,w=r?F

.

Proposition5.5WiththescoringruledescribedinEquation10,theauctionachievestheoptimaloutcome.

Asupplier’sbeststrategyissimple:Inthebeststrategyasuppliercwillalwaysbidthe(c)wholesalepricew(c)=r?F

followingEquation9.Asupplierwillsequentiallyincrease

thefranchisefeeuptothelevelthatbringszeropro?tinexpectationgiventhewholesaleprice.

13

6Electroniccontractingimplementation

Thissectionprovidesanoverviewofanimplementationofthemechanismsdiscussedinearliersections.We?rstpresenttheRETSINAarchitecture[18],amulti-agentplatformthatprovidesmuchoftheinfrastructureforautomatedcontracting.Wethenpresentthecontractnegotiationprocess,asitwouldtakeplacewithinRETSINAanddiscussthedesignofacontractingagent,responsibleforcoordinatingthenegotiationprocessandproducingthe?nal,executablecontract.

6.1TheRETSINAmulti-agentarchitecture

RETSINA(ReusableEnvironmentforTaskStructuredIntelligentNetworkedAgents)[18]providesanenvironmentforalooselycouplednetworkofsoftwareagentstointeracttosolveproblemsthatarebeyondtheindividualcapacitiesorknowledgeofeachproblemsolver.RETSINAenablesheterogeneousagentsthataredistributedacrossnetworkstocollaboratetoperformtasks.Itisthereforewell-suitedasaplatformtoimplementthecontractingmechanismsdiscussedinprevioussectionsofthepaper.

EachRETSINAagento?ersasetofservices,de?nedbytheagent’scapabilities.Inordertoaccomplishitstasks,eachagenthascommunicationandplanningmodules.Thecom-municationmodulesends,receivesandinterpretsmessagesandrequestsfromotheragents.Theplanningmoduletakesasetofgoals,suchassecuringacontract,andproducesaplanortaskstructuretosatis?estheagent’sgoals.RESTINAprovidesseveraldi?erentkindsofagentsthatinteracttocollectivelyaccomplishauser’sobjectives.WedescribetheRETSINAarchitecture,asusedforelectroniccontracting,below(Figure1).

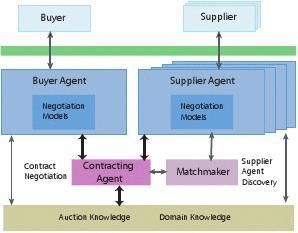
In:Interface

AgentsBuyer/Supplier

Out:

ContractsTaskAgents

MiddleAgents

Information

AgentsFigure1:ElectronicContractingusingtheRETSINAmulti-agentarchitecture

Ourscenarioassumesasinglebuyerandmultiplesuppliers.Throughinterfaceagents,thebuyerandthesupplierssubmittheirpreferencesforcontractstothebuyerandsupplier

14

agentsrespectively.ThebuyerandsupplieragentsareimplementedastaskagentswithinRETSINA.Taskagentshelpusersperformtasks,formulateproblem-solvingplansandcarryouttheseplansbycoordinatingandexchanginginformationwithotheragents.Thebuyerandsupplieragentshaveanadditionalmodule,whichencapsulatesthenegotiationdecisionmodelsdiscussedinthispaper.Thedecisionmodelsusethepreferencesofthebuyertogenerateacontractingmechanism,forexampleamenuofcontractsorascoringrulefortheevaluationofcontracts.Itisthenpassedontoacontractingagent,whichlocatessupplieragentsthroughaMatchmakerandcoordinatesthecontractnegotiationprocess.

TheMatchmakerisaRETSINAmiddleagent[19],helpingmatchagentsthatrequestser-viceswithagentsthatprovideservicesinthesystem.Forexample,thecontractingagentcanquerytheMatchmakerforsupplieragentsthathaveregisteredwiththeMatchmakerpreviously.Thecontractingagentisitselfamiddleagent,inthatitcoordinatestheactualcontractnegotiation,matchingabuyeragentwiththebestsupplieragentanddrawingupanexecutablecontract.

Allagentsinvolvedinthecontractnegotiationprocessmaymakeuseofinformationagents,whichprovideaccesstoinformationfromheterogeneousinformationsources,suchasdatabasesandknowledgebases.Forelectroniccontracting,informationagentsprovidetheagentsin-volvedinthecontractnegotiationwithdomainknowledge,suchasthedemandforecastin-formation,capacitycostandthegeneralproductione?ciencyofsuppliers.Furthermore,theinformationagentsprovidegeneralknowledgeaboutdi?erentkindsofauctionmechanisms,suchasauctionswithamenuofcontracts,withscoringrules,?rstpriceandsecond-pricesealedbidauctions,etc.

Thus,severaldi?erentkindsofagentsparticipateinthecontractnegotiationprocess.Inthenextsection,wedescribethecontractnegotiationprocessindetail.

6.2TheContractNegotiationProcess

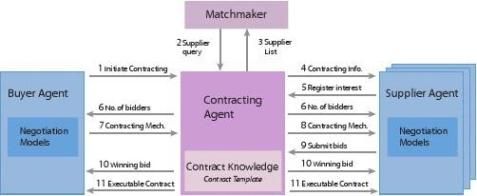
Figure2:TheContractNegotiationProcess

15

Thecontractnegotiationisamulti-agenttransaction,involvingabuyeragent,severalsupplieragents,acontractingagentandamatchmaker.Inordertoinitiateacontractnegotiationusingaparticularauctionprotocol,thebuyeragent?rstneedstolocateacontractingagentthatsupportsthedesiredauctionprotocol.ThenegotiationprocessthatfollowsisdisplayedinFigure2andissummarizedinthefollowingsteps:

1.Thebuyeragentcontactsthecontractingagenttoinitiateacontractnegotiation.Itsrequestincludesinformationaboutthesupplyorservicetocontracton,e.g.theproductsupplyforthenextdemandseason,thecontractform(e.g.anoptioncontractorwholesaleprice-franchisefee(WF)contract)andtheauctionprotocol.

2.ThecontractingagentsendsaqueryrequesttotheMatchmakeraboutsupplieragents.

3.TheMatchmakerreturnsalistofsupplieragentstothecontractingagent.

4.Thecontractingagentcontacts(asubsetof)thesupplieragentswithcontractinginformation,suchasthecontractingrequirementanddemand,thecontractformandtheauctionprotocol.

5.Thesupplieragentsinformthecontractingagentoftheirinterestinparticipatinginthecontractnegotiation.

6.Thecontractingagentsendsnegotiationinformationtoallbuyerandsupplieragents.Thenegotiationinformationconsistsofthenumberofbiddersparticipatinginthenegotiationandacontracttemplate,whichdescribesthecontractparameters,suchaspriceofgoods,andwhethertheyareundernegotiation.

7.Thebuyeragentsendsthecontractingagentthemechanism,forexamplethemenuofcontractsorascoringrule,thatwillbeusedforthecontractnegotiation.

8.Thecontractingagentsendsthecontractingmechanisminformationtothesupplieragents.

9.Thesupplieragentsrespondbysubmittingcontractbidstothecontractingagent.

10.Thecontractingagentselectsthewinningbidandinformsallpartiesofthewinningbid.

11.Inthecaseofadynamicauctionwithmultiplerounds,steps9and10(thesupplieragents

submitcontractbidsandthecontractingagentselectsthewinningbid)arerepeated.Afterthelastroundofthecontractingprocess,thecontractingagentconstructsanexecutablecontractfromthecontracttemplateandtheresultsofthecontractnegotiation.Thisexecutablecontractissenttoboththebuyeragentandthewinningsupplieragent.

Thecontractingagentgeneratesacontracttemplatefromthebuyeragent’sinformationinstep1andtheexecutablecontractinstep11,usingitsknowledgeaboutcontractsandtheexecutionenvironmentofthecontract.Aninterestingapproachtotherepresentationofcontractknowledge,contractsandcontracttemplatesisprovidedbytheContractBot[15]framework,whichusesdeclarativerepresentationsofacontracttemplatetonegotiateafullexecutablecontract.ContractBotusesCourteousLogicPrograms(CLP)[14]torepresentcontractsandcontracttemplates.Courteouslogicprogramsenablethespeci?cationofthescopeofpotentialcon?ictwithincontracts,suchasmutuallyexclusivecontractcon?gura-tions,andspeci?cationofpartially-orderedprioritiesbetweenrules,whichisusedtoresolveinconsistenciesbetweentherules.

16

Acknowledgement

ThisworkwassupportedinpartbyAFOSRgrantF49620-01-1-0542andAFRL/MNKgrantF08630-03-1-0005.

References

[1].

[2]S.AngelovandP.Grefen.B2Becontracthandling-asurveyofprojects,papersandstandards.Technicalreport,UniversityofTwente,TheNeterlands.

[3]G.CachonandF.Zhang.Fastdeliverythroughcompetingsuppliers.MSOM2003.

[4]Y.-K.Che.Designcompetitionthroughmultidimensionalauctions.RANDJournalofEconomics,24(4):668–680,1993.

[5]F.Chen.Auctioningsupplycontracts.Technicalreport,GraduateSchoolofBusiness,ColumbiaUniversity,2001.

[6]S.DasguptaandD.F.Spulber.Managingprocurementauctions.InformationEconomicsandPolicy,4:5–29,1989/90.

[7]Y.B.DawnBarnes-SchusterandR.Anupindi.Optimizingdeliveryleadtime/inventoryplacementinatwo-stageproduction/distributionsystem.Technicalreport,UniversityofChicago,2000.

[8]R.A.-S.EstherDavidandS.Kraus.AnEnglishAuctionProtocolforMulti-AttributeItems,volume2531ofAgentMediatedElectronicCommerceIV:DesigningMechanismsandSystems,LNAI,pages52–68.2002.

[9]R.A.-S.EstherDavidandS.Kraus.Protocolsandstrategiesforautomatedmulti-attributeauction.InProceedingsofthe3rdInternationalConferenceonAutonomousAgentsandMulti-AgentSystems(AAMAS2002),July2002.

[10]R.A.-S.EstherDavidandS.Kraus.Bidders’strategyformulti-attributesequential

englishauctionwithadeadline.InProceedingsofthe3rdInternationalConferenceonAutonomousAgentsandMulti-AgentSystems(AAMAS2003),July2003.

[11]D.FudenbergandJ.Tirole.GameTheory.MITPress,1991.

[12]V.Krishna.AuctionTheory.AcademicPress,2002.

[13]D.Lucking-ReileyandD.F.Spulber.Business-to-businesselectroniccommerce.Journal

ofEconomicPerspectives,15(1):55–68,Winter2001.

17

[14]D.M.Reeves,B.N.Grosof,M.P.Wellman,,andH.Y.Chan.Towardsadeclarative

languagefornegotiatingexecutablecontracts.InProceedingsoftheAAAI-99WorkshoponArti?cialIntelligenceinElectronicCommerce(AIEC-99),July1999.

[15]D.M.Reeves,M.P.Wellman,andB.N.Grosof.AutomatedNegotiationfromDeclarative

ContractDescriptions.November2002.

[16]K.Rosling.Inventorycostratefunctionswithnonlinearshortagecosts.Operations

Research,50(6):1007–1017,2002.

[17]J.SunandN.Sadeh.Coordinatingmulti-attributereverseauctionssubjecttotemporal

andcapacityconstraints.InProceedingsof2004HawaiiInternationalConferenceonSystemSciences(HICSS-37),January2004.

[18]K.Sycara,K.Decker,A.Pannu,M.Williamson,andD.Zeng.Distributedintelligent

agents.IEEEExpert,December1996.

[19]K.Sycara,K.Decker,andM.Williamson.Middle-agentsfortheinternet.InProceedings

ofIJCAI-97,January1997.

[20]W.E.WalshandM.P.Wellman.Decentralizedsupplychainformation:Amarket

protocolandcompetitiveequilibriumanalysis.JournalofArti?cialIntelligenceResearch,19:513–567,2003.

Appendix

ProofofLemma4.1:

ssNecessary:Ifthecontractisincentivecompatible,πO(c)=maxc??πO(c??,c).Withoutlossofgenerality

ssssssletc??>c.ICimpliesthatπO(c??,c)?πO(c??,c??)≤πO(c,c)?πO(c??,c??)≤πO(c,c)?πO(c,c??),whichis

ss(c??,c??)≤(c???c)S(QO(c))(1?F(c))n?1,equivalentto(c???c)S(QO(c??))(1?F(c??))n?1≤πO(c,c)?πOsπs(c,c)?π(c??,c??)S(QO(c??))(1?F(c??))n?1≤≤S(QO(c))(1?F(c))n?1.ThereforeS(QO(c))(1?

s??F(c))n?1isadecreasingfunctionofc.Whenc??→??c,theinequalityimpliesthatπO(c)=?S(QO(c))(1?cn?1sssn?1F(c)).LetπO(ˉc)=u0,thenπ(c)=π(ˉc)+c?S(Q(ρ))(1?F(ρ))dρ.ˉ??cssSu?cient:Assumetwotypesc??>c.GivenEquation1,πO(c??)?πO(c)=c??S(QO(ρ))(1?F(ρ))n?1dρ.??c??Buttherighthandsideisnogreaterthan≤c?S(QO(c??))(1?F(c??))n?1dρ=S(QO(c??))(1?

ssF(c??))n?1(c???c),sinceQO(c)≥QO(c??).ThereforeπO(c)≥πO(c??)?S(QO(c??))(1?F(c??))n?1(c?c??)=

s[We(c??)+Wo(c??)?kQO(c??)?cS(QO(c??))](1?F(c??))n?1=πO(c??,c).Hencethecontractisincentive

compatible.

ProofofProposition4.1:Weonlyneedtoprovethatthemechanismisincentivecompatible,sinceQO(c)inEquation2maximizesthebuyer’sexpectedutilitybasedontheassumptionthatthemech-

sssanismisincentivecompatible.WewillproveICbyshowingthatπO(c??,c)≤πO(c).πO(c??,c)=??cˉ

[(we(c)?c)S(Q(c))+(wo(c)?k)QO(c)](1?F(c))??????????n?1=[c??S(QO(ρ))(1?F(ρ))n?1dρ

+(c???c)S(QO(c??))](1?

18

F(c??))n?1=??cˉn?1??????n?1sS(Q(ρ))(1?F(ρ))dρ+(c?c)S(Q(c))(1?F(c)).π(c)=S(Q(ρ))(1?O??cc????cF(ρ))n?1dρ.Thenπs(c)?πs(c??,c)=cS(Q(ρ))(1?F(ρ))n?1dρ?(c???c)S(Q(c??))(1?F(c??))n?1≥??c??S(Q(c??))(1?F(c??))n?1dρ?(c???c)S(Q(c??))(1?F(c??))n?1=0.Thereforeasupplierwillbidctruthfully.??cˉ

Comparinganoptimaloptioncontractauctionandadvanced-purchasecontractauction:

Basedon[5],inanoptimaladvanced-purchasecontractmechanism,thequantityQA(c)thatthe

ˉ(QA(c))=k+J(c),theexpectedutilityofbuyerwillbuyfromawinnerwithtypecsatis?esthatG??cˉsn?1basuppliercisπA(c)=cQA(ρ))(1?F(ρ))dρ,andtheexpectedutilityofthebuyerisπA=??cˉ[rS(QA(c))?(k+J(c))QA(c)]f(1)(c)dc.c

LetIA(QA,c)=rS(QA(c))?QA(c)(J(c)+k)andIO(QO,c)=S(QO(c))(r?J(c))?kQO(c).Then??c??cˉˉbbπO=cIO(QO,c)f(c)dc,πA=cIA(QA,c)f(c)dc.QO(c)≥QA(c)becauseG(QA(c))?G(QO(c))=

bb+J(c)?r)≤0.ThenπO≥πA.ThisisbecauseIO(QO,c)≥IO(QA,c).ButIO(QA,c)?

IA(QA,c)=(QA(c)?S(QA(c)))J(c)≥0.J(c)(k

ProofofProposition4.3:Itsu?cestoprovetheincentivecompatibilityandfollowstheproofofProposition4.2.

ProofofLemma4.4:Foragivenscores,asupplierwillchooseqtomaximize(we?c)S(q)+(wo?k)q

?subjectto(r?we)S(q)?woq??(q)=s.LetW=weS(q)+woq.If((r?c)S(q)?kq??(q))=0,

forexample,rS??(q)????(q)>cS??(q)+k,thenwecanhaveq??=q+??for??>0verysmall,andW??=W+(rS(q??)+?(q??))?(rS(q)+?(q)).WithW??andq??,thescoreisthesame,butthesupplierhashigherutilitybecauseW???W?[(cS(q??)?kq??)?(cS(q)?kq)]=(rS(q??)+?(q??))?(rS(q)+?(q))?[(cS(q??)?kq??)?(cS(q)?kq)]=(rS??(q)????(q))???(cS??(q)+k)??>0.

ProofofProposition4.5:FollowingLemma4.4,asupplierwithtypecwillchoosetheoptionquantity

?QO(c)tomaximize(r?c)S(q)?kq??(q).Thisisbecause((r?c)S(q)?kq??(q))=(r?c?

independentofthescore.

Letsˉ(c)=(r?c)S(QO(c))?kQO(c)??(QO(c))bethemaximumscorethatcanbereachedbyasupplierwithtypec.Atthecontractwiththemaximumscoretheutilityofasupplieriszero.InanEnglishauction,themoste?cientsupplierwillbethewinnerbecausethemaximumscoreofamoree?cientsupplierishigher.Thereforetheprobabilityofbeingthewinner,andthecapacityinvestmentofthewinner,inanEnglishauctionarethesameasintheoptimalmechanism.FollowingtheproofofProposition4in[4],theEnglishauctionwiththescoringruleEquation4implementstheoptimalmechanism.

ProofofProposition5.1:ThecapacitydecisionofasupplierwithtypecisQW(c??,c)ifshereports

stypec??andisselectedasthewinner.πW(c??,c)=[(w(c??)?c)S(Q(c??,c))?kQW(c??,c)?t(c??)][1?

k?s???????????ˉ(QW(c??,c))=ˉF(c??)]n?1,G,πW(c,c)=[(w(c)?c)G(QW(c,c))QW(c,c)?S(QW(c,c))?

?kQW(c??,c)][1?F(c??)]n?1=?S(QW(c??,c))[1?F(c??)]n?1.

Necessary:

?sss??ICimpliesthatc=argmaxc??πW(c??,c).Bytheenveloptheorem,itfollowsthatπW(c)=πW(c??,c)|c??=c.

s??ˉ(QW(c))?QW(c??,c)|c??=c?S(Q(c))?k?QW(c??,c)|c??=c][1?F(c)]n?1=HenceπW(c)=[(w(c)?c)G?S(QW(c))[1?F(c)]n?1andthe?rstconditionshouldbesatis?edinanICmechanism.Actually1F(Q?(QO(c)))ˉO)G(q)?kf(QO(QO(c)))whichiszeroifq=QO(c).ThereforeasupplierwithtypecwillchooseQO(c)

19

ss??ssthe?rstconditionisequivalenttoπW,1(c,c)=0.ItisbecauseπW(c)=πW,1(c,c)+πW,2(c,c),and

s??sn?1sπW(c)=πW,ifπW,2(c,c)=?S(QW(c))[1?F(c)]1(c,c)=0,whichisimpliedbyIC.

ssssIfthemechanismisincentivecompatible,πW(c??,c)≤πW(c,c)andπW(c,c??)≤πW(c??,c??).Adding

ssssupthesetwoinequalitiesgivesπW(c??,c)?πW(c??,c??)≤πW(c,c)?πW(c,c??).Itisequivalentto??c????cssπ(ρ,γ)≤0,andimpliesthesecondconditionπW,12(ρ,γ)≥0.cc??W,12

Su?cient:

ssNowsupposeπW,12(ρ,γ)≥0andπW,1(c,c)=0.IfamechanismisnotIC,

ssπW(c??,c)>πW(c,c)???c??

?

?

?πs(ρ,c)dρ>0c??W,1??css[π(ρ,c)?πW,1(ρ,ρ)]dρc??W,1??c??csπ(ρ,γ)dγdρ>0ρW,12csπW,12(ρ,γ)<0.>0

sItcontradictstheconditionπW,12(ρ,γ)≥0.Thereforethe?rstandsecondconditionsaresu?cient

foranICmechanism.

?sn?1ˉ(QW(ρ,γ))?QW(ρ,γ)(1?F(ρ))n?1+(n?ButπW,]=?G12(ρ,γ)=?[S(QW(ρ,γ))(1?F(ρ))?1n?2??ˉ(QW(ρ,γ))=1)S(QW(ρ,γ))(1?F(ρ))f(ρ).Ifw(c)≤0,thenQW(ρ,γ)≤0becauseG.

Thereforew(c)≤0implies??sπW,12(ρ,γ)≥0.

ProofofProposition5.2:Itsu?cestoprovethatthismechanismisincentivecompatible.Basedon

(n?1)f(c)t??(c)dF(c)??ˉEquation8,?[t(c)?kξ(QW(c))]W=?=w(c).BecauseG(QW(c))=WF(c))(q)g(q)]=?S(QW(c))(1?F(c)),givenξ(q)=S

Therefore(t?kξ(QW(c)))(1?.??cˉsF(c))n?1=cS(Q(ρ))(1?F(ρ))n?1dρ.Thentheexpectedutilityofasuppliercis:πW(c)=[(w(c)?

kn?1c)S(QW(c))?t(c)?kQW(c)](1?F(c))n?1=[=WS(QW(c))?t(c)?kQW(c)](1?F(c))??cˉ[kξ(QW(c))?t(c)](1?F(c))n?1=cS(Q(ρ))(1?F(ρ))n?1.The?rstconditioninProposition5.1

issatis?ed.BasedontheassumptionthatF(c)/f(c)isanincreasingfunctionofc,w??(c)<0,andsothesecondconditionisalsosatis?ed.k??,w(c)n?1=dk+c)(=1+kg(QW(c))Q??W(c).Wn?1??Thesetwoequalitiessuggestd[(t?kξ(QW(c)))(1?

ProofofProposition5.3:Itsu?cestoprovetheincentivecompatibilityandfollowstheproofofProposition5.2.

ProofofLemma5.4:ItissimilartotheproofofseparabilityinLemma4.4.IfEquation9doesnothold,thesuppliercanalwaysincreasewanddecreasetiftherighthandsideisbigger,ordecreasewandincreasetifthelefthandsideisbigger,sothatthescoredoesnotchangebuttheutilitybasedonthecontractisincreased.

ProofofProposition5.5:FollowingLemma5.4,asupplierwithtypecwillchoosethewholesaleprice

(c)d??w(c)=r?F

becauseu(w)=S(QW(w,c(w)))isequalto[(w?c)S(QW(w,c))?kQW(w,c)]=

S(QW(w,c))whenw=w(c).HenceasupplierwithtypecwillbuildcapacityQW(c)thatisequaltotheoutcomeinanoptimalmechanism.Sincethemoste?cientsupplierwillbethewinnerinanEnglishauction,theEnglishauctionwiththescoringruleEquation10implementstheoptimalmechanism.

20