昆明理工大学
《 计 算 机 仿 真》
上 机 实 验 报 告
实验一 常微分方程的求解及系统数学模型的转换
一．实验目的
通过实验熟悉计算机仿真中常用到的Matlab指令的使用方法，掌握常微分方程求解指令和模型表示及转换指令，为进一步从事有关仿真设计和研究工作打下基础。
二. 实验设备
个人计算机，Matlab软件。
三. 实验准备
预习本实验有关内容（如教材第2、3、5章中的相应指令说明和例题），编写本次仿真练习题的相应程序。
四. 实验内容
1. Matlab中常微分方程求解指令的使用
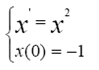题目一：请用MATLAB的ODE45算法分别求解下列二个方程。要求:1.编写出Matlab仿真程序；2.画出方程解的图形并对图形进行简要分析；3.分析下列二个方程的关系。
1． 2．
1.仿真程序
方程一:
M文件;
function f1=f1(t,x)
f1=-x^2
[t,x]=ode45(‘f1’,[0,40],[1]);
plot(t,x);
grid
方程二：
function f1=f1(t,x)
f1=x^2
[t,x]=ode45(f2,[0,40],[-1]);
plot(t,x);
grid
2.方程解的图形并对图形进行简要分析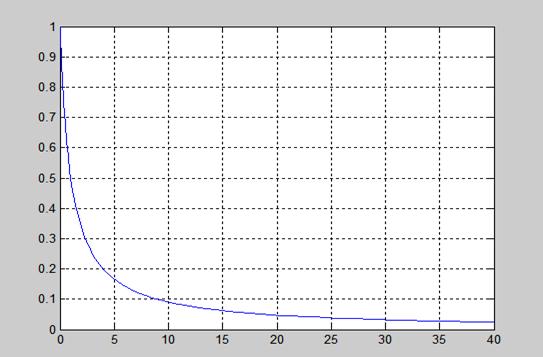
3.
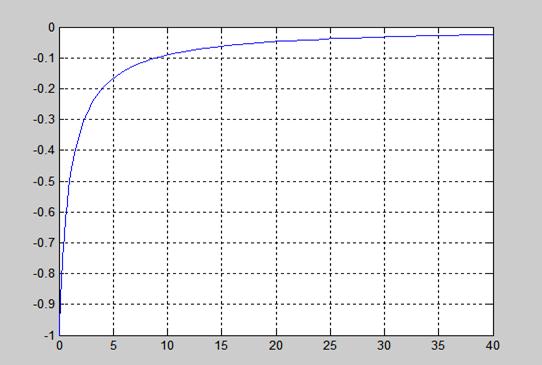
3.二个方程的关系
题目二：下面方程组用在人口动力学中，可以表达为单一化的捕食者-被捕食者模式（例如，狐狸和兔子）。其中
表示被捕食者， 
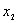表示捕食者。如果被捕食者有无限的食物，并且不会出现捕食者。于是有
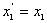，则这个式子是以指数形式增长的。大量的被捕食者将会使捕食者的数量增长；同样，越来越少的捕食者会使被捕食者的数量增长。而且，人口数量也会增长。请分别调用ODE45、ODE23算法求解下面方程组。要求编写出Matlab仿真程序、画出方程组解的图形并对图形进行分析和比较。
fun3 m文件：
function fun3=fun3(t,x)
fun3=[x(1)-0.1*x(1)*x(2)+0.01*t;-x(2)+0.02*x(1)*x(2)+0.04*t]
Ode45解函数程序：
[t,x]=ode45('fun3',[0,20],[30,20]);
plot(t,x);title('ode45作图');
xlabel('蓝线为捕食者，绿线为被捕食者');
grid
Ode45解函数图像：
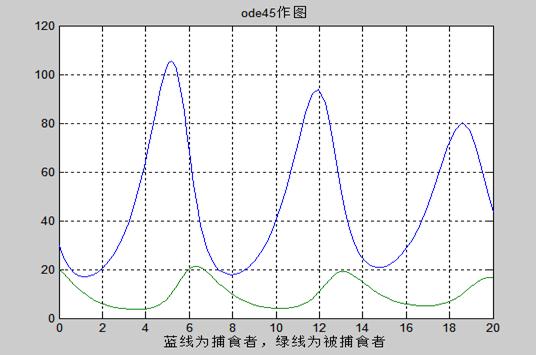
Ode23解函数程序：
[t,x]=ode23('fun3',[0,20],[30,20]);
plot(t,x);title('ode23作图');
xlabel('蓝线为捕食者，绿线为被捕食者');
grid
Ode23解函数图像：
2. Matlab中模型表示及模型转换指令的使用
题目三：若给定系统的的传递函数为
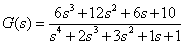
请用MATLAB编程求解其系统的极零点模型。
fz=[6 12 6 10];fm=[1 2 3 1 1];
[z,p,k]=tf2zp(fz,fm);
Gzpk=zpk(z,p,k)
[zero poles k]=zpkdata(Gzpk,'v')
结果：
Gzpk =
6 (s+1.929) (s^2 + 0.07058s + 0.8638)
-----------------------------------------------
(s^2 + 0.08663s + 0.413) (s^2 + 1.913s + 2.421)
Continuous-time zero/pole/gain model.
zero =
-1.9294 + 0.0000i
-0.0353 + 0.9287i
-0.0353 - 0.9287i
poles =
-0.9567 + 1.2272i
-0.9567 - 1.2272i
-0.0433 + 0.6412i
-0.0433 - 0.6412i
k =
6
题目四：习题2.4
的对角标准型
fz=[1 4 5] ;
fm=conv([1 1],[1 5 6]);
Gtf=tf(fz,fm);
diag=canon(Gtf,'modal')
结果：
diag =
a =
x1 x2 x3
x1 -3 0 0
x2 0 -2 0
x3 0 0 -1
b =
u1
x1 -15.52
x2 -19.6
x3 5.745
c =
x1 x2 x3
y1 -0.06442 0.05103 0.1741
d =
u1
y1 0
题目五：习题5.8
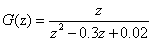采样周期 Ts=0.02s 先在t=0.1s仿真
fz=[1,0 ];
fm=[1 -0.3 0.02];T1=0.1;T2=0.02;
firstsys=tf(fz,fm,T1)
secondsys=d2d(firstsys,T2)
结果：
firstsys =
z
------------------
z^2 - 0.3 z + 0.02
Sample time: 0.1 seconds
Discrete-time transfer function.
secondsys =
0.278 z - 0.1369
----------------------
z^2 - 1.356 z + 0.4573
Sample time: 0.02 seconds
Discrete-time transfer function.
五．总结与体会
做完本次试验，学会了简单的matlab的编程，并学会了ode解函数的调用，以及状态空间表达式，传递函数，零极点传递函数模型建立与相互转换。
实验二 Matlab优化工具箱的使用
一．实验目的
通过上机操作熟悉Matlab优化工具箱的主要功能及其使用方法，掌握优化工具箱中常用函数的功能和语法，并利用其进行极值运算、求解线性和非线性问题等，为进一步的仿真设计和研究打下基础。
二. 实验设备
个人计算机，Matlab软件。
三. 实验准备
预习本实验有关内容（如教材第6章中的相应指令说明和例题），编写本次仿真练习题的相应程序。
四. 实验内容
1. 应用Matlab优化工具箱求解优化问题
例题6.6~6.10，选做2题，要求自行修改方程系数，并比较运行结果。
例6.6 求解非线性方程：
初始值为x0 = [-2 ,-2]
function F=f_fun(x);
F=[4*x(1)-2*x(2)-exp(-x(1));-2*x(1)+4*x(2)-exp(-x(2))]
x0 = [-2; -2];
options=optimset('Display','iter');
[x,fval] = fsolve('f_fun',x0,options)
结果：
x =
0.3517
0.3517
fval =
1.0e-10 *
-0.1949
-0.1949
6.8：利用Matlab命令求解下面的无约束非线性规划问题。
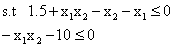
function f=f_fun1(x)
f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+2)
function [c1,c2]=f_fun2(x)
c1=1.5+x(1)*x(2)-x(1)-x(2);
c2=-x(1)*x(2)-10;
程序：
x0=[-1 1];
[x,f,exitflag,output]=fmincon(@f_fun1,x0,[],[],[],[],[],[],@f_fun2)
结果：
x =
-9.5474 1.0474
f =
0.0242
2. 应用Matlab优化工具箱求解极值问题
已知函数f(x)=10*exp(-x)*cos(x) ，求函数的极值。
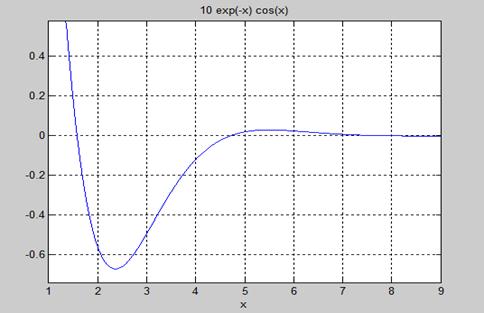
（1）x∈[2，5]时，求函数的最小值，并画出函数的曲线。
f=inline('10*exp(-x)*cos(x)');
ezplot('10*exp(-x)*cos(x)',[1,9]);
[x min]=fminbnd(f,2,5)
x =
2.3562
min =
-0.6702
（2）x∈[3，9]时，求函数的最大值，并画出函数的曲线。
分析：欲求原函数的最大值及为反函数的负的最小值。
f=inline('-10*exp(-x)*cos(x)');
ezplot('10*exp(-x)*cos(x)',[1,9]);
[x min]=fminbnd(f,3,9)
max=-min
x =
5.4978
min =
-0.0290
max =
0.0290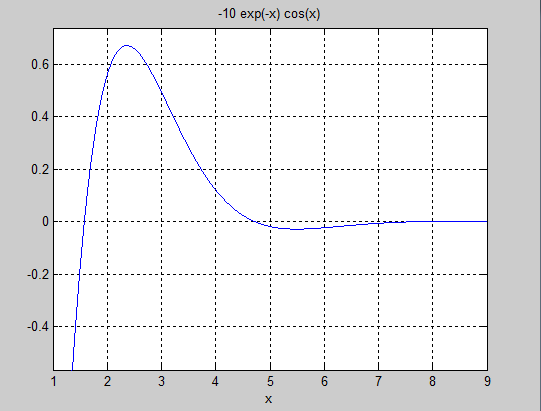
五．总结与体会
通过本次实验，熟悉了Matlab优化工具箱的主要功能及其使用方法，掌握了优化工具箱中常用函数的功能和语法，并学会利用其进行极值运算、求解线性和非线性问题。
验三利用Matlab和Simulink进行系统仿真设计
一．实验目的
通过实验对一个汽车运动控制系统进行实际设计与仿真，掌握控制系统性能的分析和仿真处理过程，熟悉用Matlab和Simulink进行系统仿真的基本方法。
二. 实验设备
个人计算机，Matlab软件。
三. 实验准备
预习本实验相关说明，复习PID控制器的原理和作用，明确汽车运动控制系统问题的描述及其模型表示，编写本次仿真练习的相应程序。
四. 实验说明
本实验是对一个汽车运动控制系统进行实际设计与仿真，其方法是先对汽车运动控制系统进行建摸，然后对其进行PID控制器的设计，建立了汽车运动控制系统的模型后，可采用Matlab和Simulink对控制系统进行仿真设计。
注意：设计系统的控制器之前要观察该系统的开环阶跃响应，采用阶跃响应函数step( )来实现，如果系统不能满足所要求达到的设计性能指标，需要加上合适的控制器。然后再按照仿真结果进行PID控制器参数的调整，使控制器能够满足系统设计所要求达到的性能指标。
五. 实验内容
1. 问题的描述
如下图所示的汽车运动控制系统，设该系统中汽车车轮的转动惯量可以忽略不计，并且假定汽车受到的摩擦阻力大小与汽车的运动速度成正比，摩擦阻力的方向与汽车运动的方向相反，这样，该汽车运动控制系统可简化为一个简单的质量阻尼系统。
根据牛顿运动定律，质量阻尼系统的动态数学模型可表示为：
系统的参数设定为：汽车质量m=1000kg，
比例系数b=50 N·s/m，
汽车的驱动力u=500 N。
根据控制系统的设计要求，当汽车的驱动力为500N时，汽车将在5秒内达到10m/s的最大速度。由于该系统为简单的运动控制系统，因此将系统设计成10％的最大超调量和2％的稳态误差。这样，该汽车运动控制系统的性能指标可以设定为：
上升时间：tr<5s；
最大超调量：σ％<10％；
稳态误差：essp<2％。
2.系统的模型表示
假定系统的初始条件为零，则该系统的Laplace变换式为：
即
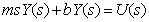
则该系统的传递函数为：
如果用Matlab语言表示该系统的传递函数模型，相应的程序代码如下：
sys=tf(1,[1000 50])
同时，系统的数学模型也可写成如下的状态方程形式：
如果用Matlab语言表示该系统状态空间模型，相应的程序代码如下：
Sys=ss([-0.5],[0.001],[1])
sys=ss(-0.05,0.001,1,0)
3. 系统的仿真设计
● 利用Matlab进行仿真设计
I．求系统的开环阶跃响应
在Matlab命令窗口输入相应的程序代码，得出该系统的模型后，接着输入下面的指令：
step(u*sys)
可得到该系统的开环阶跃响应曲线，如下图所示：
step(500*sys)
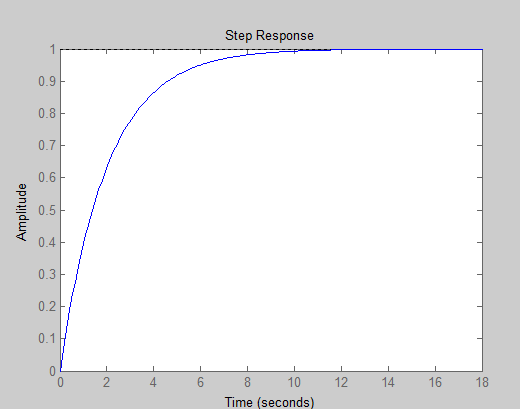
从图上可看出该系统不能满足系统设计所要求达到的性能指标，需要加上合适的控制器。
II．PID控制器的设计
PID控制器的传递函数为：
在PID控制中，比例（P）、积分（I）、微分（D）这三种控制所起的作用是不同的（请注意在实验总结中进行归纳）。下面分别讨论其设计过程。
（1）比例（P）控制器的设计
增加比例控制器之后闭环系统的传递函数为：
由于比例控制器可以改变系统的上升时间，现在假定Kp＝100，观察一下系统的阶跃响应。在MATLAB命令窗口输入指令：
Gs=tf(100,[1000 150]);
Step(500*Gs)
可得系统阶跃响应如下：
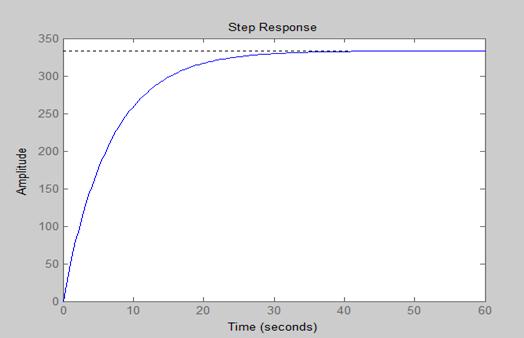
由此仿真结果，分析系统的稳态值是否满足设计要求，系统的稳态误差和上升时间能不能满足设计要求？
稳态误差：ess=
=66.7％。
上升时间：Tr=40s.
因而稳态误差和上升时间都不能满足要求。
若减小汽车的驱动力为10N，重新进行仿真，仿真结果为：
Gs=tf(100,[1000 150]);
Step(10*Gs)
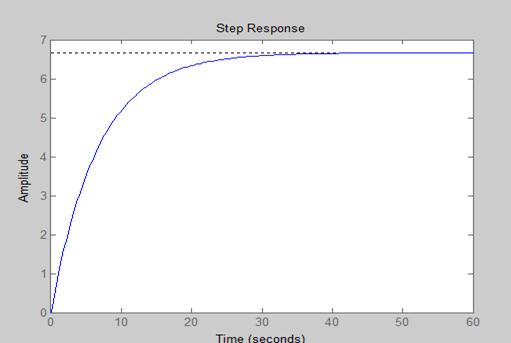
如果所设计的比例控制器仍不能满足系统的稳态误差和上升时间的设计要求，则可以通过提高控制器的比例增益系数来改善系统的输出。例如把比例增益系数Kp从100提高到10000重新计算该系统的阶跃响应，结果为：
Gs=tf(10000,[1000 10050]);
Step(10*Gs)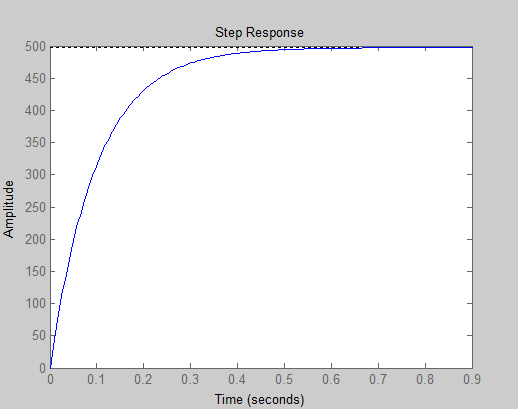 
此时系统的稳态误差接近为零，系统上升时间也降到了0.5s以下。这样做虽然满足了系统性能要求，但实际上该控制过程在现实中难以实现。因此，引入比例积分（PI）控制器来对系统进行调节。
（2）比例积分（PI）控制器的设计
采用比例积分控制的系统闭环传递函数可表示为：
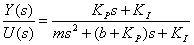
增加积分环节的目的是减小系统的稳态误差，假设比例系数Kp=600，积分系数KI=1，编写相应的MATLAB程序代码如下：
Gs=tf([600 1],[1000 650 1]);
Step(500*Gs)
运行上述程序后可得系统阶跃响应曲线为：
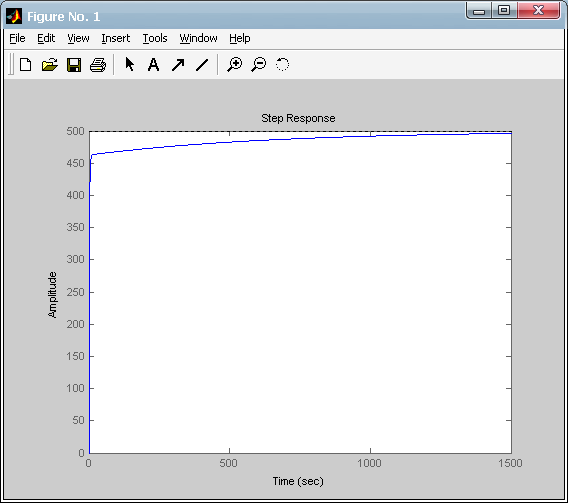
可以调节控制器的比例和积分系数来满足系统的性能要求。例如选择比例系数KP＝800，积分系数KI=40时，可得系统阶跃响应曲线为：
Gs=tf([800 40],[1000 850 40]);
Step(500*Gs)
可见，此时的控制系统已经能够满足系统要求达到的性能指标设计要求。但此控制器无微分项，而对于有些实际控制系统往往需要设计完整的PID控制器，以便同时满足系统的动态和稳态性能要求。
（3）比例积分微分（PID）控制器的设计
采用PID控制的系统闭环传递函数为：
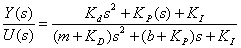
假设该控制器的比例系数KP=1，积分系数KI =1，微分系数KD=1，编写MATLAB程序代码如下：
Gs=tf([1 1 1],[1001 51 1]);
step(500*Gs)
运行上述程序，并且调整PID控制器的控制参数，直到控制器满足系统设计的性能指标要求为止。
最后，选择KP= 2000，KI = 700 ，KD= 1 ，此时系统的阶跃响应曲线如下：
从图中可以看出该系统能够满足设计的总体性能要求。
● 利用Simulink进行仿真设计
I．求系统的开环阶跃响应
利用Simulink建立系统阶跃响应模型，如下图所示。双击Step模块，设置模块属性：跳变时间为0；初始值为0；终止值为10；采样时间为0。
单击◢按钮开始仿真，双击Scope模块，可得系统阶跃响应曲线。
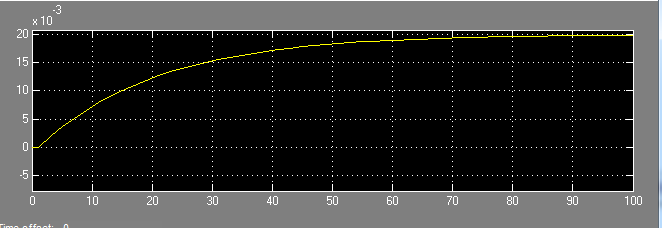
分析此时系统的性能指标是否满足设计要求？若不能则应加上合适的控制器。
II．PID控制器的设计
在Simulink的模型窗口建立一个包含PID控制器的闭环系统阶跃响应模型，如图所示：
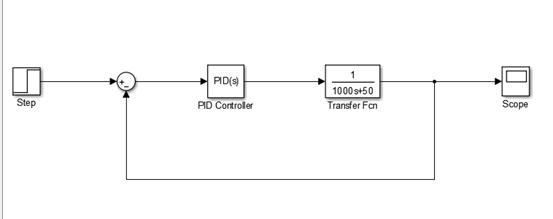
分别双击Kp、Ki、Kd模块设定比例、积分、微分系数，点击◢按钮开始仿真，双击Scope模块，观察系统的阶跃响应曲线，直到满足要求为止。
最终选取KP= 3000 ，KI= 800 ，KD= 1 ，此时控制器能满足系统设计所要求达到的性能指标，Simulink仿真的汽车运动PID控制系统的阶跃响应曲线如下：
六．总结与体会
实验总结：
（总结实验中遇到的问题及解决办法，分析PID控制器三种控制所起的作用等。）
在实验中遇倒最大的问题就是如何快速地找到使系统满足要求的pid参数。
其中：p为比例系数，与系统的增益有关，p越大增益作用越大。初调时，应选小一些，然后慢慢调大，直到系统波动足够小。
I为微分系数，微分值是偏差值的变化率。当系统的时间滞后时，可附加该参数。
D为积分系数，积分时间常数的定义是，偏差引起输出增长的时间。初调时要把积分时间设置长些，然后慢慢调小直到系统稳定为止。
通过不断的调节其参数以达到最终的目的。