
系统仿真实验报告
班 级:电气工程及其自动化1301班
学 号:
姓 名:
指导老师:
完成时间:20##年4月19日
目 录
实验一 MATLAB中矩阵与多项式的基本运算.................................................................. - 1 -
实验二 MATLAB绘图命令....................................................................................................... 8
实验三 MATLAB程序设计..................................................................................................... 10
实验四 MATLAB的符号计算与SIMULINK的使用........................................................... 11
实验五 MATLAB在控制系统分析中的应用......................................................................... 13
实验六 连续系统数字仿真的基本算法.................................................................................. 22
实验一 MATLAB中矩阵与多项式的基本运算
实验任务
1.了解MATLAB命令窗口和程序文件的调用。
2.熟悉如下MATLAB的基本运算:
① 矩阵的产生、数据的输入、相关元素的显示;
② 矩阵的加法、乘法、左除、右除;
③ 特殊矩阵:单位矩阵、“1”矩阵、“0”矩阵、对角阵、随机矩阵的产生和运算;
④ 多项式的运算:多项式求根、多项式之间的乘除。
【命令】与【运行结果】
>> eye(3)
ans =
1 0 0
0 1 0
0 0 1
>> ones(3)
ans =
1 1 1
1 1 1
1 1 1
>> zeros(3,4)
ans =
0 0 0 0
0 0 0 0
0 0 0 0
>> rand(3,4)
ans =
0.8147 0.9134 0.2785 0.9649
0.9058 0.6324 0.5469 0.1576
0.1270 0.0975 0.9575 0.9706
>> diag(3)
ans =
3
>> A=rand(3),diag(A)
A =
0.9572 0.1419 0.7922
0.4854 0.4218 0.9595
0.8003 0.9157 0.6557
ans =
0.9572
0.4218
0.6557
>> A=[1 2 3;4 5 6;7 8 9];...
B=[1 3 5;7 9 2;4 6 8];...
A\B,B/A,inv(A)*B ,B*inv(A),inv(B)*A
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.541976e-018.
ans =
1.0e+016 *
4.0532 4.0532 -4.0532
-8.1065 -8.1065 8.1065
4.0532 4.0532 -4.0532
Warning: Matrix is singular to working precision.
ans =
NaN -Inf Inf
NaN -Inf Inf
NaN -Inf Inf
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.541976e-018.
ans =
1.0e+016 *
4.0532 4.0532 -4.0532
-8.1065 -8.1065 8.1065
4.0532 4.0532 -4.0532
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.541976e-018.
ans =
1.0e+016 *
0.0000 0 0
4.0532 -8.1065 4.0532
0 0 0
ans =
3.5000 3.0000 2.5000
-2.5000 -2.0000 -1.5000
1.0000 1.0000 1.0000
【结果分析】
题目中的矩阵A是没有逆的,但由于计算机精度的问题,使得上面的结果比较奇怪:
首先,B/A应该和B*inv(A)都出错显示结果为无定义,但是事实上却是前者结果无定义,而后者却又结果。另外A\B和inv(A)*B 应该也是没有定义的,但还是有结果,因此,我们有必要检查运算结果,鉴于软件在精度方面不可避免的误差。
>>syms x
f=3*x^5+4*x^3-5*x^2-7*x+5;
p=[3,0,4,-5,-7,5];
X=roots(p)
poly(X)
X =
-0.3074 + 1.6176i
-0.3074 - 1.6176i
-1.0000
1.0000
0.6147
ans =
1.0000 0.0000 1.3333 -1.6667 -2.3333 1.6667
>> A=fix(10*rand(1,3)),B=fix(20*rand(1,4))
conv(A,B),[Q,r]=deconv(B,A)
A =
6 1 1
B =
9 19 6 11
ans =
54 123 64 91 17 11
Q =
1.5000 2.9167
r =
0 0 1.5833 8.0833
>> A=fix(10*rand(3)),B=fix(20*rand(3))
A*B,A.*B
A =
2 3 5
6 8 9
4 5 2
B =
15 11 10
15 1 15
7 1 18
ans =
110 30 155
273 83 342
149 51 151
ans =
30 33 50
90 8 135
28 5 36
【结果分析】:A*B是正常的规矩乘法,而A.*B是一种扩展功能,其结果Cij=Aij*Bij。
>> who
Your variables are:
A B Q X ans f p r x
>> whos
Name Size Bytes Class Attributes
A 3x3 72 double
B 3x3 72 double
Q 1x2 16 double
X 5x1 80 double complex
ans 3x3 72 double
f 1x1 170 sym
p 1x6 48 double
r 1x4 32 double
x 1x1 126 sym
>> A=fix(10*rand(1,3)),B=fix(20*rand(3)),C=fix(10*rand(3,2)),D=[3]
diag(A),diag(B),diag(C),diag(D)
A =
8 0 3
B =
5 18 2
16 3 2
8 5 17
C =
5 8
5 6
1 3
D =
3
ans =
8 0 0
0 0 0
0 0 3
ans =
5
3
17
ans =
5
6
ans =
3
>> disp('lalalalaalalllallla');
A=fix(10*rand(3,2)),B=zeros(3),C=ones(3,6)
size(A),length(A),size(B),length(B),size(C),length(C)
lalalalaalalllallla
A =
2 9
4 9
0 4
B =
0 0 0
0 0 0
0 0 0
C =
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
ans =3 2
ans =3
ans =3 3
ans =3
ans =3 6
ans =6
【结果分析】:disp不受”;分号”影响,size输出矩阵的行数和列数,length输出行列数较大值
实验二 MATLAB绘图命令
实验任务
熟悉MATLAB基本绘图命令,掌握如下绘图方法:
1.坐标系的选择、图形的绘制;
2.图形注解(题目、标号、说明、分格线)的加入;
3.图形线型、符号、颜色的选取。
【程序】
x=linspace(0,100,pi);
y1=x.*x;
y2=x.*x.*x;
subplot(2,2,1);plot(x,y1,'-.b',x,y2,'r'),legend('y=x^{2}','y=x^{3}'); grid off;
subplot(2,2,2);loglog(x,y1,'rp-',x,y2,':b'),title('说啥好呢'),grid on;
subplot(2,2,3);semilogx(x,y1,'b*-',x,y2,'r+-'),xlabel('X'),ylabel('Y');
subplot(2,2,4);semilogy(x,y1,'g-+',x,y2,'m'),text(50,8000,'y=x^{2}'),
text(40,100000,'y=x^{3}')
【结果截图】
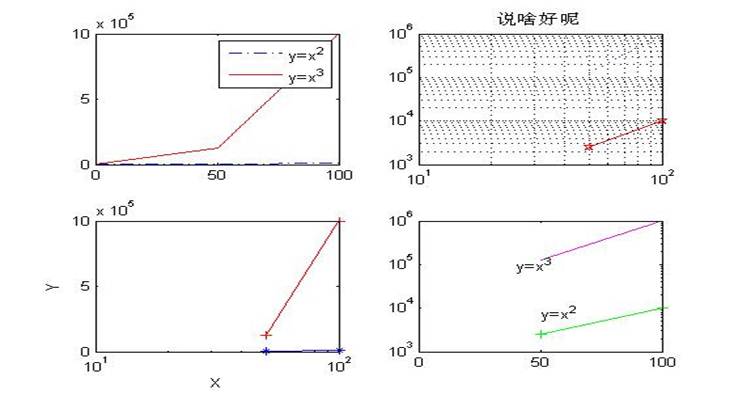 【程序】
【程序】
t=0:0.01:2*pi;
r=sin(2*t).*cos(2*t);
subplot(2,2,1);polar(t,r)
subplot(2,2,2);bar(t,r,'r'),axis([0,1,-0.5,0.5]),title('bar')
subplot(2,1,2);stairs(t,r,'c'),axis([0,1,-0.5,0.5]),title('stairs')
【结果截图】

【程序】
[x,y,z]=peaks(100);
subplot(1,2,1),mesh(x,y,z)
subplot(1,2,2),contour(x,y,z)
【结果截图】

实验三 MATLAB程序设计
实验任务
用一个MATLAB语言编写一个程序:输入一个自然数,判断它是否是素数,如果是,输出“It is one prime”,如果不是,输出“It is not one prime.”。要求通过调用子函数实现。最好能具有如下功能:①设计较好的人机对话界面,程序中含有提示性的输入输出语句。②能实现循环操作,由操作者输入相关命令来控制是否继续进行素数的判断。如果操作者希望停止这种判断,则可以退出程序。③如果所输入的自然数是一个合数,除了给出其不是素数的结论外,还应给出至少一种其因数分解形式。例:输入 6, 因为6不是素数。则程序中除了有“It is not one prime”的结论外,还应有:“6=2*3”的说明。
【程序】:
a=input('请输入一个整数(end in 0):');
while(a~=0)
if a==1
disp('1 is not a prime or a composite number.')
elseif isprime(a)==1
fprintf('%d is a prime.\n',a)
elseif isprime(a)==0
f=factor(a);m=length(f);
fprintf('%d is not a prime,%d=%d',a,a,f(1))
for i=2:m
fprintf('*%d',f(i));
end
fprintf('\n');
end
a=input('请输入一个整数(end in 0):');
end
【运行结果】:
请输入一个整数(end in 0):1
1 is not a prime or a composite number.
请输入一个整数(end in 0):2
2 is a prime.
请输入一个整数(end in 0):35
35 is not a prime,35=5*7
请输入一个整数(end in 0):0
>>
实验四 MATLAB的符号计算与SIMULINK的使用
实验任务
1.掌握MATLAB符号计算的特点和常用基本命令;
2.掌握SIMULINK的使用。
【程序1】
syms a b c d
A=[a b;c d];B=[1,4;2,9]; det(A),det(B),eig(A),eig(B)
【运行结果1】
ans = a*d-b*c
ans = 1
ans = 1/2*a+1/2*d+1/2*(a^2-2*a*d+d^2+4*b*c)^(1/2)
1/2*a+1/2*d-1/2*(a^2-2*a*d+d^2+4*b*c)^(1/2)
ans = 0.1010
9.8990
【程序2】
r=solve('x^3+5*x^2-9*x+17')
r4=vpa(r,4)
r10=vpa(r,10)
【运行结果2】
r =
-1/3*(557+3*18849^(1/2))^(1/3)-52/3/(557+3*18849^(1/2))^(1/3)-5/3
1/6*(557+3*18849^(1/2))^(1/3)+26/3/(557+3*18849^(1/2))^(1/3)-5/3+1/2*i*3^(1/2)*(-1/3*(557+3*18849^(1/2))^(1/3)+52/3/(557+3*18849^(1/2))^(1/3))
1/6*(557+3*18849^(1/2))^(1/3)+26/3/(557+3*18849^(1/2))^(1/3)-5/3-1/2*i*3^(1/2)*(-1/3*(557+3*18849^(1/2))^(1/3)+52/3/(557+3*18849^(1/2))^(1/3))
r4 =
-6.717
.858-1.339*i
.858+1.339*i
r10 =
-6.716750613
.858375306-1.339469138*i
.858375306+1.339469138*i
【simulink仿真】
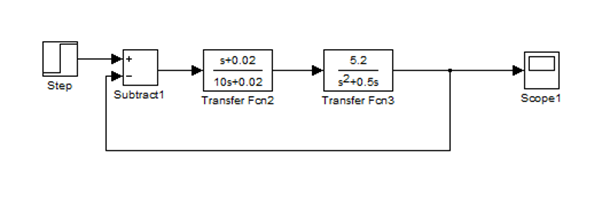 【仿真结果】
【仿真结果】
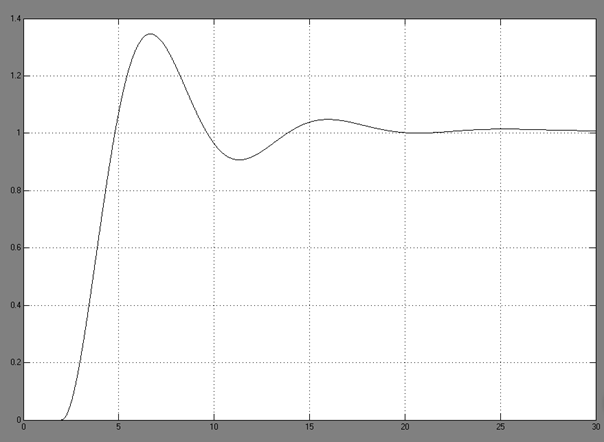
实验五 MATLAB在控制系统分析中的应用
一、实验任务
1.掌握MATLAB在控制系统时间响应分析中的应用;
2.掌握MATLAB在系统根轨迹分析中的应用;
3. 掌握MATLAB控制系统频率分析中的应用;
4. 掌握MATLAB在控制系统稳定性分析中的应用
1. 求下面系统的单位阶跃响应
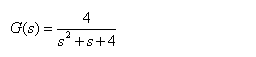
【程序】
num=[4] ; den=[1 , 1 , 4] ;step(num , den)
[y , x , t]=step(num , den) ;
 tp=spline(y , t , max(y)) %计算峰值时间
tp=spline(y , t , max(y)) %计算峰值时间
ymaxmax(y) %计算峰值
【结果】
tp =1.5708
ymax =1.4419
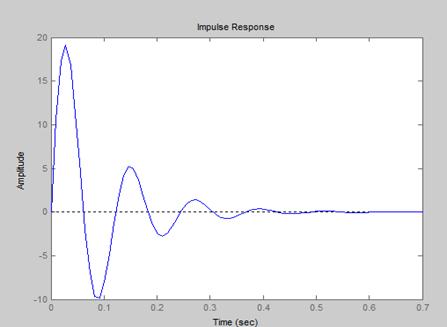
2. 求下面系统的单位脉冲响应:
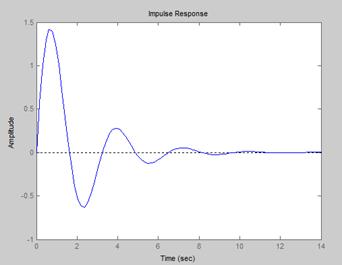

【程序】
num=[4] ; den=[1 , 1 ,4] ;
impulse(num,den)
【结果如右图】
3.已知二阶系统的状态方程为:
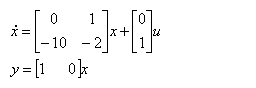
求系统的零输入响应和脉冲响应。
【程序如下】: 【结果如下图】
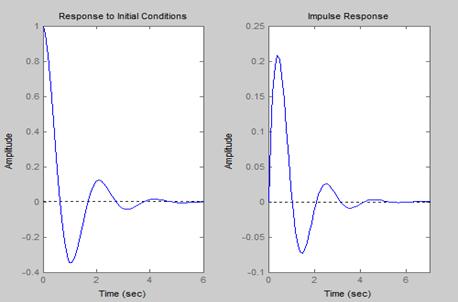 a=[0 , 1 ; -10 , -2] ;
a=[0 , 1 ; -10 , -2] ;
b=[0 ; 1] ;
c=[1 , 0] ;
d=[0] ;
x0=[1 ,0];
subplot(1 , 2 , 1) ;
initial(a , b , c ,d,x0)
subplot(1 , 2 , 2) ;
impulse(a , b , c , d)
4.系统传递函数为:

输入正弦信号时,观察输出信号的相位差。
【程序如下】: 【结果如下图】:
 num=[1] ; den=[1 , 1] ;
num=[1] ; den=[1 , 1] ;
t=0 : 0.01 : 10 ;
u=sin(2*t) ;
hold on
plot(t , u , ‘r’)
lsim(num , den , u , t)
5.有一二阶系统,求出周期为4秒的方波的输出响应
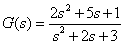
【程序如下】: 【结果如下图】:
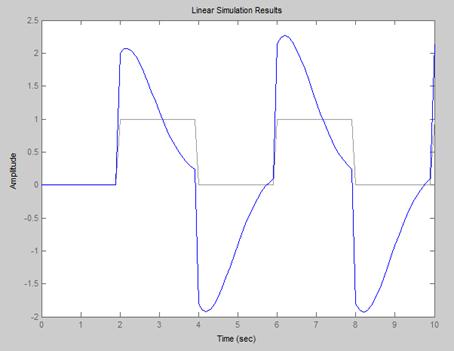 num=[2 5 1];
num=[2 5 1];
den=[1 2 3];
t=(0:.1:10);
period=4;
u=(rem(t,period)>=period./2);
lsim(num,den,u,t);
6.已知开环系统传递函数,绘制系统的根轨迹,并分析其稳定性
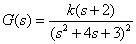
【程序如下】:
num=[1 2];den1=[1 4 3];den=conv(den1,den1);figure(1)
rlocus(num,den)
[k,p]= rlocfind(num,den)
figure(2)
k=55;num1=k*[1 2];den=[1 4 3];den1=conv(den,den);[num,den]=cloop(num1,den1,-1);
impulse(num,den)
title('impulse response (k=55) ')
figure(3)
k=56;num1=k*[1 2];den=[1 4 3];den1=conv(den,den);[num,den]=cloop(num1,den1,-1);
impulse(num,den)
title('impulse response(k=56)')
【结果】:
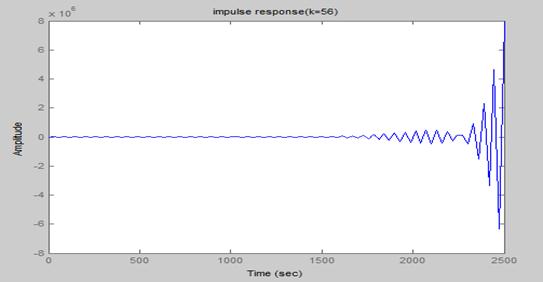
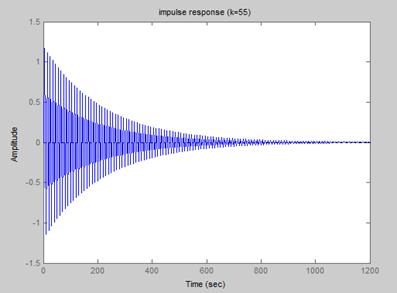

K=55时系统稳定,k=56时系统发散。
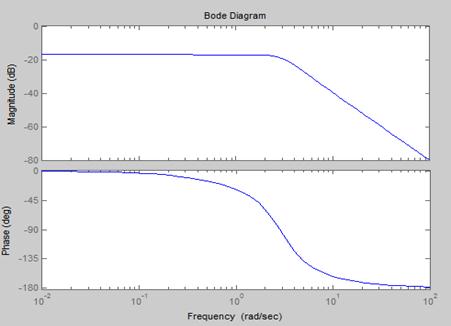
7. 作如下系统的bode图
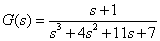
【程序如下】: 【结果】:
 n=[1 , 1] ;
n=[1 , 1] ;
d=[1 , 4 , 11 , 7] ;
bode(n , d)
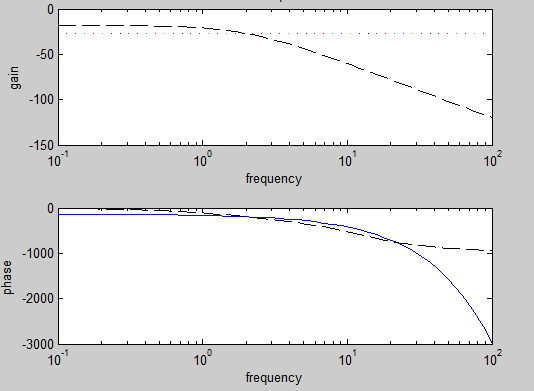
8.系统传函如下
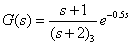
求有理传函的频率响应,然后在同一张图上绘出以四阶伯德近似表示的系统频率响应
【程序如下】:
num=[1];den=conv([1 2],conv([1 2],[1 2]));
w=logspace(-1,2); t=0.5;
[m1,p1]=bode(num,den,2);
p1=p1-t*w'*180/pi; [n2,d2]=pade(t,4);
numt=conv(n2,num);dent=(conv(den,d2));
[m2,p2]=bode(numt,dent,w);
subplot(2,1,1);
semilogx(w,20*log10(m1),w,20*log10(m2),'k--');
title('bode plot');xlabel('frequency');ylabel('gain');
subplot(2,1,2);
semilogx(w,p1,w,p2,'k--');
xlabel('frequency');ylabel('phase');
【结果如下图】:
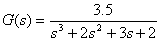 9.已知系统模型为
9.已知系统模型为
求它的幅值裕度和相角裕度
【程序如下】:
n=[3.5]; d=[1 2 3 2];
[Gm,Pm,Wcg,Wcp]=margin(n,d)
【结果】:
Gm =1.1433
Pm =7.1688
Wcg =1.7323
Wcp =1.6541
10.二阶系统为:
令wn=1,分别作出ξ=2 , 1 , 0.707 , 0.5时的nyquist曲线。
【程序如下】:
n=[1] ;
d1=[1 , 4 , 1] ; d2=[1 , 2 , 1] ; d3=[1 , 1.414 , 1]; d4=[1,1,1];
nyquist(n,d1) ;
hold on
nyquist(n,d2) ; nyquist(n,d3) ; nyquist(n,d4) ;
【结果如下图】:

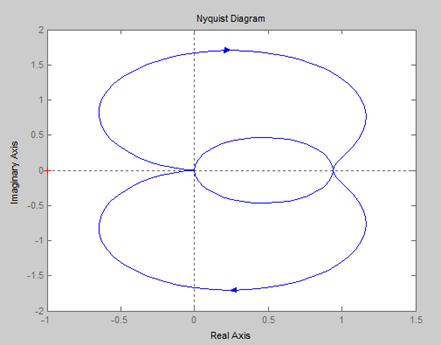
11.一多环系统,其结构图如下,使用Nyquist频率曲线判断系统的稳定性。
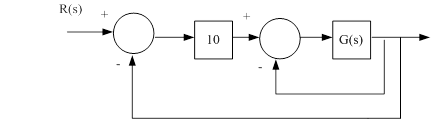
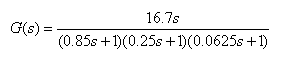
【程序如下】:
k1=16.7/0.0125;z1=[0]; p1=[-1.25 -4 -16]; [num1,den1]=zp2tf(z1,p1,k1);
[num,den]=cloop(num1,den1); [z,p,k]=tf2zp(num,den);
figure(1)
nyquist(num,den)
figure(2)
[num2,den2]=cloop(num,den); impulse(num2,den2);
【结果如下图】:
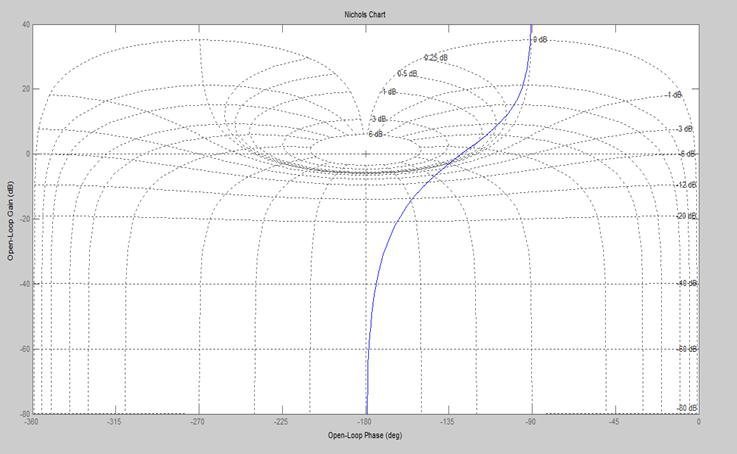
 12. 已知系统为:
12. 已知系统为:
作该系统的nichols曲线。
【程序如下】:
n=[1] ; d=[1 , 1 , 0] ; ngrid(‘new’) ; nichols(n , d) ;
【结果如下图】:
实验六 连续系统数字仿真的基本算法
实验任务
1.理解欧拉法和龙格-库塔法的基本思想;
2.理解数值积分算法的计算精度、速度、稳定性与步长的关系;
1. 取h=0.2,试分别用欧拉法、RK2法和RK4法求解微分方程的数值解,并比较计算精度。
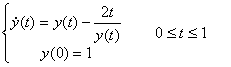
注:解析解: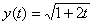
【程序】
clear
t(1)=0; % 置自变量初值
y(1)=1; y_euler(1)=1; y_rk2(1)=1; y_rk4(1)=1; % 置解析解和数值解的初值
h=0.2; % 步长
% 求解析解
for k=1:5
t(k+1)=t(k)+h;
y(k+1)=sqrt(1+2*t(k+1));
end
% 利用欧拉法求解
for k=1:5
y_euler(k+1)=y_euler(k)+h*(y_euler(k)-2*t(k)/y_euler(k));
end
% 利用RK2法求解
for k=1:5
k1=y_rk2(k)-2*t(k)/y_rk2(k);
k2=(y_rk2(k)+h*k1)-2*(t(k)+h)/(y_rk2(k)+h*k1);
y_rk2(k+1)=y_rk2(k)+h*(k1+k2)/2;
end
% 利用RK4法求解
for k=1:5
k1=y_rk4(k)-2*t(k)/y_rk4(k);
k2=(y_rk4(k)+h*k1/2)-2*(t(k)+h/2)/(y_rk4(k)+h*k1/2);
k3=(y_rk4(k)+h*k2/2)-2*(t(k)+h/2)/(y_rk4(k)+h*k2/2);
k4=(y_rk4(k)+h*k3)-2*(t(k)+h)/(y_rk4(k)+h*k3);
y_rk4(k+1)=y_rk4(k)+h*(k1+2*k2+2*k3+k4)/6;
end
disp(' 时间 解析解 欧拉法 RK2法 RK4法')
yt=[t', y', y_euler', y_rk2', y_rk4'];
disp(yt)
【运行结果】
时间 解析解 欧拉法 RK2法 RK4法
0 1.0000 1.0000 1.0000 1.0000
0.2000 1.1832 1.2000 1.1867 1.1832
0.4000 1.3416 1.3733 1.3483 1.3417
0.6000 1.4832 1.5315 1.4937 1.4833
0.8000 1.6125 1.6811 1.6279 1.6125
1.0000 1.7321 1.8269 1.7542 1.7321
%H=0.05
时间 解析解 欧拉法 RK2法 RK4法
0 1.0000 1.0000 1.0000 1.0000
0.0500 1.0488 1.0500 1.0489 1.0488
0.1000 1.0954 1.0977 1.0956 1.0954
0.1500 1.1402 1.1435 1.1403 1.1402
0.2000 1.1832 1.1876 1.1834 1.1832
0.2500 1.2247 1.2301 1.2250 1.2247
H=0.001
时间 解析解 欧拉法 RK2法 RK4法
0 1.0000 1.0000 1.0000 1.0000
0.0010 1.0010 1.0010 1.0010 1.0010
0.0020 1.0020 1.0020 1.0020 1.0020
0.0030 1.0030 1.0030 1.0030 1.0030
0.0040 1.0040 1.0040 1.0040 1.0040
0.0050 1.0050 1.0050 1.0050 1.0050
%欧拉法需要步长足够小时才逼近解析解,RK4逼近得最快,其次是RK2
2. 考虑如下二阶系统:
 在
在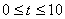 上的数字仿真解(已知:
上的数字仿真解(已知: ,
,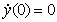 ),
),
并将不同步长下的仿真结果与解析解进行精度比较。
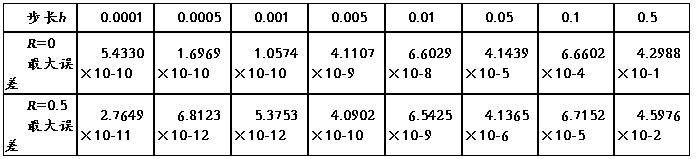
说明:
已知该微分方程的解析解分别为:

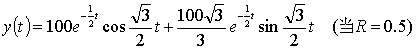
采用RK4法进行计算,选择状态变量:
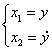
则有如下状态空间模型及初值条件
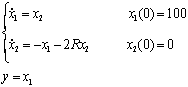
采用RK4法进行计算。程序如下:
clear
h=input('请输入步长h='); % 输入步长
M=round(10/h); % 置总计算步数
t(1)=0; % 置自变量初值
y_0(1)=100; y_05(1)=100; % 置解析解的初始值(y_0和y_05分别对应于为R=0和R=0.5)
x1(1)=100; x2(1)=0; % 置状态向量初值
y_rk4_0(1)=x1(1); y_rk4_05(1)=x1(1); % 置数值解的初值
% 求解析解
for k=1:M
t(k+1)=t(k)+h;
y_0(k+1)=100*cos(t(k+1));
y_05(k+1)=100*exp(-t(k+1)/2).*cos(sqrt(3)/2*t(k+1))+100*sqrt(3)/3*exp(-t(k+1)/2).*sin(sqrt(3)/2*t(k+1));
end
% 利用RK4法求解
% R=0
for k=1:M
k11=x2(k); k12=-x1(k);
k21=x2(k)+h*k12/2; k22=-(x1(k)+h*k11/2);
k31=x2(k)+h*k22/2; k32=-(x1(k)+h*k21/2);
k41=x2(k)+h*k32; k42=-(x1(k)+h*k31);
x1(k+1)=x1(k)+h*(k11+2*k21+2*k31+k41)/6;
x2(k+1)=x2(k)+h*(k12+2*k22+2*k32+k42)/6;
y_rk4_0(k+1)=x1(k+1);
end
% R=0.5
for k=1:M
k11=x2(k); k12=-x1(k)-x2(k);
k21=x2(k)+h*k12/2; k22=-(x1(k)+h*k11/2)-(x2(k)+h*k12/2);
k31=x2(k)+h*k22/2; k32=-(x1(k)+h*k21/2)-(x2(k)+h*k22/2);
k41=x2(k)+h*k32; k42=-(x1(k)+h*k31)-(x2(k)+h*k32);
x1(k+1)=x1(k)+h*(k11+2*k21+2*k31+k41)/6;
x2(k+1)=x2(k)+h*(k12+2*k22+2*k32+k42)/6;
y_rk4_05(k+1)=x1(k+1);
end
% 求出误差最大值
err_0=max(abs(y_0-y_rk4_0));
err_05=max(abs(y_05-y_rk4_05));
% 输出结果
disp('最大误差(R=0) 最大误差(R=0.5)')
err_max=[err_0,err_05];
disp(err_max)
步长h取0.0001 到0.5之间变化,并且将数值解直接与解析解比较,求出最大误差数据列入下表中。
从上表中可以看出,当步长h=0.001时,总误差最小;当步长h小于0.001时,由于舍入误差变大而使总误差增加;当步长h大于0.001时,则由于截断误差的增加也使得总误差加大。另外,当系统的解变化激烈时(如R=0),误差对步长的变化较为敏感;当系统的解变化平稳时,步长的变化对误差的影响就要缓和得多。数值积分算法确定以后,在选择步长时,需要综合考虑。
