宜宾学院数模竞赛论文模版:
宜宾学院第三届
大学生数学建模竞赛
(20##年5月19日-5月28日)
参赛题目(在所选题目上打勾) A B
参赛编号(竞赛组委会填写)

评阅记录(竞赛评审委员会评阅时使用):

论文题目
摘 要
1、摘要:本文解决什么问题,解决问题的方法,结论.
提请大家注意:摘要应该是一份简明扼要的详细摘要(包括关键词),在整篇论文评阅中占有重要权重,请认真书写(注意篇幅不能超过一页,且无需译成英文)。
关键词:
2、正文
一、问题的提出:叙述问题内容及意义.
二、基本假设:写出问题的合理假设.
三、建立模型:详细叙述模型、变量、参数代表的意义和满足的条件及建模思想.
四、模型求解:求解、算法的主要步骤.
五、结果分析与检验:(含误差分析).
六、模型评价:优缺点及改进意见.
七、参考文献:限公开发表文献,指明出处..
3、附件:计算框图、程序及打印结果.
参考文献 例子
[1]吕显瑞等. 数学建模竞赛辅导教材[M]. 长春: 吉林大学出版社, 2002: 56-98
[2]刘来福,曾文艺. 数学模型与数学建模[M]. 北京: 北京师范大学出版社, 1997: 78-89
[3]熊慧. 论人口预测对上海市未来十年人口总数的预测. 人口研究[J], 2003, 28(1): 88-90
[4]20##年国民经济和社会发展统计公报, Http://www.stats.gov.cn, 20##年9月20日

范文:
基于双种群遗传算法的公交路线查询问题
摘 要
本文探讨的是公交路线选择而开发的查询系统.以两站点之间所花时间的最小值作为主要目标函数,利用双种群遗传算法的原理建立公交路线选择数学模型,再通过MATLAB程序来实现整个流程和迭代,最终求出全局近似最优解,即最优权重线路,以起点和终点查询到近似的最优公交路线,并进行了误差分析,模型的评价与推广.
问题一:仅考虑公汽线路,对数据进行初步分析和处理后,考虑到数据的复杂性和数据搜索范围的广度,我们应用比较成熟的双种群遗传算法建立数学模型. 通过MATLAB强大的矩阵运算功能得到站点之间的邻接矩阵,用时间加权. 其流程思想为基于双种群初始群体A、B,对染色体进行整数编码,用竞争选择法选择出较优个体作为繁殖下一代的母体,依据选择性集成思想,等概率使用两点交叉法和区域交叉法对染色体进行交叉操作与使用邻居交换变异和两点交换变异进行染色体变异操作,并结合MATLAB反复迭代,最终给出了六对起始站与终点站的六条近似最优路线. 该法扩大遗传算法的搜索范围,避免过早收敛.
问题二:在数据处理上用时间加权把地铁站点和汽车站点统一化,可得所有站点之间的邻接矩阵. 其求解原理与问题一相似,但由转车方式的不同生成了8种不同的适应度函数,再根据适应度函数来进行问题的求解.
问题三:我们将任意两个站点之间的步行时间作为矩阵中相应位置的权,这时构建的邻接矩阵中的权就由两站点之间公汽到公汽的时间,公汽到地铁的时间,地铁到公汽的时间,地铁到地铁的时间和两点之间的步行时间构成. 但其求解原理与问题一相似,但由转车方式的不同就会生成不同的适应度函数,再根据适应度函数来进行问题的求解.
双种群遗传算法提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对问题的种类有很强的鲁棒性,具有自组织、自适应和自学习性.
关键词:双种群遗传算法;竞争选择法;离散赌轮选择算子;选择性集成思想
一、问题的重述
第29届奥运会明年8月将在北京举行,届时有大量观众到现场观看奥运比赛,其中大部分人将会乘坐公共交通工具(简称公汽,包括公汽、地铁等)出行. 北京市的公汽线路已达800条以上,使得公众的出行更加通畅、便利,但同时也面临多条线路的选择问题. 针对市场需求,某公司准备研制开发一个解决公汽线路选择问题的自主查询计算机系统.
为了设计这样一个系统(核心是线路选择的模型与算法),从实际情况出发,满足查询者的各种不同需求. 需要研究的问题如下:
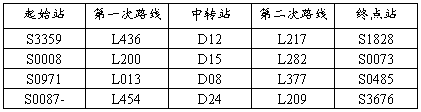
问题一:只考虑公汽线路情况,给出任意两公汽站点之间线路选择问题的一般数学模型与算法. 并根据基本参数设定中的数据,利用其模型与算法,求出6对起始站→终到站之间的最佳路线,并要有清晰的评价说明. 见下表:

问题二:同时考虑公汽与地铁线路,解决以上问题.
问题三:假设知道所有站点之间的步行时间,给出任意两站点之间线路选择问题的数学模型.
其中基本参数设定:
相邻公汽站平均行驶时间(包括停站时间):3分钟
相邻地铁站平均行驶时间(包括停站时间):2.5分钟
公汽换乘公汽平均耗时:5分钟(其中步行时间2分钟)
地铁换乘地铁平均耗时:4分钟(其中步行时间2分钟)
地铁换乘公汽平均耗时:7分钟(其中步行时间4分钟)
公汽换乘地铁平均耗时:6分钟(其中步行时间4分钟)
公汽票价:分为单一票价与分段计价两种,标记于线路后;其中分段计
价的票价为:0~20站:1元;21~40站:2元;40站以上:3元
地铁票价:3元(无论地铁线路间是否换乘)
注:以上参数均为简化问题而作的假设,未必与实际数据完全吻合.
公汽线路及相关信息见数据文件B2007data.rar.
二、模型的假设
1. 转车的次数控制在2次以内;
2. 相邻公汽站平均行驶时间(包括停站时间):3分钟;
3. 相邻地铁站平均行驶时间(包括停站时间):2.5分钟;
4. 公汽换乘公汽平均耗时:5分钟(其中步行时间2分钟);
5. 地铁换乘地铁平均耗时:4分钟(其中步行时间2分钟);
6. 地铁换乘公汽平均耗时:7分钟(其中步行时间4分钟);
7. 公汽换乘地铁平均耗时:6分钟(其中步行时间4分钟);
8. 公汽票价:分为单一票价与分段计价两种,标记于线路后,其中分段计
价的票价为:0~20站:1元,21~40站:2元,40站以上:3元;
9. 地铁票价:3元(无论地铁线路间是否换乘);
10. 知道所有站点之间的步行时间.
三、符号说明
C:只考虑公汽线路的情况下,每个个体对应路线总长;
D:考虑公汽和地铁线路的情况下,每个个体对应路线部长;
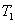 :相邻公汽站平均行驶时间(包括停站时间);
:相邻公汽站平均行驶时间(包括停站时间);
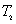 :相邻地铁站平均行驶时间(包括停站时间);
:相邻地铁站平均行驶时间(包括停站时间);
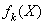 :第k个个体所对应的适应度值;
:第k个个体所对应的适应度值;
A:每个个体所对应的适应度比例;
P:每个个体所对应的选择概率(适应度比例);
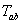 :所有站点之间的步行时间;
:所有站点之间的步行时间;
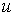 :表示转车换乘所耗时间之和.
:表示转车换乘所耗时间之和.
四、模型的建立与求解
(一)问题一
1.1 问题分析
该问题是一个组合优化问题. 对于此类问题,只有当其规模较小时,才能求其精确解. 在本文中公汽路线总数与站点数是成指数型增长的,所以一般很难精确地求出其最优解,因而寻找出有效的近似求解算法就具有重要意义.
由于L406公汽线路的路线是环形的,而数据中没有标示出来,所以我们用相邻站点整体路线也相邻,判断出该公汽线路是环行的,所以应当作环行处理. 对于该问题,我们先求出其站点与站点之间的邻接矩阵(权用时间表示),其矩阵大小为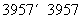 ,数据量太多,不能输出,只能把放在内存中.
,数据量太多,不能输出,只能把放在内存中.
许多智能算法被用于求解两点间线路问题. 如禁忌搜索、模拟退火、蚁群算法等. 其中遗传算法是被研究最多的一种算法. 但标准遗传算法容易陷入局部极值解,出现“早熟收敛”现象. 为此人们提出了多种改进方法,如将遗传算子中的交叉算子进行改进,应用单亲遗传算法,将遗传算子与启发式算法结合等.
遗传算法的核心思想为自然选择,适者生存. 遗传算法作为一种模拟生物进化的一种算法,提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对问题的种类有很强的鲁棒性,具有自组织、自适应和自学习性. 其也是一种迭代算法,从选定的初始解出发,通过不断地迭代,逐步改进当前解,直到最后搜索到最优解或满意解,其迭代过程是从一组初始解(群体)出发,采用类似于自然选择和有性繁殖的方法,在继承原有优良基因的基础上生成具有更好性能的下一代解的群体. 遗传算法的流程图见下图:
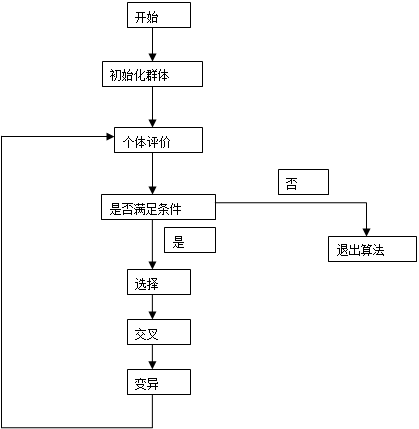
遗传算法流程图
标准遗传算法是针对一个宏观的种群进行选择、交叉、变异三种操作.
双种群遗传算法是一种并行遗传算法,它使用多种群同时进化,并交换种群之间优秀个体所携带的遗传信息,以打破种群内的平衡态达到更高的平衡态,跳出局部最优. 在双种群遗传算法中,每一种群都是按照标准算法进行操作. 在操作时,首先建立两个遗传算法群体,即种群A和种群B,分别独立地进行选择、交叉、变异操作,且交叉概率、变异概率不同. 当每一代运行结束以后,产生一个随机数n,分别从A,B中选出最优染色体和n个染色体进行杂交,以打破平衡态. 因为在双种群遗传算法中,每一种群都是按照标准算法进行操作的.
由上分析,对于本问题,我们釆用双种群遗传 (double populations genetic algorithm)在选择公汽路线问题中的应用.
(double populations genetic algorithm)在选择公汽路线问题中的应用.
遗传算法的创始人美国著名学者、密西根大学教授John H.Holland认为,可以用一组编码来模拟一组计算机程序,并且定义了一个衡量每个“程序”的度量:“适应值”. Holland模拟自然选择机制对这组“程序”进行“进化”,直到最终得到一个正确的“程序”为止. 编码方式有:二进制编码、十进制编码和符号编码等方法. 整数编码与符号编码一般用于与顺序有关的组合优化方面的问题. 根据公汽路线的特点,本文的工作采用整数 . 染色体长度与公汽路线结点个数相同,染色体的每个基因的编码即为公汽路线结点的编号. 因此,每条染色体由1到n(3957)的一个全排列组成.
. 染色体长度与公汽路线结点个数相同,染色体的每个基因的编码即为公汽路线结点的编号. 因此,每条染色体由1到n(3957)的一个全排列组成.
在对染色体进行 时,考虑到适应度比例法(轮盘赌选择法)与最佳个体保留法各自的优缺点,差异性较大,依据选择性集成思想,表现好的个体学习器越精确、差异越大,集成后可以获得的结果越好. 而竞争选择法集成了上述两种的优点克服了它们的缺点,因此本文釆用竞争选择法. 其中竞争选择法是釆用适应度比例法进行选择,交叉后产生下一代,再利用最佳个体保留法将上一代的最佳个体直接保存下来,然后从新群体中淘汰一个适应度最差的个体,提高了问题求解的收敛速度,体现了遗传算法自适应环境的能力.
时,考虑到适应度比例法(轮盘赌选择法)与最佳个体保留法各自的优缺点,差异性较大,依据选择性集成思想,表现好的个体学习器越精确、差异越大,集成后可以获得的结果越好. 而竞争选择法集成了上述两种的优点克服了它们的缺点,因此本文釆用竞争选择法. 其中竞争选择法是釆用适应度比例法进行选择,交叉后产生下一代,再利用最佳个体保留法将上一代的最佳个体直接保存下来,然后从新群体中淘汰一个适应度最差的个体,提高了问题求解的收敛速度,体现了遗传算法自适应环境的能力.
在对染色体进行交叉 时,对于由整数编码的染色体,交叉操作会形成染色体中的非法基因,即重复基因. 所以实现染色体交叉要将重复的基因清除. 只使用一种交叉方法容易引起过早收敛,即“早熟”. 依据选择性集成思想 ,等概率使用两点交叉法和区域交叉法这两种交叉方法,扩大遗传算法的搜索范围,避免过早收敛.
时,对于由整数编码的染色体,交叉操作会形成染色体中的非法基因,即重复基因. 所以实现染色体交叉要将重复的基因清除. 只使用一种交叉方法容易引起过早收敛,即“早熟”. 依据选择性集成思想 ,等概率使用两点交叉法和区域交叉法这两种交叉方法,扩大遗传算法的搜索范围,避免过早收敛.
在染色体的变异 中,与交叉方法一样,如果使用一种变异方法,同样可能会引起“早熟”. 为了避免过早收敛,依据选择性集成思想选择邻居交换变异和两点交换变异这两种个性好且差异性较大的变异方法,等概率使用以扩大搜索范围.
中,与交叉方法一样,如果使用一种变异方法,同样可能会引起“早熟”. 为了避免过早收敛,依据选择性集成思想选择邻居交换变异和两点交换变异这两种个性好且差异性较大的变异方法,等概率使用以扩大搜索范围.
1.2 模型建立
1.2.1 从起点站到终点站不转车,则双种群遗传算法的流程如下:
(1)产生邻接矩阵
邻接矩阵的MATLAB程序实现见附件一.
(2)基于站点序号的编码
一般来说种群规模越大越容易收敛到最优解,但是要保证其初始种群中的每个个体都是互异的,m不能设置过大,否则无法产生初始种群,且m过大其收敛速度必然降低,也会消耗更多的计算资源,并基于一般遗传算法中初始群体大小的选择,本文中取m=30.
公汽路线问题中每一种起点站到终点站的方案对应于解空间的一个解 ,解空间中的数据是遗传算法的表现形式,从表现到基因型的映射称为编码. 最初遗传算法是采用二进制编码方法,但在大量实际问题中,二进制编码操作不简便,不易进行变异交叉操作,易产生大量非可行解,所以针对特殊的问题,可以灵活采用不同的编码方法. 本文在公汽线路求解中,采用基于站点序号的实数编码,将染色体定义为公汽线路的一条解路线中的站点号序列,在MATLAB中为一个没有重复数字的行向量来表示. 设有n个站点的某个全排列为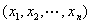 ,则个体的染色体表示为
,则个体的染色体表示为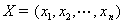 ,n=3957.
,n=3957.
(3)产生初始群体
种群中每一个体为n(3957)个站点的一个全排列,随机生成m(m=30)个1~n 的随机排列,得到m个个体的初始种群,m为种群大小,n为染色体长度.
生成初始群体的具体算法的MATLAB程序实现见附件二.
A、B初始群体的数据矩阵为 ,由于数据太多,文中就不给出数据(其结果可运行程序得出).
,由于数据太多,文中就不给出数据(其结果可运行程序得出).
(4)适应度函数与染色体的选择
在遗传算法进行搜索时只以适应度函数为依据,利用种群中个体每个的适应度值来进行搜索,适应度值是进化时优胜劣汰的依据,应用中总是根据问题的优化指标来定义.
对于公汽线路问题,以个体对应路线所发的时间之和作为个体适应度,其适应度越小,表明该个体越优. 则该个体对应 为:
为:
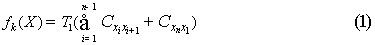
其中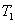 (3(分钟))表示相邻公汽站平均行驶时间(包括停站时间),
(3(分钟))表示相邻公汽站平均行驶时间(包括停站时间),
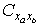 表示站点
表示站点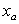 和
和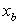 之间的距离,
之间的距离,
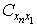 表示起始点与终点站之间的距离.
表示起始点与终点站之间的距离.
一般来说,选择算子设计使得个体被选中并遗传到下一代群体中的概率与该个体的适应度大小有关. 适应度是越高越好,而在公汽线路问题中,如果适应度是所经过的对应路线所花的时间之和,路线所花时间之和是越小越好,为了使公汽线路问题的适应度与一般遗传算法中的适应度一致. 这里用选择概率来进行衡量. 则每个个体的选择概率(适应度比例)就是每个个体的适应度与所有个体适应度的总和之比,即:

其中 表示所有个体适应度的总和.
表示所有个体适应度的总和.
但当路径所花时间非常大(例如:10000),这样其适应度比例的最高数据位将在小数点后的第四位,这样不利于计算,为此要进行尺度变换. 为确保适应度有两位整数,此处将适应度放大倍数L(本题中 L=lOOO) 因此适应度比例 的表达式为:
的表达式为:

遗传算法中选择算子设计经典的是用适应度成比例的概率方法 ,但是这里存在的问题是由于许多个体的适应度比例很小几乎没有机会复制个体,从而被过早地淘汰. 这样整个群体多样性就无法得到保证,这里采用一种新的赌轮选择算子——离散赌轮选择 ,将有效地避免了这个问题.
,将有效地避免了这个问题.
在本题中是由30个个体构成初始群体,即: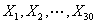 ,其所占的适应度比例分别是
,其所占的适应度比例分别是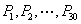 ,在保持这个比例的情况下对这个取值范围放大1000倍.
,在保持这个比例的情况下对这个取值范围放大1000倍.
按照顺序在1~1000内分别占不同的区间,当随机函数产生1~1000以内的时,即使是适应度比例最小的也有可能被选中,从而较好的保持了群体的多样性.
由上所述则可选择出适应力强的,淘汰适应力弱的个体从而得到总体适应能力强的群体.
经过选择算子得出总体适应能力强的A、B群体数据矩阵为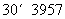 ,因数据量太大,文中就不给出具体数据.
,因数据量太大,文中就不给出具体数据.
(5)交叉重组
依据选择性集成思想 ,等概率使用两点交叉法和区域交叉法这两种差异性较大的交叉方法,扩大遗传算法的搜索范围,避免过早收敛.
其中,两点交叉法是先随机设定两个基因交叉位置,将父辈两个个体在这两个交叉点之间的基因链码相互交换,从而形成新的个体;区域交叉法是随机在染色体中选择一个交叉区域,将第二条染色体的交叉区域加在第一条染色体的前面,第一条染色体的交叉区域加在第二条染色体的前面,在交叉区域后依次删除与交叉区域相同的基因,得到最后的两条子染色体.
将第(3)步得到的关于A,B种群的数据分别用两种交叉算法来实现操作. 其中一半数据用两点交叉法,另一半的数据用区域交叉法来进行染色体的交叉重组.
其具体算法的MATLAB程序实现见附件四.
经过交叉重组得出的A、B群体数据矩阵为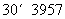 ,因数据量太大,文中就不给出具体数据.
,因数据量太大,文中就不给出具体数据.
(6)染色体的变异
为了避免过早收敛,依据选择性集成思想选择邻居交换变异和两点交换变异这两种个性好且差异性较大的变异方法,等概率使用以扩大搜索范围.
其中,邻居交换变异是产生一个随机数,将该数对应的基因和其后的基因交换;若该数对应的基因是染色体中的最后一个基因,则将该基因与染色体的第一个基因交换;两点交换变异是先产生两个不同的随机数,确定两个交换点,然后对个体在此两点的基因进行交换.
经过染色体变异得出的A、B群体数据矩阵为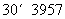 ,因数据量太大,文中就不给出具体数据.
,因数据量太大,文中就不给出具体数据.
(7)种群交叉
将两个种群中的最优解取出,再在每个种群中随机选取n个染色体,将这n+1个染色体互换,进入对方种群.
经过种群交叉得出的A、B群体数据矩阵为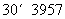 ,因数据量太大,文中就不给出具体数据.
,因数据量太大,文中就不给出具体数据.
(8)最佳个体保留法
要把群体中适应度最高的个体不经过配对交叉直接复制到下一代中,然后从
新群体中淘汰一个适应度最差的个体. 分别对A、B进行独立的操作.
经过最佳保留法选择后得出的A、B群体数据矩阵为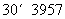 ,因数据量太大,文中就不给出具体数据.
,因数据量太大,文中就不给出具体数据.
(9)迭代的结束条件
在本文中,采用进化的代数N作为循环迭代过程的结束,如果等于N,则算法结束,输出适应值最高的解;否则,继续重复上述过程.
重复步骤(3),(4),(5),(6),(7),(8)依次进行循环迭代,本题中设定迭代次数为N=1000. 最后得到30个近似的最优解.
以上(2)—(9)流程的MATLAB程序实现见附件二.
(10)结果
选出这30个近似最优解中以时间作为权值最小的那一组解作为题设中要求的近似最优解. 其中满足要求的基因链码(站点数)的顺序即是顾客所需从起始点到终点站的路线
1.2.2 从起点站到终点站转一次车
从起点站到终点站转一次车遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
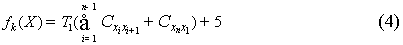
其中5(分钟)表示公汽换乘公汽一次耗时(其中步行时间2分钟).
除这之外,这一流程中的其他的原理没变.
1.2.3 从起点站到终点站转两次车
从起点站到终点站转两次车遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
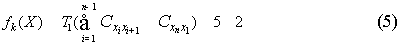
其中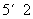 (分钟)表示公汽换乘公汽两次耗时(其中步行时间
(分钟)表示公汽换乘公汽两次耗时(其中步行时间 分钟).
分钟).
除这之外,这一流程中的其他的原理没变.
1.3 模型求解
1.3.1从起点站到终点站不转车
由程序运行最终得出:找不一条路线使从起点站到终点站不转车.
1.3.2 从起点站到终点站转一次车

1.3.3从起点站到终点站转两次车

(二)问题二
2.1 问题分析
考虑到加入地铁及公汽的交叉通道,在数据处理上用时间加权把地铁站点和汽车站点统一化,可得所有站点之间的邻接矩阵. 其求解原理与问题一相似,但由转车方式的不同就会生成相对应的适应度函数,再根据适应度函来对问题求解.
2.2 模型建立
2.2.1 产生邻接矩阵
首先运用MATLAB强大的矩阵运算功能把其邻接矩阵得出,该矩阵是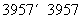 ,由于数据量太大不能把其具体表示出来,只能把所得到的数据放在内存中,在运用的时候再从内存中调用.
,由于数据量太大不能把其具体表示出来,只能把所得到的数据放在内存中,在运用的时候再从内存中调用.
2.2.2 只坐地铁(不换乘)
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
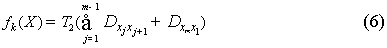
其中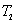 表示相邻地铁站平均行驶时间(包括停站时间),
表示相邻地铁站平均行驶时间(包括停站时间),
 表示站点
表示站点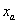 和
和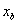 之间的距离,
之间的距离,
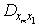 表示起始点与终点站之间的距离.
表示起始点与终点站之间的距离.
除这之外,这一流程中的其他的原理没变.
2.2.3 地铁到地铁(换乘一或两次)
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
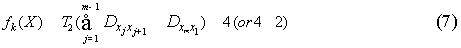
其中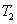 (2.5(分钟))表示相邻地铁站平均行驶时间(包括停站时间),
(2.5(分钟))表示相邻地铁站平均行驶时间(包括停站时间),
 表示站点
表示站点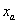 和
和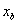 之间的距离,
之间的距离,
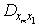 表示起始点与终点站之间的距离,
表示起始点与终点站之间的距离,
4(分钟)表示地铁换乘地铁平均耗时(其中步行时间2分钟).
除这之外,这一流程中的其他的原理没变.
2.2.4 地铁到公汽
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:

除这之外,这一流程中的其他的原理没变.
2.2.5 公汽到地铁
为了简化模型,将地铁换乘公汽平均耗时与公汽换乘地铁平均耗时都假设为7分钟,因为耗时相差不大. 则地铁到公汽与公汽到地铁是一样的.
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
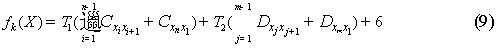
除这之外,这一流程中的其他的原理没变.
2.2.6 公汽到地铁再到公汽
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
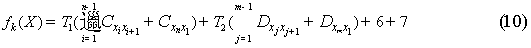
除这之外,这一流程中的其他的原理没变.
2.2.7公汽到地铁再到地铁
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:

除这之外,这一流程中的其他的原理没变.
2.2.8地铁到公汽再到公汽
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
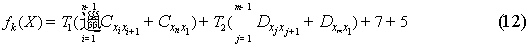 除这之外,这一流程中的其他的原理没变.
除这之外,这一流程中的其他的原理没变.
2.2.9地铁到公汽再到地铁
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
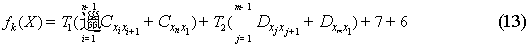 除这之外,这一流程中的其他的原理没变.
除这之外,这一流程中的其他的原理没变.
2.3 模型求解
2.3.1 只坐地铁
由程序运行最终得出:对六对起点到终点找不一条路线为只做地铁.
2.3.2 地铁到地铁
由程序运行最终得出:对六对起点到终点找不一条路线地铁到地铁.
2.3.3 地铁到公汽
由程序运行最终得出:对六对起点到终点找不一条路线为地铁到公汽.
2.3.4 公汽到地铁
由程序运行最终得出:对六对起点到终点找不一条路线为公汽到地铁.
2.3.5 公汽到公汽
1.换一次车
2.换两次车

2.3.6 公汽到地铁再到地铁
由程序运行最终得出:对六对起点到终点找不一条路线为公汽到地铁再到地铁.
2.3.7 地铁到公汽再到公汽
由程序运行最终得出:对六对起点到终点找不一条路线为地铁到公汽再到公汽.
2.3.8 地铁到公汽再到地铁
由程序运行最终得出:对六对起点到终点找不一条路线为地铁到公汽再到地铁.
(三)问题三
3.1 问题分析
在该问题中假设知道所有站点之间的步行时间,即任意两个站点之间都是可以到达的,只是以步行的方式来实现. 我们以两个站点之间的步行时间作为矩阵中的权. 这时构建的邻接矩阵中的权由两站点之间公汽到公汽的时间,公汽到地铁的时间,地铁到公汽的时间,地铁到地铁的时间和两点之间的步行时间构成.
3.2 模型建立
对于该问题遗传算法流程中基于站点序号的编码,交叉重组,染色体的变异,种群交叉,迭代的结束条件和结果的原理与仅考虑公汽线路从起点站到终点站不转车相同.
只有在适应度函数与选择流程中每一个个体所对应的适应度函数处有所改变,其函数为:
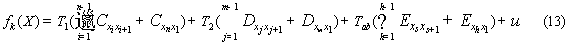 其中
其中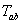 表示任意两个站点之间的步行时间,
表示任意两个站点之间的步行时间,
 表示站点
表示站点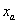 和
和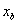 之间的距离,
之间的距离,
 表示起始点与终点站之间的距离,
表示起始点与终点站之间的距离,
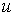 表示转车换乘所耗时间总和.
表示转车换乘所耗时间总和.
除这之外,这一流程中的其他的原理没变.
五、模型的误差分析
本文针对公交线路问题釆用的是双种群遗传算法,其中运用到的思想为基于双种群初始群体,对染色体进行整数编码,再通过竞争选择法对其染色体进行选择,依据选择性集成思想,等概率使用遗传算子分别对染色体的交叉与变异进行操作,在这之中每一个算法思想均是想尽力扩大其搜索范围,减缓其收敛度. 其中交叉率与变异率不同,就会造成结果与最优解存在不同产差异.
六、模型的评价
1.模型的优点
1.1 遗传算法与其他搜索算法相比较:遗传变异法不是直接作用在参变量群上,而是作用在这个群的某种编码上;遗传算法从初始解群体开始搜索,不是从单个解开始搜索,算法具有较高的并行性;遗传算法在搜索过程中只使用适应度函数计算,而不用导数或其他信息,具有较强的通用性;遗传算法使用概率转换规则而不是使用确定性的规则,具有全局寻优的特点.
1.2 本文设计了针对公汽线路系统特点的整数编码的遗传算法,基于两个初始种群,运用竞争选择法来对染色体进行选择并保留若干最佳个体,并使用相应的等概率交叉算子和等概率变异算子实现算法,取得了良好的效果.
1.3本文所釆用的双种群遗传算法是一种并行遗传算法,它使用两个种群同时进化,并交换种群之间优秀个体所携带的遗传信息增加个体的多样性,扩展解的搜索空间,以打破种群内的平衡态达到更高的平衡态,跳出局部最优. 收敛时最优结果,所花时间和迭代次数等方面单双种群遗传算法都优于一般遗传算法.
1.4 在进行染色体的选择时,我们采用了一种新的赌轮选择算子——离散赌轮选择算子,将有效地避免了整个群体多样性无法得到保证问题.
1.5 忽略复杂计算. 例如可以对交叉操作后的修正操作适度简化甚至可以全部去掉,只需要作出保证遗传可正常进行的操作即可.
2.模型的不足
本文所釆用的算法所花费的运算时间相对其他的搜索算法较长.
七、模型的改进及推广
1.模型的改进
1.1 在进行染色体变异操作中,在运用等概率变异算子时,可再加入其他的个性好且差异性较大的变异方法,使用以扩大搜索范围.
1.2 在算法实施过程中,初始群体大小,迭代次数,交叉概率,变异概率等参数值的设定对于问题能否找到满意解起着非常重要的作用.如果初始群体大小与迭代次数太小,则不容易找到最优解,反之,则计算时间长. 对于交叉概率来说,如果取值过大,则会破坏以前遗传的结果,因而交叉概率不能取得太大. 对于变异概率,其目的是为了保证算法对解空间的覆盖,但其太大,会破坏遗传和交叉选出的染色体而变成随机搜索,反之,染色体种群又会过于单调,从而陷入局部极值. 因此在实际计算时,要根据具体问题,来选择合适的参数.
2.模型的推广
解决公汽线路问题的算法在对钻孔路线方案,物流配送系统,网络布线,铁路网优化等问题中有着广泛的应用,所以改进和研究解决公汽线路问题的算法对实际的工业生产是有重要意义的.
八、参考文献
[1] 张立科,MATLAB 7.0从入门到精通[M],北京:人民邮电出版社,2006.
[2] 赵静,但琦,数学建模与数学实验(第2版)[M],北京:高等教育出版社,2003.
[3] 汪国强,数学建模优秀案例选编[M],广州:华南理工大出版社,2001.
[4] 阎平凡,张长水,人工神经网络与模拟进化计算(第2版)[M],北京:清华大学出版社,2005,(549-609).
[5] 李飞,白艳萍,用遗传算法求解旅行商问题[J],中北大学学报(自然科学版),28(1):49-52,2007.
[6] 赵燕伟,吴斌,蒋丽,董红召,王万良,车辆路径问题的双种群遗传算法求解法[J],计算机集成制造系统-CIMS, 10(30):303-306,2004.
[7] 蒋望东,林士敏,基于选择性集成的整数编码遗传算法及TSP问题求解[J],计算机与现代化,(5):38-40,2007.
[8] 吴值民,吴凤丽,邹赟波,李宏伟,卢厚清,退火单亲求解旅行商问题及MAYLAB实现[J],解放军理工大学学报(自然科学版),8(1):44-48,2007.
[9] 周涛,基于改进遗传算法的TSP问题研究[J],微电子学与计算机, 23(10):104-106,2006.
九、附录
附件一
%产生邻接矩阵
clear;
clc;
load bssj;
i3=zeros(3958,3958);
for i1=1:520
for i2=2:87
for i4=2:90
a1=data((find(data(:,1)==i1)+2),i4);
a2=data(find(data(:,1)==i1)+2,i2);
if a1~=0 & (i4-i2)==0 %a1不为空值时,把i3矩阵赋值
i3(a2,a1)=0;
elseif a1~=0 & (i4-i2)==1
i3(a2,a1)=3;
elseif a1~=0 & (i4-i2)>1
i3(a2,a1)=inf;
elseif a1==0
break
end
a3=data((find(data(:,1)==i1)+3),i4);
a4=data(find(data(:,1)==i1)+3,i2);
if a3~=0 & (i4-i2)==0 %a1不为空值时,把i3矩阵赋值
i3(a3,a4)=0;
elseif a3~=0 & (i4-i2)==1
i3(a3,a4)=3;
elseif a3~=0 & (i4-i2)>1
i3(a3,a4)=inf;
elseif a3==0
break
end
end
end
end
for j1=1:3958
for j2=1:3958
if j1~=j2 & i3(j1,j2)~=3
i3(j1,j2)=inf;
elseif j1==j2
i3(j1,j2)=0;
end
end
end
附件二
%遗传算法流程实现
%yic.m
clear;
clc;
M=30;
num=3957;
popm1=zeros(M,num); %生成初始群体1
for k1=1:M
popm1(k1,:)=randperm(num); %随机产生一个由自然数1到num 组成的全排列
end
popm2=zeros(M,num); %生成初始群体2
for k2=1:M
popm2(k2,:)=randperm(num); %随机产生一个由自然数1到num 组成的全排列
end
a1=3395;
a2=1828;
a3=[];
a4=[];
for k3=1:30
a3(k3)=abs(find(popm1(k3,:)==a1)-find(popm1(k3,:)==a2));%群体1中,不同个体a1和a2的站点差
a4(k3)=abs(find(popm2(k3,:)==a1)-find(popm2(k3,:)==a2));%群体2中,不同个体a1和a2的站点差
end
a5=3.*a3+3956*3;%种群1的不同个体适应度
a6=3.*a4+3956*3;%种群1的不同个体适应度
a7=[];
a8=[];
a7=(a5./sum(a5)).*1000;%种群1的不同个体选择概率
a8=(a6./sum(a6)).*1000;%种群2的不同个体选择概率
a11=0;
a12=[];
for k4=1:30
a11=a11+a7(k4);%种群1累加区间
a12(k4)=a11;
end
a13=0;
a14=[];
for k5=1:30
a13=a13+a8(k5);%种群2累加区间
a14(k5)=a13;
end
a15=unifrnd(1,1000,1,30);%种群1产生30个1-1000的均匀分布的随机数
a16=unifrnd(1,1000,1,30);%种群2产生30个1-1000的均匀分布的随机数
a17=[];%种群1
for k6=1:30
if a15(k6)<=a12(1)
a17(k6)=1;
elseif a12(1)<(a15(k6)) &(a15(k6))<=a12(2)
a17(k6)=2;
elseif a12(2)<(a15(k6)) & (a15(k6))<=a12(3)
a17(k6)=3;
elseif a12(3)<(a15(k6)) & (a15(k6))<=a12(4)
a17(k6)=4;
elseif a12(4)<(a15(k6)) & (a15(k6))<=a12(5)
a17(k6)=5;
elseif a12(5)<(a15(k6)) & (a15(k6))<=a12(6)
a17(k6)=6;
elseif a12(6)<(a15(k6)) & (a15(k6))<=a12(7)
a17(k6)=7;
elseif a12(7)<(a15(k6)) & (a15(k6))<=a12(8)
a17(k6)=8;
elseif a12(8)<(a15(k6)) & (a15(k6))<=a12(9)
a17(k6)=9;
elseif a12(9)<(a15(k6)) & (a15(k6))<=a12(10)
a17(k6)=10;
elseif a12(10)<(a15(k6)) & (a15(k6))<=a12(11)
a17(k6)=11;
elseif a12(11)<(a15(k6)) & (a15(k6))<=a12(12)
a17(k6)=12;
elseif a12(12)<(a15(k6)) & (a15(k6))<=a12(13)
a17(k6)=13;
elseif a12(13)<(a15(k6)) & (a15(k6))<=a12(14)
a17(k6)=14;
elseif a12(14)<(a15(k6)) & (a15(k6))<=a12(15)
a17(k6)=15;
elseif a12(15)<(a15(k6)) & (a15(k6))<=a12(16)
a17(k6)=16;
elseif a12(16)<(a15(k6)) & (a15(k6))<=a12(17)
a17(k6)=17;
elseif a12(17)<(a15(k6)) & (a15(k6))<=a12(18)
a17(k6)=18;
elseif a12(18)<(a15(k6)) & (a15(k6))<=a12(19)
a17(k6)=19;
elseif a12(19)<(a15(k6)) & (a15(k6))<=a12(20)
a17(k6)=20;
elseif a12(20)<(a15(k6)) & (a15(k6))<=a12(21)
a17(k6)=21;
elseif a12(21)<(a15(k6)) & (a15(k6))<=a12(22)
a17(k6)=22;
elseif a12(22)<(a15(k6)) & (a15(k6))<=a12(23)
a17(k6)=23;
elseif a12(23)<(a15(k6)) & (a15(k6))<=a12(24)
a17(k6)=24;
elseif a12(24)<(a15(k6)) & (a15(k6))<=a12(25)
a17(k6)=25;
elseif a12(25)<(a15(k6)) & (a15(k6))<=a12(26)
a17(k6)=26;
elseif a12(26)<(a15(k6)) & (a15(k6))<=a12(27)
a17(k6)=27;
elseif a12(27)<(a15(k6)) & (a15(k6))<=a12(28)
a17(k6)=28;
elseif a12(28)<(a15(k6)) & (a15(k6))<=a12(29)
a17(k6)=29;
elseif a12(29)<(a15(k6)) & (a15(k6))<=a12(30)
a17(k6)=30;
end
end
a18=[];%种群2
for k7=1:30
if a16(k7)<=a14(1)
a18(k7)=1;
elseif a14(1)<(a16(k7)) &(a16(k7))<=a14(2)
a18(k7)=2;
elseif a14(2)<(a16(k7)) & (a16(k7))<=a14(3)
a18(k7)=3;
elseif a14(3)<(a16(k7)) & (a16(k7))<=a14(4)
a18(k7)=4;
elseif a14(4)<(a16(k7)) & (a16(k7))<=a14(5)
a18(k7)=5;
elseif a14(5)<(a16(k7)) & (a16(k7))<=a14(6)
a18(k7)=6;
elseif a14(6)<(a16(k7)) & (a16(k7))<=a14(7)
a18(k7)=7;
elseif a14(7)<(a16(k7)) & (a16(k7))<=a14(8)
a18(k7)=8;
elseif a14(8)<(a16(k7)) & (a16(k7))<=a14(9)
a18(k7)=9;
elseif a14(9)<(a16(k7)) & (a16(k7))<=a14(10)
a18(k7)=10;
elseif a14(10)<(a16(k7)) & (a16(k7))<=a14(11)
a18(k7)=11;
elseif a14(11)<(a16(k7)) & (a16(k7))<=a14(12)
a18(k7)=12;
elseif a14(12)<(a16(k7)) & (a16(k7))<=a14(13)
a18(k7)=13;
elseif a14(13)<(a16(k7)) & (a16(k7))<=a14(14)
a18(k7)=14;
elseif a14(14)<(a16(k7)) & (a16(k7))<=a14(15)
a18(k7)=15;
elseif a14(15)<(a16(k7)) & (a16(k7))<=a14(16)
a18(k7)=16;
elseif a14(16)<(a16(k7)) & (a16(k7))<=a14(17)
a18(k7)=17;
elseif a14(17)<(a16(k7)) & (a16(k7))<=a14(18)
a18(k7)=18;
elseif a14(18)<(a16(k7)) & (a16(k7))<=a14(19)
a18(k7)=19;
elseif a14(19)<(a16(k7)) & (a16(k7))<=a14(20)
a18(k7)=20;
elseif a14(20)<(a16(k7)) & (a16(k7))<=a14(21)
a18(k7)=21;
elseif a14(21)<(a16(k7)) & (a16(k7))<=a14(22)
a18(k7)=22;
elseif a14(22)<(a16(k7)) & (a16(k7))<=a14(23)
a18(k7)=23;
elseif a14(23)<(a16(k7)) & (a16(k7))<=a14(24)
a18(k7)=24;
elseif a14(24)<(a16(k7)) & (a16(k7))<=a14(25)
a18(k7)=25;
elseif a14(25)<(a16(k7)) & (a16(k7))<=a14(26)
a18(k7)=26;
elseif a14(26)<(a16(k7)) & (a16(k7))<=a14(27)
a18(k7)=27;
elseif a14(27)<(a16(k7)) & (a16(k7))<=a14(28)
a18(k7)=28;
elseif a14(28)<(a16(k7)) & (a16(k7))<=a14(29)
a18(k7)=29;
elseif a14(29)<(a16(k7)) & (a16(k7))<=a14(30)
a18(k7)=30;
end
end
a19=[,];
a20=[,];
for k9=1:30
a19(k9,:)=popm1(a17(k9),:);
a20(k9,:)=popm2(a18(k9),:);
end
a22=[,];a23=[,];
for r1=1:2:30
a=a19(r1,:);
b=a19(r1+1,:);
p1=min(fix(unifrnd(1,3957,1,2)));
p2=max(fix(unifrnd(1,3957,1,2)));
a1=[b(p1:p2),a];
b1=[a(p1:p2),b];
for j=p2-p1+2:3957+p2-p1+1
for i=1:p2-p1+1
if(a1(j)==a1(i))
a1(j)=nan;
end
if(b1(j)==b1(i))
b1(j)=nan;
end
end
end
if r1==1
a22(r1,:)=a1(~isnan(a1));
a22(r1+1,:)=b1(~isnan(b1));
elseif r1~=1
a23(r1-2,:)=a1(~isnan(a1));
a23(r1-1,:)=b1(~isnan(b1));
end
end
a2=[a22;a23];
b22=[,];,b23=[,];
for r2=1:2:30
a=a20(r2,:);
b=a20(r2+1,:);
p1=min(fix(unifrnd(1,3957,1,2)));
p2=max(fix(unifrnd(1,3957,1,2)));
a1=[b(p1:p2),a];
b1=[a(p1:p2),b];
for j=p2-p1+2:3957+p2-p1+1
for i=1:p2-p1+1
if(a1(j)==a1(i))
a1(j)=nan;
end
if(b1(j)==b1(i))
b1(j)=nan;
end
end
end
if r2==1
b22(r2,:)=a1(~isnan(a1));
b22(r2+1,:)=b1(~isnan(b1));
elseif r2~=1
b23(r2-2,:)=a1(~isnan(a1));
b23(r2-1,:)=b1(~isnan(b1));
end
end
b2=[b22;b23];
w1=[,];
w2=[,];
for q=1:15
z1=fix(unifrnd(1,3957,1,1));
z2=fix(unifrnd(1,3957,1,1));
z3=a2(q,z1);z5=a2(q,z1+1);
z4=b2(q,z2);z6=a2(q,z1+1);
w1(q,:)=[a2(q,1:z1-1),z5,z3,a2(q,(z1+2):3957)];
w2(q,:)=[b2(q,1:z1-1),z6,z4,b2(q,(z1+2):3957)];
end
w3=[,];
w4=[,];
for q=16:30
z1=fix(unifrnd(1,3957,1,2));
z2=fix(unifrnd(1,3957,1,2));
z11=max(z1);
z12=min(z1);
z21=max(z2);
z22=min(z2);
z3=a2(q,z12);z5=a2(q,z11);
z4=b2(q,z22);z6=a2(q,z21);
w3(q-15,:)=[a2(q,1:z12-1),z5,a2(q,z12+1:z11-1),z3,a2(q,(z11+1):3957)];
w4(q-15,:)=[b2(q,1:z22-1),z6,b2(q,z22+1:z21-1),z4,b2(q,(z21+1):3957)];
end
w5=[w1;w3];
w6=[w2;w4];
%jiaoc.m
a22=[,];a23=[,];
for r1=1:2:30
a=a19(r1,:);
b=a19(r1+1,:);
p1=min(fix(unifrnd(1,3957,1,2)));
p2=max(fix(unifrnd(1,3957,1,2)));
a1=[b(p1:p2),a];
b1=[a(p1:p2),b];
for j=p2-p1+2:3957+p2-p1+1
for i=1:p2-p1+1
if(a1(j)==a1(i))
a1(j)=nan;
end
if(b1(j)==b1(i))
b1(j)=nan;
end
end
end
if r1==1
a22(r1,:)=a1(~isnan(a1));
a22(r1+1,:)=b1(~isnan(b1));
elseif r1~=1
a23(r1-2,:)=a1(~isnan(a1));
a23(r1-1,:)=b1(~isnan(b1));
end
end
a2=[a22;a23];
b22=[,];,b23=[,];
for r2=1:2:30
a=a20(r2,:);
b=a20(r2+1,:);
p1=min(fix(unifrnd(1,3957,1,2)));
p2=max(fix(unifrnd(1,3957,1,2)));
a1=[b(p1:p2),a];
b1=[a(p1:p2),b];
for j=p2-p1+2:3957+p2-p1+1
for i=1:p2-p1+1
if(a1(j)==a1(i))
a1(j)=nan;
end
if(b1(j)==b1(i))
b1(j)=nan;
end
end
end
if r2==1
b22(r2,:)=a1(~isnan(a1));
b22(r2+1,:)=b1(~isnan(b1));
elseif r2~=1
b23(r2-2,:)=a1(~isnan(a1));
b23(r2-1,:)=b1(~isnan(b1));
end
end
b2=[b22;b23];
%biany.m
w1=[,];
w2=[,];
for q=1:15
z1=fix(unifrnd(1,3957,1,1));
z2=fix(unifrnd(1,3957,1,1));
z3=a2(q,z1);z5=a2(q,z1+1);
z4=b2(q,z2);z6=a2(q,z1+1);
w1(q,:)=[a2(q,1:z1-1),z5,z3,a2(q,(z1+2):3957)];
w2(q,:)=[b2(q,1:z1-1),z6,z4,b2(q,(z1+2):3957)];
end
w3=[,];
w4=[,];
for q=16:30
z1=fix(unifrnd(1,3957,1,2));
z2=fix(unifrnd(1,3957,1,2));
z11=max(z1);
z12=min(z1);
z21=max(z2);
z22=min(z2);
z3=a2(q,z12);z5=a2(q,z11);
z4=b2(q,z22);z6=a2(q,z21);
w3(q-15,:)=[a2(q,1:z12-1),z5,a2(q,z12+1:z11-1),z3,a2(q,(z11+1):3957)];
w4(q-15,:)=[b2(q,1:z22-1),z6,b2(q,z22+1:z21-1),z4,b2(q,(z21+1):3957)];
end
w5=[w1;w3];
w6=[w2;w4];
