逆矩阵的几种求法与解析
矩阵是线性代数的主要内容,很多实际问题用矩阵的思想去解既简单又快捷.逆矩阵又是矩阵理论的很重要的内容, 逆矩阵的求法自然也就成为线性代数研究的主要内容之一.本文将给出几种求逆矩阵的方法.
1.利用定义求逆矩阵
定义: 设A、B 都是n 阶方阵, 如果存在n 阶方阵B 使得AB= BA = E, 则称A为可逆矩阵, 而称B为A 的逆矩阵.下面举例说明这种方法的应用.
例1 求证: 如果方阵A 满足A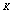 = 0, 那么E-A是可逆矩阵, 且
= 0, 那么E-A是可逆矩阵, 且
(E-A) = E + A + A
= E + A + A +…+A
+…+A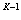
证明 因为E 与A 可以交换, 所以
(E- A )(E+A + A +…+ A
+…+ A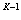 )= E-A
)= E-A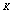 ,
,
因A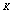 = 0 ,于是得
= 0 ,于是得
(E-A)(E+A+A +…+A
+…+A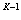 )=E,
)=E,
同理可得(E + A + A +…+A
+…+A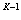 )(E-A)=E,
)(E-A)=E,
因此E-A是可逆矩阵,且
(E-A) = E + A + A
= E + A + A +…+A
+…+A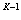 .
.
同理可以证明(E+ A)也可逆,且
(E+ A) = E -A + A
= E -A + A +…+(-1)
+…+(-1)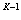 A
A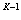 .
.
由此可知, 只要满足A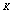 =0,就可以利用此题求出一类矩阵E
=0,就可以利用此题求出一类矩阵E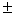 A的逆矩阵.
A的逆矩阵.
例2 设 A =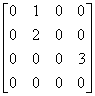 ,求 E-A的逆矩阵.
,求 E-A的逆矩阵.
分析 由于A中有许多元素为零, 考虑A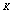 是否为零矩阵, 若为零矩阵, 则可以采用例2 的方法求E-A的逆矩阵.
是否为零矩阵, 若为零矩阵, 则可以采用例2 的方法求E-A的逆矩阵.
解 容易验证
A =
=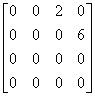 , A
, A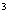 =
=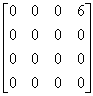 , A
, A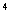 =0
=0
而 (E-A)(E+A+ A + A
+ A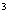 )=E,所以
)=E,所以
(E-A) = E+A+ A
= E+A+ A + A
+ A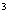 =
=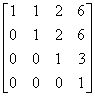 .
.
2.初等变换法
求元素为具体数字的矩阵的逆矩阵,常用初等变换法.如果A可逆,则A可通过初等变换,化为单位矩阵I,即存在初等矩阵 使
使
(1)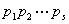 A=I,用A
A=I,用A 右乘上式两端,得:
右乘上式两端,得:
(2) 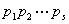 I= A
I= A
比较(1)(2)两式,可以看到当A通过初等变换化为单位矩阵的同时,对单位矩阵I作同样的初等变换,就化为A的逆矩阵A .
.
用矩阵表示(A I)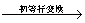 为(I A
为(I A ),就是求逆矩阵的初等行变换法,它是实际应用中比较简单的一种方法.需要注意的是,在作初等变换时只允许作行初等变换.同样,只用列初等变换也可以求逆矩阵.
),就是求逆矩阵的初等行变换法,它是实际应用中比较简单的一种方法.需要注意的是,在作初等变换时只允许作行初等变换.同样,只用列初等变换也可以求逆矩阵.
例1 求矩阵A的逆矩阵.已知A=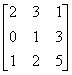 .
.
解 [A I]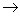

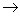

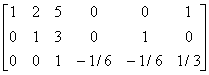
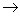
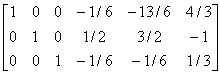
故 A =
= .
.
在事先不知道n阶矩阵是否可逆的情况下,也可以直接用此方法.如果在初等变换过程中发现左边的矩阵有一行元素全为0,则意味着A不可逆,因为此时表明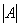 =0,则A
=0,则A 不存在.
不存在.
例2 求A=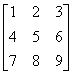 .
.
解 [A E]=
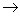
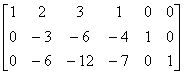
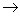
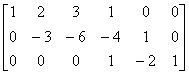 .
.
由于左端矩阵中有一行元素全为0,于是它不可逆,因此A不可逆.
3.伴随阵法
定理 n阶矩阵A=[a ]为可逆的充分必要条件是A非奇异.且
]为可逆的充分必要条件是A非奇异.且
A =
=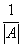

其中A 是
是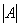 中元素a
中元素a 的代数余子式.
的代数余子式.
矩阵 称为矩阵A的伴随矩阵,记作A*,于是有A
称为矩阵A的伴随矩阵,记作A*,于是有A =
=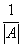 A*.
A*.
证明 必要性:设A可逆,由A A =I,有
=I,有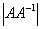 =
=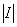 ,则
,则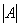
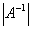 =
=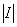 ,所以
,所以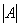
 0,即A为非奇异.
0,即A为非奇异.
充分性: 设A为非奇异,存在矩阵
B=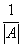
 ,
,
其中
AB=
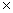
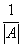

=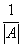
 =
= =I
=I
同理可证BA=I.
由此可知,若A可逆,则A =
=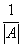 A*.
A*.
用此方法求逆矩阵,对于小型矩阵,特别是二阶方阵求逆既方便、快阵,又有规律可循.因为二阶可逆矩阵的伴随矩阵,只需要将主对角线元素的位置互换,次对角线的元素变号即可.
若可逆矩阵是三阶或三阶以上矩阵,在求逆矩阵的过程中,需要求9个或9个以上代数余子式,还要计算一个三阶或三阶以上行列式,工作量大且中途难免
出现符号及计算的差错.对于求出的逆矩阵是否正确,一般要通过AA =I来检验.一旦发现错误,必须对每一计算逐一排查.
=I来检验.一旦发现错误,必须对每一计算逐一排查.
4.分块矩阵求逆法
4.1.准对角形矩阵的求逆
命题 设A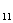 、A
、A 都是非奇异矩阵,且A
都是非奇异矩阵,且A 为n阶方阵,A
为n阶方阵,A 为m阶方阵
为m阶方阵

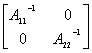
证明 因为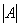 =
= =
=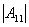

 0, 所以A可逆.
0, 所以A可逆.
设A =
=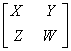 ,于是有
,于是有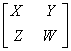
 =
=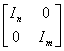 ,
,
其中 X A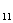 =I
=I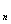 , Y A
, Y A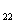 =0,Z A
=0,Z A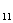 =0,W A
=0,W A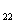 =I
=I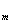 .又因为A
.又因为A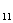 、A
、A 都可逆,用A
都可逆,用A 、A
、A 分别右乘上面左右两组等式得:
分别右乘上面左右两组等式得:
X= A ,Y=0,Z=0,W= A
,Y=0,Z=0,W= A
故 A =
= 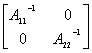
把上述结论推广到每一个子块都是非奇异矩阵的准对角形状矩阵中去,即:
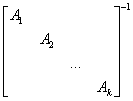 =
=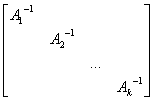
4.2.准三角形矩阵求逆
命题 设A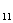 、A
、A 都是非奇异矩阵,则有
都是非奇异矩阵,则有
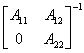 =
=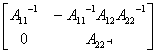
证明 因为
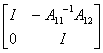 =
=
两边求逆得
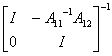
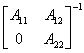 =
=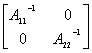
所以 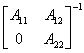 =
=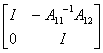
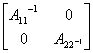
=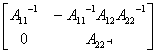
同理可证
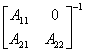 =
=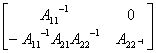
此方法适用于大型且能化成对角子块阵或三角块阵的矩阵. 是特殊方阵求逆的一种方法,并且在求逆矩阵之前,首先要将已给定矩阵进行合理分块后方能使用.
5.恒等变形法
恒等变形法求逆矩阵的理论依据为逆矩阵的定义,此方法也常用与矩阵的理论推导上.就是通过恒等变形把要求的值化简出来,题目中的逆矩阵可以不求,利用AA =E,把题目中的逆矩阵化简掉。
=E,把题目中的逆矩阵化简掉。
例1 计算(A+4E)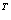 (4E-A)
(4E-A) (16E-A
(16E-A )的行列式,其中 A=
)的行列式,其中 A=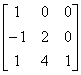
解 令 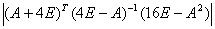 =D
=D
D=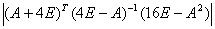
=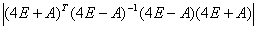
=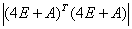 =
=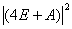 .
.
虽然题目中出现了(4E-A) .但是经过化简之后不再出现此式,因此得
.但是经过化简之后不再出现此式,因此得
D=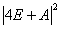 =22500.
=22500.
例2 已知 n阶矩阵A满足A +2A-3E=0.求证:A+4E可逆并求出A+4E的逆.
+2A-3E=0.求证:A+4E可逆并求出A+4E的逆.
证明 把A +2A-3E=0变形为A
+2A-3E=0变形为A +2A-8E=-5E,即
+2A-8E=-5E,即
(A+4E)(A-2E)=-5E,可得(A+4E)(-A/5+2E/5)=E,
所以存在一个矩阵B=-A/5+2E/5,使(A+4E)B=E,由定义得A+4E可逆,且
(A+4E)
 =B=-A/5+2E/5.
=B=-A/5+2E/5.
另外,有些计算命题中虽出现逆矩阵,但通过适当的矩阵运算可消去,因而不必急于求出逆矩阵.
6.利用线性方程组求逆矩阵
6.1若n阶矩阵A可逆,则A A =E,于是A
=E,于是A 的第j列Xj是线性方程组AXj=Ej的解,j=1,2,…,n, Ej是第j个分量是1的单位向量.因此,我们可以去解线性方程组AX=B,
的第j列Xj是线性方程组AXj=Ej的解,j=1,2,…,n, Ej是第j个分量是1的单位向量.因此,我们可以去解线性方程组AX=B,
其中B=(b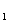 ,b
,b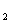 ,…,b
,…,b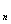 )
)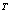 , 然后在所求的解中把B=(b
, 然后在所求的解中把B=(b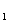 ,b
,b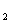 ,…,b
,…,b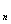 )
)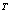 列,分别用
列,分别用
E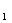 =(1,0,0,…,0)
=(1,0,0,…,0)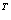 ,
,
E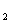 =(0,1,0,…,0)
=(0,1,0,…,0)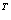 ,
,
……,
E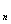 =(0,0,0,…,1)
=(0,0,0,…,1)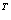
代替,便可以求得A 的第1,2,…n列,所以A-1= (X
的第1,2,…n列,所以A-1= (X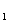 ,X
,X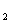 ,…,X
,…,X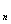 ).这种方法在某些时候可能比初等变换法求逆矩阵稍微简一点.下面例子说明该方法的应用.
).这种方法在某些时候可能比初等变换法求逆矩阵稍微简一点.下面例子说明该方法的应用.
6.2若n阶矩阵A可逆,则A A =E
=E
令A-1= X=(x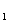 ,x
,x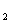 ,…,x
,…,x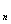 )
)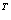 E=B=(b
E=B=(b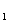 ,b
,b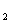 ,…,b
,…,b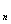 )
)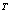 (x,b皆为行向量)
(x,b皆为行向量)
则A A =E变为AX=B
=E变为AX=B
因此,我们可以去解线性方程组AX=B, 然后把所求的解的公式中的b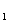 ,b
,b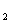 ,…,b
,…,b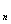 分别用
分别用
b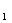 =(1,0,0,…,0),
=(1,0,0,…,0),
b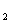 =(0,1,0,…,0),
=(0,1,0,…,0),
……,
b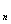 =(0,0,0,…,1)
=(0,0,0,…,1)
代替,便可以求得x ,x
,x ,x
,x ,x
,x ,x
,x ,所以A-1= X=(x
,所以A-1= X=(x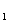 ,x
,x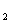 ,…,x
,…,x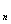 )
)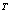
例 求矩阵A=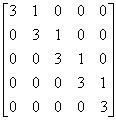 的逆矩阵.
的逆矩阵.
解 设X=(x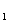 ,x
,x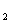 ,x
,x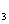 ,x
,x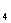 ,x
,x )
)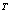 ,B=(b
,B=(b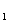 ,b
,b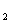 ,b
,b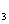 ,b
,b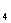 ,b
,b )
)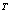 解方程组 AX=B,即:
解方程组 AX=B,即:
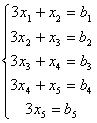
解得: 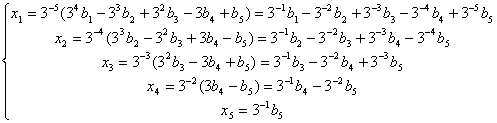
然后把B=(b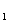 ,b
,b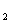 ,…,b
,…,b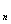 )
) 列,分别用
列,分别用
E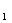 =(1,0,0,…,0)
=(1,0,0,…,0) ,
,
E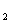 =(0,1,0,…,0)
=(0,1,0,…,0)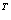 ,
,
……,
E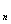 =(0,0,0,…,1)
=(0,0,0,…,1)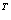
代入,得到矩阵A 的第1,2 ,3,4,5列,分别为
的第1,2 ,3,4,5列,分别为
X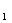 =(
=( ,0,0,0,0)
,0,0,0,0)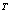 ,
,
X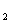 =(-3
=(-3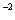 ,
, ,0,0,0)
,0,0,0)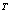 ,
,
X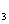 =(3
=(3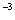 ,-3
,-3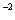 ,
, ,0,0)
,0,0)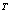 ,
,
X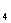 =(-3
=(-3 ,3
,3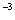 ,-3
,-3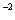 ,
, ,0)
,0)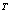 ,
,
X =(3
=(3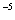 ,-3
,-3 ,3
,3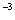 ,-3
,-3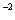 ,
, )
)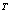
A =
=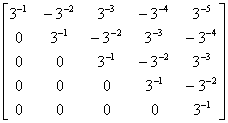 .
.
这种方法特别适用于线性方程组AX=B比较容易求解的情形,也是很多工程类问题的解决方法.
以上各种求逆方法只是我的一些粗浅的认识,也许有很多的不当之处,我希望我的这篇文章能给大家带来帮助,能帮助我们更快更准地解决好繁琐的求逆矩阵问题.同时,它还是我们更好的学习线性代数的必备基础知识,认真掌握它,可供我们以后继续在数学方面深造打下坚实的基础.但我很希望各位老师和同学给于指导.能使我的这篇文章更加完善和实用.
参 考 文 献
[1] 北京大学数学系几何与代数教研室代数小组. 高等代数[M ]. 北京: 高等教育出版社, 2001.
[2] 杨明顺. 三角矩阵求逆的一种方法[J ]. 渭南师范学院学报, 2003.
[3] 丘维声. 高等代数[M ]. 北京: 高等教育出版社,2001.
[4] 杨子胥. 高等代数习题集[M] . 济南:山东科学技术出版社,1984.
[5] 赵树原. 线性代数[M] . 北京:中国人民大学出版社,1997.
[6] 李宗铎. 求逆矩阵的一个方法[ J ] . 数学通报,1983.
[7] 贺福利等. 关于矩阵对角化的几个条件[J ] . 高等函授学报(自然科学版) ,2004 , (1)
[8] 张禾瑞.郝炳新.高等代数[M]. 北京: 高等教育出版社.1999.
[9] 王永葆. 线性代数[M].长春:东北大学出版社.2001.
[10] 同济大学遍.线性代数(第二版). 北京: 高等教育出版社,1982.
[11] 王萼芳,丘维声编,高等代数讲义. 北京大学出版社,1983.
[13] 华东师范大学数学系编.数学分析.人民教育出版社,1980
[14] 杜汉玲 求逆矩阵的方法与解析 高等函授学报(自然科学版) 第17卷第4期20##年8月
[15] 苏 敏 逆矩阵求法的进一步研究河南纺织高等专科学校学报,2004 年第16 卷第2 期
第二篇:矩阵及逆矩阵的求法
矩阵的可逆性与逆矩阵的求法
目录
摘要……………………………………………………………………………………1
第1章.矩阵…………………………………………………………………………..2
1.1矩阵的定义……………………………………………………………………2
1.2矩阵的运算……………………………………………………………………2
第2章.矩阵的可逆性及逆矩阵……………………………………………………..5
2.1矩阵的基本概念……………………………………………………………….5
2.2矩阵可逆的判断方法………………………………………………………….6
2.3矩阵可逆性的求法…………………………………………………………...10
第3章.逆矩阵的拓展.……………………………………………………………..17
3.1广义逆矩阵的引入.…………………………………………………….……17
3.2广义逆矩阵的定义及存在……………………………………………...……17
第4章.总结………………………………………………………………………….21
参考文献 ……………………………………………………………………………22
致谢 …………………………………………………………………………………23
附件:论文英文简介
矩阵的可逆性与逆矩阵的求法
[摘要]:矩阵理论是现代代数学的重要分支理论之一,它也为现代科技及现代经济理论研究提供不可或缺的数学支持。在线性代数研究中引入矩阵的目的之一就是为了研究线性方程组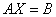 求解及更一般的矩阵方程求解提供数学工具,其中矩阵的可逆性及逆矩阵的求法是最主要的内容。本文从矩阵的基本概念及运算入手,主要探讨和归纳矩阵可逆性的四种判定方法和求逆矩阵的五种方法,并引进
求解及更一般的矩阵方程求解提供数学工具,其中矩阵的可逆性及逆矩阵的求法是最主要的内容。本文从矩阵的基本概念及运算入手,主要探讨和归纳矩阵可逆性的四种判定方法和求逆矩阵的五种方法,并引进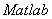 这一数学软件求逆矩阵的程序,同时关注广义逆矩阵意义及求法。
这一数学软件求逆矩阵的程序,同时关注广义逆矩阵意义及求法。
[关键词]:矩阵 可逆性 逆矩阵 广义逆 求法
矩阵可逆性的判断和可逆矩阵的求法是矩阵理论学习的重点与难点,也是研究矩阵性质及运算中必不可少的一部分。本文在分析和归纳判断矩阵的可逆性和逆矩阵的求法,给出了四种判断矩阵可逆的方法,其中有初等矩阵的应用,有行列式的应用,还有向量的线性无关和线性方程组的应用。逆矩阵的求法给出了五种方法:分别是行变换、列变换、伴随矩阵、分块矩阵法以及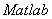 软件的解法,同时也讨论了广义逆矩阵的求法。对矩阵可逆性的判断与逆矩阵的求法将会给矩阵的学习带来很大的帮助。
软件的解法,同时也讨论了广义逆矩阵的求法。对矩阵可逆性的判断与逆矩阵的求法将会给矩阵的学习带来很大的帮助。
第1章 矩 阵
1.1矩阵的定义
定义1 由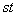 个数
个数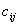 排成一个
排成一个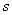 行
行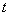 列的表
列的表
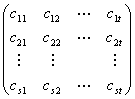
叫作一个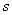 行
行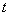 列(或
列(或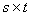 )矩阵,
)矩阵,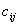 叫作这个矩阵的元素。
叫作这个矩阵的元素。
定义2 矩阵的行(列)初等变换指的是对一个矩阵施行的下列变换:
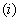 交换矩阵的两行(列);
交换矩阵的两行(列);
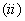 用一个不等于零的数乘矩阵的某一行(列),即用一个不等于零的数乘矩阵的某一行(列)的元素;
用一个不等于零的数乘矩阵的某一行(列),即用一个不等于零的数乘矩阵的某一行(列)的元素;
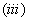 用某一数乘矩阵的某一行(列)后加到另一行(列),即用某一数乘矩阵的某一行(列)的每一元素后加到另一行(列)的对应元素上。
用某一数乘矩阵的某一行(列)后加到另一行(列),即用某一数乘矩阵的某一行(列)的每一元素后加到另一行(列)的对应元素上。
矩阵的初等变换在线性方程组求解,求矩阵的秩及求矩阵的逆矩阵方面都有重要的作用。
1.2矩阵运算
定义1 数域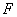 的数
的数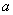 与
与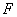 上一个
上一个 矩阵
矩阵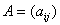 的乘积
的乘积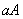 指的是
指的是 矩阵
矩阵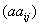 ,求数与矩阵的乘积的运算叫作数与矩阵的乘法。
,求数与矩阵的乘积的运算叫作数与矩阵的乘法。
定义2 两个 矩阵
矩阵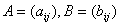 的和
的和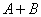 指的是
指的是 矩阵
矩阵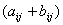 ,求两个矩阵的和的运算叫作矩阵的加法。
,求两个矩阵的和的运算叫作矩阵的加法。
要注意,我们只能把行数与列数都对应相同的两个矩阵相加。
由定义1和2,容易推出以下规律:
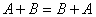
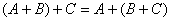
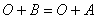


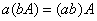
这里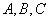 表示任意
表示任意 矩阵,而
矩阵,而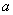 和
和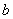 表示
表示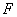 中的任意数。
中的任意数。
定义3 数域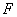 上
上 矩阵
矩阵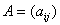 与
与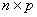 矩阵
矩阵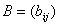 的乘积
的乘积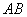 指的是一个
指的是一个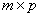 矩阵,这个矩阵的第
矩阵,这个矩阵的第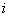 行第
行第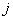 列的元素
列的元素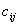 等于
等于 的第
的第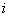 行的元素与
行的元素与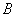 的第
的第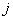 列的对应元素的乘积的和:
列的对应元素的乘积的和:

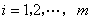 ,
,
矩阵的乘法的结合律:
矩阵的乘法和加法满足分配律: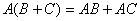
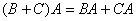
矩阵的乘法和数域矩阵的乘法: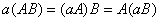
特别注意:矩阵的乘法不满足交换律。
一个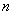 阶方阵
阶方阵 的
的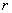 次方有意义:
次方有意义:
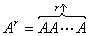
我们再约定
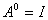
定义4 设 矩阵
矩阵
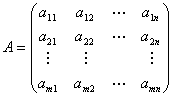
把 的行变为列所得到的
的行变为列所得到的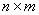 阶矩阵
阶矩阵
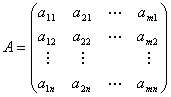
叫作矩阵 的转置。
的转置。
矩阵的转置满足以下规律:
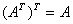
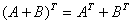
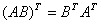

第2章 矩阵的可逆性及逆矩阵
2.1矩阵的基本概念
定义 令 是数域
是数域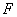 上一个
上一个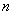 阶矩阵。若是存在
阶矩阵。若是存在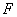 上
上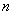 阶矩阵
阶矩阵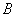 ,使得
,使得
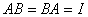
那么 叫作一个可逆矩阵(或非奇异矩阵),而
叫作一个可逆矩阵(或非奇异矩阵),而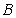 叫作
叫作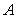 的逆矩阵。
的逆矩阵。
下面的几个概念有助于对矩阵可逆性及逆矩阵求法理解:
(1)设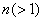 阶矩阵
阶矩阵
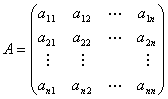
以下等式成立:
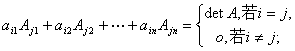
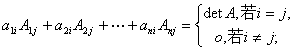
这里 是行列式
是行列式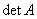 中元素
中元素 的代数余子式。
的代数余子式。
由此 若是设
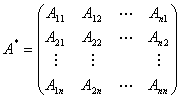
那么

我们把矩阵 叫作矩阵
叫作矩阵 的伴随矩阵。
的伴随矩阵。
(2)初等矩阵:对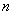 阶单位矩阵
阶单位矩阵 做一次初等变换所得到的矩阵:
做一次初等变换所得到的矩阵:

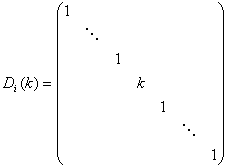
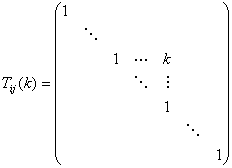
将这三种方阵叫作初等矩阵。通过验算容易看出初等矩阵都是可逆的,并且它们的逆矩阵仍是初等矩阵。
2.2矩阵可逆性的判断方法
依照不同的方式和性质,可以从下列几方面来判断矩阵的可逆性:
(1)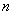 阶矩阵
阶矩阵 可逆当且仅当它可以写成初等矩阵的乘积。
可逆当且仅当它可以写成初等矩阵的乘积。
证明: 可以通过初等变换化为单位矩阵
可以通过初等变换化为单位矩阵 ,就是说,
,就是说, 可以通过初等变换化为
可以通过初等变换化为 ,也就是说,存在初等矩阵
,也就是说,存在初等矩阵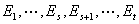 ,使
,使
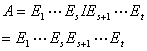
这是由初等矩阵的逆矩阵还是初等矩阵的性质推出的。
例1.用初等矩阵表示下面的方阵
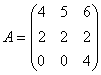
解:根据左行右列的规律:
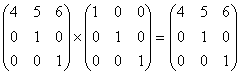

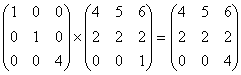
故矩阵 
(2)若矩阵行列式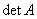 不为零,则其矩阵
不为零,则其矩阵 可逆。
可逆。
证明:将矩阵 分解为
分解为
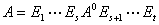
其中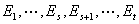 是初等矩阵,
是初等矩阵,
由初等矩阵的性质可以知道,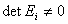 及矩阵乘积的行列式等于其各自行列式的乘积 及得
及矩阵乘积的行列式等于其各自行列式的乘积 及得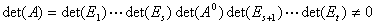 ,所以矩阵行列式
,所以矩阵行列式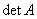 不为零时,其矩阵
不为零时,其矩阵 可逆。
可逆。
综上所述:行列式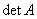 不为零,则其矩阵
不为零,则其矩阵 可逆。
可逆。
例2.判断下列矩阵是否可逆。
(1)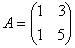 (2)
(2) 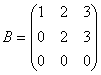
解:(1) 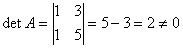 ,所以
,所以 可逆。
可逆。
(2) 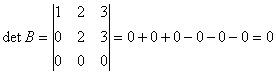 ,所以
,所以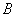 不可逆。
不可逆。
(3)含有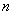 个坐标的
个坐标的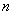 个向量组成的方阵
个向量组成的方阵 ,若这
,若这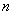 个向量线性无关,则这个方阵
个向量线性无关,则这个方阵 是可逆。
是可逆。
证明:设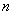 个向量分别是
个向量分别是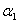 ,
,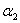 ,…,
,…,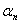
且 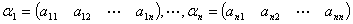 ,
,
则 这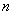 个向量构成了一个
个向量构成了一个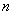 阶方阵,
阶方阵,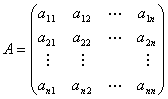
将矩阵 化为
化为 
若其中有一个或者一个以上的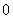 ,则向量
,则向量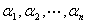 ,可以化为
,可以化为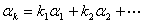
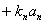 即
即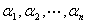 向量是线性相关的一个矩阵。
向量是线性相关的一个矩阵。
与条件相矛盾。即矩阵 可以化为单位矩阵,所以方阵可逆。
可以化为单位矩阵,所以方阵可逆。
例3. 令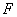 是任意的一个数域。
是任意的一个数域。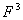 中判断向量
中判断向量
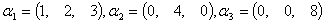
的相关性,由此判断其构成的矩阵 的可逆性。
的可逆性。
解:设存在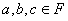 ,使得
,使得

即 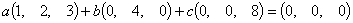
因而有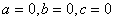 ,则
,则 线性无关。则表明
线性无关。则表明 中得任意一个都不能被另外两个表示。则其构成的矩阵
中得任意一个都不能被另外两个表示。则其构成的矩阵

通过化简后每一行或列都含有一个数,及其行列式不为零。
(4)设一个齐次线性方程组的系数矩阵 是一个方阵,若此齐次线性方程组仅有零解,则我们可以判定这个方阵
是一个方阵,若此齐次线性方程组仅有零解,则我们可以判定这个方阵 可逆。
可逆。
证明:矩阵来表示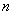 个
个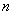 元齐次方程组:
元齐次方程组: 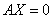
因为齐次线性方程组的变换中只有行变换,故不改变系数矩阵的可逆性。而只有零解使其行列式的秩等于其行数和列数。一个方阵构成的线性方程组若只有零解,则这个矩阵 可逆;若其有非零解,则矩阵
可逆;若其有非零解,则矩阵 不可逆。
不可逆。
例4. 矩阵 是一个齐次线性方程组系数矩阵,证明矩阵
是一个齐次线性方程组系数矩阵,证明矩阵 可逆。
可逆。
证明:构造齐次线性方程组: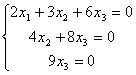 化简后得,
化简后得,
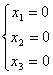
即此齐次方程组只有零解,故矩阵 可逆。
可逆。
我们常常用方阵来解线性方程组,这种转换的方式可以使我们更好的理解矩阵的实质。
(5)设 与
与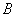 都是
都是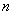 阶矩阵,证明:若
阶矩阵,证明:若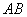 可逆,则
可逆,则 和
和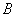 都可逆;反之也对。
都可逆;反之也对。
证明:因为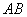 可逆,则
可逆,则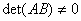 由
由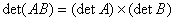 ,得
,得 ,
,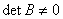 ,
, 和
和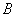 都可逆 。
都可逆 。
(6)设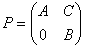 是一个n阶正方阵并且
是一个n阶正方阵并且 ,
,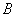 分别为
分别为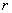 和
和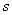 阶可逆方阵
阶可逆方阵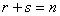 ,
,
则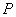 是可逆矩阵 并且
是可逆矩阵 并且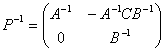
证明:我们由例(1)知道,方阵 是由
是由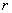 个无关向量构成的,
个无关向量构成的,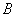 是由
是由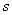 个无关向量构成的,则
个无关向量构成的,则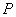 则是由个
则是由个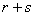 无关向量构成的,有
无关向量构成的,有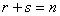 ,得
,得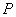 是秩为
是秩为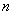 的
的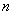 阶方阵。则
阶方阵。则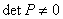 ,所以
,所以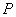 可逆。
可逆。
2.3 逆矩阵的求法
在判断一个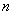 阶矩阵
阶矩阵 可逆后,就可以求其逆矩阵。主要求逆矩阵的方法有:
可逆后,就可以求其逆矩阵。主要求逆矩阵的方法有:
1.利用初等行变换求逆矩阵。
如果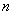 阶矩阵
阶矩阵 可逆,要求
可逆,要求 的逆矩阵,首先由
的逆矩阵,首先由 作出一个
作出一个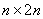 矩阵,即
矩阵,即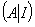 ,其次对这个矩阵施以行初等变换,将它的左半部的矩阵
,其次对这个矩阵施以行初等变换,将它的左半部的矩阵 化为单位矩阵,那么右半部的单位矩阵就同时化为
化为单位矩阵,那么右半部的单位矩阵就同时化为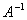 :
:
例5.求矩阵 的逆矩阵
的逆矩阵
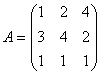
解: 先判断矩阵 是否可逆,矩阵
是否可逆,矩阵 行列式
行列式
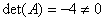
写下 ,并把单位矩阵
,并把单位矩阵 写在
写在 的右边:
的右边:
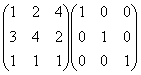
实行行的初等变换把 变成
变成 ,但是要记得每次对右边的矩阵施行同样的初等变换。
,但是要记得每次对右边的矩阵施行同样的初等变换。
第二行和第三行分别减去第一行的3倍和第一行,得
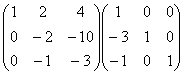
用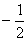 乘以第二行,得
乘以第二行,得
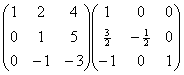
第三行加上第二行,得
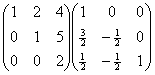
第三行除以2,得
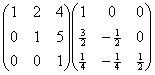
第二行加上第三行的-5倍,第一行加上第三行的-4倍,得
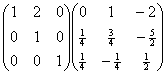
第一行加上第二行的-2倍,得
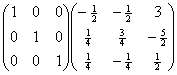
验证得: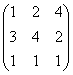
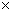
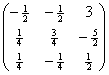

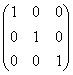
这种方法求逆矩阵的过程清晰易懂,是求逆矩阵的基本方法。
2.利用初等列变换求逆矩阵。
如果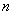 阶矩阵
阶矩阵 可逆,作一个
可逆,作一个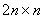 的矩阵
的矩阵 ,然后对此矩阵施以初等列变换,使矩阵
,然后对此矩阵施以初等列变换,使矩阵 化为单位矩阵
化为单位矩阵 ,则同时
,则同时 即化为
即化为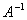 ,即
,即
例6.求矩阵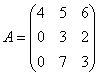 的逆矩阵。
的逆矩阵。
解: 先判断矩阵 是否可逆,矩阵
是否可逆,矩阵 行列式
行列式 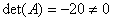
写下 ,并把单位矩阵
,并把单位矩阵 写在
写在 的下边:
的下边:
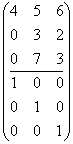
实行列初等变换把 变成
变成 ,但是要记得每次对下边的矩阵施行同样的初等变换。第一列除以4,
,但是要记得每次对下边的矩阵施行同样的初等变换。第一列除以4,
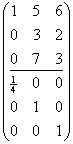
用第一列乘以-5加到第二列,用第一列乘以-6加到第三列,
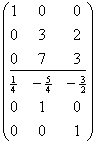
第二列除以3,
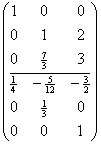
用第二列乘以-2加到第三列,
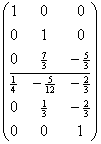
第三列乘以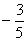 ,
,
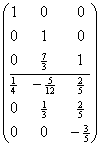
用第三列乘以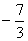 加到第二列,
加到第二列,
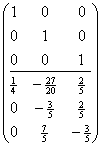
验证得: 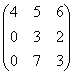
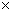
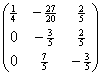


3.利用矩阵的伴随矩阵求逆矩阵。
定理:矩阵 可逆当且仅当矩阵
可逆当且仅当矩阵 行列式
行列式 且
且 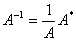
证明:必要性:由 可逆,即存在
可逆,即存在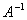 ,使
,使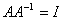 ,故
,故
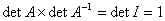
所以 
充分性:因为 
由于 ,所以
,所以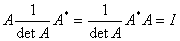
由可逆的定义有
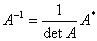
这种求逆矩阵的方法计算量很大,理论上的作用较为重要的。
例 7. 下列矩阵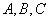 是否可逆,若可逆,求出其逆矩阵。
是否可逆,若可逆,求出其逆矩阵。
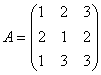 ,
,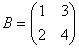 ,
,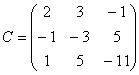
解: 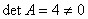 ,故
,故 可逆
可逆
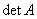 中各元素的代数余子式为,
中各元素的代数余子式为, 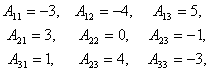
所以
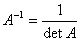
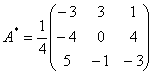
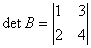 =-2
=-2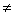 0,所以矩阵
0,所以矩阵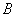 可逆。即
可逆。即
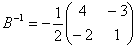
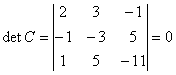 ,所以矩阵
,所以矩阵 不可逆。
不可逆。
4.分块矩阵求逆矩阵。
分块矩阵法是针对高阶矩阵的一种解法。首先我们要判断怎样对矩阵做分快更合适求逆矩阵,尽量使各分块矩阵求逆的运算更简便,从而简化原矩阵求逆。
例8. 求矩阵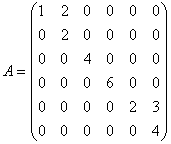 的逆矩阵。
的逆矩阵。
解:将矩阵 分成四块
分成四块 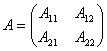
其中 ,
,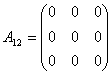 ,
,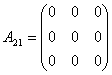 ,
,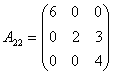
根据矩阵的乘法性质: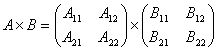
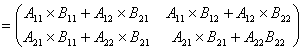
要使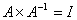 ,即要使
,即要使
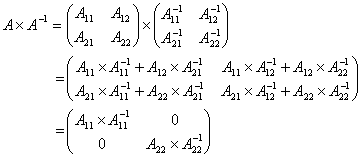
由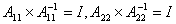
求得 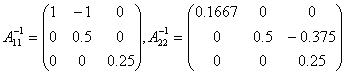
故所求逆矩阵是 
验证: 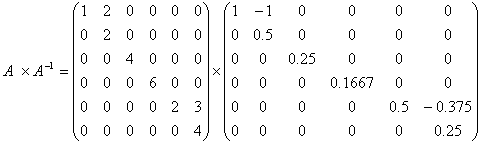

5.求解逆矩阵也可以用计算机软件来做。其步骤是先输入一个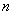 阶矩阵
阶矩阵 ,然后判断它的行列式是否为零,再用
,然后判断它的行列式是否为零,再用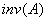 ,即可得到你需要的逆矩阵。
,即可得到你需要的逆矩阵。
下例就是用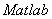 软件的解法求逆矩阵:
软件的解法求逆矩阵:
例9. 求矩阵 的逆矩阵
的逆矩阵
 =
=
解:

即 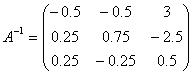
第3章 可逆性的拓展——广义逆矩阵
3.1广义逆矩阵的引入
1920年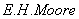 利用正交投影算子首次引入广义逆矩阵的概念,但未引起人们的注意。到1955年
利用正交投影算子首次引入广义逆矩阵的概念,但未引起人们的注意。到1955年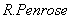 通过线性方程组的研究来定义广义逆矩阵,这才受到关注。以后广义逆矩阵的研究得到迅速发展,并逐步在系统理论、优化问题和控制理论等许多领域中被广泛地应用。后来证明
通过线性方程组的研究来定义广义逆矩阵,这才受到关注。以后广义逆矩阵的研究得到迅速发展,并逐步在系统理论、优化问题和控制理论等许多领域中被广泛地应用。后来证明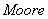 与
与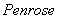 的定义方法,这就是:
的定义方法,这就是:
设 矩阵
矩阵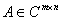 ,如果存在
,如果存在 矩阵
矩阵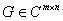 ,满足
,满足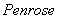 条件的一部分或全部:
条件的一部分或全部:
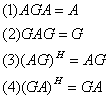
则称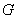 为
为 的一个广义逆矩阵。
的一个广义逆矩阵。
3.2广义逆矩阵的定义及存在性
定义 设 矩阵
矩阵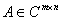 ,如果存在
,如果存在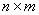 矩阵
矩阵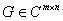 满足条件
满足条件
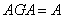
则称为矩阵的广义逆矩阵,并记做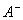 。
。
值得注意对于任何矩阵 ,这样的
,这样的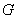 并不唯一,这一点从本例可见到:
并不唯一,这一点从本例可见到:
若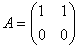 ,则有
,则有 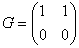 ,都有
,都有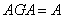 ,同时对任意的
,同时对任意的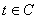 ,每个矩阵
,每个矩阵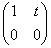 都可作为
都可作为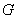 ,使得
,使得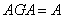 也成立。
也成立。
因此,对任何矩阵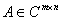 ,就定义
,就定义 的广义逆矩阵集:
的广义逆矩阵集:
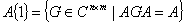
并且集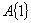 中任何一个矩阵
中任何一个矩阵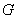 都可以记为
都可以记为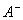 。
。
例10.求矩阵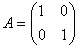 的广义逆矩阵。
的广义逆矩阵。
解: 由定义知,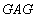 =
= ,设
,设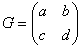 ,有
,有
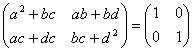
故 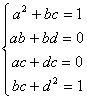
若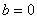 时,有
时,有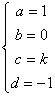 或
或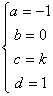 ,其中
,其中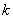 为任意的常数;
为任意的常数;
若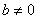 时,有
时,有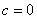 ,
,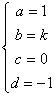 或
或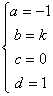 其中
其中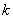 为任意的常数;
为任意的常数;
有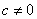 ,
,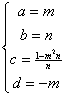 其中
其中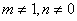 的任意常数。
的任意常数。
定理:设 矩阵
矩阵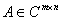 ,秩
,秩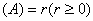 且有可逆矩阵
且有可逆矩阵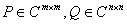
使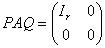 ,则
,则 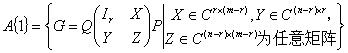
证明:由题设知
现在任取 ,应有
,应有 ,即要求:
,即要求:
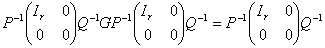
将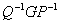 作分块形式, 即
作分块形式, 即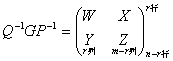
并代入上式就推出
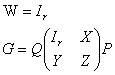
反之,任取这样的一个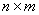 矩阵
矩阵 ,则有
,则有
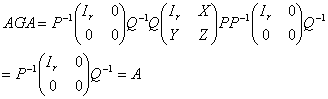
故证得。
由本定理可得,当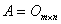 时,则
时,则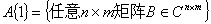 ;对
;对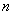 阶非奇异矩阵
阶非奇异矩阵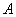 ,因存在
,因存在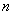 阶可逆矩阵
阶可逆矩阵 和
和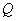 ,使得
,使得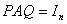 ,即
,即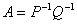 ,则有
,则有
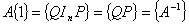
这说明 非奇异家族中对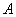 的广义逆矩阵
的广义逆矩阵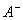 是唯一的,即为
是唯一的,即为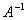 。
。
例11.设矩阵
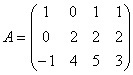 求
求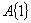 ,并给出一个
,并给出一个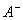 。
。
解:为得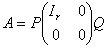 中的
中的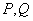 ,对下列矩阵施行初等行变换及初等列变换,化为
,对下列矩阵施行初等行变换及初等列变换,化为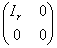 形式,即
形式,即
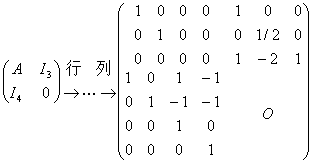
于是
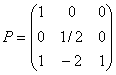
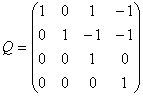
因此

并且当令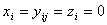 时,就得一个最简单的
时,就得一个最简单的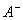 如下:
如下:
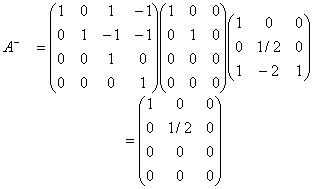
关于广义逆矩阵的求法和应用还有待更深入的探究,特别是它与具体矩阵的逆矩阵的联系更有学习的意义。
第4章 总结
本文主要讨论了矩阵可逆的判定条件和求逆矩阵的基本方法。矩阵可逆性是矩阵乘法运算的逆运算类似数的除法运算的前提,求可逆矩阵的逆矩阵的方法主要就是两类:一类是以矩阵的初等变换为基础的方法,是求逆矩阵的一般方法,并且可以推广到分块矩阵去解决高阶三角形的矩阵求逆。另一类就是利用矩阵与其伴随矩阵的乘积,加上行列式的依行依列展开式的性质来求矩阵的逆矩阵的方法,此类方法主要是理论作用较大,而具体求逆矩阵的计算量太大,不易对高阶矩阵求逆。随着社会的进步和发展,计算机中在处理大的数据时,常运用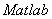 计算方法得出我们需要的结果,避免了在数学计算中的复杂性,这给矩阵理论的深入研究和实际应用提供了发展空间,同时也需要我们进一步的学习和探究。
计算方法得出我们需要的结果,避免了在数学计算中的复杂性,这给矩阵理论的深入研究和实际应用提供了发展空间,同时也需要我们进一步的学习和探究。
参考文献
【1】张禾瑞、郝鈵新. 高等代数[M]第五版.北京:高等教育出版社. 20##年
【2】杜之韩 刘丽 吴曦.线性代数[M]第三版.成都:西南财经大学出版社. 20##年
【3】陈治中.线性代数[M].北京:科学出版社. 20##年
【4】董霖. 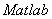 使用详解[M].北京:科学出版社. 20##年
使用详解[M].北京:科学出版社. 20##年
【5】魏洪增.矩阵理论与方法[M]. 北京:电子工业出版社. 20##年
