抛物线的标准方程、图象及几何性质:p?0
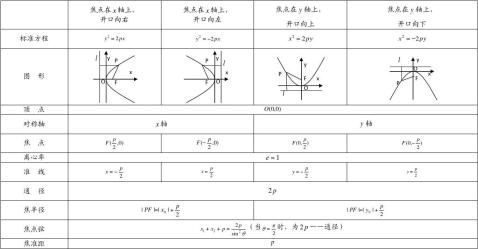
关于抛物线知识点的补充:
1、定义:
2、几个概念:
① p的几何意义:焦参数p是焦点到准线的距离,故p为正数;
② 焦点的非零坐标是一次项系数的14
③ 方程中的一次项的变量与对称轴的名称相同,一次项的系数符号决定抛物线的开口方向。 ④ 通径:2p
3、如:AB是过抛物线y2?2px(p?0)焦点F的弦,M是AB的中点,l是抛物线的准线,MN?l,
为垂足,求证:
(1)HF?DF; (2)AN?BN; (3)FN?AB; (4)设MN交抛物线于Q,则Q平分MN; (5)设A(x1,y1),B(x2,y2),则y1y2??p2,x1
1x2?4p2;
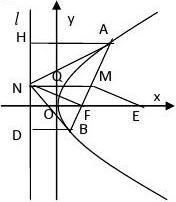
N为垂足,BD?l,AH?l,D,H
(6)1?1?2; |FA||FB|p
(7)A,O,D三点在一条直线上
(8)过M作ME?AB,ME交x轴于E,求证:|EF|?1|AB|,|ME|2?|FA|?|FB|; 2
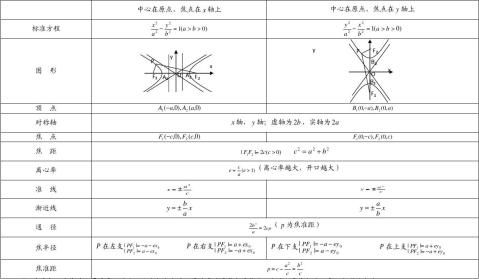
关于双曲线知识点的补充:
1、 双曲线的定义:平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹。 e(e?1)的点的轨迹。两个定点为双曲线的焦点,焦点间距离叫做焦距;定直线叫做准线。常数叫做离心率。
注意: |PF1|?|PF2|?2a与|PF2|?|PF1|?2a(2a?|F1F2|)表示双曲线的一支。 2a?|F1F2|表示两条射线;2a?|F1F2|没有轨迹;
2、 双曲线的标准方程
x2y2y2x2
①焦点在x轴上的方程:2?2?1(a>0,b>0); ②焦点在y轴上的方程:2?2?1 (a>0,b>0); abab
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2-ny2=1(m〃n<0);
④双曲线的渐近线:改1为0,分解因式则可得两条渐近线之方程.
3、双曲线的渐近线: ①求双曲线x
a22?y?1的渐近线,可令其右边的2b21为0,即得x2a2?y
b22x2y2?0,因式分解得到。②与双曲线2?2?1共渐近线的双曲线系方程是ab
x2y2
???; a2b2
4、等轴双曲线: 为x2?y2?t2,其离心率为2
5、共轭双曲线:
6、几个概念:
b22b2?x2y2
22③等轴双曲线x-y=? (?∈R,?≠0):渐近线是y=±x,2 ;④2?2?1焦点三角形的面积:b2cotca2ab
(其中∠F1PF2=?);
⑤弦长公式:
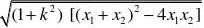
|AB|=c2=a2-b2,而在双曲线中:c2=a2+b2,
8、双曲线中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法?是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法?是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法?根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式再得出参数的变化范围;第二种是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围。 关于椭圆知识点的补充: 1、椭圆的标准方程:
x2y2y2x2
① 焦点在x轴上的方程:2?2?1 (a>b>0); ②焦点在y轴上的方程:2?2?1 (a>b>0);
abab
?x?acos?
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2+ny2=1(m>0,n>0); ④、参数方程:?
?y?bsin?2、椭圆的定义:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹。
|PF1|
e(0?e?1)椭圆的焦半径公式:|PF1|=a+ex0,
d|PF2|=a-ex0)其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。 常数叫做离心率。 注意: 2a?|F1F2|表示椭圆;2a?|F1F2|表示线段F1F2;2a?|F1F2|没有轨迹;
b22b2?x2y2
3、 焦准距:、通径:、点与椭圆的位置关系; 6、2?2?1焦点三角形的面积:b2tan (其中∠F1PF2=?);
ca2ab7、弦长公式:
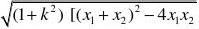
8、 椭圆在点P(x0,y0)处的切线方程:
x0xy0y
?2?1; 2ab
9、直线与椭圆的位置关系:
凡涉及直线与椭圆的问题,通常设出直线与椭圆的方程,将二者联立,消去x或y,得到关于y或x的一元二次方程,再利用根与系数的关系及根的判别式等知识来解决,需要有较强的综合应用知识解题的能力。 10、椭圆中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法?是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法?是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法?根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围;第二种?是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围
椭圆图象及几何性质:


第二篇:解析几何综合题解题方法总结
解析几何综合题解题方法总结
富源县第一中学
解析几何综合题是高考命题的热点内容之一. 这类试题往往以解析几何知识为载体,综合函数、不等式、三角、数列等知识,所涉及到的知识点较多,对解题能力考查的层次要求较高,考生在解答时,常常表现为无从下手,或者半途而废。据此笔者认为:解决这一类问题的关键在于:通观全局,局部入手,整体思维. 即在掌握通性通法的同时,不应只形成一个一个的解题套路,解题时不加分析,跟着感觉走,做到那儿算那儿. 而应当从宏观上去把握,从微观上去突破,在审题和解题思路的整体设计上下功夫,不断克服解题征途中的道道运算难关.
一、判别式
案例1 已知双曲线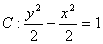 ,直线
,直线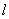 过点
过点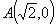 ,斜率为
,斜率为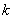 ,当
,当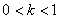 时,双曲线的上支上有且仅有一点B到直线
时,双曲线的上支上有且仅有一点B到直线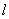 的距离为
的距离为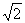 ,试求
,试求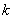 的值及此时点B的坐标。
的值及此时点B的坐标。
分析1:解析几何是用代数方法来研究几何图形的一门学科,因此,数形结合必然是研究解析几何问题的重要手段. 从“有且仅有”这个微观入手,对照草图,不难想到:过点B作与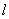 平行的直线,必与双曲线C相切. 而相切的代数表现形式是所构造方程的判别式
平行的直线,必与双曲线C相切. 而相切的代数表现形式是所构造方程的判别式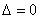 . 由此出发,可设计如下解题思路:
. 由此出发,可设计如下解题思路:

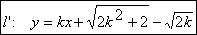

解题过程略.
分析2:如果从代数推理的角度去思考,就应当把距离用代数式表达,即所谓“有且仅有一点B到直线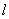 的距离为
的距离为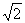 ”,相当于化归的方程有唯一解. 据此设计出如下解题思路:
”,相当于化归的方程有唯一解. 据此设计出如下解题思路:
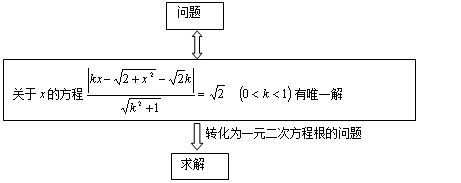
简解:设点 为双曲线C上支上任一点,则点M到直线
为双曲线C上支上任一点,则点M到直线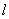 的距离为:
的距离为:
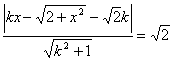


于是,问题即可转化为如上关于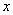 的方程.
的方程.
由于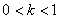 ,所以
,所以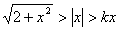 ,从而有
,从而有
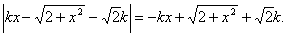
于是关于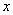 的方程
的方程



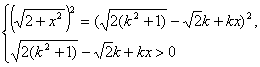


由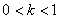 可知:
可知:
方程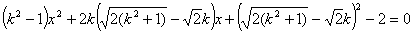 的二根同正,故
的二根同正,故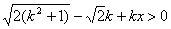 恒成立,于是
恒成立,于是 等价于
等价于
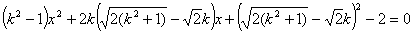 .
.
由如上关于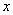 的方程有唯一解,得其判别式
的方程有唯一解,得其判别式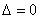 ,就可解得
,就可解得  .
.
点评:上述解法紧扣解题目标,不断进行问题转换,充分体现了全局观念与整体思维的优越性.
2 判别式与韦达定理
例2 .已知椭圆C: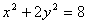 和点P(4,1),过P作直线交椭圆于A、B两点,在线段AB上取点Q,使
和点P(4,1),过P作直线交椭圆于A、B两点,在线段AB上取点Q,使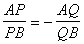 ,求动点Q的轨迹所在曲线的方程.
,求动点Q的轨迹所在曲线的方程.
分析:这是一个轨迹问题,解题困难在于多动点的困扰,学生往往不知从何入手。其实,应该想到轨迹问题可以通过参数法求解. 因此,首先是选定参数,然后想方设法将点Q的横、纵坐标用参数表达,最后通过消参可达到解题的目的.
由于点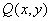 的变化是由直线AB的变化引起的,自然可选择直线AB的斜率
的变化是由直线AB的变化引起的,自然可选择直线AB的斜率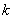 作为参数,如何将
作为参数,如何将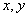 与
与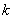 联系起来?一方面利用点Q在直线AB上;另一方面就是运用题目条件:
联系起来?一方面利用点Q在直线AB上;另一方面就是运用题目条件: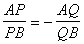 来转化.由A、B、P、Q四点共线,不难得到
来转化.由A、B、P、Q四点共线,不难得到 ,要建立
,要建立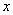 与
与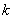 的关系,只需将直线AB的方程代入椭圆C的方程,利用韦达定理即可.
的关系,只需将直线AB的方程代入椭圆C的方程,利用韦达定理即可.
通过这样的分析,可以看出,虽然我们还没有开始解题,但对于如何解决本题,已经做到心中有数.
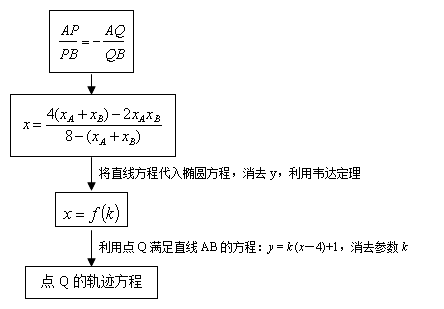
在得到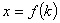 之后,如果能够从整体上把握,认识到:所谓消参,目的不过是得到关于
之后,如果能够从整体上把握,认识到:所谓消参,目的不过是得到关于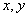 的方程(不含k),则可由
的方程(不含k),则可由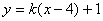 解得
解得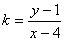 ,直接代入
,直接代入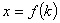 即可得到轨迹方程。从而简化消去参的过程。
即可得到轨迹方程。从而简化消去参的过程。
简解:设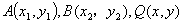 ,则由
,则由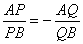 可得:
可得: ,
,
解之得: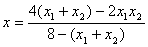 (1)
(1)
设直线AB的方程为: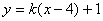 ,代入椭圆C的方程,消去
,代入椭圆C的方程,消去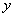 得出关于 x的一元二次方程:
得出关于 x的一元二次方程:
 (2)
(2)
∴ 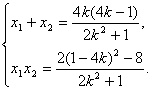
代入(1),化简得: (3)
(3)
与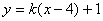 联立,消去
联立,消去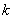 得:
得: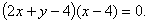
在(2)中,由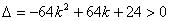 ,解得
,解得 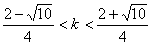 ,结合(3)可求得
,结合(3)可求得 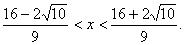
故知点Q的轨迹方程为: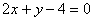 (
( ).
).
点评:由方程组实施消元,产生一个标准的关于一个变量的一元二次方程,其判别式、韦达定理模块思维易于想到. 这当中,难点在引出参,活点在应用参,重点在消去参.,而“引参、用参、消参”三步曲,正是解析几何综合问题求解的一条有效通道.
3 求根公式
例3. 设直线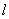 过点P(0,3),和椭圆
过点P(0,3),和椭圆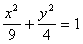 顺次交于A、B两点,试求
顺次交于A、B两点,试求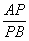 的取值范围.
的取值范围.
分析:本题中,绝大多数同学不难得到: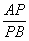 =
=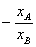 ,但从此后却一筹莫展, 问题的根源在于对题目的整体把握不够. 事实上,所谓求取值范围,不外乎两条路:其一是构造所求变量关于某个(或某几个)参数的函数关系式(或方程),这只需利用对应的思想实施;其二则是构造关于所求量的一个不等关系.
,但从此后却一筹莫展, 问题的根源在于对题目的整体把握不够. 事实上,所谓求取值范围,不外乎两条路:其一是构造所求变量关于某个(或某几个)参数的函数关系式(或方程),这只需利用对应的思想实施;其二则是构造关于所求量的一个不等关系.
分析1: 从第一条想法入手,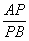 =
=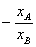 已经是一个关系式,但由于有两个变量
已经是一个关系式,但由于有两个变量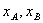 ,同时这两个变量的范围不好控制,所以自然想到利用第3个变量——直线AB的斜率k. 问题就转化为如何将
,同时这两个变量的范围不好控制,所以自然想到利用第3个变量——直线AB的斜率k. 问题就转化为如何将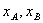 转化为关于k的表达式,到此为止,将直线方程代入椭圆方程,消去y得出关于
转化为关于k的表达式,到此为止,将直线方程代入椭圆方程,消去y得出关于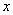 的一元二次方程,其求根公式呼之欲出.
的一元二次方程,其求根公式呼之欲出.
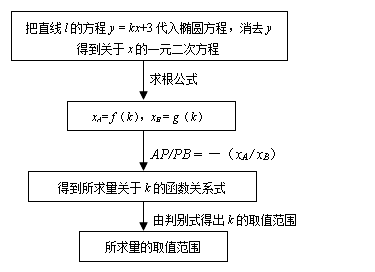
简解1:当直线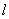 垂直于x轴时,可求得
垂直于x轴时,可求得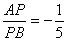 ;
;
当 与x轴不垂直时,设
与x轴不垂直时,设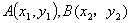 ,直线
,直线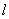 的方程为:
的方程为: ,代入椭圆方程,消去
,代入椭圆方程,消去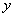 得
得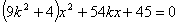 ,解之得
,解之得 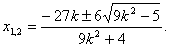
因为椭圆关于y轴对称,点P在y轴上,所以只需考虑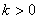 的情形.
的情形.
当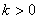 时,
时,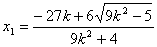 ,
,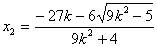 ,
,
所以 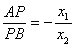 =
=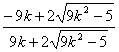 =
=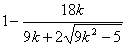 =
=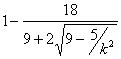 .
.
由 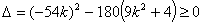 , 解得
, 解得 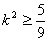 ,
,
所以 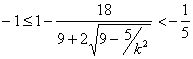 ,
,
综上 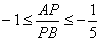 .
.
分析2: 如果想构造关于所求量的不等式,则应该考虑到:判别式往往是产生不等的根源. 由判别式值的非负性可以很快确定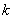 的取值范围,于是问题转化为如何将所求量与
的取值范围,于是问题转化为如何将所求量与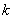 联系起来. 一般来说,韦达定理总是充当这种问题的桥梁,但本题无法直接应用韦达定理,原因在于
联系起来. 一般来说,韦达定理总是充当这种问题的桥梁,但本题无法直接应用韦达定理,原因在于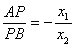 不是关于
不是关于 的对称关系式. 原因找到后,解决问题的方法自然也就有了,即我们可以构造关于
的对称关系式. 原因找到后,解决问题的方法自然也就有了,即我们可以构造关于 的对称关系式.
的对称关系式.
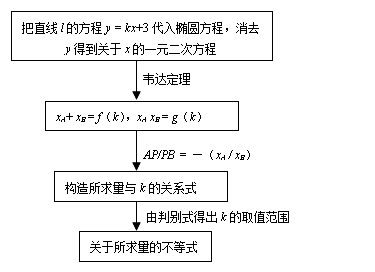
简解2:设直线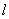 的方程为:
的方程为: ,代入椭圆方程,消去
,代入椭圆方程,消去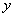 得
得
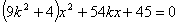 (*)
(*)
则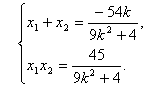 ,令
,令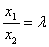 ,则,
,则,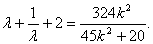
在(*)中,由判别式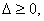 可得
可得 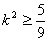 ,
,
从而有 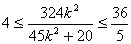 ,
,
所以  ,
,
解得  .
.
结合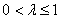 得
得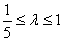 .
.
综上,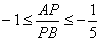 .
.
点评:范围问题不等关系的建立途径多多,诸如判别式法,均值不等式法,变量的有界性法,函数的性质法,数形结合法等等. 本题也可从数形结合的角度入手,给出又一优美解法.
解题犹如打仗,不能只是忙于冲锋陷阵,一时局部的胜利并不能说明问题,有时甚至会被局部所纠缠而看不清问题的实质所在,只有见微知著,树立全局观念,讲究排兵布阵,运筹帷幄,方能决胜千里.
