T091、
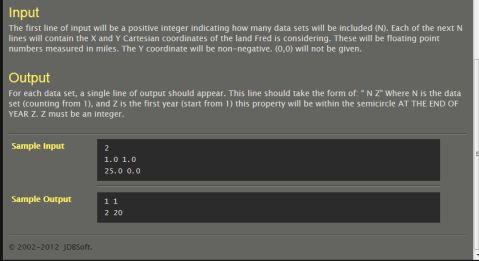
Houseboat
#include <stdio.h> #define PI 3.1415926 int main() {
int i,n;
double year,x,y; scanf("%d",&n); for(i=0;i<n;i++) {
scanf("%lf%lf",&x,&y);
year=PI*(x*x+y*y)/100;
printf("%d %d\n",i+1,(int)year+1); }
return 0;
}
T092、
Sticks
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int len[64], n, minlen, get;
bool b[64];
int cmp(const void *a, const void *b) {
return *(int *)a < *(int *)b ? 1 : -1; }
bool dfs(int nowlen, int nowget, int cnt) {
if(cnt >= n) return false;
if(get == nowget) return true;
int i;
bool f = false;
if(nowlen == 0) f = true;
for(i = cnt; i < n; i++)
{
if(!b[i])
{
if(len[i] + nowlen == minlen)
{
b[i] = true;
if(dfs(0, nowget+1, nowget))
return true;
b[i] = false;
return false;
}
else if(len[i] + nowlen < minlen)
{
b[i] = true;
if(dfs(nowlen+len[i], nowget, i+1)) return true;
b[i] = false;
if(f) return false;
while(i + 1 < n && len[i] == len[i+1]) i++; }
}
}
return false;
}
int main()
{
int i, tollen;
while(scanf("%d", &n), n)
{
tollen = 0;
int j = 0, p;
for(i = 0; i < n; i++)
{
scanf("%d", &p);
if(p <= 50)
{
len[j] = p;
tollen += len[j];
j++;
}
}
n = j;
if(n == 0)
{
printf("0\n");
continue;
}
qsort(len, n, sizeof(int), cmp); for(minlen = len[0]; ; minlen++) {
if(tollen % minlen) continue; memset(b, 0, sizeof(b)); get = tollen / minlen; if(dfs(0, 0, 0))
{
printf("%d\n", minlen); break;
}
}
}
return 0;
}
T093、
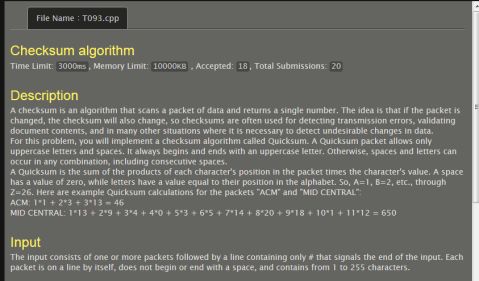
Checksum algorithm:
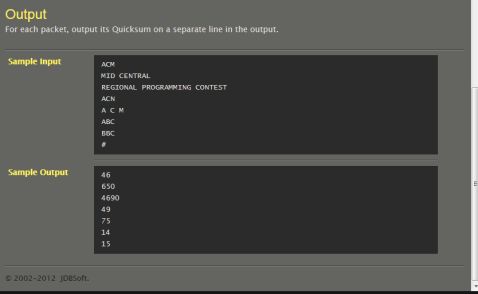
#include <stdio.h> int main()
{
char a[256];
int i,sum;
while(gets(a)&&a[0]!='#') {
sum=0;
for(i=0;a[i]!='\0';i++) if(a[i]!=' ')
sum+=(i+1)*(a[i]-64); printf("%d\n",sum); }
return 0;
}
T094、Bee:

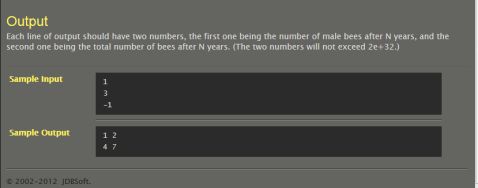
#include <stdio.h>
int main()
{
int n,a,b,sum,i,t;
while(scanf("%d",&n)!=EOF&&n!=-1) {
a=1,b=0,sum=0;
for(i=0;i<n;i++)
{
t=a;
a=b+1;
b=t+b;
sum=a+b;
}
printf("%d %d\n",b,sum);
}
return 0;
}
T095、Graveyard:
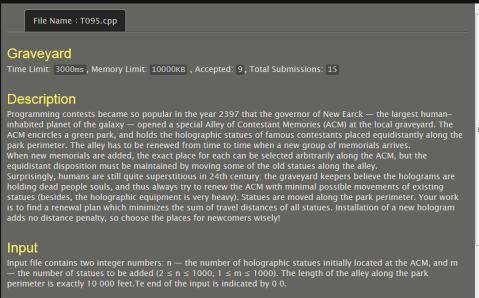
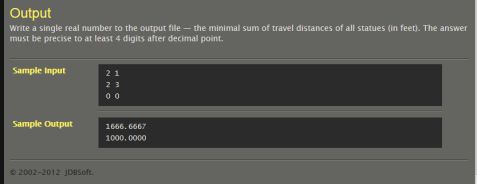
#include <stdio.h>
#include <math.h>
int main()
{
int n,m,i;
double s,a;
while((scanf("%d%d",&n,&m))!=EOF)
{
if(n==0&&m==0) break;
s=0;
for(i=1;i<n;i++)
{
a=i*1.0/n*(n+m);
s+=fabs(a-floor(a+0.5))/(n+m);/*放缩坐标系 floor(a+0.5))/(n+m) 找到离这个对应坐标的最近一个点 取得距离 累加移动距离 */ }
printf("%.4f\n",s*10000);
}
return 0;
}
T096、
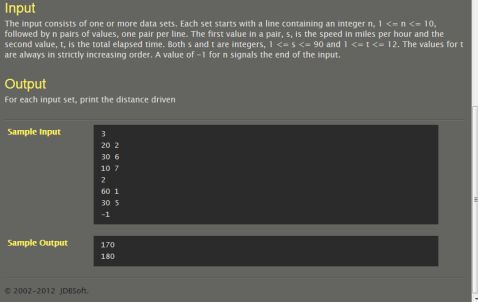
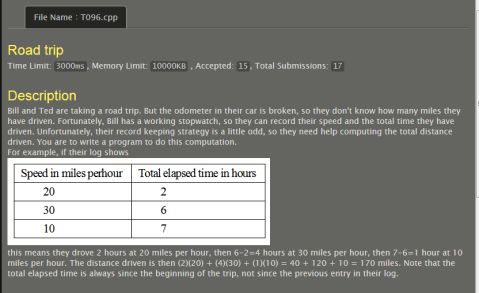
Road trip
#include<stdio.h>
int main()
{
int n,i,speed,hour,h,s;//s是路程,h是上次的时间 while(scanf("%d",&n) && n!=-1)
{
s=0;
h=0;
for(i=1;i<=n;i++)
{
scanf("%d %d",&speed,&hour); s+=speed*(hour-h);
h=hour;
}
printf("%d",s);
}
return 0;
}
T097、
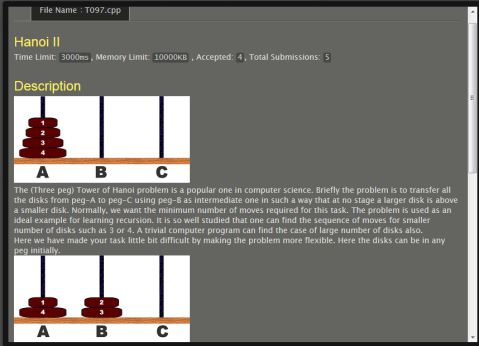
Hanoi II
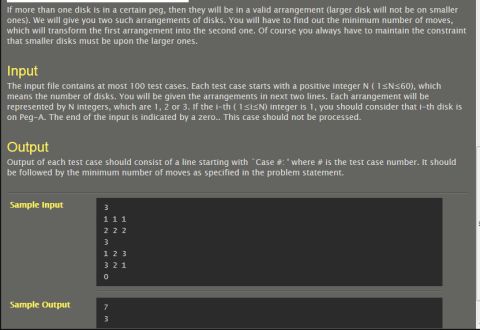
#include <stdio.h>
#define M 70
int start[M], targe[M];
long long f(int *p, int k, int fina)
{
if(k==0) return 0;
if(p[k]==fina) return f(p,k-1,fina);
return f(p,k-1,6-fina-p[k])+(1LL<<(k-1)); }
int main ()
{
long long ans;
int n, cas = 0;
while(scanf("%d",&n), n)
{
for(int i = 1; i <= n; i++) scanf("%d",&start[i]); for(int i = 1; i <= n; i++) scanf("%d",&targe[i]); int c = n;
for(;c>=1&&start[c]==targe[c];c--); if(c==0) {printf("0\n"); continue;}
int other = 6 - start[c] - targe[c];
ans = f(start,c-1,other)+f(targe,c-1,other)+1; printf("%lld\n",ans);
}
return 0;
}
T098、
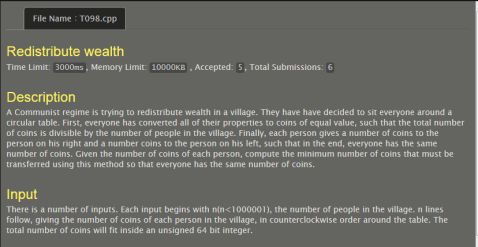
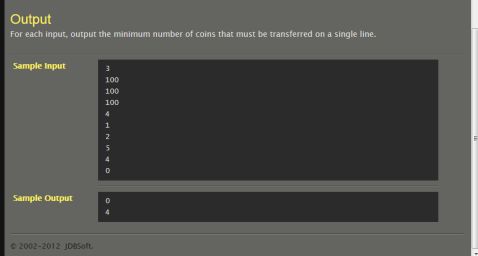
Redistribute wealth
#include <stdio.h> #include <math.h> #include <string.h> #include <stdlib.h>
long long money[1000001]; long long C[1000001]; int main()
{
int n,t,i,j;
while(scanf("%d",&n)==1) {
int i;
long long sum=0;
for(i = 1;i<=n;++i)
{
scanf("%lld",&money[i]); sum += money[i];
}
long long M = sum/n; C[1] = money[1] - M; C[0] = 0;
for(i = 2;i<=n-1;++i)
{ C[i] = C[i-1] + money[i] - M; }
for(i=0;i<n-1;i++)
for(j=0;j<n-1-i;j++) if(C[j]>C[j+1])
{
t=C[j];
C[j]=C[j+1];
C[j+1]=t;
}
long long mid = C[n/2]; long long sum1 = 0; for(i = 0;i<=n-1;++i) sum1 += abs(mid-C[i]); printf("%lld\n",sum1); }
return 0;
}
T099、Dexter need help:
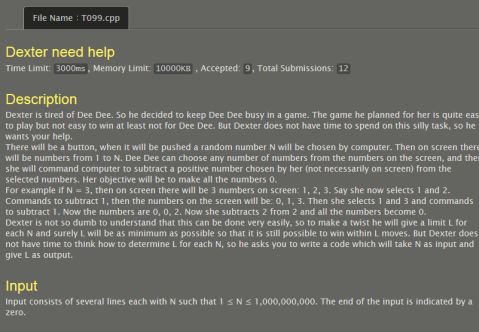
#include <stdio.h>
int fun(int a)
{
if(a==1) return 1;
else
return fun(a/2)+1;
}
int main()
{
int a,x;
while(scanf("%d",&a)&&a!=0) {
x=fun(a);
printf("%d\n",x); }
return 0;
}
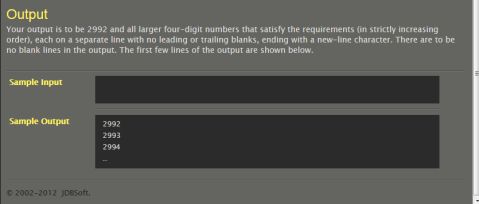
T100、
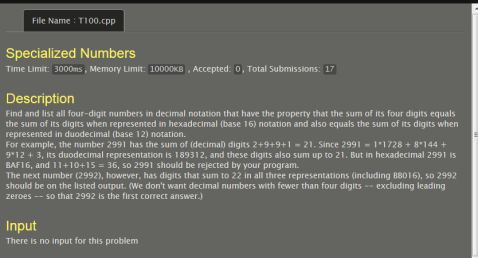
Specialized Numbers
#include <stdio.h> int fun(int i,int r) {
int s=0;
while(i)
{
s+=i%r;
i/=r;
}
return s;
}
int main()
{
int i;
for(i=2992;i<10000;i++)
if(fun(i,10)==fun(i,12)&&fun(i,12)==fun(i,16)) printf("%d\n",i);
return 0;
}
T100、Specialized Numbers
#include <stdio.h>
int fun(int i,int r)
{
int s=0;
while(i)
{
s+=i%r;
i/=r;
}
return s;
}
int main()
{
int i;
for(i=2992;i<10000;i++)
if(fun(i,10)==fun(i,12)&&fun(i,12)==fun(i,16)) printf("%d\n",i);
return 0;
}
(3)#include <stdio.h>
int main()
{
int i, n, sum10, sum12, sum16; for (i=2992; i<10000; i++){
n = i;
sum10 = 0;
while (n){
sum10 += n%10;
n /= 10;
}
n = i;
sum12 = 0;
while (n){
sum12 += n%12;
n /= 12;
}
n = i;
sum16 = 0;
while (n){
sum16 += n%16;
n /= 16;
}
if (sum10==sum12 && sum12==sum16) printf("%d\n", i); }
return 0;
}
第二篇:西工大C语言大作业习题答案
童鞋们,快来呀!
答案!答案!
no1.绘制余弦曲线
在屏幕上用“*”显示0~360度的余弦函数cos(x)曲线
*问题分析与算法设计
如果在程序中使用数组,这个问题十分简单。但若规定不能使用数组,问题就变得不容易了。
关键在于余弦曲线在0~360度的区间内,一行中要显示两个点,而对一般的显示器来说,只能按行输出,即:输出第一行信息后,只能向下一行输出,不能再返回到上一行。为了获得本文要求的图形就必须在一行中一次输出两个“*”。
为了同时得到余弦函数cos(x)图形在一行上的两个点,考虑利用cos(x)的左右对称性。将屏幕的行方向定义为x,列方向定义为y,则0~180度的图形与180~360度的图形是左右对称的,若定义图形的总宽度为62列,计算出x行0~180度时y点的坐标m,那么在同一行与之对称的180~360度的y点的坐标就应为62-m。程序中利用反余弦函数acos计算坐标(x,y)的对应关系。
使用这种方法编出的程序短小精炼,体现了一定的技巧。
*程序说明与注释
#include<stdio.h>
#include<math.h>
void main()
{
double y;
int x,m;
for(y=1;y>=-1;y-=0.1)
{
m=acos(y)*10;
for(x=1;x<m;x++) printf(" ");
printf("*");
for(;x<62-m;x++)printf(" ");
printf("*\\n");
}
}
no2.绘制余弦曲线和直线
在屏幕上显示0~360度的cos(x)曲线与直线f(x)=45*(y-1)+31的迭加图形。其中cos(x)图形用“*”表示,f(x)用“+”表示,在两个图形相交的点上则用f(x)图形的符号。
*问题分析与算法设计
本题可以在上题的基础上进行修改。图形迭加的关键是要在分别计算出同一行中两个图形的列方向点坐标后,正确判断相互的位置关系。为此,可以先判断图形的交点,再分别控制打印两个不同的图形。 *程序注释与说明
#include<stdio.h>
#include<math.h>
void main()
{
double y;
int x,m,n,yy;
for(yy=0;yy<=20;yy++)
{
y=0.1*yy;
m=acos(1-y)*10;
n=45*(y-1)+31;
for(x=0;x<=62;x++)
if(x==m&&x==n) printf("+");
else if(x==n) printf("+");
else if(x==m||x==62-m) printf("*");
else printf(" ");
printf("\\n");
}
}
--------------------------------------------------------------------------------
no3.绘制圆
在屏幕上用“*”画一个空心的圆
*问题分析与算法设计
打印圆可利用图形的左右对称性。根据圆的方程:
R*R=X*X+Y*Y
可以算出圆上每一点行和列的对应关系。
*程序说明与注释
#include<stdio.h>
#include<math.h>
void main()
{
double y;
int x,m;
for(y=10;y>=-10;y--)
{
m=2.5*sqrt(100-y*y);
for(x=1;x<30-m;x++) printf(" ");
printf("*");
for(;x<30+m;x++) printf(" ");
printf("*\\n");
}
}
no4.歌星大奖赛
在歌星大奖赛中,有10个评委为参赛的选手打分,分数为1~100分。选手最后得分为:去掉一个最高分和一个最低分后其余8个分数的平均值。请编写一个程序实现。
*问题分析与算法实现
这个问题的算法十分简单,但是要注意在程序中判断最大、最小值的变量是如何赋值的。
*程序说明与注释
#include<stdio.h>
void main()
{
int integer,i,max,min,sum;
max=-32768;
min=32767;
sum=0;
for(i=1;i<=10;i++)
{
printf("Input number %d=",i);
scanf("%d",&integer);
sum+=integer;
if(integer>max)max=integer;
if(integer<min)min=integer;
}
printf("Canceled max score:%d\\nCanceled min score:%d\\n",max,min);
printf("Average score:%d\\n",(sum-max-min)/8);
}
*运行结果
Input number1=90
Input number2=91
Input number3=93
Input number4=94
Input number5=90
Input number6=99
Input number7=97
Input number8=92
Input number9=91
Input number10=95
Canceled max score:99
Canceled min score:90
Average score:92
*思考题
题目条件不变,但考虑同时对评委评分进行裁判,即在10个评委中找出最公平(即评分最接返平均分)和最不公平(即与平均分的差距最大)的评委,程序应该怎样实现?
--------------------------------------------------------------------------------
no5.求最大数
问555555的约数中最大的三位数是多少?
*问题分析与算法设计
根据约数的定义,对于一个整数N,除去1和它自身外,凡能整除N的数即为N的约数。因此,最简单的方法是用2到N-1之间的所有数去除N,即可求出N的全部约数。本题只要求取约数中最大的三位数,则其取值范围可限制在100到999之间。
*程序说明与注释
#include<stdio.h>
void main()
{
long i;
int j;
printf("Please input number:");
scanf("%ld",&i);
for(j=999;j>=100;j--)
if(i%j==0)
{
printf("The max factor with 3 digits in %ld is:%d,\\n",i,j);
break;
}
}
*运行结果
输入:555555
输出:The max factor with 3 digits in 555555 is:777
no6.高次方数的尾数
求13的13次方的最后三位数
*问题分析与算法设计
解本题最直接的方法是:将13累乘13次方截取最后三位即可。
但是由于计算机所能表示的整数范围有限,用这种“正确”的算法不可能得到正确的结果。事实上,题目仅要求最后三位的值,完全没有必要求13的13次方的完整结果。
研究乘法的规律发现:乘积的最后三位的值只与乘数和被乘数的后三位有关,与乘数和被乘数的高位无关。利用这一规律,可以大大简化程序。
*程序说明与注释
#include<stdio.h>
void main()
{
int i,x,y,last=1;
printf("Input X and Y(X**Y):");
scanf("%d**%d",&x,&y);
for(i=1;i<=y;i++)
last=last*x%1000;
printf("The last 3 digits of %d**%d is:%d\\n",x,y,last%1000);
}
*运行结果
Input X and Y(X**Y):13**13
The last 3 digits of 13**13 is:253
Input X and Y(X**Y):13**20
The last 3 digits of 13**20 is:801
--------------------------------------------------------------------------------
no8.借书方案知多少
小明有五本新书,要借给A,B,C三位小朋友,若每人每次只能借一本,则可以有多少种不同的借法?
*问题分析与算法设计
本问题实际上是一个排列问题,即求从5个中取3个进行排列的方法的总数。首先对五本书从1至5进行编号,然后使用穷举的方法。假设三个人分别借这五本书中的一本,当三个人所借的书的编号都不相同时,就是满足题意的一种借阅方法。
*程序说明与注释
void main()
{
int a,b,c,count=0;
printf("There are diffrent methods for XM to distribute books to 3 readers:\\n"); for(a=1;a<=5;a++)
for(b=1;b<=5;b++)
for(c=1;a!=b&&c<=5;c++)
if(c!=a&&c!=b)
printf(count%8?"%2d:%d,%d,%d ":"%2d:%d,%d,%d\\n ",++count,a,b,c);
}
*运行结果
There are diffrent methods for XM to distribute books to 3 readers:
1: 1,2,3 2: 1,2,4 3: 1,2,5 4: 1,3,2 5: 1,3,4
6: 1,3,5 7: 1,4,2 8: 1,4,3 9: 1,4,5 10:1,5,2
11:1,5,3 12:1,5,4 13:2,1,3 14:2,1,4 15:2,1,5
16:2,3,1 17:2,3,4 18:2,3,5 19:2,4,1 20:2,4,3
21:2,4,5 22:2,5,1 23:2,5,3 24:2,5,4 25:3,1,2
26:3,1,4 27:3,1,5 28:3,2,1 29:3,2,4 30:3,2,5
31:3,4,1 32:3,4,2 33:3,4,5 34:3,5,1 35:3,5,2
36:3,5,4 37:4,1,2 38:4,1,3 39:4,1,5 40:4,2,1
41:4,2,3 42:4,2,5 43:4,3,1 44:4,3,2 45:4,3,5
46:4,5,1 47:4,5,2 48:4,5,3 49:5,1,2 50:5,1,3
51:5,1,4 52:5,2,1 53:5,2,3 54:5,2,4 55:5,3,1
56:5,3,2 57:5,3,4 58:5,4,1 59:5,4,2 60:5,4,3
no9.杨辉三角形
在屏幕上显示杨辉三角形
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
......................................
*问题分析与算法设计
杨辉三角形中的数,正是(x+y)的N次方幂展开式各项的系数。本题作为程序设计中具有代表性的题目,求解的方法很多,这里仅给出一种。
从杨辉三角形的特点出发,可以总结出:
1)第N行有N+1个值(设起始行为第0行)
2)对于第N行的第J个值:(N>=2)
当J=1或J=N+1时:其值为1
J!=1且J!=N+1时:其值为第N-1行的第J-1个值与第N-1行第J个值之和
将这些特点提炼成数学公式可表示为:
1 x=1或x=N+1
c(x,y)=
c(x-1,y-1)+c(x-1,y) 其它
本程序应是根据以上递归的数学表达式编制的。
*程序说明与注释
#include<stdio.h>
void main()
{
int i,j,n=13;
printf("N=");
while(n>12)
scanf("%d",&n);
for(i=0;i<=n;i++)
{
for(j-0;j<24-2*i;j++) printf(" ");
for(j=1;j<i+2;j++) printf("%4d",c(i,j));
printf("\\n");
}
}
void int c(int x,int y)
{
int z;
if((y==1)||(y==x+1)) return 1;
z=c(x-1,y-1)+c(x-1,y);
return z;
}
no10.数制转换
将任一整数转换为二进制形式
*问题分析与算法设计
将十进制整数转换为二进制的方法很多,这里介绍的实现方法利用了C语言能够对位进行操作的特点。对于C语言来说,一个整数在计算机内就是以二进制的形式存储的,所以没有必要再将一个整数经过一系列的运算转换为二进制形式,只要将整数在内存中的二进制表示输出即可。
*程序说明与注释
#include<stdio.h>
void printb(int,int);
void main()
{
int x;printf("Input number:");
scanf("%d",&x);
printf("number of decimal form:%d\\n",x);
printf(" it\'s binary form:");
printb(x,sizeof(int)*8);
putchar(\'\\n\');
}
void printb(int x,int n)
{
if(n>0)
{
putchar(\'0\'+((unsigned)(x&(1<<(n-1)))>>(n-1)));
printb(x,n-1);
}
}
*运行结果
输入:8
输出:
number of decimal form:8
it\'s bunary form:0000000000001000
输入:-8
输出:number of decimal form:-8
it\'s binary form:11xxxxxxxxxxxx0
输入:32767
输出:number of decimal form:32767
it\'s binary form:011xxxxxxxxxxxx
输入:-32768
输出:number of decimal form:-32768
it\'s binary form:1000000000000000
输入:128
输出:number of decimal form:128
it\'s binary form:0000000010000000
no11.打鱼还是晒网
中国有句俗语叫“三天打鱼两天晒网”。某人从19xx年1月1日起开始“三天打鱼两天晒网”,问这个人在以后的某一天中是“打鱼”还是“晒网”。
*问题分析与算法设计
根据题意可以将解题过程分为三步:
1)计算从19xx年1月1日开始至指定日期共有多少天;
2)由于“打鱼”和“晒网”的周期为5天,所以将计算出的天数用5去除;
3)根据余数判断他是在“打鱼”还是在“晒网”;
若 余数为1,2,3,则他是在“打鱼”
否则 是在“晒网”
在这三步中,关键是第一步。求从19xx年1月1日至指定日期有多少天,要判断经历年份中是否有闰年,二月为29天,平年为28天。闰年的方法可以用伪语句描述如下:
如果 ((年能被4除尽 且 不能被100除尽)或能被400除尽) 则 该年是闰年;
否则 不是闰年。
C语言中判断能否整除可以使用求余运算(即求模)
*程序与程序注释
#include<stdio.h>
int days(struct date day);
struct date{
int year;
int month;
int day;
};
void main()
{
struct date today,term;
int yearday,year,day;
printf("Enter year/month/day:");
scanf("%d%d%d",&today.year,&today.month,&today.day); term.month=12;
term.day=31;
for(yearday=0,year=1990;year<today.year;year++) {
term.year=year;
yearday+=days(term);
}
yearday+=days(today);
day=yearday%5;
if(day>0&&day<4) printf("he was fishing at that day.\\n"); else printf("He was sleeping at that day.\\n");
}
int days(struct date day)
{
static int day_tab[2][13]=
{{0,31,28,31,30,31,30,31,31,30,31,30,31,}, {0,31,29,31,30,31,30,31,31,30,31,30,31,},
};
int i,lp;
lp=day.year%4==0&&day.year%100!=0||day.year%400==0;
for(i=1;i<day.month;i++)
day.day+=day_tab[lp];
return day.day;
}
*运行结果
Enter year/month/day:1991 10 25
He was fishing at day.
Enter year/month/day:1992 10 25
He was sleeping at day.
Enter year/month/day:1993 10 25
He was sleeping at day
--------------------------------------------------------------------------------
no12.抓交通肇事犯
一辆卡车违反交通规则,撞人后逃跑。现场有三人目击事件,但都没有记住车号,只记下车号的一些特征。甲说:牌照的前两位数字是相同的;乙说:牌照的后两位数字是相同的,但与前两位不同;丙是数学家,他说:四位的车号刚好是一个整数的平方。请根据以上线索求出车号。
*问题分析与算法设计
按照题目的要求造出一个前两位数相同、后两位数相同且相互间又不同的整数,然后判断该整数是否是另一个整数的平方。
*程序与程序注释
#include<stdio.h>
#include<math.h>
void main()
{
int i,j,k,c;
for(i=1;i<=9;i++)
for(j=0;j<=9;j++)
if(i!=j)
{
k=i*1000+i*100+j*10+j;
for(c=31;c*c<k;c++);
if(c*c==k) printf("Lorry--No. is %d.\\n",k);
}
}
*运行结果
Lorry _No.is 7744
no13.该存多少钱
假设银行一年整存零取的月息为0.63%。现在某人手中有一笔钱,他打算在今后的五年中的年底取出1000元,到第五年时刚好取完,请算出他存钱时应存入多少。
*问题分析与算法设计
分析存钱和取钱的过程,可以采用倒推的方法。若第五年年底连本带息要取1000元,则要先求出第五年年初银行存款的钱数:
第五年初存款=1000/(1+12*0.0063)
依次类推可以求出第四年、第三年......的年初银行存款的钱数:
第四年年初存款=(第五年年初存款+1000)/(1+12*0.0063)
第三年年初存款=(第四年年初存款+1000)/(1+12*0.0063)
第二年年初存款=(第三年年初存款+1000)/(1+12*0.0063)
第一年年初存款=(第二年年初存款+1000)/(1+12*0.0063)
通过以上过程就可以很容易地求出第一年年初要存入多少钱。
*程序与程序注释
#include<stdio.h>
void main()
{
int i;
float total=0;
for(i=0;i<5;i++)
total=(total+1000)/(1+0.0063*12);
printf("He must save %.2f at first.\\n",total);
}
*运行结果
He must save 4039.44 at first
14.怎样存钱利最大
假设银行整存整取存款不同期限的月息利率分别为:
0.63% 期限=1年
0.66% 期限=2年
0.69% 期限=3年
0.75% 期限=5年
0.84% 期限=8年
利息=本金*月息利率*12*存款年限。
现在某人手中有2000元钱,请通过计算选择一种存钱方案,使得钱存入银行20年后得到的利息最多(假定银行对超过存款期限的那一部分时间不付利息)。
*问题分析与算法
为了得到最多的利息,存入银行的钱应在到期时马上取出来,然后立刻将原来的本金和利息加起来再作为新的本金存入银行,这样不断地滚动直到满20年为止,由于存款的利率不同,所以不同的存款方法(年限)存20年得到的利息是不一样的。
分析题意,设2000元存20年,其中1年存i1次,2年存i2次,3年存i3次,5年存i5次,8年存i8次,则到期时存款人应得到的本利合计为:
2000*(1+rate1)i1*(1+rate2)i2*(1+rate3)i3*(1+rate5)i5*(1+rate8)i8
其中rateN为对应存款年限的利率。根据题意还可得到以下限制条件:
0<=i8<=2
0<=i5<=(20-8*i8)/5
0<=i3<=(20-8*i8-5*i5)/3
0<=i2<=(20-8*i8-5*i5-3*i3)/2
0<=i1=20-8*i8-5*i5-3*i3-2*i2
可以用穷举法穷举所有的i8、i5、i3、i2和i1的组合,代入求本利的公式计算出最大值,就是最佳存款方案。
*程序与程序注释
#include<stdio.h>
#include<math.h>
void main()
{
int i8,i5,i3,i2,i1,n8,n5,n3,n2,n1;
float max=0,term;
for(i8=0;i8<3;i8++)
for(i5=0;i5<=(20-8*i8)/5;i5++)
for(i3=0;i3<=(20-8*i8-5*i5)/3;i3++)
for(i2=0;i2<=(20-8*i8-5*i5-3*i3)/2;i2++)
{
i1=20-8*i8-5*i5-3*i3-2*i2;
term=2000.0*pow((double)(1+0.0063*12),(double)i1) *pow((double)(1+2*0.0063*12),(double)i2) *pow((double)(1+3*0.0069*12),(double)i3) *pow((double)(1+5*0.0075*12),(double)i5) *pow((double)(1+8*0.0084*12),(double)i8);
if(term>max)
{
max=term;n1=i1;n2=i2;n3=i3;n5=i5;n8=i8;
}
}
printf("For maxinum profit,he should so save his money in a bank:\\n"); printf(" made fixed deposit for 8 year: %d times\\n",n8);
printf(" made fixed deposit for 5 year: %d times\\n",n5);
printf(" made fixed deposit for 3 year: %d times\\n",n3);
printf(" made fixed deposit for 2 year: %d times\\n",n2);
printf(" made fixed deposit for 1 year: %d times\\n",n1);
printf(" Toal: %.2f\\n",max);
}
*运行结果
For maxinum profit,he should so save his money in a bank:
made fixed deposit for 8 year: 0times
made fixed deposit for 5 year: 4times
made fixed deposit for 3 year: 0times
made fixed deposit for 2 year: 0times
made fixed deposit for 1 year: 0times
Total:8841.01
可见最佳的存款方案为连续四次存5年期。
*思考题
某单位对职工出售住房,每套为2万元。买房付款的方法是:
一次交清,优惠20%
从第一年开始,每年年初分期付款:
5年交清,优惠50%;
10年交清,优惠10%;
20年交清,没有优惠。
现在有人手中正好有2万元,若假定在今后20年中物价和银行利率均保持不变,问他应当选择哪种付款方式可以使应付的钱最少?
--------------------------------------------------------------------------------
no15.捕鱼和分鱼
A、B、C、D、E五个人在某天夜里合伙去捕鱼,到第二天凌晨时都疲惫不堪,于是各自找地方睡觉。日上三杆,A第一个醒来,他将鱼分为五份,把多余的一条鱼扔掉,拿走自己的一份。B第二个醒来,也将鱼分为五份,把多余的一条鱼扔掉,保持走自己的一份。C、D、E依次醒来,也按同样的方法拿走鱼。问他们合伙至少捕了多少条鱼?
*问题分析与算法设计
根据题意,总计将所有的鱼进行了五次平均分配,每次分配时的策略是相同的,即扔掉一条鱼后剩下的鱼正好分成五份,然后拿走自己的一份,余下其它的四份。
假定鱼的总数为X,则X可以按照题目的要求进行五次分配:X-1后可被5整除,余下的鱼为4*(X-1)、
5。若X满足上述要求,则X就是题目的解。
*程序与程序注释
#include<stdio.h>
void main()
{
int n,i,x,flag=1;
for(n=6;flag;n++)
{
for(x=n,i=1&&flag;i<=5;i++)
if((x-1)%5==0) x=4*(x-1)/5;
else flag=0;
if(flag) break;
else flag=1;
}
printf("Total number of fish catched=%d\\n",n);
}
*运行结果
Total number of fish catched = 3121
*问题的进一步讨论
程序采用试探法,试探的初值为6,每次试探的步长为1。这是过分保守的做法。可以在进一步分析题目的基础上修改此值,增大试探的步长值,以减少试探次数。
*思考题
请使用其它的方法求解本题
16.出售金鱼
买卖提将养的一缸金鱼分五次出售系统上一次卖出全部的一半加二分之一条;第二次卖出余下的三分之一加三分之一条;第三次卖出余下的四分之一加四分之一条;第四次卖出余下的五分之一加五分之一条;最后卖出余下的11条。问原来的鱼缸中共有几条金鱼?
*题目分析与算法设计
题目中所有的鱼是分五次出售的,每次卖出的策略相同;第j次卖剩下的(j+1)分之一再加1/(j+1)条。第五次将第四次余下的11条全卖了。
假定第j次鱼的总数为X,则第j次留下:
x-(x+1)/(j+1)
当第四次出售完毕时,应该剩下11条。若X满足上述要求,则X就是题目的解。
应当注意的是:"(x+1)/(j+1)"应满足整除条件。试探X的初值可以从23开始,试探的步长为2,因为X的值一定为奇数。
*程序说明与注释
#include<stdio.h>
void main()
{
int i,j,n=0,x;
for(i=23;n==0;i+=2)
{
for(j=1,x=i;j<=4&&x>=11;j++)
if((x+1)%(j+1)==0)
x-=(x+1)/(j+1);
else {x=0;break;}
if(j==5&&x==11)
{
printf("There are %d fishes at first.\\n",i);
n=1;
}
}
}
*运行结果
There are 59 fishes at first.
*思考题
日本著名数学游戏专家中村义作教授提出这样一个问题:父亲将2520个桔子分给六个儿子。分完后父亲说:“老大将分给你的桔子的1/8给老二;老二拿到后连同原先的桔子分1/7给老三;老三拿到后连同原先的桔子分1/6给老四;老四拿到后连同原先的桔子分1/5给老五;老五拿到后连同原先的桔子分1/4给老六;老六拿到后连同原先的桔子分1/3给老大”。结果大家手中的桔子正好一样多。问六兄弟原来手中各有多少桔子?
no17 分数四则运算
对输入的两个分数进行+、-、*、/四则运算,输出分数结果。
算法分析如下:
对分数b/a与d/c,不管哪一种运算,其运算结果均为y/x形式。对结果y/x进行化简,约去分子分母的公因数:试用i(i=1,...,y)对y,x进行试商,若能同时整除y,x,则y,x同时约去公因数i,最后打印约简的分数。
程序代码如下:
#include<stdio.h>
void main()
{
long int a,b,c,d,i,x,y,z;
char op;
printf("两分数b/a,d/c作+,-,*,/四则运算,结果为分数。\\n");
printf("请输入分数运算式。\\n");
scanf("%ld/%ld%c%ld/%ld",&b,&a,&op,&d,&c);
if(a==0||c==0) {printf("分母为0输入错误!");exit(0);}
if(op==\'+\'){y=b*c+d*a;x=a*c;}
if(op==\'-\'){y=b*c-d*a,x=a*c;}
if(op==\'*\'){y=b*d;x=a*c;}
if(op==\'/\'){y=b/c;x=a/d;}
z=x;
if(x>y) z=y;
i=z;
while(i>1)
{
if(x%i==0&&y%i==0){x=x/i;y=y/i;continue;}
i--;
}
printf("%ld/%ld%c%ld/%ld=%ld/%ld.\\n",b,a,op,d,c,y,x);
}
--------------------------------------------------------------------------------
no18.平分七筐鱼
甲、乙、丙三位鱼夫出海打鱼,他们随船带了21只箩筐。当晚返航时,他们发现有七筐装满了鱼,还有七筐装了半筐鱼,另外七筐则是空的,由于他们没有秤,只好通过目测认为七个满筐鱼的重量是相等的,7个半筐鱼的重量是相等的。在不将鱼倒出来的前提下,怎样将鱼和筐平分为三份?
*问题分析与算法设计
根据题意可以知道:每个人应分得七个箩筐,其中有3.5筐鱼。采用一个3*3的数组a来表示三个人分到的东西。其中每个人对应数组a的一行,数组的第0列放分到的鱼的整筐数,数组的第1列放分到的半筐数,数组的第2列放分到的空筐数。由题目可以推出:
。数组的每行或每列的元素之和都为7;
。对数组的行来说,满筐数加半筐数=3.5;
。每个人所得的满筐数不能超过3筐;
。每个人都必须至少有1 个半筐,且半筐数一定为奇数
对于找到的某种分鱼方案,三个人谁拿哪一份都是相同的,为了避免出现重复的分配方案,可以规定:第二个人的满筐数等于第一个人的满筐数;第二个人的半筐数大于等于第一个人的半筐数。
*程序与程序注释
#include<stdio.h>
int a[3][3],count;
void main()
{
int i,j,k,m,n,flag;
printf("It exists possible distribtion plans:\\n");
for(i=0;i<=3;i++)
{
a[0][0]=i;
for(j=i;j<=7-i&&j<=3;j++)
{
a[1][0]=j;
if((a[2][0]=7-j-a[0][0])>3)continue;
if(a[2][0]<a[1][0])break;
for(k=1;k<=5;k+=2)
{
a[0][1]=k;
for(m=1;m<7-k;m+=2)
{
a[1][1]=m;
a[2][1]=7-k-m;
for(flag=1,n=0;flag&&n<3;n++)
if(a[n][0]+a[n][1]<7&&a[n][0]*2+a[n][1]==7)
a[n][2]=7-a[n][0]-a[n][1];
else flag=0;
if(flag)
{
printf("No.%d Full basket Semi--basket Empty\\n",++count);
for(n=0;n<3;n++)
printf(" fisher %c: %d %d %d\\n",
\'A\'+n,a[n][0],a[n][1],a[n][2]);
}
}
}
}
}
}
* 运行结果
It exists possible distribution plans:
No.1 Full basket Semi--basket Empty
fisher A: 1 5 1
fisher B: 3 1 3
fisher C: 3 1 3
No.2 Full basket Semi--basket Empty
fisher A: 2 3 2
fisher B: 2 3 2
fisher C: 3 1 3
*思考题
晏会上数学家出了一道难题:假定桌子上有三瓶啤酒,癣瓶子中的酒分给几个人喝,但喝各瓶酒的人数是不一样的。不过其中有一个人喝了每一瓶中的酒,且加起来刚好是一瓶,请问喝这三瓶酒的各有多少人? (答案:喝三瓶酒的人数分别是2人、3人和6人)
no19.有限5位数
个位数为6且能被3整除的五位数共有多少?
*题目分析与算法设计
根据题意可知,满足条件的五位数的选择范围是10006、10016。。。99996。可设基础数i=1000,通过计算i*10+6即可得到欲选的数(i的变化范围是1000~999),再判断该数能否被3整除。 *程序说明与注释
#include<stdio.h>
void main()
{
long int i;
int count=0;
for(i=1000;i<9999;i++)
if(!((i*10+6)%3))
count++;
printf("count=%d\\n",count);
}
*运行结果
count=2999
*思考题
求100到1000之间有多少个其数字之和为5的整数。
(答案:104,113,122,131,140,203,212,221,230,302,311,320,401,410,500)
no20. 除不尽的数
一个自然数被8除余1,所得的商被8除也余1,再将第二次的商被8除后余7,最后得到一个商为a。又知这个自然数被17除余4,所得的商被17除余15,最后得到一个商是a的2倍。求这个自然数。 *题目分析与算法设计
根据题意,可设最后的商为i(i从0开始取值),用逆推法可以列出关系式:
(((i*8+7)*8)+1)*8+1=((2*i*17)+15)*18+4
再用试探法求出商i的值。
*程序说明与注释
#include<stdio.h>
void main()
{
int i;
for(i=0;;i++)
if(((i*8+7)*8+1)*8+1==(34*i+15)*17+4)
{
printf("The required number is: %d\\n",(34*i+15)*17+4);
break;
}
}
*运行结果
The required number is:199320.一个奇异的三位数
一个自然数的七进制表达式是一个三位数,而这个自然数的九进制表示也是一个三位数,且这两个三位数的数码正好相反,求这个三位数。
*题目分析与算法设计
根据题意可知,七进制和九进制表示的这全自然数的每一位一定小于7,可设其七进制数形式为kji(i、j、k的取值分别为1~6),然后设其九进制表示形式为ijk。
*程序说明与注释
#include<stdio.h>
void main()
{
int i,j,k;
for(i=1;i<7;i++)
for(j=0;j<7;j++)
for(k=1;k<7;k++)
if(i*9*9+j*9+k==i+j*7+k*7*7)
{
printf("The special number with 3 digits is:");
printf("%d%d%d(7)=%d%d%d(9)=%d(10)\\n",k,j,i,i,j,k,i*9*9+j*9+k); }
}
*运行结果
The special number with 3 digits is:503(7)=305(9)=248(10)
